题目传送门
题目大意:
在一个平面直角坐标系上,给定 \(n\) 个点的坐标 \((x,y)\),\(m\) 次询问,每次询问一个矩形范围内的点的数量,此矩形用 \(\{a, b, c, d\}\) 来描述,其中 \((a, b)\) 为左下角,\((c, d)\) 为右上角。
思路:
不难将题目转化为:给定一个长度为 \(n\) 的序列,序列中的每个元素都有两个属性 \(x,y\),每次询问求 \(x\in [a, c]\) 且 \(y\in [b, d]\) 的元素个数。
和 这道题 差不多的思路,都用类似前缀和的思想,但这道题是二维前缀和。
对于一个询问,我们要处理的其实是这样一个图形:
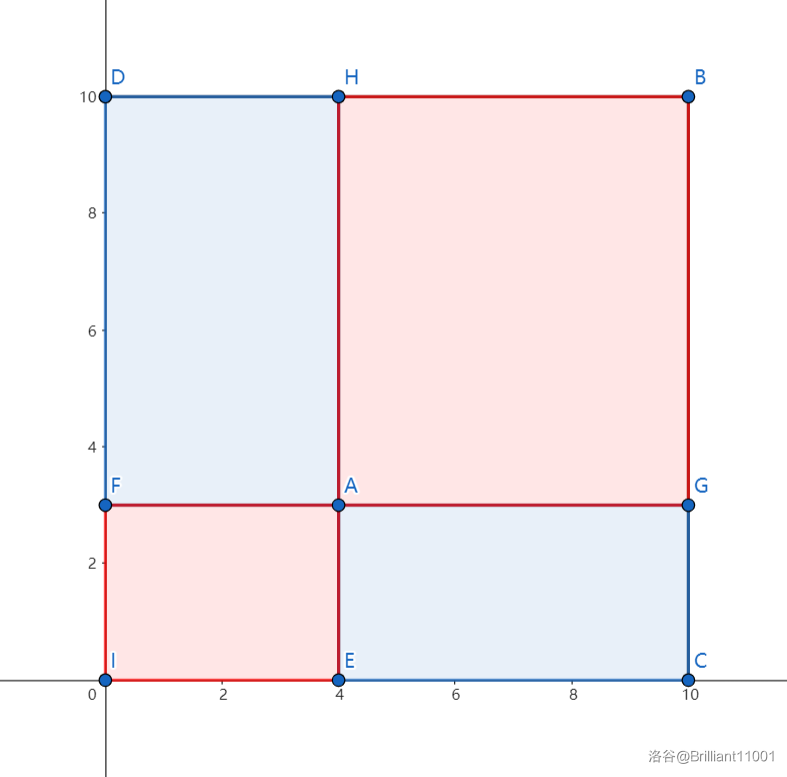
其中四边形 \(\text{AGBH}\) 是我们要求的。
设此询问为 \(\{x1, y1, x2, y2\}\)
\(A(x1 - 1, y1 - 1)\)
\(E(x1 - 1, y2)\)
\(G(x2, y1 - 1)\)
\(B(x2, y2)\)
设左下角为 \((0, 0)\),右上角为 \((i, j)\) 的矩形中点的数量为 \(sum_{i, j}\)。
所以我们要求的是 \(sum_{x2, y2} + sum_{x1 - 1, y1 - 1} - sum_{x1 - 1, y2} - sum_{x2, y1 - 1}\)。
将询问分成四个部分,分别存 \(A,E,G,B\) 四个,然后将给定的点和询问都按照 \(x\) 升序排列,这样 \(x\) 的限制就可以不用管了,再建立一个树状数组来维护 \(y\) 即可。
需要注意的几个点:
- 本题值域较大,需要离散化;(其实也没有那么大,不离散化也能过)
- 离散化后的数要从 \(1\) 开始,因为为 \(0\) 的话树状数组会死循环;
- 询问要分成 \(4\) 份,也就是说要开 \(4\) 倍空间,同理,树状数组的值域也要开大点。
\(\texttt{Code:}\)
#include <vector>
#include <iostream>
#include <algorithm>
#define lowbit(x) x & -x
using namespace std;
const int N = 500010, M = 20000010;
int n, m;
struct BIT{
int c[M];
void add(int x, int y) {
for(; x < M; x += lowbit(x)) c[x] += y;
}
int ask(int x) {
int res = 0;
for(; x; x -= lowbit(x)) res += c[x];
return res;
}
}tr;
vector<int> nums;
struct node{
int id, x, y, sign;
bool operator< (const node &o) const {
return x < o.x;
}
}q[N << 2];
int tt;
struct Point{
int x, y;
bool operator< (const Point &o) const {
return x < o.x;
}
}a[N];
int ans[N];
int find(int x) {
return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}
int main() {
scanf("%d%d", &n, &m);
int x, y;
for(int i = 1; i <= n; i++) {
scanf("%d%d", &x, &y);
a[i] = {x, y};
nums.push_back(y);
}
int x1, y1, x2, y2;
for(int i = 1; i <= m; i++) {
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
q[++tt] = {i, x1 - 1, y1 - 1, 1};
q[++tt] = {i, x1 - 1, y2, -1};
q[++tt] = {i, x2, y1 - 1, -1};
q[++tt] = {i, x2, y2, 1};
nums.push_back(y1 - 1), nums.push_back(y2);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
sort(a + 1, a + n + 1);
sort(q + 1, q + tt + 1);
int id = 1;
for(int i = 1; i <= tt; i++) {
while(a[id].x <= q[i].x && id <= n) tr.add(find(a[id++].y), 1);
ans[q[i].id] += q[i].sign * tr.ask(find(q[i].y));
}
for(int i = 1; i <= m; i++)
printf("%d\n", ans[i]);
return 0;
}