二分图
定义:
二分图是一种特殊的图,顶点被分为左右两部分,且两部分内没有连边。
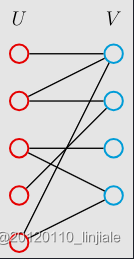
- 来源于oiwiki
因为此图可以被分为两个集合,所以每条边链接的两个顶点都可以看作一个黑色,一个白色(如上图)。
判定是否为二分图
- 需要判断是否能分为两个集合
可以用染色法。
用深搜去遍历图,给每个顶点赋上颜色(黑白),若出现自相矛盾的情况(一条边俩顶点颜色一致),则不是。
二分图最大匹配
给定一个二分图 $G$,分左右两部分,各部分之间的点没有边连接,要求选出一些边,使得这些边没有公共顶点,且边的数量最大。
- 匈牙利算法(增广路算法)
利用贪心的思想,枚举左边的每个点,看看能否匹配到右边的点。
1、设 $s\in \emptyset$,即所有边都为未匹配边。
2、寻找增广路,把路径上的所有边匹配状态取反,取到一个更大的匹配 $S'$。
3、重复第 $2$ 步,直到图中不存在增广路。
寻找增广路
匈牙利算法依次尝试给每一个左边节点 $x$ 匹配一个右边节点 $y$,若匹配成功,则需要满足以下条件之一:
1、$y$ 本来就是未匹配点。此时 $(x,y)$ 本身就是非匹配边,自己构成一条长度为 $1$ 的增广路。
2、$y$ 已与左部节点 $x'$ 配对,但从 $x'$ 可以再次找到一个右边节点 $y'$ 配对,则 $(x,y,x',y')$ 构成一条增广路。
P3386 【模板】二分图最大匹配
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,e;
int u,v;
const int MAXN=1005,MAXE=1e4+5;
int head[MAXN],cnt_edge;
bool g[MAXN][MAXN];
int ans;
bool vis[MAXN];
int match[MAXN];
bool dfs(int now)
{
for(int i=1;i<=m;i++)
{
if(!vis[i]&&g[now][i])
{
vis[i]=true;
if(!match[i]||dfs(match[i]))
{
match[i]=now;
return true;
}
}
}
return false;
}
int main(){
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=e;i++)
{
scanf("%d%d",&u,&v);
g[u][v]=true;
}
for(int i=1;i<=n;i++)
{
memset(vis,false,sizeof(vis));
if(dfs(i)) ans++;
}
printf("%d\n",ans);
return 0;
}