线段树

把给定的区间转换成如图所示的一棵二叉树

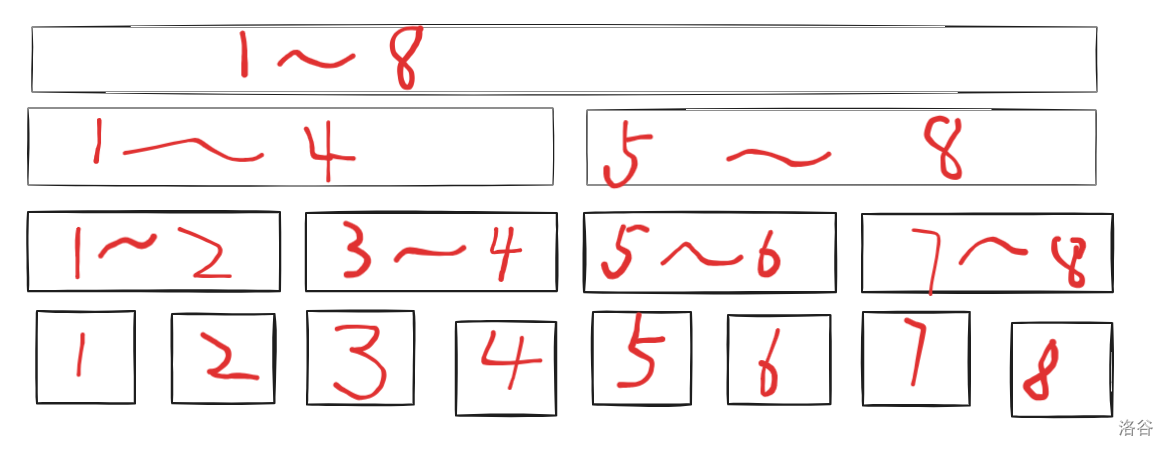
每次把区间一分为 2, 左边是左儿子, 右边是右儿子

对于每个节点的信息, 都可以由两个儿子的信息得到

如何单点查询/修改

可以发现, 两个儿子处理的区间没有交集, 所以每次只要判断是在左儿子还是在右儿子, 不断的递归

对于区间查询, 每一次记录修改后的答案, 如果查询区间完全包含找到的节点, 直接返回答案

时间复杂度

我们先把所以节点放到最下面一层, 一次往上合并, 我们发现, 查询的区间如果在同一层一定是连续的, 而且如果有一层有 3 个节点, 其中一定有两个可以合并到上一层, 又最多只有 \(\lceil \log_2 \rceil\) 层

对于区间修改, 我们要用到懒标记, 如果修改区间完全包含这个区间, 给节点打上一个标记, 每次要用到时再下传, 时间复杂度与上面类似

时间复杂度 \(O(n \log n)\)
空间复杂度 \(O(n)\)

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

using LL = long long;

LL n, m, a[N], l, r, k, op;

struct TREE{
  struct Node{
    LL l, r, dat, flag = 0;
  }t[4 * N];
  void dfs(LL p, LL l, LL r){
    t[p].l = l, t[p].r = r;
    if(l == r){
      t[p].dat = a[l];
      return;
    }
    LL mid = (l + r) >> 1;
    dfs(p * 2, l, mid);
    dfs(p * 2 + 1, mid + 1, r);
    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
  }
  void DFS(LL p, LL l, LL r, LL k){
    if(l <= t[p].l && r >= t[p].r){
      t[p].dat += (t[p].r - t[p].l + 1) * k, t[p].flag += k;
      return;
    }
    if(t[p].flag){
      t[p * 2].dat += (t[p * 2].r - t[p * 2].l + 1) * t[p].flag;
      t[p * 2 + 1].dat += (t[p * 2 + 1].r - t[p * 2 + 1].l + 1) * t[p].flag;
      t[p * 2].flag += t[p].flag, t[p * 2 + 1].flag += t[p].flag;
      t[p].flag = 0;
    }
    int mid = (t[p].l + t[p].r) >> 1;
    if(l <= mid){
      DFS(p * 2, l, r, k);
    }
    if(r > mid){
      DFS(p * 2 + 1, l, r, k);
    }
    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
  }
  LL SUM(LL p, LL l, LL r){
    if(l <= t[p].l && r >= t[p].r){
      return t[p].dat;
    }
    if(t[p].flag){
      t[p * 2].dat += (t[p * 2].r - t[p * 2].l + 1) * t[p].flag;
      t[p * 2 + 1].dat += (t[p * 2 + 1].r - t[p * 2 + 1].l + 1) * t[p].flag;
      t[p * 2].flag += t[p].flag, t[p * 2 + 1].flag += t[p].flag;
      t[p].flag = 0;
    }
    LL sum = 0;
    int mid = (t[p].l + t[p].r) >> 1;
    if(l <= mid){
      sum += SUM(p * 2, l, r);
    }
    if(r > mid){
      sum += SUM(p * 2 + 1, l, r);
    }
    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
    return sum;
  }
}tree;

int main(){
  cin >> n >> m;
  for(LL i = 1; i <= n; ++i){
    cin >> a[i];
  }
  tree.dfs(1, 1, n);
  for(LL i = 1; i <= m; ++i){
    cin >> op;
    if(op == 1){
      cin >> l >> r >> k;
      tree.DFS(1, l, r, k);
    }
    else{
      cin >> l >> r;
      cout << tree.SUM(1, l, r) << '\n';
    }
  }
  return 0;
}