前言
线段树用于维护区间上的值,可以在 $O(\log n)$ 的时间复杂度内实现单点,区间修改及查询。并且所有满足结合律的运算都可以用线段树进行加速。
基本操作
建树
给你长度为 $n$ 的正整数序列 $A$,要你实现单点修改与区间查询。(加和)
这就是线段树的基本题目。线段树,字面上来看就是把线段映射到树上,可以想到每个节点代表一个区间。
那么我们可以把每个区间分成两半,作为节点的左右子节点。
最常见的树左右子节点就是 $rt \times 2$ 和 $rt \times 2 + 1$(堆式存储)。可以直接开 $4$ 倍空间。
可以知道,如果有 $n$ 个叶子节点,最大值是 $2 ^ {\lfloor \log n \rfloor + 1}$ 的。当 $n = 2^x + 1$ 时,$\dfrac{2 ^ {\lfloor \log n \rfloor + 1}}{n}$ 取得最大值 $4n - 5$。
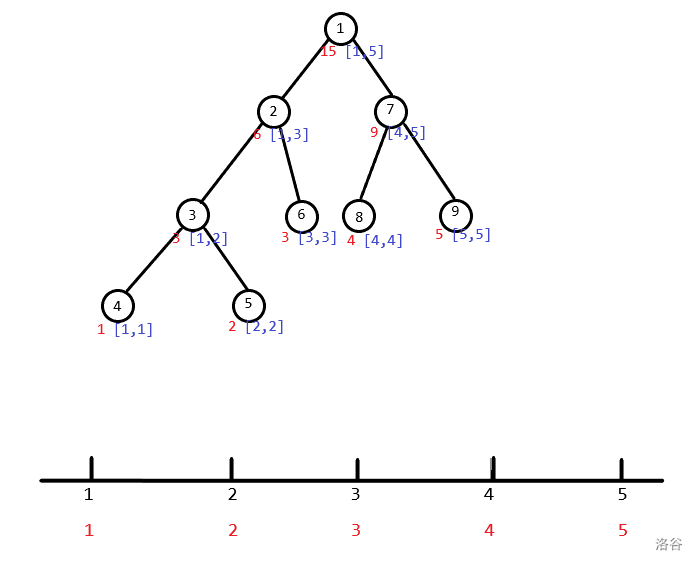
如图就是 $n = 5, A = {1, 2, 3, 4, 5}$ 时的线段树(加和)。
我们可以发现,对于每个区间 $[x,y]$,都被分成了 $[x, \lfloor \dfrac{x + y}{2} \rfloor]$ 和 $[\lfloor \dfrac{x + y}{2} \rfloor + 1, y]$ 这两个区间。如果我们令根节点的深度为 $0$,那么可以发现整棵树的深度不超过 $\log n + 1$,这也就意味着我们至多经过 $\log n$ 条边就可以找到一个区间。
建树时我们可以递归建树,如果 $l = r$,也就意味着到了单点,这时直接赋值。返回时再更新节点值即可。
void pushup (int node) { tree[node] = tree[node << 1] + tree[(node << 1) + 1]; }
void build (int node, int l, int r){
if (l == r){
tree[node] = ta[l];
return ;
}
int mid = l + ((r - l) >> 1);
build ((node << 1), l, mid);
build ((node << 1) + 1, mid + 1, r);
pushup (node);
}
因为深度不超过 $\log n +1$,所以复杂度应该是 $O(\log n)$ 的。
单点修改
当我们单点修改时,只需要想建树那样遍历,如果遍历到单点就直接修改,然后返回,更新。
void modify (int node, int l, int r, int a, int c){
if (l == r){
tree[node] = c;
return ;
}
int mid = l + ((r - l) >> 1);
if (a <= mid) modify ((node << 1), l, mid, a, b);
else modify ((node << 1) + 1, mid + 1, r, a, b);
pushup (node);
}
区间查询
单点查询很好做,关键就是区间查询。
对于查询区间,我们一定可以把它分成几个序列上的区间,对应树上的节点。关键就是这些节点。
设当前遍历到的区间为 $[l,r]$,要查询的区间为 $[s,t]$。
如果要查询的区间在左边,可以发现一定是 $s \le \lfloor \dfrac{x + y}{2} \rfloor$;如果在右边,那么一定是 $t \gt \lfloor \dfrac{x + y}{2} \rfloor$。没有等于的情况是因为向下取整,如果等于就已经被左边的区间包含了,不能算重,所以没有等于。
那么把左右区间累加起来,就是这个区间的贡献,直接返回即可。
long long query (int node, int l, int r, int s, int t) {
if (s <= l && r <= t) return tree[node];
int mid = l + ((r - l) >> 1);
long long ret = 0;
if (s <= mid) ret += query (node << 1, l, mid, s, t);
if (t > mid) ret += query ((node << 1) + 1, mid + 1, r, s, t);
return ret;
}
至此,基本的,没有任何其他东西的一个纯粹的线段树我们就打完了。可以发现每个操作都是基于线段树的层数来定的复杂度,所以都是 $O(\log n)$ 的。
但是拓展操作远远不止于此,上题!
区间修改
你长度为 $n$ 的正整数序列 $A$,要你实现区间修改与区间查询。
这题唯一的不同就在于区间修改。如果每个暴力单点修改的话,复杂度 $O(n \log n)$,会爆炸。
这时就要引入一种叫懒惰标记的东西。
还是遍历,当这个区间在查询区间中,我们就先修改它的值,给它挂上懒惰标记,但不修改它子节点的值。
你可能已经想到了,再一次遍历的时候就可以下传懒惰标记,以达到区间修改的目的。
void pushdown (int node, int l, int r) {
int ls = node << 1, rs = (node << 1) + 1, mid = l + ((r - l) >> 1);
if (lazy[node]) {
int x = lazy[node];
tree[ls] += (mid - l + 1) * x; tree[rs] += (r - mid) * x;
lazy[ls] += x; lazy[rs] += x;
lazy[node] = 0;
}
}
void modify (int node, int l, int r, int s, int t, long long c) {
if (s <= l && r <= t) {
tree[node] += (r - l + 1) * c;
lazy[node] += c;
return ;
}
int mid = l + ((r - l) >> 1);
pushdown (node, l, r);
if (s <= mid) modify (node << 1, l, mid, s, t, c);
if (t > mid) modify ((node << 1) + 1, mid + 1, r, s, t, c);
pushup (node);
}
动态开点线段树
线段树的时间复杂度虽然小,但是空间复杂度大,有 $4n$,如何来优化呢?
我们可以把懒惰标记的思想用在节点上面,就成了动态开点。也就是访问到这个节点时再创建这个节点,但不能用 $rt \times 2$ 这种来存储了,必须另外专门存储。
就拿单点修改来举例吧。
int n, tot, rt;
int tree[N << 1], ls[N << 1], rs[N << 1];
void modify (int &node, int l, int r, int s, int c) {
if (!node) node = ++tot;
if (l == r) {
tree[node] = c;
return ;
}
int mid = l + ((r - l) >> 1);
if (s <= mid) modify (ls[node], l, mid, s, c);
else modify (rs[node], mid + 1, r, s, c);
pushup (node);
}
小清新线段树
上题。
给你一个长度为 $n$ 的正整数序列 $A$,要实现区间开方与区间求和。
注意到,区间开方是从未有过的操作,只能一个一个单点修改,复杂度肯定爆炸。
但是 $\sqrt 1 = 1,\sqrt 0 = 0$,我们可以另存一个最大值。如果这个区间的最大值小于等于 $1$ 的话,就不用修改了。
数列里的数不超过 $10^{12}$。
$$\sqrt{10^{12}} = 10^6 \to \sqrt{10^6} = 1000 \to \sqrt{1000} \approx 31.62 \to \sqrt{31.62} \approx 5.62 \to \sqrt{5.62} \approx 2.37 \to \sqrt{2.37} \approx \approx 1.53$$
也就是说至多 $6$ 次就可以让数列里面的数成为 $1$,所以这个优化效果拔群。
void modify (int node, int l, int r, int s, int t) {
if (l == r) {
tree[node] = sqrt (tree[node]);
mx[node] = sqrt (mx[node]);
return ;
}
int mid = l + ((r - l) >> 1);
if (s <= mid && mx[node << 1] > 1) modify (node << 1, l, mid, s, t);
if (t > mid && mx[(node << 1) + 1] > 1) modify ((node << 1) + 1, mid + 1, r, s, t);
pushup (node);
}
权值线段树
我们都知道,线段树用来维护的是序列上的元素。那如果维护序列上的元素个数呢?这就是权值线段树。
给你一个长度为 $n$ 的正整数序列 $A$,需要你找出 $A$ 中所有满足 $i \lt j$ 且 $A_i \gt A_j$ 的 $(i,j)$ 二元组个数。
这道题维护的就是元素个数,而不是元素值。
用权值线段树解题的话,我们需要离散化,然后把每个下标看做元素值,元素值则看做下标对应元素个数。
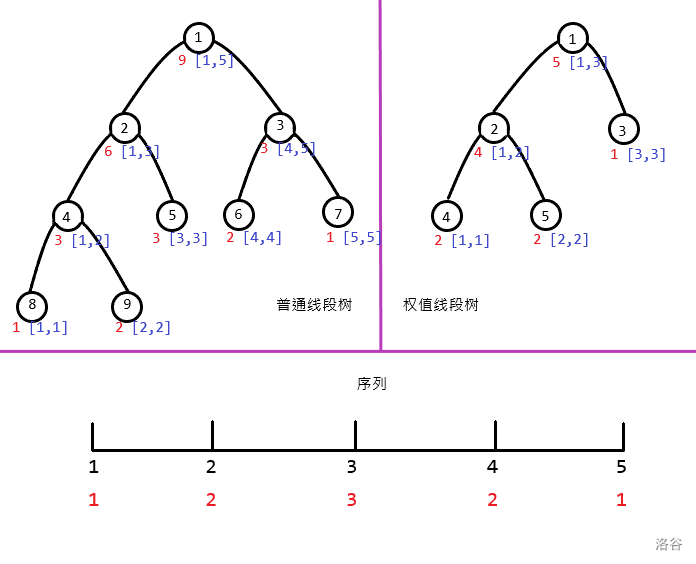
就像这样,然后我们就可以在上面做操作了。
void modify (int node, int l, int r, int c) {
if (l == r) {
tree[node]++;
return ;
}
int mid = l + ((r - l) >> 1);
if (c <= mid) modify (node << 1, l, mid, c);
else modify ((node << 1) + 1, mid + 1, r, c);
pushup (node);
}
int query (int node, int l, int r, int s, int t) {
if (s <= l && r <= t) return tree[node];
int mid = l + ((r - l) >> 1), ret = 0;
if (s <= mid) ret += query (node << 1, l, mid, s, t);
if (t > mid) ret += query ((node << 1) + 1, mid + 1, r, s, t);
pushup (node);
return ret;
}
int main () {
scanf ("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf ("%lld", &a[i]);
A[i] = a[i];
}
sort (A + 1, A + n + 1);
int ret = unique (A + 1, A + n + 1) - A - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound (A + 1, A + ret + 1, a[i]) - A;
printf ("%lld", ans);
return 0;
}
可持久化线段树
可持久化也分为部分可持久化与完全可持久化。
一般可持久化的题目都会让你记录一个历史版本,这个历史版本就是每一个操作所产生的新的线段树。
也就是说,如果我在原本的线段树上做了一个单点修改操作,那么就会多一个历史版本是操作后的线段树,版本与操作对应。
部分可持久化就是可以访问所有历史版本,但是只有最新版本可以修改。
完全可持久化就是可以访问,修改所有历史版本。
如果我们对每一个操作都开一个线段树呢?
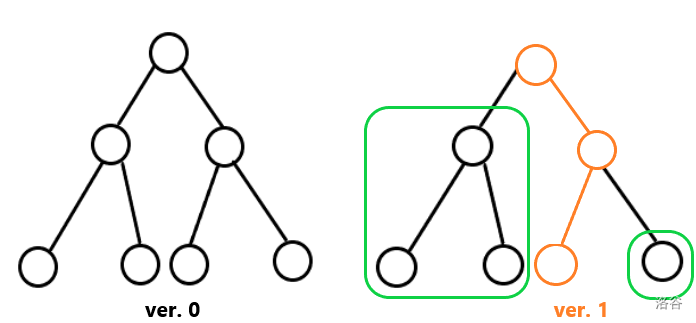
ver. 0 就是未做修改的线段树,ver. 1 是单点修改。
都知道,这样肯定会爆空间,但是我把它们与原线段树比较,发现修改经过的节点是条链。
那么我们为什么不考虑把这条链加到原线段树上面呢?
这时候,主席树(可持久化权值线段树)便应运而生了。
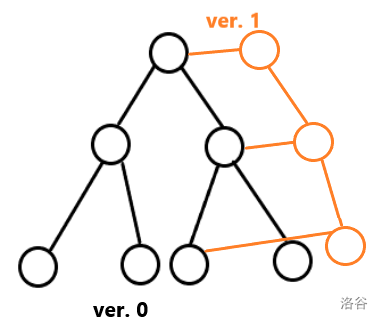
可以发现,新增的节点不仅构成了链,还连接了对应的节点。并且节点数是不超过 $\log n$ 的。
但是主席树必须要用动态开点线段树,不然空间就会像前面一样爆掉。
我们可以对每一颗新增出来的链开一个数组来记录它的根节点,方便遍历,操作基本跟线段树是一样的。
静态区间第 $k$ 小。
我们可以把这个问题拆成区间 $[1,r]$ 的静态第 $k$ 小,就可以用主席树来维护。那么如果我们要求区间 $[l,r]$,只需要用一下前缀和的思想,用 $[1,r] - [1,l-1]$ 就可以了。
注意离散化。
struct Seg {
int ls, rs;
int sum;
} tree[N * 20];
int build (int l, int r) {
int node = ++tot;
if (l == r) return node;
int mid = l + ((r - l) >> 1);
tree[node].ls = build (l, mid);
tree[node].rs = build (mid + 1, r);
return node;
}
int modify (int v, int l, int r, int s) {
int node = ++tot;
tree[node] = tree[v];
tree[node].sum++;
if (l == r) return node;
int mid = l + ((r - l) >> 1);
if (s <= mid) tree[node].ls = modify (tree[node].ls, l, mid, s);
else tree[node].rs = modify (tree[node].rs, mid + 1, r, s);
return node;
}
int query (int l, int r, int s, int t, int k) {
if (l == r) return l;
int mid = l + ((r - l) >> 1), x = tree[tree[t].ls].sum - tree[tree[s].ls].sum;
if (k <= x) return query (l, mid, tree[s].ls, tree[t].ls, k);
else return query (mid + 1, r, tree[s].rs, tree[t].rs, k - x);
}
int main () {
ios::sync_with_stdio (false);
cin.tie (0); cout.tie (0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
b[i] = a[i];
}
sort (b + 1, b + n + 1);
len = unique (b + 1, b + n + 1) - b - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound (b + 1, b + len + 1, a[i]) - b;
rt[0] = build (1, len);
for (int i = 1; i <= n; ++i) rt[i] = modify (rt[i - 1], 1, len, a[i]);
while (m--) {
int l, r, k;
cin >> l >> r >> k;
cout << b[query (1, len, rt[l - 1], rt[r], k)] << endl;
}
return 0;
}