李超线段树

用来维护线段（一次函数）信息。

值域线段树：

对于值域线段树维护\(x\)轴 上的区间\([l,r]\)，维护\(s\)，表示在\(x=mid\)处可能取最大值的线段（不一定就是最大）。

添加操作：

新边\(u\)，旧边\(v\)。

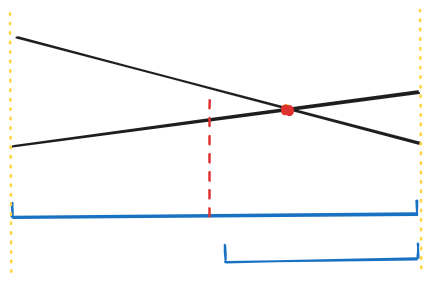
1.将边拆为最多\(\log\)个在线段树上的线段。

2.如果\(u\)与\(v\)存在完全覆盖关系，就直接去最优边。

3.如果有交点，则递归到有交点的那一侧。(\(\log\)层)

对于递归，就是在该区间去最优边，再将另一条边传到子节点。

查询操作：

记录从根到叶子节点这一条链上的最优边。

struct line{dou k, b;}L[N];
dou clac(int u, dou x){return L[u].k * x + L[u].b;}
void add(dou x, dou y, dou X, dou Y){
	if(x == X) L[++cnt] = {0, max(y, Y)};
	else L[++cnt].k = (Y - y) / (X - x), L[cnt].b = Y - L[cnt].k * X;
}
int cmp(dou x, dou y){
	if(x - y > eps) return 1;
	if(y - x > eps) return -1;
	return 0;
}

struct L_S_T{
#define ld rt * 2
#define rd rt * 2 + 1
#define mid (cl + cr >> 1)
	int s[M << 2];
	void cg(int rt, int cl, int cr, int u){
		int &v = s[rt];
		int bmid = cmp(clac(u, mid), clac(v, mid));
		if(bmid == 1 || (!bmid && u < v)) swap(u, v);
		int bl = cmp(clac(u, cl), clac(v, cl)), br = cmp(clac(u, cr), clac(v, cr));
		if(bl == 1 || (!bl && u < v)) cg(ld, cl, mid, u);
		if(br == 1 || (!br && u < v)) cg(rd, mid + 1, cr, u);
	}
	void modify(int rt, int cl, int cr, int l, int r, int u){
		if(l <= cl && r >= cr){
			cg(rt, cl, cr, u);
			return ;
		}
		if(l <= mid) modify(ld,  cl, mid, l, r, u);
		if(r > mid) modify(rd, mid + 1, cr, l, r, u);
	}
	int check(int u, int v, int x){
		if(cmp(clac(u, x), clac(v, x)) == 1) return u;
		if(cmp(clac(u, x), clac(v, x)) == 0) return min(u, v);
		return v;
	}
	int query(int rt, int cl, int cr, int k){
		int res = s[rt];
		if(cl == cr) return res;
		if(k <= mid) res = check(res, query(ld, cl, mid, k), k);
		else res = check(res, query(rd, mid + 1, cr, k), k);
		return res;
	}
}S;