$$\texttt{\color{E74C3C}戏之落幕}$$
进食中
不会树上路径交挂 100pts
Week 1
Day 1
-
题意:一个 n 的排列,找出字典序最小的操作序列使之升序。
- 操作 $\verb!a!$:将第一个元素压入栈 $S_1$。
- 操作 $\verb!b!$:将 $S_1$ 栈顶元素弹出至输出序列。
- 操作 $\verb!c!$:将第一个元素压入栈 $S_2$。
- 操作 $\verb!d!$:将 $S_2$ 栈顶元素弹出至输出序列。
Sol:找出矛盾逻辑关系,建边后二分图染色
-
题意: $\gcd(a,b) = 1$ ,求第 $k$ 大不能被 $ax+by$ 表示的数($a,b \ge0$)
Sol:
由其易知最大不能表示的数为 $a\times b-a-b$,打表发现答案是 $a\times b-a-b$ 减去第 $k$ 小能表示的数。
二分加上
check复杂度为 $O(n\log n)$ ,不能通过,考虑优化1.考虑 $i = 1\dots a$ ,统计 $((i-1)b,ib]$ 中可以被表示的数,形如 $m=ax+by$ ,若 $y!=0$ ,则可以由上一块直接转移过来,考虑每次新增的数仅为只能用 $ay$ 表示的数,复杂度 $O(n)$
2.容易发现
check里要求出 $\sum\limits_{i=0}^n \left \lfloor \frac{k+ai}{b} \right \rfloor$ ,可用类欧几里得算法优化至 $O(\log n)$,总时间复杂度 $O(\log^2 n)$
*
题意:一棵以 $1$ 为根的树,边有边权,每个节点有类型 $c$ 。定义 $f(c)$ 为类型 $c$ 两两树上最短路之和,
对于每个 $i$ ,求出以 $i$ 为根的子树中最大的 $f(c)$ 对应的 $c$ ,及编号及 $c$ 第 $k_i$ 小的 $f(c)$ 。Sol:一个
Simple的线段树合并。
Day 2
-
题意:一个无向图,每次查询的时候给一堆二元组 $(x_i,y_i)$。
求图中有多少个点 $u$ 与至少一个这次询问给出的二元组 $(x_i,y_i)$ 满足
$\mathrm{dist}(u,x_i)\leq y_i$,$\mathrm{dist}$ 表示这两个点在图中的距离。
如果不连通 $\mathrm{dist} = +\infty$。Sol:设 $f[i][j]$ 为 $dis(i,u)\le j$ 的 $u$ 的集合,容易发现可以用
bitset维护,复杂度 $O(\frac{n^3}{w})$ -
题意:圆上有 $n$ 个数,若 $i,j(i \neq j)$ 满足某一圆弧 $i$ 及 $j$ 中不存在 $a_k > \min(a_i,a_j)$ ,则两个数可以相互看见,求总数。
Sol:断环为链,把最大的放最前面,重点是单调栈。维护单调递减的单调栈,每次弹出时造成 1 贡献,入栈时若栈内还有数则他俩可以互相看到,加上 1 贡献,注意大小相同的数合并。
-
题意:有 $n$ 个车站,告诉你第 $i$ 个车站可以到$[i+1,a_i]$ 。若 $p[i][j]$ 为从i到j最小车票花费,求所有$p[i][j]$ 的和。
Sol:感性理解贪心选 $[i+1,a_i]$ 中 $a_k$ 最大的,转移的话 $f_i=f_k+(k−i)+(n−a_i)$ 。 -
题意:$a_1\dots a_n$ ,单点修改,全局查询 $a_i\ge k$ 形成的连通块数。
Sol:联通块数 = 点数 - 边数。点数即为 $\sum\limits_{i=1}^{n}[a_i\ge x]$ ,两点之间有边当且仅当 $\min(a_i,a_{i+1}) \ge x$ ,开两棵平衡树分别维护即可。
-
题意 $A_i,B_i,C_i$,每次选择一个区间 $[l,r]$,
- $A_i=A_i+B_i$。
- 令 $B_i=B_i+C_i$。
- 令 $C_i=C_i+A_i$。
- 令 $A_i=A_i+v$。
- 令 $B_i=B_i\times v$。
- 令 $C_i=v$。
- 查询 $[l,r] $ 区间和
Sol:首先矩阵满足分配律,其次这是区间矩阵乘,同时查询区间和,线段树维护即可。
-
题意:请写一个程序,要求维护一个数列,支持以下 $6$ 种操作:
编号 名称 格式 说明 1 插入 $\operatorname{INSERT}\ posi \ tot \ c_1 \ c_2 \cdots c_{tot}$ 在当前数列的第 $posi$ 个数字后插入 $tot$ 个数字:$c_1, c_2 \cdots c_{tot}$;若在数列首插入,则 $posi$ 为 $0$ 2 删除 $\operatorname{DELETE} \ posi \ tot$ 从当前数列的第 $posi$ 个数字开始连续删除 $tot$ 个数字 3 修改 $\operatorname{MAKE-SAME} \ posi \ tot \ c$ 从当前数列的第 $posi$ 个数字开始的连续 $tot$ 个数字统一修改为 $c$ 4 翻转 $\operatorname{REVERSE} \ posi \ tot$ 取出从当前数列的第 $posi$ 个数字开始的 $tot$ 个数字,翻转后放入原来的位置 5 求和 $\operatorname{GET-SUM} \ posi \ tot$ 计算从当前数列的第 $posi$ 个数字开始的 $tot$ 个数字的和并输出 6 求最大子列和 $\operatorname{MAX-SUM}$ 求出当前数列中和最大的一段子列,并输出最大和 Sol:写起来似乎没那么恶心,对于一次连续插入要建完树之后再插入,关键在于
pushup。 -
题意:区间异或,区间异或最大值。
Sol:区间异或考虑差分,令 $b_i = a_i\oplus a_{i-1}$ ,这样变为单点修改,值得说的是因为 $a_i = b_1\oplus\dots\oplus b_i$ ,所以 $a_l\dots a_r$ 的线性基和 $a_l \cup b_{[l+1,r]}$ 线性基相同。
-
题意:等概率随机在 $[L,R]$ 中选出一个整数作为伤害值 $d$,对所有随从造成 $d$ 点伤害,如果有随从死亡,则再次施放该法术,但伤害值不重新随机;如果没有随从死亡,则停止释放。
共进行 $m$ 次如下类型的操作:
- 在场面上加入一个血量为 $h$ 的随从,这里随从的血量都不能超过 $n$;
- 给定 $L, R$,询问亵渎期望触发多少次;
Sol:调和级数,把区间放到线段树上,然后卡常。
Day 3
-
题意:树上单点区间修改,链区间查询。
Sol:不带修的话可以把主席树上树然后树上前缀和,带修的话考虑树剖然后树状数组套线段树,虽然是 $O(n\log^3n)$ ,但是树剖
log跑不满,树状数组常数小,理论能过。 -
题意:一个无向图,求三条起点终点相同的点边均不相交路径。
Sol:先建成一棵树,非树边即为链加,一条边被加了两次就可以拎出来了,这时候起点和终点都已知,直接建图网络流找路径。
Day 4
-
P2627 [USACO11OPEN] Mowing the Lawn G
题意:Farmer John 有 $N$($1\le N\le 10^5$)只排成一排的奶牛,编号为 $1\ldots N$。每只奶牛的效率是不同的,奶牛 $i$ 的效率为 $E_i$($0\le E_i\le 10^9$)。计算 FJ 可以得到的最大效率,并且该方案中没有连续的超过 $K$ 只奶牛。
Sol:比较 simple 的解法就不说了。我们设 $f_{i,j}$ 为以 $i$ 为结尾,已经连续 $j$ 个的最大答案,那么 $f_{i,j} = f_{i-1,j-1}+e_i$ ,很容易的用滚动数组滚掉一维,容易发现对于转移柿子 $f_i=f_{i-1}+e_i$ ,每次就是将 $f_{1\dots n-1}$ 整体右移一位再加上 $e_i$ ,直接用平衡树维护就好了。
-
题意:$N (1\le N\le1000)$ 个目标点,目标点 $i$ 在目标点 $x_i$,该点得分为 $p_i$。贝西开始时可以选择站在一个目标点上,只允许朝一个方向跳跃,从一目标点跳到另外一个目标点,每次跳跃的距离至少和上一次跳跃的距离相等,并且必须跳到一个目标点。每跳到一个目标点,贝西可以拿到该点的得分,请计算他的最大可能得分。
Sol:设 $f_{i,j}$ 为从 $j$ 跳到 $i$ 得到的最大得分,然后单调队列或者线段树优化一下就好了。
-
题意:一棵树,从根节点移动 $k$ 步最多能经过多少节点,节点可以重复经过多次,但不重复计数。
Sol:树上背包,设 $f_{i,j,0/1}$ 为从 $i$ 出发走 $j$ 步,是否回到 $i$ 节点,能经过最多节点数,那么 $f_{x,j,0} = \max(f_{x,j-k,1}+f_{y,k-1,0},f_{x,j-k,0}+f_{y,k-2,1})$ ,$f_{x,j,1}$ 同理。
-
题意:一开始空中有 $N$ 个彩蛋,对于第 $i$ 个彩蛋,他的初始位置用整数坐标 $(x_{i}, y_{i})$ 表示,游戏开始后,它匀速沿 $y$ 轴负方向下落,速度为 $v_{i}$ 单位距离/单位时间。Sue 的初始位置为 $(x_{0}, 0)$,Sue 可以沿 $x$ 轴的正方向或负方向移动,Sue 的移动速度是 $1$ 单位距离/单位时间,得分为当前彩蛋的 $y$ 坐标的千分之一。在收集到所有彩蛋的基础上,得到的分数最高。
Sol:P1220 关路灯的经验,容易发现已被收集彩蛋的区间是连续的一段,考虑 $f_{i,j,0/1}$ 为收集完 $[i,j]$ 的彩蛋,目前在 $i/j$ 处的最小代价,转移从 $f_{i+1,j}$ 和 $f_{i,j-1}$ 转移。
-
题意:有一棵点数为 $n$ 的树,树边有边权。给你一个在 $0 \sim n$ 之内的正整数 $k$ ,你要在这棵树中选择 $k$ 个点,将其染成黑色,并将其他的 $n-k$ 个点染成白色。将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间的距离的和的收益。问收益最大值是多少。
Sol:好题,点与点之间的贡献是有后效性的,难以转移,考虑统计边的贡献,对于一条边 $(u,v)$ ,其贡献次数为 $v$ 中黑点与 $v$ 外黑点的乘积加上 $v$ 中白点与 $v$ 外白点的乘积,树上背包转移即可。
-
题意:一棵树,若一点放监听器,则于其直接相邻的点皆被监听(本身不被监听),求放 $k$ 个监听器使得所有点都被监听的方案数。
Sol:设 $f_{i,j,0/1,0/1}$ 为 $i$ 子树内放了 $j$ 个监听器,$i$ 是否被监听,$i$ 是否放监听器,使得其子树内节点均被监听的方案树,同样树上背包转移。
-
题意:有 $N$ 个村庄坐落在一条直线上,第 $i(i>1)$ 个村庄距离第 $1$ 个村庄的距离为 $D_i$。需要在这些村庄中建立不超过 $K$ 个通讯基站,在第 $i$ 个村庄建立基站的费用为 $C_i$。如果在距离第 $i$ 个村庄不超过 $S_i$ 的范围内建立了一个通讯基站,那么就村庄被基站覆盖了。如果第 $i$ 个村庄没有被覆盖,则需要向他们补偿,费用为 $W_i$。现在的问题是,选择基站的位置,使得总费用最小。
Sol:设 $f_{i,j}$ 为在 $i$ 建立第 $j$ 个基站最小费用,考虑转移 $f_{i,j} = f_{k,j-1}+cost(k+1,i)$ ,唯一难算的 $cost(j+1,i)$ 用线段树维护一下就好了。
Day 5
-
题意:一棵树,有若干边上有单向收费站,每次经过付费 1 元,初始在 1 节点,依次前往 $s_1,\dotsb,s_n$ ,求总花费。
Sol:树上差分。
-
题意:一棵树,边有边权。求删除每一条边后形成的最长路的和。最长路可理解为带权树的直径。
Sol:换根
dp -
题意:现在我们有一个长度为 $n$ 的整数序列 $a$。但是它太不好看了,于是我们希望把它变成一个单调严格上升的序列。但是不希望改变过多的数,也不希望改变的幅度太大。
Sol:第一问将 $a_i = a_i-i$ 后求最长不降子序列即可,第二问有些难度。设 $l_i$ 是以 $a_i$ 为结尾最长子序列长度,$f_i$ 是以 $a_i$ 为结尾且 $[1,i]$ 均符合条件的最小代价,转移则是 $f_i = \min(f_{j满足 l_j +1 = l_i ,b_j \le b_i,j < i}+W(j+1,i-1))$ ,一个结论就是将 $[j+1,i-1]$ 中的数变为单调不降,最优方案之一一定是前一部分变为 $b_j$ ,后一部分变为 $b_i$ ,记得让 $b_0 = -INF$,$b_{n+1} = INF$ 。
-
题意:
做每道菜所需的时间是和前一道菜有关的,若前一道菜的对应的口味是 $a$,这一道为 $b$,则做这道菜所需的时间为 $a\oplus b$ 。队伍中的第 $i$ 个同学,最多允许紧跟他身后的 $B_i$ 个人先拿到饭菜。一旦在此之后的任意同学比当前同学先拿到饭,当前同学将会十分愤怒。因此,食堂做菜还得照顾到同学们的情绪。 现在,小 F 想知道在满足所有人的容忍度这一前提下,自己的学校食堂做完这些菜最少需要多少时间。Sol:由于 $B_i$ 很小,所以考虑状压,设 $f_{i,j,k}$ 为处理到第 $i$ 个人,他及后面 7 人是否拿到饭的状态 $j$,以及上一个拿到饭的人和 $i$ 的相对距离 $k$ ,然后正常转移就好了。
-
题意:位置在 $i$ 的人面前的第 $j$ 堆的石子的数量,刚好是 $i$ 写成 $K$ 进制后的第 $j$ 位。商场会给方伯伯两个整数 $L,R$。方伯伯要把位置在 $[L, R]$ 中的每个人的石子都合并成一堆石子。每次操作,他可以选择一个人面前的两堆石子,将其中的一堆中的某些石子移动到另一堆,代价是移动的石子数量 $\times$ 移动的距离。想请你告诉他最少的代价是多少。
Sol:假若给定转移位置的话可以很好的数位
dp,但是不行,所以先指定转移到第 1 位,然后往右dp贪心取最大的就好了。
Day 6
一些小花:A cin 卡掉 60 分,B spj .ans 写成 .out ,数据还贼 jb 水,真没素质。
-
题意:给 $n$ 个点,求出任意两点间曼哈顿距离比上欧几里得距离的最大值
Sol :我们设 $X = |x_i-x_j|$ ,$Y = |y_i-y_j|$ ,则 $X = Y$ 时最大,这时对应弧度为 $\frac{\pi}{4}$ 或 $\frac{3\pi}{4}$ ,旋转一下往后找几个点取最大值即可。
-
题意:给定 $n,k$ ,节点编号由 $0$ 到 $n-1$,可以执行下面操作若干次,每次选定 $u,v$ ,同时连接 $(u,v)$ 和 $((u+k)\bmod n,(v+k)\bmod n)$ 。构造一种连接方式将该图连为一棵树,若无解输出
-1Sol:水水的小构造一枚啊,容易发现偶数无解,奇数可以拉出 $\gcd(n,k)$ 条长度为 $\frac{n}{\gcd(n,k)}$ 的链,然后按下图方式连接即可。
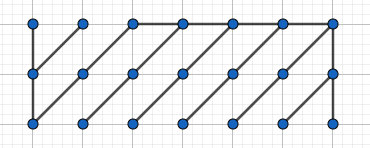
什么你说 $\gcd(n,k) > \frac{n}{\gcd(n,k)}$ 时不对,你把图转 $90\degree$ 不是一样的连法?
-
题意:按照如下方式生成一个序列,操作共执行 $n$ 次,初始时序列为空:
-
等概率随机选择一个空位(若当前有 $k$ 个字符,则有 $k+1$ 个空位,每个空位选中的概率为 $\frac{1}{k+1}$)。
-
以 $p$ 的概率在空位上插入字符串
()或以 $1-p$ 的概率插入字符串)(。求最后是合法括号匹配的答案概率,对 $998244353$ 取模
Sol:假如
(为 $1$,)为 $−1$,那么一个序列合法的充要条件为:最小前缀和为 $0$,且以 $0$ 结尾。
现在考虑维护这些前缀和。
如果我们在当前序列某一位后插入一个
标签:frac,题意,sum,Sol,times,test,节点 From: https://www.cnblogs.com/ZepX-D/p/18303455(),且那一位的前缀和为 $ -