树链剖分

引言

第一次接触树链/重链剖分的时候还是学习 \(Lca\), 没系统性的看过剖分, 今天刚重新学习了一下, 还是比较神奇的, 没想到一个树形结构能有这么多种神奇的操作, 总的来说, 树链剖分还是比较重要的一个策略

正文

定义

先给出图示

首先我们给出以下几个定义:

• 重儿子, 对于一个非叶子节点, 它的重儿子我们定义为, 以该节点为根的组成的子树大小最大的节点为重儿子, 例如图示中加粗的节点, 显然重儿子对于一个树来说只有一个
• 轻儿子, 对于一个非叶子节点, 除了重儿子就是轻儿子
• 重边, 由两个的重儿子组成的链称之为重边, 例如图示中的\((a, b)\), \((b, e)\) , 链中均为重儿子且连续
• 重链, 由连续的重边组成的链称为重链, 相邻节点均为父子关系, 例如图中的加粗链即是重链
• 轻边, 除了重边之外的边称为轻边, 两条重链之间存在一条轻边
• 链头, 重链的起点, 换句话说就是深度最浅的重儿子, 例如重链 \((a, b, e, j, q)\) 中, \(a\) 节点最浅, 故为链头

原理

利用上面剖好的链, 我们树形结构形成的重链不过超过 \(logn\) 条, 那么我们可以利用该性质, 从某个节点沿着各个链开始跳, 每次跳到链头, 最多只需要 \(logn\) 次就能到达根节点, 由于两个重链之间存在轻边, 那么也就是经过的轻边也小于 \(logn\) 条
下面给出证明:
从叶子节点出发, 考虑二叉树, 对于一条轻边, 其形成的子树大小必然小于 \(\frac{n}{2}\) 大小, 那么考虑两条重链开始跳, 从一条重链跳到另一条重链势必要经过一条轻边, 那么其子树大小必然会缩小到小于 \(\frac{1}{2}\), 这样我们最多经过 \(logn\) 条轻边即可到达根节点. 那么对于多叉树, 其缩小的范围会更大, 也就是不会超过 \(logn\) 条轻边

树剖求 \(LCA\)

考虑如何求 \(LCA\), 对于两个点 \(a, b\), 有以下步骤:

• 如果 \(a, b\) 的链头不一样, 那么谁的链头更深谁往上跳, 跳的时候可直接跳过轻边, 因为每个链头都是轻儿子, 则其父节点一定是重儿子, 依次递归
• \(a, b\) 在同一条重链上, 那么只需要比较谁的深度更浅即可, 浅的那个为最近公共祖先节点

代码

\(dfs1\) 是求出每个子树的大小 \(sz\) 以及每个节点的父节点 \(fa\), 还有重儿子 \(son\), 每个节点距离根节点的深度 \(dep\)
\(dfs2\) 是对每条重链都标记上链头 \(top\), 如果其有重儿子, 则直接递归, 一条重链上每个重儿子的链头都是一样的, 初始的链头是轻儿子
\(lca\) 即上述过程

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
int dep[N], top[N], fa[N], sz[N], son[N];
vector<int> g[N];
void dfs1(int u){
    sz[u] = 1, dep[u] = dep[fa[u]] + 1;
    for (auto x : g[u]){
        if (x == fa[u]) continue;
        fa[x] = u;
        dfs1(x);
        sz[u] += sz[x];
        if (sz[x] > sz[son[u]]) son[u] = x;
    }
}
void dfs2(int u, int h){
    top[u] = h;
    if (son[u]) dfs2(son[u], h);
    for (auto x : g[u]){
        if (x == fa[u] || x == son[u]) continue;
        dfs2(x, x);
    }
}
int lca(int a, int b){
    while (top[a] != top[b]){
        if (dep[top[a]] > dep[top[b]]) a = fa[top[a]];
        else b = fa[top[b]];
    }
    return dep[a] > dep[b] ? b : a;
}
signed main(){
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, m, s; cin >> n >> m >> s;
    for (int i = 1; i <= n - 1; i++){
        int a, b; cin >> a >> b;
        g[a].push_back(b), g[b].push_back(a);
    }
    dfs1(s), dfs2(s, s);
    while (m--){
        int a, b;
        cin >> a >> b;
        cout << lca(a, b) << '\n';
    }
    return 0;
}

例题

P1. 重链剖分/树链剖分
在树剖过程中还有一些奇妙的性质, 例如一条重链中的节点均符合 \(dfs\) 序, 那么就可以根据 \(dfs\) 序进行某些操作, 具体操作在下面的例题中详细给出

【模板】重链剖分/树链剖分

题目描述

如题，已知一棵包含 \(N\) 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

• 1 x y z，表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。

• 2 x y，表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。

• 3 x z，表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。

• 4 x 表示求以 \(x\) 为根节点的子树内所有节点值之和

输入格式

第一行包含 \(4\) 个正整数 \(N,M,R,P\)，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含 \(N\) 个非负整数，分别依次表示各个节点上初始的数值。

接下来 \(N-1\) 行每行包含两个整数 \(x,y\)，表示点 \(x\) 和点 \(y\) 之间连有一条边（保证无环且连通）。

接下来 \(M\) 行每行包含若干个正整数，每行表示一个操作。

输出格式

输出包含若干行，分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果（对 \(P\) 取模）。

样例 #1

样例输入 #1

5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

样例输出 #1

2
21

提示

【数据规模】

对于 \(30\%\) 的数据： \(1 \leq N \leq 10\)，\(1 \leq M \leq 10\)；

对于 \(70\%\) 的数据： \(1 \leq N \leq {10}^3\)，\(1 \leq M \leq {10}^3\)；

对于 \(100\%\) 的数据： \(1\le N \leq {10}^5\)，\(1\le M \leq {10}^5\)，\(1\le R\le N\)，\(1\le P \le 2^{30}\)。所有输入的数均在 int 范围内。

【样例说明】

树的结构如下：

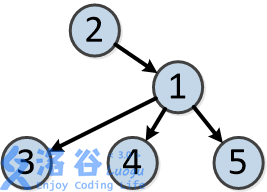
各个操作如下：

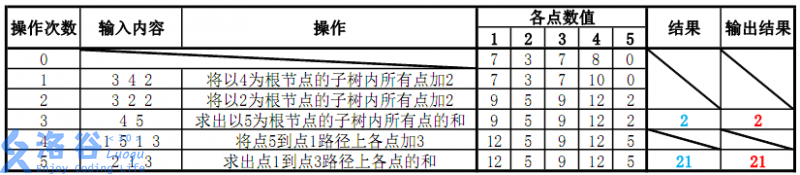
故输出应依次为 \(2\) 和 \(21\)。

思路

上述题目中, 由于要进行一整个子树