变分自编码器（六）：从几何视角来理解VAE的尝试

前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？

对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。

笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。

自编码器 #

我们从自编码器（AutoEncoder，AE）出发。自编码器的初衷是为了数据降维，假设原始特征$x$维度过高，那么我们希望通过编码器$E$将其编码成低维特征向量$z=E(x)$，编码的原则是尽可能保留原始信息，因此我们再训练一个解码器$D$，希望能通过$z$重构原始信息，即$x\approx D(E(x))$，其优化目标一般是
\begin{equation}E,D = \mathop{\arg\min}_{E,D}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert x - D(E(x))\Vert^2\big]\end{equation}
对应的示意图如下：

自编码器示意图

编码空间 #

假如每个样本都可以重构得很好，那么我们可以将$z$当作是$x$的等价表示，也就是说把$z$研究好了就相当于把$x$研究好了。现在我们将每个$x$都编码出对应的特征向量$z$，然后我们关心一个问题：这些$z$覆盖的空间“长什么样”？

经过自编码器后，原始样本对应编码空间中的一个点

为什么要关心这个问题呢？因为我们可以有很多不同的编码方式，不同编码方式得到的特征向量也有好坏之分，从“编码空间长什么样”我们可以大致地看出特征向量的好坏。比如下面四个不同的编码向量的分布形状模拟图：

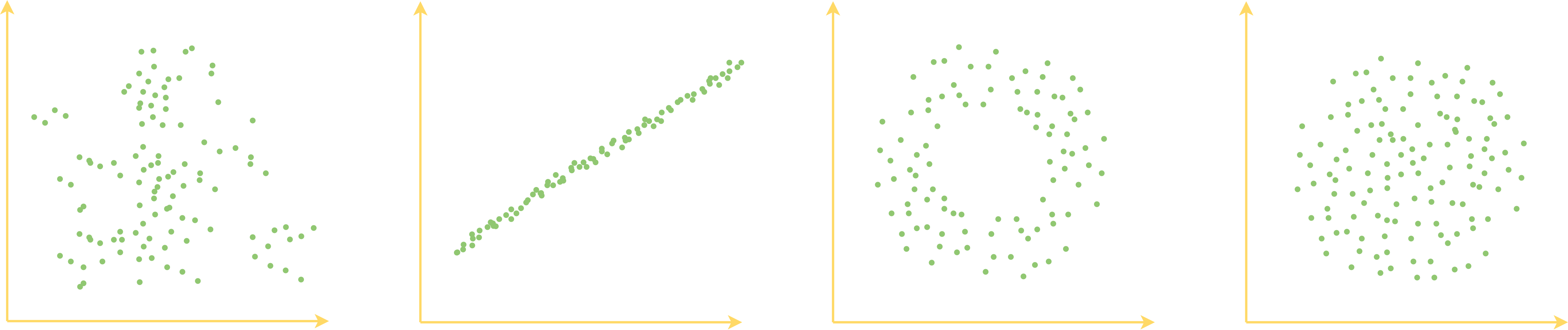
四种不同的编码空间形状模拟图，分别代表无规律、线形、环形、圆形

第一个图的向量分布没什么特别的形状，比较散乱，说明编码空间并不是特别规整；第二个图的向量集中在一条线上，说明其实编码向量的维度之间存在冗余；第三个图是一个环形，说明其圆心附近并没有对应的真实样本；第四个图是一个圆形，表明它比较规整地覆盖了一块连续空间。就四个图来看，我们认为最后一个图所描绘的向量分布形状是最理想的：规整、无冗余、连续，这意味着我们从中学习了一部分样本，就很容易泛化到未知的新样本上去，因为我们知道编码空间是规整连续的，所以我们知道训练样本的编码向量之间的“缝隙”（图中的两个点之间的空白部分），实际上也对应着未知的真实样本，因此把已知的搞好了，很可能未知的也搞好了。

从点到面 #

总的来说，大体上我们关心编码空间的如下问题：

1、所有编码向量覆盖一个怎样的区域？

2、是否有未知的真实样本对应空白之处的向量？

3、有没有“脱离群众”的向量？

4、有没有办法让编码空间更规整一些？

常规的自编码器由于没有特别的约束，因此很难回答上述问题。于是，变分自编码器出来了，从编码角度来看，它的目的是：1、让编码空间更规整一些；2、让编码向量更紧凑一些。为了达到这个目的，变分自编码器先引入了后验分布$p(z|x)$。

对于不想深究概率语言的读者来说，该怎么理解后验分布$p(z|x)$呢？直观来看，我们可以将后验分布理解为一个“椭圆”，原来每个样本对应着一个编码向量，也就是编码空间中的一个点，引入后验分布之后，相对于说现在每个样本$x$都对应一个“椭圆”。刚才我们说希望编码向量更“紧凑”一些，但理论上来讲，再多的“点”也没有办法把一个“面”覆盖完，但要是用“面”来覆盖“面”，那么就容易把目标覆盖住了。这就是变分自编码器做出的主要改动之一。

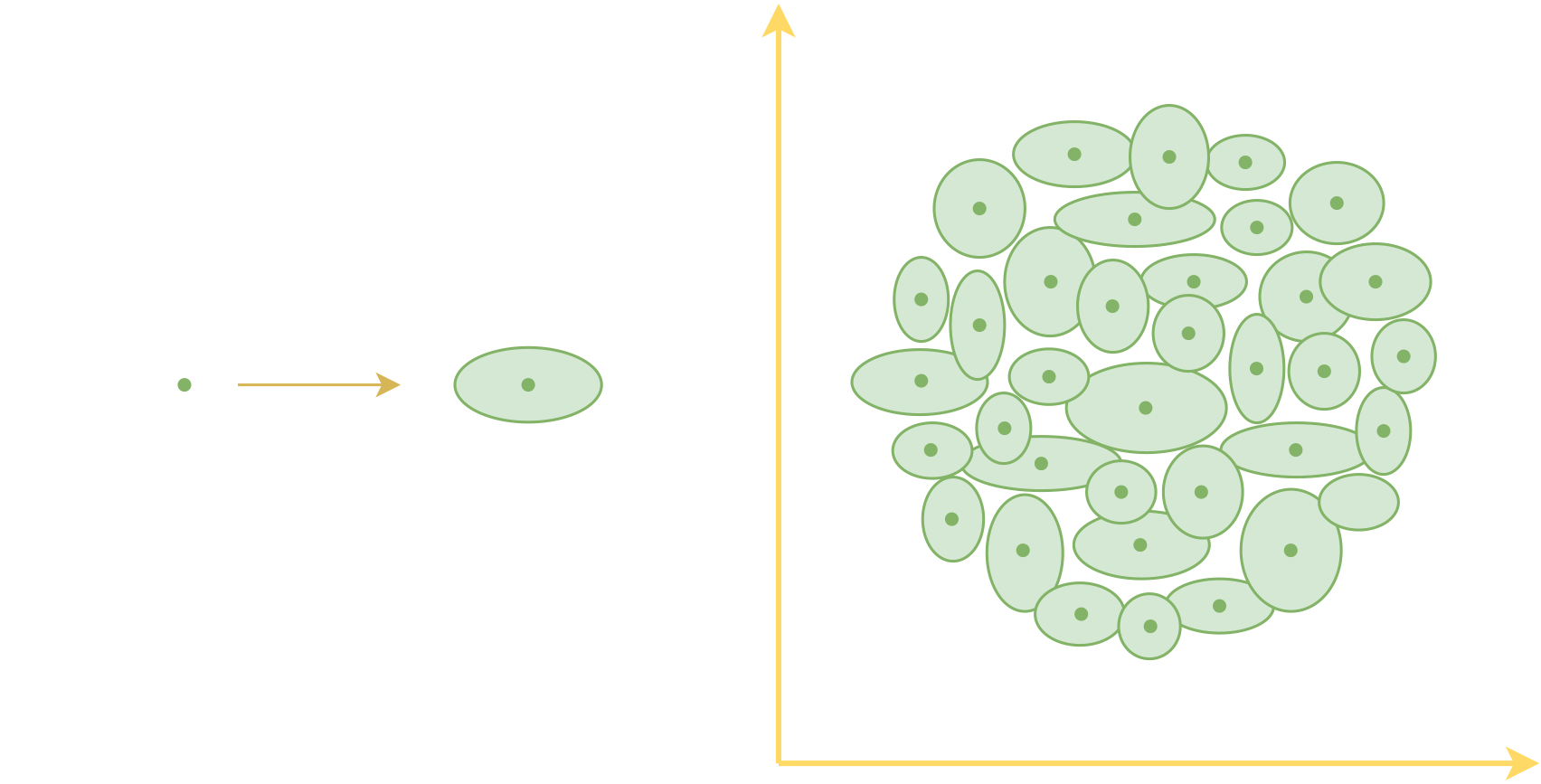
每个样本的编码从一个点变成了一个面（椭圆），于是原本由点覆盖的编码空间变成了由面覆盖

读者可能会问，为什么非得要椭圆呢？矩形或者其他形状可以吗？回到概率语言上，椭圆对应着“假设$p(z|x)$各分量独立的高斯分布”，从概率的角度来看，高斯分布是比较容易处理的一类概率分布，所以我们用高斯分布，也就对应着椭圆，其他形状也就对应这其他分布，比如矩形可以跟均匀分布对应，但后面再算KL散度的时候会比较麻烦，因此一般不使用。

采样重构 #

现在每个样本$x$都对应一个“椭圆”，而确定一个“椭圆”需要两个信息：椭圆中心、椭圆轴长，它们各自构成一个向量，并且这个向量依赖于样本$x$，我们将其记为$\mu(x),\sigma(x)$。既然整个椭圆都对应着样本$x$，我们要求椭圆内任意一点都可以重构$x$，所以训练目标为：
\begin{equation}\mu,\sigma,D = \mathop{\arg\min}_{\mu,\sigma,D}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert x - D(\mu(x) + \varepsilon\otimes \sigma(x))\Vert^2\big],\quad \varepsilon\sim \mathcal{N}(0, 1)\end{equation}
其中$\mathcal{D}$是训练数据，$\mathcal{N}(0, 1)$为标准正态分布，我们可以将它理解为一个单位圆，也就是说，我们先从单位圆内采样$\varepsilon$，然后通过平移缩放变换$\mu(x) + \varepsilon\otimes \sigma(x)$将其变为“中心为$\mu(x)$、轴长为$\sigma(x)$”的椭圆内的点，这个过程就是所谓的“重参数（Reparameterization）”。

这里的$\mu(x)$其实就对应于自编码器中的编码器$E(x)$，$\sigma(x)$相当于它能泛化的范围。

空间正则 #

最后，“椭圆”可以“让编码向量更紧凑”，但还不能“让编码空间更规整”。现在我们希望编码向量满足标准正态分布（可以将它理解为一个单位圆），即所有的椭圆覆盖的空间组成一个单位圆。

为此，我们希望每个椭圆都能向单位圆靠近，单位圆的中心为0，半径为1，所以一个基本想法是引入正则项：
\begin{equation}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert \mu(x) - 0\Vert^2 + \Vert \sigma(x) - 1\Vert^2\big]\end{equation}
事实上，这前面两项loss结合起来，就已经非常接近标准的变分自编码器了。标准的变分自编码器用了一个复杂一些、功能类似的正则项：
\begin{equation}\mathbb{E}_{x\sim \mathcal{D}}\left[\sum_{i=1}^d \frac{1}{2}\Big(\mu_{i}^2(x) + \sigma_{i}^2(x) - \log \sigma_{i}^2(x) - 1\Big)\right]\end{equation}
这个正则项来源于两个高斯分布的KL散度，所以通常也叫“KL散度项”。

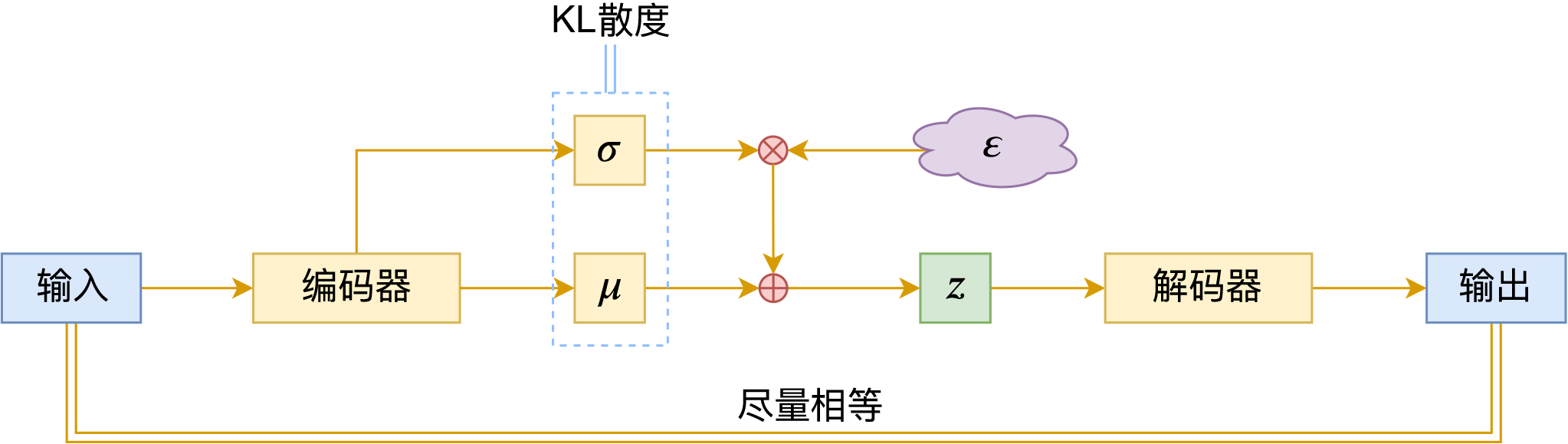
变分自编码器示意图

将两项目标组合起来，就得到最终的变分自编码器了：
\begin{equation}\Vert x - D(\mu(x) + \varepsilon\otimes \sigma(x))\Vert^2 + \sum_{i=1}^d \frac{1}{2}\Big(\mu_{i}^2(x) + \sigma_{i}^2(x) - \log \sigma_{i}^2(x) - 1\Big), \quad \varepsilon\sim \mathcal{N}(0, 1)\end{equation}

文章总结 #

本文从几何类比的角度介绍了对变分自编码器（VAE）的理解，在此视角下，变分自编码器的目标是让编码向量更加紧凑，并规范了编码分布为标准正态分布（单位圆）。

这样一来，VAE能达到两个效果：1、从标准高斯分布（单位圆）随机采样一个向量，就可以由解码器得到真实样本，即实现了生成模型；2、由于编码空间的紧凑形以及训练时对编码向量所加入的噪声，使得编码向量的各个分量能做到一定程度的解耦，并赋予编码向量一定的线性运算性质。

几何视角能让我们快速地把握变分自编码器的关键特性，降低入门难度，但也有一定的不严谨之处。如有不妥当的地方，还请读者理解并指出。

转载到请包括本文地址：https://spaces.ac.cn/archives/7725

更详细的转载事宜请参考：《科学空间FAQ》