前情提要:题解尽可能的写详细了,但是有些证明写着太费时间就没写了喵
本来\(pyb\)想让我弄一个数据结构专题,结果发现我前阵子做的那些列表里的题,每一个的提交记录里都有\(jsy\),很多题里有\(xcy\)。。。
实在整不出什么花活了,太菜了没做啥大家都没做过的题 qwq,完全的水题选讲
关注LuoyuSitfitw谢谢喵 ο(=•ω<=)ρ⌒☆,题解会在这个博客内同步更新

#5982. Gym 102341B Bulbasaur
首先最大流=最小割,那么\(f(i,j)\)就是问至少删除多少个点能使得\(i\)层和\(j\)层不连通,从小到大枚举当前层\(d\),设\(dp[s][i]\)表示删除\(i\)个点后,\(f(x,d)=i\)的最大的\(x\),然后转移即可,答案可以用这个算出
这东西麻烦的是具体的转移,可能会破防
\(O(2^KNK)\)
CF1383F Special Edges
最大流=最小割,题目转换为求最小割,发现\(k\)的范围很小,支持状压,于是考虑状压\(S\)表示\(S\)中的附加边在最小割中
对于当前状态\(S\),将\(S\)中的附加边边权设为\(0\),表示割掉了,不属于\(S\)的中附加边就设为\(INF\)
然后跑最大流,查询的时候枚举这个\(S\)算答案即可
实现上,为了复杂度,设\(INF=25\),若\(S\)下割了一条\(INF\)的边\(e\),显然取\(S\cup e\)更优,所以可以这样
然后算\(S\)的最大流时,可以先算出从\(S-lowbit(S)\),就直接改变一个点的边权然后跑即可
\(O(2^kwm+q2^k)\),然后十分卡常,我至今没过喵qwq
#4370. [AGC012F] Prefix Median
首先,肯定能大概感受到\(b_i\)会有一个上界和下界,当\(a\)按照升序排序时,\(b_i\)取到下界,\(a\)按照降序排序时,\(b_i\)取到上界
从\(a\)映射到\(b\)没前途,看能否从\(b\)还原回\(a\),也即判断合法\(b\)
将\(a\)变成一个自动排序的序列,若我们已构造出满足\(b_{[1,i-1]}\)的合法的\(a_{[1,2(i-1)-1]}\),考虑如何满足\(b_i\)
若\(b_i\)对应的值已在\(a\)中,那么只需要从未放入\(a\)中的值中选出两个最小或最大的来调整\(b_i\)这个值在\(a\)中的位置
若不在\(a\)中,则先把这个值放入\(a\)中,再加一个调整位置的值
而\(b_{i-1}\)的取值是\(a_{i-1}\),\(b_i\)的取值是\(a_i\),那么加入新的两个值后,\(a_{i-1}\)最多变到\(a_{i+1}\),也就是说,不可能存在一个值介于\(b_{i-1}\)和\(b_i\)之间,也即不存在\(j<i\)满足\(min(b_{i-1},b_i)<b_j<max(b_{i-1},b_i)\),对于那些不是\(b\)的值,因为我们取的是最小/最大值来调整且我们已经求出了一个上下界,所以也不会介于两者之间,分讨反证
整理一下就是每个\(b_i\)有一个上下界,且要满足\(\nexists j<i,min(b_{i-1},b_i)<b_j<max(b_{i-1},b_i)\)
用\(dp[i][l][r]\)表示选了\([i,n]\)中的点后,当前点可选的值,一侧有\(l\)个,另一侧有\(r\)个
\(O(N^4)\)
#6451. APIO2016 烟火表演
\(slope\ trick\)
设\(dp[x][i]\)表示以\(x\)为根的子树,需要\(i\)秒来引爆
考虑\(x\)对其父亲\(y\)的贡献:
\[dp[y][i]+=min_{j\leq i}\{dp[x][j]+|w+j-i|\} \]首先,对于同一个\(x\),\(dp[x][i]\)肯定是凸函数的形式,证明考虑归纳,若\(x\)是叶子,这点显然,然后合并到\(y\)的时候,\(dp[x][j]\)是凸的\(|w+j-i|\)是凸的,所以合并起来就是凸的,且是下凸的,还可以发现,相邻两点的值的差\(\geq1\)
这样暴力的转移肯定就爆了,所以考虑找点性质来优化转移
首先大概能感受到一些性质:
- 当\(i\)较小的时候,最优的策略肯定是把\(w\)缩小
- 当\(i\)较大的时候,最优策略就是把\(w\)尽可能扩大
- 当\(i\)居中的时候,最优策略是\(w\)不变
那么大胆猜测,当\(i\)小于某个值的时候,\(w\)缩小,\(i\)大于某个值的时候,\(w\)扩大,\(i\)适中时不变
然后具体来考虑,设\(dp[y][j]\)中斜率为\(0\)的段为\([L,R]\)
- 当\(i\)较小的时候,最优的策略肯定是把\(w\)改小
具体来说,当\(i<L\)时,最优策略是把\(w\)改成\(0\)
此时贡献为\(dp[y][i]+=dp[x][i]+w\),因为\(dp[x][j]\)在\(j<L\)时是单调递减的,且相邻两个点的斜率差\(\geq1\),所以当\(j\)变成\(j-1\)时,\(dp[x][j]\)增值\(\geq1\),\(|w+j-i|\)增值先为\(-1\)后为\(1\),显然\(j=i\)时最优
当\(i<L+w\)时,最优策略是取\(j=L\)
此时贡献为\(dp[y][i]+=dp[x][L]+w+L-i\),当\(j\)从\(j\)变成\(j-1\)时,\(dp[x][j]\)增值\(\geq1\),\(|w+j-i|\)增值先为\(-1\)后为\(1\),当\(j\)从\(j\)变成\(j+1\)时,\(dp[x][j]\)不变,\(|w+j-i|\)增加\(1\),若\(j\)增大到\(>R\),此时\(dp[x][j]\)增值\(\geq1\),\(|w+j-i|\)增值为\(1\)
- 当\(i\)很大的时候,最优策略就是把\(w\)尽可能扩大
具体的,当\(i>R+w\)时,最优策略就是把\(w\)尽可能扩大
此时有\(dp[y][i]+=dp[x][R]+i-w-R\),考虑\(j\)从\(j\)变成\(j+1\),此时增量\(\geq 1\),而\(|w+j-i|\)的增量一开始为\(-1\),后面为\(1\),显然\(j=R\)时最优
- \(i\)适中时,\(w\)不变
此时\(i\in[L+w,R+w]\),最优策略是\(w\)不变
此时有\(dp[y][i]+=dp[x][i-w]=dp[x][L]\),当\(j\)变成\(j-1\)时,\(|w+j-i|\)增量为\(1\),\(dp[x][j]\)的增量\(\geq0\),变成\(j+1\)同样
就此,我们严格证明了\(j\)的取值是一个分段函数,整合一下有:
\[dp[y][i]=\left\{ \begin{aligned} &dp[x][i]+w&&(i<L)\\ &dp[x][L]+w+L-i&&(L\leq i<L+w)\\ &dp[x][L]&&(L+w\leq i\leq R+w)\\ &dp[x][R]+i-w-R&&(i>R+w) \end{aligned} \right. \]考虑\(dp[y]\)对\(dp[x]\)的函数图像的影响
- \(i<L\)时,\(dp[x]\)向上平移\(w\)个单位
- \(L\leq i<L+w\)时,向上平移\(w\)个单位的同时把斜率改为\(-1\)
- \(L+w\leq i\leq R+w\)时,把原本\([L,R]\)的函数平移到\([L+w,R+w]\)来即可
- \(i>R+w\)时,把斜率修改为\(1\)
可以发现函数是连续的,所以只考虑维护函数的拐点,一个拐点代表斜率\(+1\),维护一个可重可并堆即可
\(O((N+M)\log(N+M))\)
#5979. UOJ 575 光伏元件
首先行、列拆点,\(i\)表示第\(i\)行,\(i+n\)表示第\(i\)列
先考虑如何表达\(|c_{0,i}-c_{1,i}|\leq k\)这一限制,我们假设\(t=\min(c_{0,i},c_{1,i})\),则\(c_{0,i}\leq t+k\)且\(c_{1,i}\leq t+k\),那么考虑建一条边,\((i+n,i,t,0)\),这样的话,就用\(i\)的入流表示第\(i\)行的\(1\)的个数,\(i+n\)的出流表示第\(i+n\)行的\(1\)的个数,对于拆成的两个限制,连边\((s,i,[0,k],0)\),\((i+n,t,[0,k],0)\)即可,不难发现\(t\in[l,r-k-l]\)时能恰好表示所有的情况,但此时\(t\)的含义已经不仅是\(min\)值了,这里\(k\)对\(r-l\)取\(min\)
对于\(a_{i,j}=1\),先建边\((i,j+n,[1,1],0)\),这里相当于强制让\(i\)和\(j+n\)都会分别至少有一个入流和一个出流(为什么要这么别扭的建边呢,因为我们前文提到用\(i\)的入流表示第\(i\)行\(1\)的数量,\(i+n\)的出流表示第\(i+n\)行的\(1\)的个数,那么既然我们的第一个限制条件是用\((s,i)\),\((i+n,t)\),\((i+n,i)\)这些边表示出来的,那么我们后面就不能破坏这些限制条件,具体来说,就是\(i\)不能添加新的入边,\(i+n\)不能添加新的出边),然后若这个点能修改,那么其实就相当于反悔操作,建边\((j+n,i,[0,1],c_{i,j})\)即可(因为这里相当于是反悔,也就是说,这条边是基于满足第一个限制之上的,选择这条边只是相当于去除\(i\)和\(j+n\)分别一条合法的入边和出边,去除过后的肯定也是合法的,所以此处\(i\)的入边、\(j+n\)的出边是合法的)
对于\(a_{j,i}=0\),建边\((i,j+n,[0,1],c_{i,j})\)
然后这就是一个有源汇上下界费用流了,保证有解,直接跑就行
核心就是这里对于限制关系的表达,将\(|a-b|\leq c\)变成了\(d=\min(a,b)\),\(b\leq d+c\)且\(a\leq d+c\),其它的都是基于这一步推出
另一个比较重要的就是,当我们基于某一种对于一类边的定义、建出了满足某一限制的边之后,再去做其他的限制时,不能再使用这一类边,因为会破坏这一限制,但是有一种例外,就是我们建出了这一类边的一个反边\(a\),然后再建出\(a\)的反边\(b\)(\(b\)肯定是属于这一类边的),此时若满足只有\(a\)被选中了之后,才能选中\(b\),那么这个\(b\)也是允许存在的,也就是说,\(b\)是\(a\)的反悔,此时因为选中\(a\)的时候是一定合法的,所以\(b\)将其反悔掉了过后整个局面也是合法的
E - Numbers on the blackboard
最后的答案肯定为\(\sum_{l\leq i\leq r} 2^{p_i}\times a_i\)
然后这个\(p\)满足以下限制:
- \(p_i=0\)(\(i=l\))
- \(1\leq p_i\leq p_{i-1}+1\)(\(l<i\leq r\))
以下不特别考虑\(i=1\)
那么若\(a_i>0\),那么我们肯定是希望它的\(p_i\)尽可能大也就是取\(p_{i-1}+1\),即在\(i-1\)合并到前面去之前,\(i\)就合并到\(i-1\)了
步骤一:那么先不考虑询问,我们要使得答案最大,肯定是从最右端开始向左合并,直到当前合并出来的值为负数,就停下,然后向前找,直到找到下一个为非负数的点,然后又从它开始向前合并
步骤二:那么最后就只剩下了一堆权值为负的点(也有可能只剩下一个非负的点),那么对于这些点我们希望它们的\(p_i\)尽可能小,所以现在从左往右合并,那么每个点的\(p_i\)都等于\(1\)
现在考虑能不能从左往右加点的进行步骤一,显然是可以的
假设我们已经处理好了当前已经加进来了的所有点最后缩成的负点,那么加入一个新点\(t\),若它是负数,就不管,否则就将它与目前最后一个负点融合,它的贡献就是\(2^{sz}\times a_t\),其中\(sz\)表示最后一个负点所代表的原来的点的数量
若这个负点又变成正的了,就继续向前融合
这样的话,我们就可以将询问离线,对所有询问按右端点从小到大排序,然后考虑怎么处理询问,即怎么进行步骤二
我们先加点加到\(r\),这样就不用考虑右边界,接下来考虑\(l\)
找到\(l\)所处的点,那么对于这个点之后的所有点,它们都可以用上述步骤二的方式解决,即它们的\(p_i\)都是1,对于\(l\)处于的这个点,将它拆成原来的样子,舍去\(l\)左边多余的原来的点,剩下的原来的点,因为都是这个点所代表的一个区间的点的右边部分,所以它们一定可以全部按照步骤一的方式合并
题面:
T1
有一个\(n\times m\)个点的有向分层图,共有\(n\)层,每层\(m\)个点,每条边从第\(i\)层连向\(i+1\)层,流量为\(1\)
定义\(f(i,j)\)以\(i\)层的点为起点,\(j\)层的点为终点的最大流,要求每条流的顶点和边都不交
呆猫想知道\(\sum_{i=1}^n\sum_{j=i+1}^n f(i,j)\)的值,但她太菜了,你能帮帮她吗 (;´д`)ゞ
\(n\leq40000,k\leq9\)
T2
给定一张 \(n\) 个顶点,\(m\) 条边的有向图 \(G\),其中每条边有一个非负整数的容量。其中有 \(k\) 条边是特殊的,它们在原图中的编号为 \(1\) 到 \(k\)。在初始情况下它们的容量均为\(0\)。
现在有 \(q\) 组询问,对于每组询问,会给定 \(k\) 个非负整数\(w_1, w_2, \ldots, w_k\),呆猫给你布置了一个每日委托,你需要求出:如果将编号为\(i\) 的特殊边的容量改为 \(w_i\) (对 \(i=1,2,\ldots,k\)),那么从 \(1\) 到 \(n\) 的最大流会是多少?如果你能完成这个问题,呆猫奖励你和肘鸡一起玩原神 (p≧w≦q)
\(2\le n \le10^4\) , \(1\le m \le10^4\) , $1\le k \le\min(10, m) $ , \(1\le q \le2\cdot10^5\)
\(0\le w \le25\)
T3
呆猫只需要讲题就行了,而听课的人要考虑的可就多了,为了让听课的人再多考虑点,呆猫提出了一个问题 ☆⌒(*^-゜):
给定一个长度为 \(2n-1\) 的序列 \(a\),你可以随意排列 \(a\) 中的元素,请求出有多少种不同的序列 \(b\),满足
- \(b\) 的长度为 \(n\)。
- \(b_i=\{a_1\ldots a_{2i-1}\}\) 的中位数。
\(n\leq50\)。
答案对 \(10^9+7\) 取模。
T4
为了祝贺大家已经熬过了前三题,呆猫为大家准备了肘鸡表演!*★,°*:.☆( ̄▽ ̄)/$:*.°★*
肘鸡表演是最引人注目的节日活动之一。在表演中,所有的肘鸡必须同时爆炸。为了确保安全,肘鸡被安置在远离开关的位置上,通过一些导火索与开关相连。导火索的连接方式形成一棵树,肘鸡是树叶,如图所示。火花从开关出发,沿导火索移动。每当火花抵达一个分叉点时,它会扩散到与之相连的所有导火索,继续燃烧。导火索燃烧的速度是一个固定常数。图中展示了六车肘鸡 \(\{E_1, E_2, \dots, E_6\}\) 的连线布局,以及每根导火索的长度。图中还标注了当在时刻 \(0\) 从开关点燃火花时,每一发肘鸡的爆炸时间。
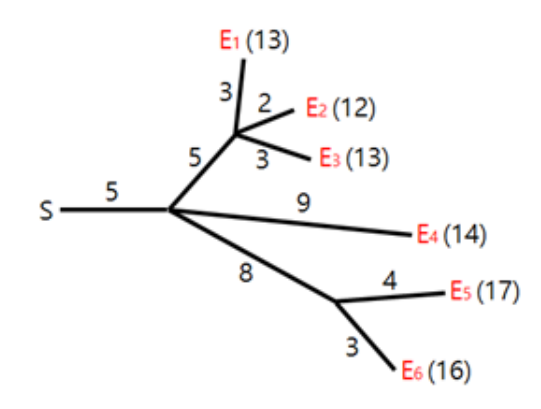
呆猫为肘鸡表演设计了导火索的连线布局。不幸的是,在她设计的布局中,肘鸡不一定同时爆炸。我们希望修改一些导火索的长度,让所有肘鸡在同一时刻爆炸。例如,为了让图中的所有肘鸡在时刻 \(13\) 爆炸,我们可以像下图中左边那样调整导火索长度。类似地,为了让图中的所有肘鸡在时刻 \(14\) 爆炸,我们可以像下图中右边那样调整长度。
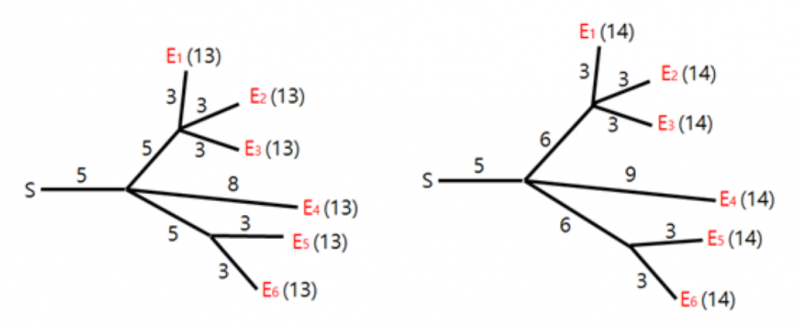
修改导火索长度的代价等于修改前后长度之差的绝对值。例如,将上面那副图中布局修改为下面那副图的左边布局的总代价为 \(6\),而修改为右边布局的总代价为 \(5\)。
导火索的长度可以被减为 \(0\),同时保持连通性不变。
呆猫想知道,至少要花费多少代价才能使得所有肘鸡在同一时刻爆炸
导火索长度\(C_i\)有(\(1\leq C_i \leq10^9\)),\(1\leq N+M \leq300000\)
T5
看完肘鸡表演,呆猫决定带你去监狱里玩玩吧!顺便探望一下典狱长 ( ̄△ ̄;)
呆猫在地图中为你选出了一片\(n\times n\)的方形监狱,这里坐落着一座肘鸡能发电站,这将会作为“\(Vegetable\ Juice\ Orange\)”实验室的专用能源。
为了保证能源供给稳定,防止机房断电惨案导致原神时间被迫中断,你被委派为发电站对接和监测工作的负责人。
你本以为只需要在米哈游逛一逛就能完成任务,驾车来到电站之后,才发现问题有本质的不同。
电站年久失修,不仅控制系统无迹可寻,旧的线路也已经全部湮没于黄沙之中。幸运地是,所有光伏元件仍然保持完好——现在,要重新排布和连接这些光伏元件使其恢复运转。
给出\(n\times n\) 的\(0/1\)矩阵\(A\),其中 \(A_{i, j}=1\) 表示位置 \((i,j)\) 有光伏元件,而 \(0\) 表示没有元件。
受新的布线方案的限制,对光伏元件的分布有下列要求:
设第 \(i\) 行的元件个数为 \(c_{0,i}\) ,第 \(i\) 列的元件个数为 \(c_{1,i}\)。
对于每个 \(i\) ,给出 \(dl_i, dr_i, k_i\) ,要求 \(\left\lvert c_{0,i}-c_{1,i} \right\rvert\leq k\) 且 \(c_{0,i}, c_{1,i}\in\left[dl_i,dr_i\right]\)。即:要求第 \(i\) 行和第 \(i\) 列的元件个数在 \(\left[dl_i, dr_i\right]\) 之间,且相差不超过 \(k_i\)。
给出 \(n\times n\) 的矩阵 \(C\),以 \(C_{i, j}\) 表示改变位置 \((i,j)\) 上元件有/无状态的代价;特别地,若 \(C_{i, j} = -1\),则表示 \((i,j)\) 位置的状态不可改变。
你深知:干活的进度一目了然,咕掉的空洞深不见底,而 \(deadline\) 总是比想象中近。于是,你计划尽快找到一组光伏元件的排布方案,在满足要求的前提下,使得总费用最小,否则你会被典狱长关进监狱!
数据保证至少存在一组解。
\(1\leq n\leq100\),\(0\leq dl_i\leq dr_i\leq n\),\(0\leq k_i\leq n\),\(C_{i,j}\geq -1\),\(\sum|C_{i,j}|\leq2e9\)
T6
呆猫编不出来背景了!所以直接看题吧 (>﹏<)
给出n个数字,每次询问一个区间$ [l,r] $ ,对这个区间内部的点进行操作。
每次操作可以合并相邻两个数 \(x\) , \(y\) ,将它们变成 $ x+2y $ 对于每次询问输出当最后只剩下一个数字时,这个数字的最大值。
有\(q\)次询问互相独立,答案对\(1e9+7\)取模。
\(1\leq n,q\leq10^5\),\(-10^9\leq a_i\leq10^9\)
标签:2024.7,一个,导火索,选讲,leq,考虑,杂题,元件,dp From: https://www.cnblogs.com/LuoyuSitfitw/p/18284588