概率与期望

标签：概率 frac int times rg 期望 dp

1 事件与概率

某些现象，在个别试验中，其结果呈现出不确定性，而在大量重复实验中其结果又具有统计规律，这些现象称为“随机事件”。

一个试验称为“随机试验”，是指它具有以下3个特点：

1.可以在相同的条件下重复进行。

2.每次试验的可能结果可以不止一个，并且能事先明确试验的所有可能结果。

3.进行一次试验前不能确定哪一个结果会出现。

某个随机试验所有可能的结果的集合称为样本空间，一般记为\(S\)。\(S\)的元素即为试验的每个结果，称为样本点。一般都假设\(S\)由有限个元素组成，\(S\)的子集称为随机事件，简称事件。在每次试验中，当且仅当这一子集中的一个样本点出现时，称这一事件发生。

随机事件是事件空间\(S\)的子集，它由事件空间\(S\)中的单位元素组成，用大写字母\(A,B,C,\cdots\)表示。
例如在掷两个骰子的随机试验中，设随机事件\(A\)为“获得的点数和大于10”，则\(A\)可以由下面3个单位事件组成：\(A = \{(5,6),(6,5),(6,6)\}\)。

1.1 事件

1.基本事件：
由一个样本点组成的单个元素的集合。

2.必然事件：
在某种条件下，一定会发生的事件，叫做相对于该条件的必然事件，简称必然事件。

3.不可能事件：
在某种条件下，一定不会发生的事件，叫做相对于该条件的不可能事件，简称不可能事件。

4.随机事件：
在某种条件下，可能发生，也可能不发生的事件，叫做相对于该条件的随机事件，简称随机事件。

1.2 频数、频率及概率

1.频数和频率：
在相同条件下重复n次试验，观察某一事件\(A\)是否发生，称n次事件中事件\(A\)出现的次数\(n_A\)为事件\(A\)的频数，称事件\(A\)出现的比例\(f_n(A) = \frac{n_A}{A}\)为事件\(A\)出现的频率。

2.概率：
对于给定的随机事件\(A\)，由于事件\(A\)发生的频率\(f_n(A)\)随着试验次数的增加稳定于某个常数上，把这个常数记作\(P(A)\)，称为事件\(A\)的概率。

3.概率的意义：

• 随机事件在一次的试验中发生与否是随机的，但随机性中含有规律性。
• 概率是频率的稳定值，是一个确定的常数。概率大，并不表示事件一定发生，只是说事件发生的可能性大。

1.3 事件的关系及运算

名称	定义	符号表示
包含关系	如果事件\(A\)发生，则事件\(B\)一定发生，这时称事件\(B\)包含事件\(A\)（或称事件\(A\)包含于事件\(B\)）	\(B \supseteq A\) \((或A \subseteq B)\)
相等关系	若\(B \supseteq A\)且\(B \subseteq A\)，那么称事件\(A\)与事件\(B\)相等	\(A = B\)
并事件（和事件）	若某事件发生当且仅当事件\(A\)或事件\(B\)发生，则称此事件为事件\(A\)与事件\(B\)的并事件（或和事件）	\(A \cup B\) \(（或A + B）\)
交事件（积事件）	若某事发生当且仅当事件\(A\)发生且事件\(B\)发生，则称此事件为事件\(A\)与事件\(B\)的交事件（或积事件）	\(A \cap B\) \((或A \times B)\)
互斥事件	若\(A \cap B\)为不可能事件，也就是\(AB\)不可能同时发生，那么称事件\(A\)与事件\(B\)互斥或互不相容	\(A \cap B = \varnothing\)
对立事件	若\(A \cap B\)为不可能事件，且\(A \cup B\)为必然事件，那么称事件\(A\)与事件\(B\)互为对立事件	\(A \cap B = \varnothing\) \(P(A \cup B) = P(A) + P(B) = 1\)

古典概率

概率依其计算方法不同，可分为古典概率、试验概率和主观概率。古典概率通常又叫事前概率，是指当随机事件中各种可能发生的结果及其出现的次数都可以由演绎或外推法得知，而无需经过任何统计试验即可计算各种结果的概率。

人们最早研究概率是从掷硬币、掷骰子等游戏中开始的。这类游戏有几个共同特点：

• 试验的样本空间有限。
• 试验中每个结果出现的可能性相同。
• 这些随机现象所能发生的事件是互不相容的。

具有这几个特点的随机试验称为古典概型或等可能概型。计算古典概型概率的方法称为概率的古典定义或古典概率。
在计算古典概率时，如果在全部可能出现的基本事件范围内，构成事件\(A\)的基本事件有\(a\)个，不构成事件\(A\)的有\(b\)个，则出现事件\(A\)的概率为\(P(A) = \frac{a}{a + b}\)。

例题1：

在40支圆珠笔中有30支是黑色的，其余10支是红色的。从中任意取出4支，计算这4支中包含至少一支红笔的概率。

解法一：
设有四个事件\(A,B,C,D\)，代表这四支笔中分别有1、2、3、4支红笔。对于每个事件的概率，计算如下所示：
\(P(A) = \frac{C_{10}^{1} \times C_{30}^{3}}{C_{40}^{4}} = \frac{40600}{91390}\)，\(P(B) = \frac{C_{10}^{2} \times C_{30}^{2}}{C_{40}^{4}} = \frac{19575}{91390}\)，\(P(C) = \frac{C_{10}^{3} \times C_{30}^{1}}{C_{40}^{4}} = \frac{3600}{91390}\)，\(P(D) = \frac{C_{10}^{4}}{C_{40}^{4}} = \frac{210}{91390}\)
于是满足题目要求的概率为：
\(P(A \cup B \cup C \cup D) = \frac{19575}{91390} + \frac{3600}{91390} + \frac{40600}{91390} + \frac{210}{91390} = \frac{63985}{91390}\)。

解法二：
我们只要求出少于一支红笔的概率，之后用1减去即可。
\(P(\complement_\Omega A) = P(\Omega) - P(A) = 1 - \frac{27405}{91390} = \frac{63985}{91390}\)。

1.4 概率的基本性质

1.任何事件的概率在\(0 \sim 1\)之间。
2.必然事件的概率为1，不可能事件的概率为0。
3.如果事件\(A\)与事件\(B\)互斥，则\(P(A\cup B) = P(A) + P(B)\)。
4.如果事件\(A\)与事件\(B\)互为对立事件，则\(A\cup B\)为必然事件，\(P(A \cup B) = 1\)，\(P(A) = 1 - P(B)\)。
5.互斥事件的可加性：设\(A_1,A_2,\cdots ,A_n\)是互斥的n个事件，则\(P(A_1\cup A_2 \cup \cdots A_n) = P(A_1) + P(A_2) + \cdots +P(A_n)\)。
6.相互独立的事件的可乘性：如果事件\(A\)是否发生对事件\(B\)发生的概率没有影响，同时事件\(B\)是否发生对事件\(A\)发生的概率也没有影响，则称\(A\)与\(B\)是相互独立事件，有\(P(A\cap B) = P(A) \times P(B)\)。推广到n个相互独立事件，\(P(A_1\cap A_2\cap \cdots A_n) = P(A_1) \times P(A_2) \times \cdots P(A_n)\)。

1.5 条件概率

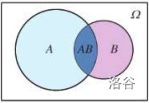
如图，若已知事件\(A\)发生，则\(A\)成为样本空间。此时，事件\(B\)发生的概率是\(AB\)包含的样本点数与\(A\)包含的样本点数的比值，即：

\(P(B|A) = \frac{n(AB)}{n(A)}\)

因为：

\(P(B|A) = \frac{n(AB)}{n(A)} = \frac{\frac{n(AB)}{n(\Omega)}}{\frac{n(A)}{n(\Omega)}} = \frac{P(AB)}{P(A)}\)

所以，在事件\(A\)发生的条件下，事件\(B\)发生的概率还可以通过\(\frac{P(AB)}{P(A)}\)来计算。
一般的，设\(A,B\)为两个随机事件，且\(P(A) > 0\)，我们称\(P(B|A) = \frac{P(AB)}{P(A)}\)为在事件\(A\)发生的条件下，事件\(B\)发生的条件概率，简称条件概率。

由条件概率的定义，对任意两个事件\(A\)和\(B\)，若\(P(A)>0\)，则：

\(\large P(AB) = P(A)P(B|A)\)

我们称上式为概率的乘法公式。

例题2：

在5道试题中有3道代数题和2道几何题，每次从中随机抽出1道题，抽出的题不在放回。求：
（1）第1次抽到代数题且第2次抽到几何题的概率；
（2）在第1次抽到代数题的条件下，第2次抽到几何题的概率。

分析：
如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件，那么问题（1）就是积事件的概率，问题（2）就是条件概率。可以先求积事件的概率，再用条件概率公式求条件概率；也可以先求条件概率，再用乘法公式求积事件的概率。

解：
设\(A = \texttt{“第1次抽到代数题”}\)，\(B = \texttt{“第2次抽到几何题”}\)。
方法一：
（1）从5道试题中不放回地随机抽取2道，试验的样本空间\(\Omega\)包含20个等可能的样本点，即\(n(\Omega) = A_{5}^{2} = 5 \times 4 = 20\)。
因为\(n(AB) = A_{3}^{1} \times A_{2}^{1} = 3 \times2 = 6\)，所以：
\(P(AB) = \frac{n(AB)}{n(\Omega)} = \frac{6}{20} = \frac{3}{10}\)。
（2）显然\(P(A) = \frac{3}{5}\)，利用条件概率公式，得：
\(P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{3}{10}}{\frac{3}{5}} = \frac{1}{2}\)
方法二：
因为\(n(A) = 3\times 4 = 12\)，\(n(AB) = 3 \times 2 = 6\)，所以：
\(P(B|A) = \frac{n(AB)}{n(A)} = \frac{6}{12} = \frac{1}{2}\)
又\(P(A) = \frac{3}{5}\)利用乘法公式可得：
\(P(AB) = P(A)P(B|A) = \frac{3}{5} \times \frac{1}{2} = \frac{3}{10}\)

条件概率只是缩小了样本空间，因此条件概率同样具有概率的性质。设\(P(A)>0\)，则：
（1）\(P(\Omega | A) = 1\)；
（2）如果\(B\)和\(C\)是两个互斥事件，则\(P(B\cup C|A) = P(B|A)+P(C|A)\)；
（3）设\(\overline B\)和\(B\)互为对立事件，则\(P(\overline B | A) = 1 - P(B|A)\)。

1.6 全概率公式

从放有a个红球和b个蓝球的袋子中，每次随即摸出1个球，摸出的球不再放回，显然，第1次摸到红球的概率为\(\frac{a}{a+b}\)，那么第2次摸到红球的概率是多大？

用\(R_i\)表示事件“第i次摸到红球”，\(B_i\)表示事件“第i次摸到蓝球”。事件\(R_2\)可按第1次可能的摸球结果表示为两个互斥事件的并，即\(R_2 = R_1R_2\cup B_1R_2\)，利用概率的加法公式和乘法公式，得：

\[\begin{aligned} P(R_2) &= P(R_1R_2\cup B_1R_2) = P(R_1R_2) + P(B_1R_2) \\ &= P(R_1)P(R_2|R_1)+P(B_1)P(R_2|B_1) \\ &= \frac{a}{a+b} \times \frac{a-1}{a+b-1}+\frac{b}{a+b}\times \frac{a}{a+b-1} \\ &= \frac{a\times (a+b-1)}{(a+b) \times (a+b-1)} \\ &= \frac{a}{a+b} \end{aligned} \]

上述过程采用的方法是：按照某种标准，将一个复杂事件表示为两个互斥事件的并，再由概率的加法公式和乘法公式求得这个复杂事件的概率。

一般地，设\(A_1,A_2,\cdots ,A_n\)是一组两两互斥的事件，\(A_1\cup A_2\cup \cdots \cup A_n = \Omega\)，且\(P(A_i)>0(1\le i \le n)\)，则对任意的事件\(B \subseteq \Omega\)，有：

\(\large P(B) = \displaystyle \sum_{i=1}^{n}P(A_i)P(B|A_i)\)

我们称上面的公式为全概率公式。

例题3：

有三台车床加工同一型号的零件，第1台加工的次品率为6%，第2，3台加工的次品率均为5%，加工出来的零件混放在一起。已知第1，2，3台车床加工的零件数分别占总数的25%，30%，45%。
（1）任取一个零件，计算它是次品的概率；
（2）如果取到的零件是次品，计算它是第i台车床加工的概率。

解：
设\(B = \text{“任取一个零件为次品”}\)，\(A_i = \text{“零件为第i台车床加工”}\)，则\(\Omega = A_1\cup A_2\cup A_3\)，且\(A_1,A_2,A_3\)两两互斥。根据题意得：
\(P(A_1) = 0.25,P(A_2) = 0.3,P(A_3)=0.45\)
\(P(B|A_1) = 0.06,P(B|A_2)=P(B|A_3)=0.05\)
（1）由全概率公式得：

\[\begin{aligned} P(B) &= P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3) \\ &= 0.25\times0.06+0.3\times0.05+0.45\times0.05 \\&= 0.0525\end{aligned} \]

（2）“如果取到的零件是次品，计算它是第i台车床加工的概率”，就是计算在\(B\)发生的条件下，事件\(A\)发生的概率。
\(P(A_1|B) = \frac{P(A_1B)}{P(B)} = \frac{P(A_1)P(B|A_1)}{P(B)} = \frac{0.25\times0.06}{0.0525}=\frac{2}{7}\)
类似地，可得：
\(P(A_2|B)=\frac{2}{7},P(A_3|B)=\frac{3}{7}\)

例题4：

来自三个地区的考生报名表分别为10份、15份、25份，其中女生报名表分别为3份、7份、5份。任取一个地区的报名表，从中无放回地先后抽取2份，试求：
（1）先抽到的1份是女生表的概率；
（2）已知后抽到的1份是男生表，求先抽到的1份是女生表的概率。

解：
记\(H_i = \text{“抽到地区考生的报名表”}，A_j=\text{“第j次抽到的报名表是男生的”}\)，则有：
\(P(H_i)=\frac{1}{3}，P(A_1|H_1)=\frac{7}{10},P(A_1|H_2)=\frac{8}{15},P(A_1|H_3)=\frac{20}{25}\)
（1）由全概率公式知：
\(p=P(\overline {A_1})=\displaystyle \sum_{i=1}^{3}P(H_i)P(\overline{A_1}|H_i)=\frac{1}{3}\times(\frac{3}{10}+\frac{7}{15}+\frac{5}{25})=\frac{29}{90}\)
（2）\(q=P(\overline{A_1}|A_2)=\frac{P(\overline{A_1}A_2)}{P(A_2)}\)，由全概率公式得：
\(P(\overline{A_1}A_2)=\displaystyle \sum_{i=1}^{3}P(H_i)P(\overline{A_1}A_2|H_i)=\frac{1}{3}\displaystyle\sum_{i=1}^{3}P(\overline{A_1}A_2|H_i)\)，又因为
\(P(\overline{A_1}A_2|H_1)=\frac{3}{10}\times\frac{7}{9}=\frac{7}{30}\)，
\(P(\overline{A_1}A_2|H_2)=\frac{7}{15}\times\frac{8}{14}=\frac{8}{30}\)，
\(P(\overline{A_1}A_2|H_2)=\frac{5}{25}\times\frac{20}{24}=\frac{5}{30}\)
所以：\(P(\overline{A_1}A_2)=\frac{1}{3}\times(\frac{7}{30}+\frac{8}{30}+\frac{5}{30})=\frac{2}{9}\)，
而

\[\begin{aligned} P(A_2) &= \sum _ {i=1} ^ {3} P(H_i)P(A_2|H_i) \\ &= \frac 1 3\sum_{i=1}^{3}P(A_2|H_i) \\ &= \frac13\times(\frac{7}{10}+\frac{8}{15}+\frac{20}{25})\\&=\frac{61}{90}\end{aligned} \]

所以\(q=\frac{P(\overline{A_1}A_2)}{P(A_2)}=\frac{\frac29}{\frac{61}{90}}=\frac{20}{61}\)。

1.7 贝叶斯定理

在例题3中，\(P(A_i)\)是试验之前就已知的概率，它是第i台车床加工的零件所占的比例，称为先验概率。当已知抽到的零件是次品（\(B\)发生），\(P(A_i|B)\)是这件次品来自第i台车床加工的可能性大小，通常称为后验概率。
将问题（2）一般化，可以得到贝叶斯公式。

贝叶斯公式：设\(A_1,A_2,\cdots,A_n\)是一组两两互斥的事件，\(A_1\cup A_2\cup \cdots \cup A_n = \Omega\)，且\(P(A_i)>0\)，则对任意的事件\(B\subseteq\Omega,P(B)>0\)，有：

\(\large P(A_i|B)=\frac{P(A_i)P(B|A_i)}{P(B)}=\frac{P(A_i)P(B|A_i)}{ \sum_{k=1}^{n}P(A_k)P(B|A_k)},i=1,2,\cdots,n\)

例题5：

在数字通信中，信号是由数字0和1组成的序列。由于随机因素的干扰，发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时，接收0和1的概率分别为0.9和0.1；发送信号1时，接收为1和0的概率分别为0.95和0.05。假设发送信号0和1是等可能的。
（1）分别求接收的信号为0和1的概率；
（2）已知接收的信号为0，求发送的信号是1的概率。

分析：
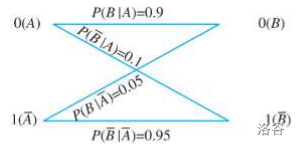
设\(A = \text{“发送的信号为0”},B=\text{“接收到的信号为0”}\)。为便于求解，我们可将题目中所包含的各种信息用下图直观表示。

解：
由题意得：\(P(A)=P(\overline A)=0.5,P(B|A)=0.9,P(\overline B|A)=0.1,P(B|\overline A)=0.05,P(\overline B|\overline A)=0.95\)
（1）\(P(B)=P(A)P(B|A)+P(\overline A)P(B|\overline A)=0.5\times0.9+0.5\times0.05=0.475\)，
\(P(\overline B)=1-P(B)=1-0.475=0.525\)
（2）\(P(\overline A|B)=\frac{P(\overline A)P(B|\overline A)}{P(B)} = \frac{0.5 \times 0.05}{0.475}=\frac{1}{19}\)

小结

1.全概率公式可以理解为：导致一个事件发生的原因有很多种（各种原因互斥），那么这个事件发生的概率就是每种原因引起该事件发生的概率的总和。

2.一个事件已经发生了且有很多原因都能导致这个事件发生，那么其中一种原因导致该事件发生的概率可以用贝叶斯公式来解决。

例题1：Codeforces 148 D Bag of mice

题目描述：

题目入口

分析：

设\(f[i][j]\)为轮到A时袋子里有i只白鼠，j只黑鼠，A赢的概率。
初始化边界：\(f[0][j]=0\)，因为没有白鼠了算B赢；\(f[i][0]=1\)，因为抓一只就是白鼠，A赢。
考虑\(f[i][j]\)的转移：

1.A抓到一只白鼠，A赢了。概率为\(\frac{i}{i+j}\)；
2.A抓到一只黑鼠，B抓到一只白鼠，B赢了。概率为\(\frac{j}{i+j}\times\frac{i}{i+j-1}\);
3.A抓到一只黑鼠，B抓到一只黑鼠，跑出来一只黑鼠，转移到\(f[i][j-3]\)。概率为\(\frac{j}{i + j}\times\frac{j-1}{i+j-1}\times\frac{j-2}{i+j-2}\)；
4.A抓到一只黑鼠，B抓到一只黑鼠，跑出来一只白鼠，转移到\(f[i-1][j-2]\)。概率为\(\frac{j}{i+j}\times\frac{j-1}{i+j-1}\times\frac{i}{i+j-2}\)。

因为求A赢的概率，第二种情况不参与计算。并且要保证后两种情况合法，所以还要判断i,j的大小，满足第三种情况至少要有3只黑鼠，满足第四种情况要有1只白鼠和2只黑鼠。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
int w, b;
double dp[1010][1010];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> w >> b;
	for (rg int i = 1; i <= w; i++) dp[i][0] = 1;
	for (rg int i = 1; i <= b; i++) dp[0][i] = 0;
	for (rg int i = 1; i <= w; i++) {
		for (rg int j = 1; j <= b; j++) {
			dp[i][j] += 1.0 * i / (i + j);
			if (j >= 3) {
				dp[i][j] += 1.0 * j / (i + j) * (j - 1) / (i + j - 1) * (j - 2) / (i + j - 2) * dp[i][j - 3];
			}
			if (i >= 1 && j >= 2) {
				dp[i][j] += 1.0 * j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2) * dp[i - 1][j - 2];
			}
		}
	}
	cout << fixed << setprecision(9) << dp[w][b] << "\n";
	return qwq;
}

例题2：POJ3071(Football)

题目描述：

有\(2^n\)支球队比赛，每次和相邻的球队踢，两两淘汰，给定任意两支球队相互踢赢的概率，求最后哪支球队最可能夺冠。即输出获胜概率最大的那支队伍编号。给定\(n\times n\)的矩阵，用来表示每支队伍间的各自胜率。输入-1为结束。

分析：

令\(dp[i][j]\)表示第i轮j赢的概率，\(p[j][k]\)表示j打败k的概率。
如果队伍j和k可能在第i轮相遇，则容易推出转移方程\(dp[i][j]=dp[i-1][j]\times dp[i-1][k]\times p[j][k]\)。
现在的难点在于如何判断j，k能不能在第i轮相遇。
从0开始标记各支战队，第m支战队第n轮会碰到的对手是 将m转化为二进制，从左往右数第n位会不同，第n+1位开始要相同，其余位任意的所有数。
转化为式子就是满足条件
\(((j>>(i-1))\land 1) == (k>>(i-1))\)
球队按\(0\sim pow(2,n)-1\)编号，可以发现两支队伍在i轮能打时，他们的二进制下右起第i位互补，之后左边全部相等。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 130;
int n;
double p[N][N], dp[8][N];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	while (cin >> n && n != -1) {
		rg int m = (1 << n);
		memset(dp, 0, sizeof(dp));
		for (rg int i = 0; i < m; i++) {
			for (rg int j = 0; j < m; j++) {
				cin >> p[i][j];
			}
		}
		for (rg int i = 0; i < m; i++) dp[0][i] = 1;
		for (rg int i = 1; i <= n; i++) {
			for (rg int j = 0; j < m; j++) {
				for (rg int k = 0; k < m; k++) {
					if (((j >> (i - 1)) ^ 1) == (k >> (i - 1))) {
						dp[i][j] += dp[i - 1][j] * dp[i - 1][k] * p[j][k];
					}
				}
			}
		}
		double op = 0;
		int ans;
		for (rg int i = 0; i < m; i++) {
			if (op < dp[n][i]) {
				op = dp[n][i];
				ans = i;
			}
		}
		cout << ans + 1 << "\n";
	}
	return qwq;
}

例题3：CF768D Jon and Orbs

题目描述：

一个人要取k种物品，一天只能取一件物品，但不能确定取到的是什么物品，求最少需要在第几天，取完这k种物品的概率不小于\(\frac{p}{2000}\)。有q组询问，每组询问给定这个p。

分析：

令\(f[i][j]\)表示前i次取出了j种的概率。于是有：
\(f[i][j] = f[i-1][j]\times\frac{j}{k}+f[i-1][j-1]\times\frac{k-j + 1}{k}\)

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 10005;
int k, q;
double f[N][1005];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> k >> q;
	f[0][0] = 1;
	for (rg int i = 1; i <= N; i++) {
		for (rg int j = 1; j <= k; j++) {
			f[i][j] = (double)f[i - 1][j] * j / k + f[i - 1][j - 1] * (k - j + 1) / k;
		}
	}
	while (q--) {
		double p;
		cin >> p;
		p = 1.0 * p / 2000;
		for (rg int i = 1; i <= N; i++) {
			if (f[i][k] > p) {
				cout << i << "\n";
				break;
			}
		}
	}
	return qwq;
}

例题4：[ABC300E] Dice Product 3

因为是求总概率，实际上每种转移的概率都是\(\frac 1 5\)，因为投到1时状态不变，不用计入。我们对所乘的数分解因数，可以发现只有2、3、5三种因数，因此如果N含有2、3、5以外的其它因数则输出0。
令\(f[i][j][k]\)表示当前数为\(2^i\times 3^j\times 5^k\)时的概率。可以发现，有\(\frac 1 5\)的概率\(\times 2\)，有\(\frac 1 5\)的概率\(\times 3\)，有\(\frac 1 5\)的概率\(\times 2^2\)，有\(\frac 1 5\)的概率\(\times 5\)，有\(\frac 1 5\)的概率\(\times 2\times 3\)。因为要求R，于是将\(\times \frac 1 5\)转化为\(\times inv(5)\)（5的逆元）。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int mod = 998244353;
ll n;
int f[61][39][27];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	rg int cnt1 = 0, cnt2 = 0, cnt3 = 0;  //分别统计2、3、5的个数 
	while (n % 2 == 0) {
		n /= 2;
		cnt1++;
	}
	while (n % 3 == 0) {
		n /= 3;
		cnt2++;
	}
	while (n % 5 == 0) {
		n /= 5;
		cnt3++;
	}
	if (n != 1) {  //如果有其它因数 
		cout << 0 << "\n";
		return qwq;
	}
	f[0][0][0] = 1;
	rg ll res = 598946612;  //即 inv(5) 
	for (rg int i = 0; i <= cnt1; i++) {
		for (rg int j = 0; j <= cnt2; j++) {
			for (rg int k = 0; k <= cnt3; k++) {
				f[i + 1][j][k] = (f[i + 1][j][k] + res * f[i][j][k] % mod) % mod;
				f[i][j + 1][k] = (f[i][j + 1][k] + res * f[i][j][k] % mod) % mod;
				f[i + 2][j][k] = (f[i + 2][j][k] + res * f[i][j][k] % mod) % mod;
				f[i][j][k + 1] = (f[i][j][k + 1] + res * f[i][j][k] % mod) % mod;
				f[i + 1][j + 1][k] = (f[i + 1][j + 1][k] + res * f[i][j][k] % mod) % mod;
			}
		}
	}
	cout << (f[cnt1][cnt2][cnt3] % mod + mod) % mod << "\n";
	return qwq;
}

2 期望

事件A有多种结果，记其结果的大小为x，那么x的期望值表示事件A的结果的平均大小，记作\(E(x)\)。
\(E(x)=\)每种结果的大小与其概率的乘积的和。
例如，记掷一枚骰子的点数为x，
\(E(x)=1\times(\frac16)+2\times(\frac16)+3\times(\frac16)+4\times(\frac16)+5\times(\frac16)+6\times(\frac16)=\frac72\)

2.1 定义

在一定区间内变量取值为有限个，或数值可以一一列举出来的变量称为离散型随机变量。一个离散型随机变量的数学期望是试验中每次可能的结果乘以其结果概率的总和。

期望值问题大多是求离散型随机变量的数学期望。如果\(X\)是一个离散的随机变量，输出值为\(x_1,x_2,\cdots\)，和输出值相应的概率分别为\(p_1,p_2,\cdots\)（概率之和为1），那么期望值是\(E(x)=\displaystyle \sum_{i}p_i\times x\)。

2.2 性质

期望的“线性”性质：
对于任意随机变量\(X\)和\(Y\)以及常量a和b，有：\(E(aX+bY)=aE(X)+bE(Y)\)。
当两个随机变量\(X\)和\(Y\)相互独立且各自都有一个已定义的期望时，有：\(E(XY)=E(X)E(Y)\)。

期望dp几种常见设转移方程数组的方法：
1.设\(f[i]\)表示的是由i状态变成最终状态的期望（由末状态逆推）
2.按题意直接设
3.把选择的东西加入数组，如\(f[i][j]\)表示第i个物品选j个的期望或\(f[i][j]\)表示有i个A物品，j个B物品的期望（结合第一种的话就是\(dp[i][j]\)表示已经有i个A，j个B离达到最终状态还差多少期望）

求转移方程：
先考虑逆向（从最终状态的解开始逆推）
如果逆向没有思路，则考虑正向。
期望dp与概率dp不同，其需要倒序求解。
当求解达到某一目标的期望花费时，由于最终的花费无从知晓（无法从无穷推起），因此期望dp需要倒序求解。
设\(f[i]\)为i状态下实现目标的期望值，即到了\(f[i]\)这个状态到目标状态的差距是多少。
初始时，令\(f[n]=0\)，即在目标状态的期望值为0，然后进行状态转移，新的状态为上一状态与转移概率的乘积再加上转移的花费，即：\(f[i-1]=f[i]\times p[i]+w[i]\)
最后初始位置\(f[0]\)即为所求的期望值。

例题1：

题目描述：

给定一个n面的骰子，问投出n个不同的面的期望投掷次数。

分析：

先考虑逆向转移，\(dp[n]=0\)表示投出n个不同的面之后，要达到投出n个不同面的状态还需要投掷0次。
即：\(dp[i]\)表示已经投出了i个面，要投出剩余n-i面的期望次数。
对于当前状态为i，投一次骰子，有\(\frac{i}{n}\)的可能投出已经出现的i个面之一，此情况下还需要投\(dp[i]\)次；有\(\frac{n-i}{n}\)的可能投出其余n-i面。此情况下还要投\(dp[i+1]\)次。
即：由于投出的面可能出现过，也可能没出现过，所以\(dp[i]\)由\(dp[i]\)与\(dp[i+1]\)转移而来。

\[\begin{aligned}dp[i]&=(dp[i]+1)\times \frac{i}{n}+(dp[i+1]+1)\times \frac{n-i}{n}\\&=dp[i]\times \frac{i}{n}+dp[i+1]\times \frac{n-i}{n}+1\end{aligned} \]

移项变成：\(dp[i]=dp[i+1]+\frac{n}{n-i}\)

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e3 + 5;
double dp[N];
int t, n;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> t;
	while (t--) {
		cin >> n;
		dp[n] = 0;
		for (rg int i = n - 1; i >= 0; i--) {
			dp[i] = dp[i + 1] + 1.0 * n / (n - i);
		}
		cout << fixed << setprecision(2) << dp[0] << "\n";
	}
	return qwq;
}

例题2：POJ 2096 Collecting Bugs

题目描述：

一个软件有s个子系统，会产生n种bug。某人一天发现一个bug，这个bug属于某种bug分类，也属于某个子系统。每个bug属于某个子系统的概率是\(\frac1s\)，属于某种bug分类的概率是\(\frac1n\)。求发现n种bug，且s个子系统都找到bug的期望天数。

分析：

设\(dp[i][j]\)表示已将找到了i种bug，并存在于j个子系统中，要达到目标状态的天数的期望。
显然，\(dp[n][s]=0\)，因为已经达到目标了。\(dp[i][j]\)状态可以转化成以下四种：
1.\(dp[i][j]\)发现一个bug属于已经找到的i种bug和j个子系统中，概率为\(\frac{i}{n}\times\frac{j}{s}\)；
2.\(dp[i+1][j]\)发现一个bug属于新的一种bug，但属于已经找到的j种子系统，概率为\(\frac{n-i}{n}\times\frac{j}{s}\)；
3.\(dp[i][j+1]\)发现一个bug属于已经找到的i种bug，但属于新的子系统，概率为\(\frac{i}{n}\times\frac{s-j}{s}\);
4.\(dp[i+1][j+1]\)发现一个bug属于新的一种bug和新的一个子系统，概率为\(\frac{n-i}{n}\times\frac{s-j}{s}\)。
又有：期望可以分解成多个子期望的加权和，权为子期望发生的概率，所以\(dp[i][j]=p_1\times dp[i][j]+p_2\times dp[i+1][j]+p_3\times dp[i][j+1]+p_4\times dp[i+1][j+1]+1\)
然后移项化简。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
int n, s;
double dp[1010][1010];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> s;
	dp[n][s] = 0;
	for (rg int i = n; i >= 0; i--) {
		for (rg int j = s; j >= 0; j--) {
			if (i == n && s == j) continue;
			dp[i][j] = (double)(dp[i + 1][j] * (n - i) * j + dp[i][j + 1] * i * (s - j) + dp[i + 1][j + 1] * (n - i) * (s - j) + n * s) / (n * s - i * j);
		}
	}
	cout << fixed << setprecision(4) << dp[0][0] << "\n";
	return qwq;
}

例题3：HDU 3853 LOOPS

题目描述：

\(R\times C\)的格子，起始点在（1，1），终点是（R，C）。走一个点需要消耗2个能量。在（i，j）时，可以以概率\(p1\)走到（i，j），以概率\(p2\)走到（i，j+1），以概率\(p3\)，走到（i+1，j）。问从起点到终点需要消耗的能量值期望。

分析：

设\(dp[i][j]\)表示从（i，j）到（R，C）所花费魔法值的期望。然后我们需要考虑这样的状态之间能否正确的转化。不难写出如下转移方程：
\(dp[i][j]=p[i][j][1]\times dp[i][j]+p[i][j][2]\times dp[i][j+1]+p[i][j][3]\times dp[i+1][j]+2\)
其中\(p[i][j][k]\)表示在（i，j）选择第k种走法的概率。
再移项化简得：
\(dp[i][j]=\frac{(p[i][j][2]\times dp[i][j+1]+p[i][j][3]\times dp[i+1][j] + 2}{1-p[i][j][1]}\)

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
int r, c;
double dp[1005][1005], p[1005][1005][3];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	while (cin >> r >> c) {
		for (rg int i = 1; i <= r; i++) {
			for (rg int j = 1; j <= c; j++) {
				cin >> p[i][j][0] >> p[i][j][1] >> p[i][j][2];
			}
		}
		memset(dp, 0, sizeof(dp));
		for (rg int i = r; i >= 1; i--) {
			for (rg int j = c; j >= 1; j--) {
				if (i == r && j == c) continue;
				if (p[i][j][0] == 1) continue;
				dp[i][j] = (double)(p[i][j][1] * dp[i][j + 1] + p[i][j][2] * dp[i + 1][j] + 2) / (1 - p[i][j][0]);
			}
		}
		cout << fixed << setprecision(3) << dp[1][1] << "\n";
	}
	return qwq;
}

例题4：P1365 WJMZBMR打osu! / Easy

题目描述：

题目入口

分析：

设\(dp[i]\)表示到了第i位的总期望，\(g[i]\)表示到了第i位结尾的连续o的期望长度，那么分情况讨论：
1.当\(s[i]==x\)，则\(dp[i]=dp[i-1],g[i]=0\)；
2.当\(s[i]==o\)，则\(dp[i]=dp[i-1]-g[i-1]^2+(g[i-1]+1)^2=dp[i-1]+2\times g[i-1]+1,g[i]=g[i-1]+1\)。
3.当\(s[i]==?\)，则\(dp[i]=dp[i-1]+\frac{(g[i-1]+1)^2-g[i-1]^2}{2}=dp[i-1]+\frac{2\times g[i-1]+1}{2},g[i]=\frac{g[i-1]+1}{2}\)
由于转移时只与上一次的状态有关，于是滚掉就好了。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 3e5 + 5;
int n;
char s[N];
double dp, g;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	cin >> s + 1;
	for (rg int i = 1; i <= n; i++) {
		if (s[i] == 'x') {
			g = 0;
		} else if (s[i] == 'o') {
			dp = (double)dp + 2 * g + 1;
			g = g + 1;
		} else {
			dp = (double)dp + (2 * g + 1) / 2;
			g = (double)(g + 1) / 2; 
		}
	}
	cout << fixed << setprecision(4) << dp << "\n";
	return qwq;
}

例题5：绿豆蛙的归宿

题目描述：

题目入口

分析：

从第一个点开始DFS，每次枚举它所连的边，并把边权加上，最后除以它的出度即可。于是：
\(dp[i]+=\frac{(dp[son[i]]+val[son[i]])}{r[i]}\)
其中\(son[i]\)表示i所连的边，\(val[i]\)是边权，\(r[i]\)是i的出度。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e5 + 5;
int n, m;
struct edge {
	int v, w;
};
vector<edge> e[N];
int r[N];
double dp[N];
bool vis[N];
inline void dfs(int u) {
	if (u == n) return ;
	if (vis[u]) return ;
	vis[u] = 1;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i].v;
		dfs(v);
		dp[u] += (double)(dp[v] + e[u][i].w) / r[u];
	}
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int u, v, w;
	for (rg int i = 1; i <= m; i++) {
		cin >> u >> v >> w;
		e[u].push_back({v, w});
		r[u]++;
	}
	dfs(1);
	cout << fixed << setprecision(2) << dp[1] << "\n";
	return qwq;
}

例题6：游走

题目描述：

题目入口

分析：

（1）考虑经过每条边的期望次数
\(g[e]=\frac{f[u]}{d[u]}+\frac{f[v]}{d[v]}\)
其中\(f[u]\)表示经过u点的期望次数，\(d[u]\)表示u点连接的边数。
（2）考虑经过每个点的期望次数
\(f[u]=\displaystyle\sum_{v\in E[u]}\frac{f[v]}{d[v]}\)
其中\(E[u]\)表示与u相连的点集。
有两个特殊的点：
第1个节点：刚开始就走过了，所以\(f[1]=1+\sum\frac{f[v]}{d[v]}\);
第n个节点：走到n就结束，任何一个点不能从n转移，所以不能将\(\frac{f[n]}{d[n]}\)计入答案，故令\(f[n]=0\)。
将（2）中的的n-1个式子看作n-1个n-1元方程组，用高斯消元求解：
第1行：\(1\times f[1]+a[1][2]\times f[2]+\cdots+a[1][n-1]\times f[n-1]=1\)
第2行：\(a[2][1]\times f[1]+1\times f[2]+\cdots+a[2][n-1]\times f[n-1]=0\)
第k行：\(a[k][1]\times f[1]+\cdots+1\times f[k]+\cdots+a[n-1][n-1]\times f[n-1]=0\)
其中a数组存的系数就是每个点的度数的倒数在取负号。
（3）根据贪心思想，期望次数多的边给它更小的编号

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 505, M = 125005;
const double eps = 1e-6;
int n, m;
int head[N], to[M << 1], nxt[M << 1], tot;
int d[N], s[M], t[M];  //点的度，边的起点、终点
double a[N][N], g[M], ans;
inline void add(int u, int v) {
	to[++tot] = v;
	nxt[tot] = head[u];
	head[u] = tot;
}
inline void gauss() {
	for (rg int i = 1; i < n; i++) {  //第i主元 
		for (rg int k = i; k < n; k++) {
			if (fabs(a[k][i]) > eps) {
				swap(a[k], a[i]);
				break;
			}
		}
		for (rg int k = 1; k < n; k++) {  //对角化 
			if (k != i) {
				for (rg int j = n; j >= i; j--) {
					a[k][j] -= a[k][i] / a[i][i] * a[i][j];
				}
			}
		}
	}
	for (rg int i = 1; i < n; i++) {
		a[i][n] /= a[i][i];  //除以主元 
	}
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	for (rg int i = 1; i <= m; i++) {
		cin >> s[i] >> t[i];
		add(s[i], t[i]);
		add(t[i], s[i]);
		d[s[i]]++;
		d[t[i]]++;
	}
	for (rg int u = 1; u < n; u++) {  //构造增广矩阵 
		for (rg int i = head[u]; i; i = nxt[i]) {
			rg int v = to[i];
			if (v != n) a[u][v] = -1.0 / d[v];  //从u走到v的概率 
		}
		a[u][u] = 1;  //f[u]移项后的系数 
	}
	a[1][n] = 1;  //f[1]的常数项
	gauss();  //点的期望次数 
	for (rg int i = 1; i <= m; i++) {
		g[i] = a[s[i]][n] / d[s[i]] + a[t[i]][n] / d[t[i]];
	}
	sort(g + 1, g + m + 1);
	for (rg int i = 1; i <= m; i++) {
		ans += g[i] * (m - i + 1);  //次数多编号小 
	}
	cout << fixed << setprecision(3) << ans << "\n";
	return qwq;
}

例题7：OSU!

题目描述：

题目描述

分析：

有：\((x+1)^3=x^3+3\times x^2+3\times x+1\)
每多增加一个1，增加了\(3\times x^2+3\times x+1\),那么用\(x1[i]\)维护\(x\)的期望，用\(x2[i]\)维护\(x^2\)的期望。
\(x1[i]=(x1[i-1]+1) \times f[i]\)；
\(x2[i]=(x2[i-1]+2\times x1[i-1]+1)\times f[i]\)；
\(dp[i]=dp[i-1]+(3\times x2[i-1]^2+3\times x1[i-1]+1)\times f[i]\)
同样可以滚掉一维。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 5;
int n;
double f, x1, x2, dp; 
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> f;
		dp = (double) dp + (3 * x2 + 3 * x1 + 1) * f;
		x2 = (double) (x2 + 2 * x1 + 1) * f;
		x1 = (double) (x1 + 1) * f;
	}
	cout << fixed << setprecision(1) << dp << "\n";
	return qwq;
}

例题8：单选错位

题目描述：

题目入口

分析：

1.当\(a_i>a_{i+1}\)时，选的数相等的范围为\(1\sim a_{i+1}\)，概率为\(\frac{a_{i+1}}{a_{i}}\times \frac{1}{a_{i+1}}=\frac{1}{a_i}\)；
2.当\(a_i<a_{i+1}\)时，选的数相等的范围为\(1\sim a_i\)，概率为\(\frac{a_i}{a_{i+1}}\times \frac{1}{a_i}=\frac{1}{a_{i+1}}\)；
3.当\(a_i=a_{i+1}\)时，选的数相等的范围为\(1\sim a_i(或a_{i+1})\)，概率为\(1\times \frac{1}{a_{i+1}}(或\frac{1}{a_i})=\frac{1}{a_{i+1}}\)。
综上，答案为\(\displaystyle \sum_{i=1}^{n}\frac{1}{max(a_i,a_{i+1})}\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e7 + 5;
int n, A, B, C;
int a[N];
double ans;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> A >> B >> C >> a[1];
	for (rg int i = 2; i <= n; i++) {
		a[i] = ((long long) a[i - 1] * A + B) % 100000001;
	}
	for (rg int i = 1; i <= n; i++) {
		a[i] = a[i] % C + 1;
	}
	a[n + 1] = a[1];
	for (rg int i = 1; i <= n; i++) {
		ans += (double) 1 / max(a[i], a[i + 1]);
	}
	cout << fixed << setprecision(3) << ans << "\n";
	return qwq;
}

例题9：Red is good

题目描述：

桌面上有R张红牌和B张黑牌，随机打乱后放在桌面上，开始一张一张地翻牌，翻到红牌得到1美元，黑牌则付出1美元。可以随时停止翻牌，在最优策略下平均能得到多少钱。

分析：

设\(dp[i][j]\)表示已经有i张红牌j张黑牌，与最终状态还剩的差距。有两种转移方式：
1.从\(dp[i-1][j]\)抽到一张红牌转移过来，概率为\(\frac{i}{i + j}\)；
2.从\(dp[i][j-1]\)抽到一张黑牌转移过来，概率为\(\frac{j}{i+j}\)。
但是会发现直接开二维数组\(MLE\)，所以滚掉一维。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5003;
int R, B;
double dp[N];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> R >> B;
	for (rg int i = 1; i <= R; i++) {
		dp[0] = i;
		for (rg int j = 1; j <= B; j++) {
			dp[j] = (double) max(0.0, (dp[j] + 1) * i / (i + j) + (dp[j - 1] - 1) * j / (i + j));
		}
	}
	int ans = dp[B] * 1000000;
	cout << ans / 1000000 << '.' << setfill('0') << setw(6) << ans % 1000000 << "\n";
	return qwq;
}

例题10：列队春游

题目描述：

题目入口

分析：

总的期望值可以用每一个小朋友的期望值加起来求得。
设k为所有身高大于等于当前小朋友的人数之和（不包括自身），然后枚举当前小朋友的视野长度L，那么在这个小朋友前面的L个位置都不能站比当前小朋友高的人，那么比小朋友高的k个人一共有\(n-L\)个位置可以放，考虑排列顺序，则共有\(A_{n-L}^{k}\)种放法。
因为视野长度为L，所以当前小朋友前面必须要预留出L个位置给比他矮的小朋友站，所以当前小朋友必须要从L+1的位置开始排，所以当前小朋友有\(n-L+1\)种站位。
根据乘法原理，符合要求的状况一共有\(A_{n-L}^{k} \times (n-L+1)\)种。
总共的情况就很好算了，就是\(A_{n}^{k+1}\)。
于是:

\[\begin{aligned} ans &= \displaystyle \sum_{L=1}^{n}\frac{(n-L+1)\ A_{n-L}^{k}}{A_{n}^{k+1}} \\ &= \displaystyle\sum_{L=1}^{n}\frac{(n-L+1)\frac{(n-L)!}{(n-L-k)!}}{\frac{n!}{(n-k-1)!}} \\ &= \frac{(n-k-1)!}{n!}\displaystyle\sum_{L=1}^{n}\frac{(n-L+1)!}{(n-L-k)!} \\ &= \frac{(n-k-1)!}{n!}(k+1)!\displaystyle\sum_{L=1}^{n}\frac{(n-L+1)!}{(n-L-k)!(k+1)!} \\ &= \frac{(n-k-1)!}{n!}(k+1)!\displaystyle\sum_{L=1}^{n}C_{n-L+1}^{k+1} \\ &= \frac{(n-k-1)!}{n!}(k+1)!C_{k+2}^{n+1} \\ &= \frac{(n-k-1)!(k+1)!}{n!}\frac{(n+1)!}{(k+2)!(n-k-1)!} \\ &= \frac{n+1}{k+2} \end{aligned}\]

对于\(\displaystyle\sum_{L=1}^{n}C_{n-L+1}^{k+1}\)化成\(C_{n+1}^{k+2}\)，由公式\(C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}\)得：

\[\begin{aligned}\displaystyle\sum_{L=1}^{n}C_{n-L+1}^{k+1}&=C_{n}^{k+1}+C_{n-1}^{k+1}+\cdots+C_{2}^{k+1}+C_{1}^{k+1} + C_{1}^{k+2}\\ &=C_{n}^{k+1}+C_{n-1}^{k+1}+\cdots+C_{2}^{k+1}+C_{2}^{k+2} \\ &\cdots \\ &= C_{n+1}^{k+2} \end{aligned}\]

然后枚举k累加即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e5 + 5;
int n;
int h[N], k[N];
double ans;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> h[i];
	}
	for (rg int i = 1; i <= n; i++) {
		for (rg int j = 1; j <= n; j++) {
			if (i != j && h[j] >= h[i]) {
				k[i]++;
			}
		}
	}
	for (rg int i = 1; i <= n; i++) {
		ans += (double) (n + 1) / (k[i] + 2);
	}
	cout << fixed << setprecision(2) << ans << "\n";
	return qwq;
}

例题11：矩形粉刷

题目描述：

题目入口

分析：

期望图上的格子数=每个格子被涂上的期望之和，而一个格子被涂上的期望=1-这个格子不被涂上的概率。
不被涂上就是指选择的两个点都在它的同一侧，于是讨论一下都在点\((i,j)\)的上方、下方、左边、右边的情况，加起来即可。
又因为四个角会重复计算，再减去。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define mi(x) (1.0 * x * x)
using namespace std;
int k, n, m;
double ans;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> k >> n >> m;
	for (rg int i = 1; i <= n; i++) {
		for (rg int j = 1; j <= m; j++) {
			double l = (j - 1) * n;  //左边
			double r = (m - j) * n;  //右边
			double u = (i - 1) * m;  //上方
			double d = (n - i) * m;  //下方
			double ul = (i - 1) * (j - 1);  //左上
			double ur = (i - 1) * (m - j);  //右上
			double dl = (n - i) * (j - 1);  //左下
			double dr = (n - i) * (m - j);  //右下
			double tot1 = (mi(l) + mi(r) + mi(u) + mi(d) - mi(ul) - mi(ur) - mi(dl) - mi(dr));
			double tot2 = mi(n * m);
			ans += 1.0 - pow(tot1 / tot2, k);
		}
	}
	cout << fixed << setprecision(0) << ans << "\n";
	return qwq;
}

例题12：守卫者的挑战

题目描述：

题目入口

分析：

\(dp[i][j][k]\)表示前i场比赛，已经赢了j场，当前背包容量是k。
当赢了这场比赛：\(dp[i][j + 1][k+a[i]] += dp[i-1][j][k]\)
当输了这场比赛：\(dp[i][j][k]+=dp[i-1][j][k]\)
因为\(k>=n\)的时候一定能把所有碎片带走，所以如果\(k>n\)，可以直接让\(k=n\)。为了防止\(k<0\)，统一让\(k+201\)，最后计算答案时只有\(k\ge 201\)的才是需要加上的。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
double dp[203][203][403], p[203];
int a[203], n, l, k;
inline int f(int x) {
	if (x > n) x = n;
	return x + 201;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> k;
	for (rg int i = 1; i <= n; i++) {
		cin >> p[i];
		p[i] /= 100;
	}
	for (rg int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	dp[0][0][f(k)] = 1;
	for (rg int i = 1; i <= n; i++) {
		for (rg int j = 0; j < i; j++) {
			for (rg int w = -(i - 1); w <= n; w++) {
				dp[i][j + 1][f(w + a[i])] += dp[i - 1][j][f(w)] * p[i];
				dp[i][j][f(w)] += dp[i - 1][j][f(w)] * (1.0 - p[i]);
			}
		}
	}
	double ans = 0;
	for (rg int i = l; i <= n; i++) {
		for (rg int j = 0; j <= n; j++) {
			ans += dp[n][i][f(j)];
		}
	}
	cout << fixed << setprecision(6) << ans << "\n";
	return qwq;
}

例题13：聪聪与可可

题目描述：

题目描述

分析：

设\(f[i][j]\)表示聪聪在i点，可可在j点，聪聪抓到可可的期望时间。
首先，聪聪每次走到的点都是固定的，因此我们可以把它预处理出来。
设\(step[i][j]\)表示当可可在j位置聪聪在i位置时聪聪的选择。我们可以直接枚举每个点，当成可可的位置进行\(BFS\)，然后就能求得\(step\)数组。
若是聪聪已经和可可在同一个位置，说明已经抓到，此时的期望为0。如果聪聪能在两部内抓到可可，只需要经过1个单位时间，此时的期望为1。
如果聪聪不能在两步内抓到可可，那么我们枚举可可走过的每种可能，和聪聪走到的位置一起进入下一状态，求得每个状态的权值。
最后根据期望的定义我们知道它将会乘可可做出的每种选择的概率，我们选择在最后除以选择的总数。
我们在输入时统计每个点的出度，而可可还可以原地不动，则出度加1即为选择的总数。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2005;
const double eps = 1e-7;
vector<int> e[N];
int n, m, st, en;
int out[N], dis[N], vis[N], step[N][N];
double f[N][N];
queue<int> q;
inline void Get_Step(int x) {
	memset(vis, 0, sizeof(vis));
	memset(dis, 127, sizeof(dis));
	q.push(x);
	vis[x] = 1;
	dis[x] = 0;
	while (!q.empty()) {
		rg int u = q.front();
		vis[u] = 0;
		for (rg int i = 0; i < e[u].size(); i++) {
			rg int v = e[u][i];
			if(!vis[v] && dis[v] > dis[u] + 1) {
				dis[v] = dis[u] + 1;
				step[v][x] = u;
				q.push(v);
				vis[v] = 1;
			} else if (dis[v] == dis[u] + 1) {
				if (u < step[v][x]) step[v][x] = u;
			}
		}
		q.pop();
	}
}
inline double dfs(int x, int y) {
	if (x == y) return 0.0;
	if (step[x][y] == y || step[step[x][y]][y] == y) return 1.0;
	if (!(fabs(f[x][y]) < eps)) return f[x][y];
	double sum = dfs(step[step[x][y]][y], y);
	for (rg int i = 0; i < e[y].size(); i++) {
		rg int v = e[y][i];
		sum += dfs(step[step[x][y]][y], v);
	}
	return f[x][y] = sum / (out[y] + 1.0) + 1.0;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	cin >> st >> en;
	int u, v;
	for (rg int i = 1; i <= m; i++) {
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
		out[u]++;
		out[v]++;
	}
	for (rg int i = 1; i <= n; i++) {
		Get_Step(i);
	}
	cout << fixed << setprecision(3) << dfs(st, en) << "\n";
	return qwq;
}

例题14：卡牌游戏

题目描述：

题目入口

分析：

如果情况A有m的概率发生，且它有n的概率直接转换成情况B，那么情况B发生的概率可加上\(m\times n\)。
概率是一层层继承，可以考虑用DP。

这道题如果使用顺序递推，第一个人有\(\frac1m\)的概率选择某一张牌，所以下一个状态出现的概率为\(\frac1m\)。但下一个状态除了包括概率值，还包括谁被淘汰了，后者也会影响接下来的结果，不好实现。

于是考虑倒序逆推，从环内人数只有1的状态开始。

模拟一下样例1。

现在卡牌给定了，上面写着\(2,3,5,7,11\)。
当环内只有1个人时，这个人已经赢了，胜率\(100\%\)。

当环内有两个人时，庄家可以从5张牌中任意选择1个，每张牌被选中的概率都是\(\frac13\)。
如果选2，淘汰对方，自己胜利。
如果选\(3,5,7,11\)，可算出他淘汰了自己，留下了第二个人。
可见，余留两个人时，庄家胜率\(20\%\)，另一人胜率\(80\%\)。

当环内有三个人时，庄家有\(\frac15\)的概率选2，结果是第2个人遭到了淘汰，剩下的\(3,1\)两人就组成了两人环的情况。
若庄家选择牌2，则2号被淘汰（不会得到胜率贡献），3号（成为两人环的庄主）的胜率就是\(20\%\)，1号（成为两人环的小二）的胜率就是\(80\%\)。
但这样分配的前提是“本轮庄家选择2”，实际概率仅为\(\frac15\)，所以对3号胜利的真正贡献是\(\frac15 \times 20\%\),对1号胜利的贡献是\(\frac15\times 80\%\)。
庄家还可能选择别的牌。但是淘汰掉三人中的一人后，接下来的两人形成新环，所以可以直接从两人环的情况继承。

四人成环的情况，同样枚举庄家选择了什么牌，被淘汰的人之后的三个人的情况就可以利用已求出的三人环了。

//在第四层内，我们将根据已求出的三人环求出四人环内每个人的胜利几率
//下面所有“4”是第四层的意思，用于模拟当前层。
//a[]存储牌上的数字
for (rg int k = 1; k <= m; k++) {
	rg int p = (a[k] % 4 == 0) ? 4 : a[k] % 4;
	//取a[k]这张牌，淘汰掉 p，那么下一轮 p+1坐庄，p+2将是二号
	//因此 p+1获得“下一盘庄主的概率 * 1/m”，p+2获得“下一盘小二的概率 * 1/m”...
	for (rg itn j = 1; j <= 4 - 1; j++) {  //被淘汰者后面的3个人就成为新3人环的第1、2、3个人，因此可以获得一些胜率
		p++;  //后面一个人
		if (p > 4) {  //回到环首了 
			p = 1;
		}
		f[4][p] += (double) f[4 - 1][j] / m;  //根据上一层状态继承。本层第p个对应上一层第j个，注意这一选择的实际发生几率只有1/m
	} 
}

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
int n, m;
int a[53];
double f[53][53];  //f[i][j]表示i个人形成的环中，第j个人的胜率 
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	for (rg int i = 1; i <= m; i++) {
		cin >> a[i];
	}
	f[1][1] = 1.0;
	for (rg int i = 2; i <= n; i++) {  //根据i-1人环求出i人环的情况 
		for (rg int k = 1; k <= m; k++) {  //枚举本轮庄家选择的牌 
			rg int p = (a[k] % i == 0) ? i : a[k] % i;
			for (rg int j = 1; j <= i - 1; j++) {
				p++;
				if (p > i) p = 1;
				f[i][p] += (double) f[i - 1][j] / m;
			}
		}
	}
	for (rg int i = 1; i <= n; i++) {
		cout << fixed << setprecision(2) << f[n][i] * 100.0 << "% ";
	}
	return qwq;
}

例题15：换教室

题目描述：

题目入口

分析：

令\(dp[i][j][k]\)表示走完前i个教室，换了j次的最优方案，k表示第i个教室有没有换。

先考虑不换的情况，即\(k=0\)时的情况：
\(C1=c[i-1],C2=d[i-1],C3=c[i],C4=d[i]\)
\(mp[i][j]\)表示\(i,j\)间的最短路。
\(dp[i][j][0]=min\begin{cases}dp[i-1][j][0]+mp[C1][C3]\\dp[i-1][j][1]+mp[C1][C3]\times(1-k[i-1])+mp[C2][C3]\times k[i-1]\end{cases}\)
显然如果i-1时没有换教室，那么i-1到i只有一种情况就是都不换教室；如果i-1时换教室了那么就有两种情况：i-1换成功了，或者没换成功，所以就是对应的路径长乘上对应的概率。

\(dp[i][j][1]=min\begin{cases}dp[i-1][j-1][0]+mp[C1][C3]\times(1-k[i])+mp[C1][C4]\times k[i] \\ dp[i-1][j-1][1]+mp[C2][C4]\times k[i]\times k[i-1]+mp[C2][C3]\times k[i-1]\times\\ (1-k[i])+mp[C1][C4]\times(1-k[i-1])\times k[i]+mp[C1][C3]\times\\(1-k[i-1])\times(1-k[i])\end{cases}\)

有上面的经验对于\(k=1\)的情况也很好理解了，显然对于i-1可以是\(k=0||k=1\)，对于\(k=0\)那么就有两种情况，\(k=1\)就有四种情况。

对于这道题我们需要预处理出两点之间的最短路。因为只有300个点所以选择\(Floyd\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2003;
const double inf = 1e17 + 5;
int n, m, v, e, c[N][2], mp[303][303];
double k[N], dp[N][N][2], ans;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	memset(mp, 63, sizeof(mp));
	cin >> n >> m >> v >> e;
	for (rg int i = 1; i <= n; i++) cin >> c[i][0];
	for (rg int i = 1; i <= n; i++) cin >> c[i][1];
	for (rg int i = 1; i <= n; i++) cin >> k[i];
	for (rg int i = 1; i <= e; i++) {
		rg int x, y, w;
		cin >> x >> y >> w;
		mp[x][y] = mp[y][x] = min(mp[x][y], w);
	}
	for (rg int k = 1; k <= v; k++) {
		for (rg int i = 1; i <= v; i++) {
			for (rg int j = 1; j <= v; j++) {
				mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]);
			}
		}
	}
	for (rg int i = 1; i <= v; i++) mp[i][i] = mp[i][0] = mp[0][i] = 0;
	for (rg int i = 0; i <= n; i++) {
		for (rg int j = 0; j <= m; j++) dp[i][j][0] = dp[i][j][1] = inf;
	}
	dp[1][0][0] = dp[1][1][1] = 0;
	for (rg int i = 2; i <= n; i++) {
		dp[i][0][0] = dp[i - 1][0][0] + mp[c[i - 1][0]][c[i][0]];
		for (rg int j = 1; j <= min(i, m); j++) {
			rg int C1 = c[i - 1][0], C2 = c[i - 1][1], C3 = c[i][0], C4 = c[i][1];
			dp[i][j][0] = min(dp[i][j][0], min(dp[i - 1][j][0] + mp[C1][C3], dp[i - 1][j][1] + mp[C1][C3] * (1 - k[i - 1]) + mp[C2][C3] * k[i - 1]));
			dp[i][j][1] = min(dp[i][j][1], min(dp[i - 1][j - 1][0] + mp[C1][C3] * (1 - k[i]) + mp[C1][C4] * k[i], dp[i - 1][j - 1][1] + mp[C2][C4] * k[i] * k[i - 1] + mp[C2][C3] * k[i - 1] * (1 - k[i]) + mp[C1][C4] * (1 - k[i - 1]) * k[i] + mp[C1][C3] * (1 - k[i - 1]) * (1 - k[i])));
		}
	}
	ans = inf;
	for (rg int i = 0; i <= m; i++) {
		ans = min(ans, min(dp[n][i][0], dp[n][i][1]));
	}
	cout << fixed << setprecision(2) << ans << "\n";
	return qwq;
}

例题16：奖励关

题目描述：

题目入口

分析：

很明显是一道状压题。
如果从前往后转移，会发现问题不满足最优子结构（比如选择一个\(p_i\)为负的物品当前看起来不优，实际上却能增加之后的期望得分），当前选择具有后效性。因此我们无法确定当前的最优策略，不能从前往后dp。
不过如果我们知道了第i+1轮下，持有物品集合S的结果，我们就能确定第i轮的最优策略了。于是我们可以从后往前dp，具体的：
设\(dp[i][S]\)表示当前还剩i轮，持有物品集合为S在最优策略下的未来的期望收益。
首先枚举剩余轮数i和物品状态S，然后枚举此轮抛出n种物品的不同情况转移。
当枚举到第j个物品时，分类讨论：
（1）如果j的前提集合不被满足，拿不了，取\(dp[i-1][S]\)。
（2）如果j的前提集合被满足，根据\(p_j\)分类：
1.若\(p_j\ge 0\)就直接拿，取\(p_j+dp[i-1][S|j]\)。
2.若\(p_j<0\)就去比较还剩i-1轮时，取\(max(p_j+dp[i-1][S|j], dp[i-1][S])\),分别表示：选择物品j接受代价\(p_j\)使下一轮物品集合\(S'=S|j\)，和不选物品j下一轮物品集合仍为S。
综上，转移式为：

\[dp[i][S]=\frac1n\displaystyle\sum_{j=1}^{n}\begin{cases}dp[i-1][S]&R_j\nsubseteq S \\ p_j+dp[i-1][S|j]&R_j\subseteq S \wedge p_j\ge0\\max(p_j+dp[i-1][S|j],dp[i-1][S])&R_j\subseteq S\wedge p_j<0\end{cases} \]

实现时第2、3个转移可以合并，因为\(p_j\ge0\)时，一定有\(p_j+dp[i-1][S|j]\ge dp[i-1][S]\)。
可以滚动数组优化，但没有必要。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 16, K = 105;
int k, n;
int p[N], R[N];
double dp[K][1 << 15];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> k >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> p[i];
		rg int r;
		while (cin >> r && r) {
			R[i] |= 1 << (r - 1);
		}
	}
	for (rg int i = 1; i <= k; i++) {
		for (rg int s = 0; s < (1 << 15); s++) {
			for (rg int j = 1; j <= n; j++) {
				if ((R[j] & s) != R[j]) dp[i][s] += dp[i - 1][s];
				else dp[i][s] += max(dp[i - 1][s], p[j] + dp[i - 1][s | (1 << (j - 1))]);
			}
			dp[i][s] /= 1.0 * n;
		}
	}
	cout << fixed << setprecision(6) << dp[k][0] << "\n";
	return qwq;
}

例题17：概率充电器

题目描述：

题目入口

分析：

一道树形dp+概率。
首先每个点的贡献都是1，所以我们要求的期望就是概率，即求\(\displaystyle\sum_{i=1}^{n}P_i\)
其中\(P_i\)为i点通电的概率。
显然i通电有三种可能：
1.它自己来电了；
2.它的子树里有一个点来电了传了过来；
3.它的子树外面有一个点来电了传了过来。
设\(dp[i]\)表示第i个点通电的概率，之后我们在第一遍dfs的过程中用\(dp[i]\)表示i通电的概率，且电来自它自己或它的子树（对用第一第二种情况），在第二遍dfs时被更新为电来自于任何地方的概率（对应所有情况）。
最开始初始化，\(dp[i]=q[i]/100\)。
之后第一遍dfs，我们要将子树的信息合并给根。根通电还是有两种可能：
1.根自己来电了；
2.儿子来电，儿子通向根的边导电。
显然这两种情况只需要满足一种就够了，即求两个事件A，B的并事件的概率。
所以我们合并子树的信息的时候，\(P(A)=dp[i],P(B)=dp[j]\times p(i,j)\)，i是子树的根，j是i的儿子，p(i,j)是这条边导电的概率。
所以\(dp[i]=P(A)+P(B)-P(A)\times P(B)\)。
之后考虑第二遍dfs。一个节点有电也可能来自它的父亲，于是我们用父亲更新儿子。显然，我们只能用其他点来电传到父亲的概率来更新。
于是我们设\(P(B)=dp[j]\times p(i,j)\)，而且有：\(P(A)+P(B)-P(A)\times P(B)=dp[i]\)。
我们要求的是\(P(A)\)，即除了j这棵子树外其他点来电使得i有电的概率。
于是解一下这个方程：

\[\begin{aligned}P(A)-P(A)\times P(B)&=dp[i]-P(B)\\P(A)\times(1-P(B))&=dp[i]-P(B)\\P(A)&=\frac{dp[i]-P(B)}{1-P(B)}\end{aligned} \]

而之后我们去更新儿子的话还有一边是否导电需要考虑，于是：\(dp[j]=dp[j]+(P(A)\times p(i,j))-dp[j]\times P(A)\times p(i,j)\)。
有一个坑点就是如果\(P(B)=dp[j]\times p(i,j)=1\)，那么除以\(1-P(B)\)肯定会出错。由于\(dp[j]\)已经是1了，显然没有必要去更新它了，于是可以直接跳过这一层往下更新就好了。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e5 + 5;
const double eps = 1e-8;
int n;
double ans;
double q[N], dp[N];
struct edge {
	int to;
	double p;
};
vector<edge> e[N];
inline void dfs1(int u, int fath) {
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i].to;
		rg double p = e[u][i].p;
		if (v == fath) continue;
		dfs1(v, u);
		rg double k = dp[v] * p;
		dp[u] += (1 - dp[u]) * dp[v] * p;
	}
}
inline bool check(double a, double b) {
	if (fabs(a - b) < eps) return 1;
	return 0; 
}
inline void dfs2(int u, int fath) {
	ans += dp[u];
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i].to;
		rg double p = e[u][i].p;
		if (v == fath) continue;
		if (check(dp[v] * p, 1)) {
			dfs2(v, u);
			continue;
		}
		rg double k = (dp[u] - dp[v] * p) / (1 - dp[v] * p);
		k *= p;
		dp[v] += (1 - dp[v]) * k;
		dfs2(v, u);
	}
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (rg int i = 1; i < n; i++) {
		rg int a, b;
		rg double p;
		cin >> a >> b >> p;
		e[a].push_back({b, p / 100.0});
		e[b].push_back({a, p / 100.0});
	}
	for (rg int i = 1; i <= n; i++) {
		cin >> q[i];
		dp[i] = q[i] / 100.0;
	}
	dfs1(1, 0);
	dfs2(1, 0);
	cout << fixed << setprecision(6) << ans << "\n";
	return qwq;
}

例题18：XOR和路径

题目描述：

题目入口

分析：

设\(dp[i]\)表示节点i到n的路径异或和的期望，有：
\(dp[i]=\frac1{deg[i]}\displaystyle\sum(dp[p]\wedge w)\)
因为期望是线性的，因此每一位上的贡献之和就是答案。于是把每个边权拆开，对每一位分别进行处理。
设\(dp[i]\)表示从节点i到节点n的路径异或和的这一位上的值为1的期望。之所以是值为1的原因是在最后转十进制时若该位是0则不产生贡献。（想了好久）
于是我们发现：
（1）若从p到i的边权为1，那么走到p点的异或和的这一位必须为0。所以p对i的贡献为\(\frac{1-dp[p]}{deg[i]}\)
（2）若从p到i的边权为0，那么走到p点的异或和的这一位必须为1.所以p对i的贡献值为\(\frac{dp[p]}{deg[i]}\)
综上，\(dp[i]=\frac{1}{deg[i]}\displaystyle(\sum_{w(i,p)=0}dp[p]+\sum_{w(i,p)=1}(1-dp[p]))\)
移项得：
\(dp[i]\times deg[i]-\displaystyle\sum_{w(i,p)=0}dp[p]+\sum_{w(i,p)=1}dp[p]=\sum_{w(i,p)=0}1\)
然后使用高斯消元求解。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 105;
const double eps = 1e-8;
int n, m;
int deg[N];
double a[105][105];
struct edge {
	int to, p;
};
vector<edge> e[N];
inline void Gauss(int n) {
	for (rg int i = 1; i <= n; i++) {
		rg int t = 0;
		for (rg int j = i; j <= n; j++) {
			if (a[j][i] != 0) {
				t = j;
				break;
			}
		}
		swap(a[i], a[t]);
		rg double T = 1.0 / a[i][i];
		for (rg int j = i + 1; j <= n + 1; j++) {
			a[i][j] *= T;
		}
		a[i][i] = 1;
		for (rg int j = 1; j <= n; j++) {
			if (i != j) {
				T = a[j][i];
				a[j][i] = 0;
				for (rg int k = i + 1; k <= n + 1; k++) {
					a[j][k] -= T * a[i][k];
				} 
			}
		}
	}
}
double ans;
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	for (rg int i = 1; i <= m; i++) {
		rg int u, v, w;
		cin >> u >> v >> w;
		e[u].push_back({v, w});
		deg[u]++;
		if (u != v) {
			e[v].push_back({u, w});
			deg[v]++;
		}
	}
	for (rg int k = 30; k >= 0; k--) {  //枚举边权二进制下的第k位 
		memset(a, 0, sizeof(a));
		for (rg int u = 1; u < n; u++) {
			a[u][u] = -deg[u];
			for (rg int i = 0; i < e[u].size(); i++) {
				rg int v = e[u][i].to, w = (e[u][i].p >> k) & 1;
				if (w) {
					a[u][v] -= 1.0;
					a[u][n + 1] -= 1.0;
				} else {
					a[u][v] += 1.0;
				}
			}
		}
		a[n][n] = 1.0;
		Gauss(n);
		ans += (1 << k) * a[1][n + 1];
	}
	cout << fixed << setprecision(3) << ans << "\n";
	return qwq;
}

例题19：分手是祝愿

题目描述：

题目入口

分析：

可以发现，每个按键都不能被其他按键的组合键替代，于是我们可以从大到小遇到亮的就按来找到所有必须要按的键，这样我们就可以dp了。我们设\(dp[i]\)表示从i个需要按的键到i-1个需要按的键的期望操作次数。状态转移方程为：
\(dp[i]=\frac in+\frac{n-i}{n}\times(dp[i]+dp[i+1]+1)\)
意思是：有\(\frac{i}{n}\)的概率可以按到正确的键位，有\(\frac{n-i}{n}\)的概率按到错误的位置，所以在之后的操作中需要将这个按键按回来，所以就多了一个需要按的键，按回来i之后还是需要\(dp[i]\)的操作次数来达到i-1。移项化简得：
\(dp[i]=\frac{n+(n-i)\times dp[i+1]}{i}\)
求出之后我们先比较一下必须按的按键个数（设为cnt）和k，如果cnt更小，直接将\(dp[cnt]\)作为答案；如果k更小，求出\(dp[cnt]+dp[cnt-1]+\cdots+dp[k+1]\)的和作为答案，即从cnt到k的期望次数。最后加上一个k，乘上n的阶乘即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 5, mod = 100003;
typedef long long ll;
int n, k, cnt;
int a[N];
ll dp[N];
inline ll qpow(ll a, int b) {
	rg ll res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> k;
	for (rg int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (rg int i = n; i >= 1; i--) {
		if (a[i]) {
			cnt++;
			for (rg int j = 1; j * j <= i; j++) {
				if (i % j == 0) {
					a[j] ^= 1;
					if (j * j != i) a[i / j] ^= 1;
				}
			}
		}
	}
	for (rg int i = n; i >= k; i--) {
		dp[i] = (n + 1ll * (n - i) * dp[i + 1] % mod) % mod * qpow(i, mod - 2);
	}
	ll ans = 0;
	if (cnt <= k) {
		ans = cnt;
	} else {
		for (rg int i = k + 1; i <= cnt; i++) {
			ans = (ans + dp[i]) % mod;
		}
		ans += k;
	}
	ans %= mod;
	for (rg int i = 1; i <= n; i++) {
		ans = 1ll * ans * i % mod;
	}
	cout << ans << "\n"; 
	return qwq;
}

例题20：硬币游戏

题目描述：

题目入口

分析：

设两个人的串分别是\(A,B\)，假设当前游戏还没结束，且字符串为S，我们知道如果直接在S后面加上一个A游戏一定能结束，但是可能会出现在中途结束游戏的情况。

例：\(A=101,B=110\)

• 如果当前S以10结尾，那么加入第一个1的时候就直接结束，第一个人获胜，多加了01；
• 如果当前S以1结尾，那么加入10时结束，第二个人获胜，多加了1；
• 其余情况，第一个人获胜。
  于是可以得到一个等式：\(S101=S'A01+S''B1+SA\)，就有\(S\times\frac18=A\times\frac14+B\times\frac12+A\)。
  这个式子的来源是，每个形如\(S101\)的字符串都可以不重不漏的分解成三种不同的类型，于是这些字符串出现的概率必然相同。
  再来看直接在S后面加上一个B的情况，同样能够得到\(S110=S'A10+B\)，于是就有\(S\times\frac18=A\times\frac14+B\)。
  通过上述两个式子我们是能够知晓A，B之间的关系的，但是并不方便我们直接得出结果。
  我们还知道，一定有\(P_A+P_B=1\)，所以能够得到一个三元一次方程组：

\[\begin{cases}A+B=1\\S=10A+4B\\S=2A+8B\end{cases} \]

解得:

\[\begin{cases}S=6\\A=\frac13\\B=\frac23\end{cases} \]

于是在这种情况下，我们就得出了两人获胜的概率。
总结一下不难得出，当我们考虑加A串的时候，能够对式子产生贡献的情况是A串的一个前缀 和x串（可能是A或B）的一个后缀发生了重合，假设重合部分的长度为L，那么式子右边就会多上\(x\times\frac{1}{2^{m-L}}\)，因为剩下还有\(m-L\)长度的串可以加进去。
于是我们就可以得出一个标准化的式子：
\(S\times\frac{1}{2^m}=\displaystyle\sum_{pre(A,L)=suf(A,L)}A\times\frac{1}{2^{m-L}}+\displaystyle\sum_{pre(A,L)=suf(B,L)}B\times\frac1{2^{m-L}}\)
对加B串的情况，也能得到类似的结果，于是我们通过枚举L判断对应前后缀是否相同，并手工计算这两个方程里A和B的系数，就能算出\(A,B\)之间的比值，从而求解。

推广到任意n：
设\(pre(i,L)\)表示第i个字符串长度为L的前缀，\(suf(i,L)\)同理，那么根据之前的结论，可以推出方程组的第i个式子为：
\(S\times\frac1{2^m}=\displaystyle\sum_{j=1}^{n}\sum_{pre(i,L)=suf(j,L)}P[j]\times\frac1{2^{m-L}}\)
再结合式子\(\displaystyle\sum_{i=1}^{n}P[i]=1\)，即可联立方程组高斯消元求解。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
#define ull unsigned long long
using namespace std;
const int N = 305;
const ll base = 131;
int n, m, pre[N][N], suf[N][N];
double a[N][N], p[N], T;
char s[N];
inline void Gauss(int n) {
	for (rg int i = 1; i <= n; i++) {
		rg int t = 0;
		for (rg int j = i; j <= n; j++) {
			if (a[j][i] != 0) {
				t = j;
				break;
			}
		}
		swap(a[i], a[t]);
		T = 1.0 / a[i][i];
		for (rg int j = i + 1; j <= n + 1; j++) {
			a[i][j] *= T;
		}
		a[i][i] = 1;
		for (rg int j = 1; j <= n; j++) {
			if (i != j) {
				T = a[j][i];
				a[j][i] = 0;
				for (rg int k = i + 1; k <= n + 1; k++) {
					a[j][k] -= T * a[i][k];
				}
			}
		}
	}
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	for (rg int i = 0; i < N; i++) p[i] = pow(0.5, i);
	cin >> n >> m;
	for (rg int i = 1; i <= n; i++) {
		cin >> s + 1;
		for (rg int j = 1; j <= m; j++) {
			pre[i][j] = base * pre[i][j - 1] + s[j] - 'A';
		}
		for (rg ll j = 1, k = 1; j <= m; j++, k *= base) {
			suf[i][j] = k * (s[m - j + 1] - 'A') + suf[i][j - 1];
		}
		a[i][n + 1] = -p[m];  //可以将系数改成任意数字 
		a[n + 1][i] = 1;
	}
	a[n + 1][n + 2] = 1;
	for (rg int i = 1; i <= n; i++) {
		for (rg int j = 1; j <= n; j++) {
			for (rg int L = 1; L <= m; L++) {
				if (pre[i][L] == suf[j][L]) a[i][j] += p[m - L];
			}
		}
	}
	Gauss(n + 1);
	for (rg int i = 1; i <= n; i++) {
		cout << fixed << setprecision(10) << a[i][n + 2] << "\n";
	}
	return qwq;
}

例题21：树

题目描述：

题目入口

分析：

从u到v的路径可以分成两段：从u到lca和从lca到u。
设\(f[u]\)表示从u到\(fa[u]\)的期望步数，\(g[u]\)表示从\(fa[u]\)到u的期望步数。
可以得到：
\(f[u]=\frac{1}{deg[u]}+\displaystyle\sum_{x\in child[u]}\frac{1+f[x]+f[u]}{deg[u]}\)
\(g[u]=\frac{1}{deg[fa[u]]}+\frac{1+g[u]+g[fa[u]]}{deg[fa[u]]}+\displaystyle\sum_{x\in child[fa[u]]\wedge x\ne u}\frac{1+g[u]+f[x]}{deg[fa[u]]}\)
化简得：
\(f[u]=\sum f[x]+deg[u]\)
\(g[u]=g[fa[u]]+\sum f[x]+deg[fa[u]]\)
通过两遍dfs我们就能求出f和g数组了。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const ll mod = 1e9 + 7;
const int N = 1e5 + 5;
vector<int> e[N];
int n, q;
int deep[N], fa[N][20];
ll f[N], g[N];
inline void dfs1(int u, int fath) {
	fa[u][0] = fath;
	f[u] = e[u].size() % mod;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (v == fath) continue;
		dfs1(v, u);
		f[u] = (f[u] + f[v]) % mod;
	}
}
inline void dfs2(int u, int fath) {
	ll sum = 0;
	g[u] = (g[u] + g[fa[u][0]] + e[fa[u][0]].size()) % mod;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (v == fath) continue;
		sum = (sum + f[v]) % mod;
	}
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (v == fath) continue;
		g[v] = ((sum - f[v]) % mod + mod) % mod;
		dfs2(v, u);
	}
}
inline void dfs3(int u, int fath, int dep) {
	deep[u] = dep;
	f[u] = (f[fath] + f[u]) % mod;
	g[u] = (g[fath] + g[u]) % mod;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (v == fath) continue;
		dfs3(v, u, dep + 1);
	}
}
inline void init() {
	for (rg int i = 1; i <= 19; i++) {
		for (rg int j = 1; j <= n; j++) {
			fa[j][i] = fa[fa[j][i - 1]][i - 1];
		}
	}
}
inline int LCA(int u, int v) {
	if (deep[u] < deep[v]) swap(u, v);
	for (rg int i = 19; i >= 0; i--) {
		if (deep[fa[u][i]] >= deep[v]) {
			u = fa[u][i];
		}
	}
	if (u == v) return u;
	for (rg int i = 19; i >= 0; i--) {
		if (fa[u][i] != fa[v][i]) {
			u = fa[u][i];
			v = fa[v][i];
		}
	}
	return fa[u][0];
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> q;
	for (rg int i = 1; i < n; i++) {
		rg int u, v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs1(1, 0);
	f[1] = 0;
	g[1] = 0;
	dfs2(1, 0);
	dfs3(1, 0, 0);
	init();
	for (rg int i = 1; i <= q; i++) {
		rg int u, v;
		cin >> u >> v;
		rg int lca = LCA(u, v);
		ll ans = (f[u] - f[lca] + g[v] - g[lca] + mod) % mod;
		cout << ans << "\n";
	}
	return qwq;
}

例题22：[MtOI2019] 小铃的烦恼

首先可以发现，这道题其实与字母本身以及具体位置无关，只和各字母的个数有关。对于一种颜色\(a\)，若我们求出将所有字母染成颜色a的概率及期望步数，我们就可以求出答案。具体地，答案为\(\sum E(a)\times P(a)\)。
我们设\(P(x)\)表示当字母个数为x时全部染为同一颜色的概率，\(E(x)\)表示当字母个数为x时全部染为同一颜色的期望步数，要染成的颜色是a，其余字母为b。
对于\(P(x)\)：显然有\(P(n)=1,P(0)=0\)。对于一个字符串有x个a的状态\(S_x\)，可以在下一步直接转移到状态\(S_{x-1},S_{x+1}\)。对于所有的选法，可以算出有\(i\times (n-i)\)种可以转移到\(S_{x-1}\)，有\(i\times(n-i)\)种转移到\(S_{x+1}\)，明显这两种转移概率相等。所以有\(P(x)=\frac{P(x-1)+P(x+1)}{2}\)，即\(P(x)-P(x-1)=P(x-1)-P(x-2)\)。所以数列\(P\)等差。易得\(P(x)=\frac x n\)。
然后我们计算\(E(x)\)：由上面所得结论，可以发现每次操作后x变化的选择有\(2\times x \times (n-x)\)，可以算出每次操作x变化的概率为\(\frac{2x(n-x)}{T}\)，所以操作使x变化的期望轮数为\(\frac{T}{2x(n-x)}\)。
值得注意的是，由于我们算期望\(E(x)\)表示有x个字母时完全染成同一颜色的期望步数，而\(P(x-1)\)与\(P(x+1)\)不等，所以\(E(x-1)\)与\(E(x+1)\)对\(E(x)\)带来的贡献的权重也不等，而带来的贡献的权重比就等于它们完全染成同一颜色的概率比。
因此我们得出：

\[\begin{aligned} E(x)&=\frac{P(x-1)\times E(x-1)+P(x+1)\times E(x+1)}{P(x-1)+P(x+1)}+\frac{T}{2x(n-x)}\\ &= \frac{(x-1)\times E(x-1)+(x+1)\times E(x+1)}{2x}+\frac{n(n-1)}{2x(n-x)} \end{aligned} \]

值得注意的是，我们求答案时求的是\(\sum\frac{E(cnt_i)\times i}{n}\)，不妨设\(f(x)=\frac{E(x)\times x}{n}\)。则上式可化为：

\[\begin{aligned} \frac{f(x)\times n}{x} &= \frac{f(x-1)\times n + f(x+1) \times n}{2x}+\frac{n(n-1)}{2x(n-x)} \\ 2f(x) &= f(x-1)+f(x+1)+\frac{n-1}{n-x} \\ f(x+1) &= 2f(x)-f(x-1)-\frac{n-1}{n-x}\end{aligned} \]

移项得到：
\(f(x+1)-f(x)=f(x)-f(x-1)-\frac{n-1}{n-x}\)。
容易得到\(E(n)=0\)，所以\(f(n)=0,f(0)=0\)。于是现在只要知道\(f(1)\)就能推出所有项。我们用\(g(x)\)表示\(f(x+1)-f(x)\)到\(f(x)-f(x-1)\)的修正量（即\((f(x)-f(x-1))-(f(x+1)-f(x))\)），用\(d(x)\)表示\(f(x+1)-f(x)\)。于是有：
\(d(x) = d(x-1)-g(x)\)，

\[\begin{aligned} f(x+1) &= f(x)+d(x) \\ &= f(x-1)+d(x-1)+d(x) \\ &= \cdots \\ &= f(0)+d(0)+d(1)+\cdots+d(x-1)+d(x) \\ &= f(0)+d(0)+(d(0)-g(0))+(d(0)-g(0)-g(1))+\cdots+(d(0)-\sum_{i=0}^{x}g(i)) \\ &= f(0)+x\cdot d(0)-(x-1)\cdot g(0)-(x-2)\cdot g(1)-\cdots-(x-(x-1))\cdot g(x) \end{aligned} \]

又因为\(f(0)=0，d(0)=f(1)\)，把\(g(x)\)代入：

\[\begin{aligned} f(x) &= x \cdot f(1)-(x-1)\cdot \frac{n-1}{n-1}-(x-2)\cdot \frac{n-1}{n-2}-\cdots-1 \cdot \frac{n-1}{n-(x-1)} \\ &= x \cdot f(1)+(n-1)\cdot(\frac{x-1}{n-1}+\frac{x-2}{n-2}+\cdots+\frac{x-(x-1)}{n-(x-1)}) \end{aligned} \]

现在让\(x=n\)，得到：
\(f(n)=n\cdot f(1)-(n-1)(n-1)=0\)
\(f(1)=\frac{(n-1)(n-1)}{n}\)。
然后递推即可得出答案。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e3 + 3;
int n;
int cnt[26];
string s;
double ans, f[N];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> s;
	n = s.length();
	for (rg int i = 0; i < n; i++) cnt[s[i] - 'A']++;
	f[0] = f[n] = 0;
	f[1] = 1.0 * (n - 1) * (n - 1) / n;
	for (rg int i = 2; i < n; i++) {
		f[i] = 2.0 * f[i - 1] - 1.0 * f[i - 2] - 1.0 * (n - 1) / (n - i + 1);
	}
	for (rg int i = 0; i < 26; i++) {
		ans += 1.0 * f[cnt[i]];
	}
	cout << fixed << setprecision(1) << ans << "\n";
	return qwq;
}

例题23：[JXOI2018] 游戏

首先观察\(l=1\)的情况，容易发现1的位置就是答案。再观察\(l=2\)的情况，又能发现最后一个质数的位置就是答案。总结一下可以发现，对于一个序列，总存在一些“质数”，他们之中最后一个的位置就是答案。
我们把这些“质数”称为关键数字，其定义为：在\([l,r]\)序列中，不是任何数的因子的数。于是在该序列中答案就是最后一个关键数字的位置。而总的答案则为最后一个关键数字的位置乘总情况数（即\(n!\)）。
要求最后一个关键数字的期望位置，不妨求排在所有关键数字后的非关键数字的期望个数。设有\(k\)个关键数字，任意一个非关键数字排在所有关键数字后面的概率\(P=\frac{1}{k+1}\)。由于有\(n-k\)个非关键数字，则排在所有关键数字后的非关键数字的期望个数\(E=(n-k)\times P=\frac{n-k}{k+1}\)。所以最后一个关键数字的期望位置\(E=n-\frac{n-k}{k+1}=\frac{k(n+1)}{k+1}\)。
则答案为\(\frac{k(n+1)}{k+1}\times n!=\frac{k}{k+1}(n+1)!\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
int l, r, n, k;
bool vis[10000003];
ll ans;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> l >> r;
	n = r - l + 1;
	for (rg int i = l; i <= r; i++) {
		if (!vis[i]) {
			k++;
			for (rg int j = 1; i * j <= r; j++) {
				vis[i * j] = true;
			}
		}
	}
	ans = k;
	for (rg int i = 2; i <= n + 1; i++) {
		if (i == k + 1) continue ;
		ans = 1ll * ans * i % mod;
	}
	cout << ans << "\n";
	return qwq;
}

例题24：[ABC263E] Sugoroku 3

令\(f[i]\)表示当前在第i格，到达n的期望步数。
\(\displaystyle f[i]=\frac{1}{A_i+1}\times \sum_{j=0}^{min(A_i,n-i)}(f[i+j]+1)\)
移项得：
\(\displaystyle f[i]=\frac{1}{A_i}\times \sum_{j=1}^{min(A_i,n-i}f[i+j]+\frac{min(A_i,n-i)+1}{A_i}\)
时间复杂度为\(O(\sum A_i)\)，会T，考虑使用后缀和优化。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 2e5 + 3, mod = 998244353;
inline ll qpow(ll a, ll b) {
	rg ll res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline ll inv(ll a) {
	return qpow(a, mod - 2) % mod;
}
int n;
ll a[N];
ll f[N], sum[N];  //后缀和 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i < n; i++) {
		cin >> a[i];
	}
	for (rg int i = n - 1; i >= 1; i--) {
		rg ll res = inv(a[i]), ret = sum[i + 1] - sum[min(a[i] + i, (ll)n) + 1];
		f[i] = (ret * res % mod + (min(a[i], (ll)n - i) + 1) * res % mod) % mod;
		sum[i] = (sum[i + 1] + f[i]) % mod;
	}
	cout << (f[1] % mod + mod) % mod << "\n";
	return qwq;
}

例题25：[ABC276F] Double Chance

可以发现，如果一个数比当前加入的数小，那么贡献即为加入的数，否则为更大的数。所以我们要维护比一个数小的个数与比一个数大的数的和。可以使用权值线段树，每个节点储存权值和与个数和两个东西。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 2e5 + 3, mod = 998244353;
int n, m, ans;
#define ls rt << 1
#define rs rt << 1 | 1
struct Tree {
	int val, num;
} t[N << 2];
inline void pushup(int rt) {
	t[rt].val = (t[ls].val + t[rs].val) % mod;
	t[rt].num = (t[ls].num + t[rs].num) % mod;
}
inline void update(int rt, int l, int r, int k) {
	if (l == r) {
		t[rt].val = (t[rt].val + k) % mod;
		t[rt].num = (t[rt].num + 1) % mod;
		return ;
	}
	rg int mid = (l + r) >> 1;
	if (mid >= k) update(ls, l, mid, k);
	else update(rs, mid + 1, r, k);
	pushup(rt);
}
inline int query_val(int rt, int l, int r, int ql, int qr) {  //数值和 
	if (ql <= l && r <= qr) {
		return t[rt].val;
	}
	rg int mid = (l + r) >> 1, res = 0;
	if (ql <= mid) res += query_val(ls, l, mid, ql, qr);
	if (qr > mid) res += query_val(rs, mid + 1, r, ql, qr);
	return res % mod;
}
inline int query_num(int rt, int l, int r, int ql, int qr) {  //个数和 
	if (ql <= l && r <= qr) {
		return t[rt].num;
	}
	rg int mid = (l + r) >> 1, res = 0;
	if (ql <= mid) res += query_num(ls, l, mid, ql, qr);
	if (qr > mid) res += query_num(rs, mid + 1, r, ql, qr);
	return res % mod;
}
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline int inv(int x) {
	return qpow(x, mod - 2) % mod;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		rg int a;
		cin >> a;
		ans = (ans + a * 2 * query_num(1, 1, N, 1, a)) % mod;
		ans = (ans + 2 * query_val(1, 1, N, a + 1, N)) % mod;
		ans = (ans + a) % mod;
		update(1, 1, N, a);
		cout << (ans * inv(i * i % mod) % mod + mod) % mod << "\n";
	}
	return qwq;
}

例题26：[ABC323E] Playlist

令\(f[i]\)表示第i秒之前恰好铺满的概率。则能使得选择1号歌后第x秒放1号歌的范围是\(\displaystyle\sum_{i=x-t[1]+1}^{x}\)，给它乘\(inv(n)\)即为答案。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e4 + 3, mod = 998244353;
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline int inv(int a) {
	return qpow(a, mod - 2) % mod;
}
int n, x;
int t[N];
int f[N];
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> x;
	rg int ret = inv(n);
	for (rg int i = 1; i <= n; i++) {
		cin >> t[i];
	}
	if (x < t[1]) {
		cout << ret << "\n";
		return qwq;
	}
	f[0] = 1;
	for (rg int i = 0; i < x; i++) {
		for (rg int j = 1; j <= n; j++) {
			if (i + t[j] > x) continue ;
			f[i + t[j]] = (f[i + t[j]] + f[i] * ret % mod) % mod;
		}
	}
	rg int ans = 0;
	for (rg int i = x - t[1] + 1; i <= x; i++) {
		ans = (ans + f[i]) % mod;
	}
	cout << ret * ans % mod << "\n";
	return qwq;
}

例题27：Assimilation IV

由于要求点数的期望，考虑将每个点的期望分开计算。
我们可以把每个点恰好在第i轮被选中的概率算出来，最后累加即为每个点被选中的概率。于是我们先预处理出每个点在第i轮能被几个城市覆盖到（记为\(cnt_i\)）。然后对于恰好在第i轮被选中即可表示为前\(i-1\)轮都未被选中的概率乘以第i轮被选中的概率，复杂度\(O(mn^2)\)，可以用前缀和处理cnt数组优化为\(O(mn)\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 5e4 + 3, mod = 998244353;
int n, m;
int d[23][N];
int cnt[23];
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline int inv(int x) { return qpow(x, mod - 2) % mod; }
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> m;
	for (rg int i = 1; i <= n; i++) {
		for (rg int j = 1; j <= m; j++) {
			cin >> d[i][j];
		}
	}
	rg int ans = 0;
	for (rg int i = 1; i <= m; i++) {
		for (rg int j = 1; j <= n; j++) cnt[j] = 0;
		for (rg int j = 1; j <= n; j++) {
			for (rg int k = 1; k <= n; k++) {  //第k轮 
				if (d[j][i] <= k) cnt[k]++;  //在第k轮能被几个城市覆盖到 
			}
		}
		rg int res = 0, sum = 1;
		for (rg int j = 1; j <= n; j++) {  //第j轮 
			rg int k = n - j + 1;  //最大的能被覆盖的值 
			res = (res + sum * cnt[k] % mod * inv(k) % mod) % mod;  //恰好在第i轮被选中的概率
			sum = sum * max(0ll, k - cnt[k]) % mod * inv(k) % mod;  //未被选中的概率 
		}
		ans = (ans + res) % mod;
	}
	cout << ans << "\n";
	return qwq;
}

例题28：Maxim and Restaurant

令状态\(f[i][j][k]\)表示前i个人选j个进去体积为k的方案数。
当一个人进不去时和前面进了哪些人以及进去的顺序是无关的，于是考虑枚举第一个不能进去的人，然后统计方案数。
具体地，枚举不能进去的人x，他进不去的条件是此时选中的j个人的体积满足\(p-k<a_x\)，在x之前进去的人可以任意排列，在x之后的人亦可以任意排列，所以乘上排列数与方案数，再乘上对答案的贡献（即进去的人数j），最后除以总的方案数\(n!\)得到答案：
\(\displaystyle\sum_{x=1}^{n}\sum_{j=1}^{n-1}\sum_{k=max(0,p-a_x+1)}^{p}j\times j!\times (n-j-1)!\times f[n][j][k]\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
#define db double
using namespace std;
const int N = 53;
int n, p;
db fac[N];
int a[N], f[N][N][N];
inline init() {
	fac[0] = 1;
	for (rg int i = 1; i <= n; i++) {
		fac[i] = 1.0 * i * fac[i - 1];
	}
}
db ans;
int sum;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> a[i];
		sum += a[i];
	}
	cin >> p;
	if (sum <= p) {
		cout << fixed << setprecision(10) << 1.0 * n << "\n";
		return qwq;
	}
	init();
	for (rg int x = 1; x <= n; x++) {  //第一个不能进去的人 
		memset(f, 0, sizeof(f));
		f[0][0][0] = 1;
		for (rg int i = 1; i <= n; i++) {
			for (rg int j = 0; j <= i; j++) {
				for (rg int k = 0; k <= p; k++) {
					f[i][j][k] = f[i - 1][j][k];
					if (i == x) {  //x无法进入，直接跳过
						continue ;
					}
					if (k >= a[i] && j > 0) {
						f[i][j][k] += f[i - 1][j - 1][k - a[i]];
					}
				}
			}
		}
		for (rg int j = 1; j < n; j++) {
			for (rg int k = max(0ll, p - a[x] + 1); k <= p; k++) {
				ans += j * fac[j] * fac[n - j - 1] * f[n][j][k];
			}
		}
	}
	cout << fixed << setprecision(10) << ans / fac[n] << "\n";
	return qwq;
}

例题29：Fafa and Ancient Alphabet

分类讨论：

• 1.\(a_i=0\)并且\(x=0\)，则\(a_i>x\)的概率为\(\frac{(m-1)\times(m-2)\times\cdots\times 0}{m^2}=\frac{\frac{1}{2}(m-1)m}{m^2}=\frac{m-1}{2m}\)，\(a_i=x\)的概率为\(\frac{1}{m}\)。
• 2.\(a_i=0\)，则\(a_i>x\)的概率为\(\frac{m-x}{m}\)，\(a_i=x\)的概率为\(\frac 1 m\)。
• 3.\(x=0\)，则\(a_i>x\)的概率为\(\frac{a_i-1}{m}\)，\(a_i=x\)的概率为\(\frac 1 m\)。
• 4.\(a_i\ne 0\)并且\(x\ne0\)，若\(a_i=x\)继续向后；若\(a_i<x\)，直接退出；若\(a_i>x\)，给答案加上\(\frac{1}{m}^{cnt}\)，其中cnt表示前面有多少位存在0（因为若能到达这一位，则前面的\(a_i\)与\(x\)都相等）。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e5 + 3, mod = 1e9 + 7;
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline int inv(int x) { return qpow(x, mod - 2) % mod; }
int n, m;
int a[N];
int ans, cnt = 1;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> m;
	rg int res = inv(m);
	for (rg int i = 1; i <= n; i++) cin >> a[i];
	for (rg int i = 1; i <= n; i++) {
		rg int x;
		cin >> x;
		if (a[i] == 0 && x == 0) {
			ans = (ans + cnt * (m - 1) % mod * inv(2 * m) % mod) % mod;
			cnt = cnt * res % mod;
		} else if (a[i] == 0) {
			ans = (ans + cnt * (m - x) % mod * res % mod) % mod;
			cnt = cnt * res % mod;
		} else if (x == 0) {
			ans = (ans + cnt * (a[i] - 1) % mod * res % mod) % mod;
			cnt = cnt * res % mod;
		} else {
			if (a[i] > x) {
				ans = (ans + cnt) % mod;
				break ;
			} else if (a[i] < x) {
				break ;
			}
		}
	}
	cout << ans << "\n";
	return qwq;
}

例题30：Score of a Tree

先来观察样例中根节点对\(F(A)\)的贡献。很显然，第0秒时根节点贡献为1，第1秒时根节点贡献为\(1\wedge0=1\)，第2秒时根节点贡献为\(0\wedge1\wedge1=0\)。
可以发现，第0秒时根节点的权值为它本身，第1秒为它所有儿子节点的异或和，第2秒为它所有孙子节点的异或和……直到时间t超过这个树的深度。
可以发现，所有节点都遵循这个规律。
接下来考虑\(2^n\)种情况。对于某个节点，有一半的概率它0秒的权值为1，有一半的概率它第1秒的权值即它的儿子节点的异或和为1，有一半的概率它第2秒的权值即它的孙子节点的异或和为1……而这一半的概率对应的是\(2^{n-1}\)种情况。
我们令第i个节点为第\(s_i\)层且\(s_i=max\{s_{v_i}\}+1\)，其中\(v_i\)表示i的儿子节点。特殊的，\(s_1=1\)。
可以得到，第i个节点自身共有\(2^n\)种情况，其中有\(2^{n-1}\)种是1，即有\(2^{n-1}\)的贡献。又因为每次转移i也有\(2^{n-1}\)的贡献，且有\(s_i-1\)次转移，所以总的贡献为\(s_i\times 2^{n-1}\)。
于是答案为\(\displaystyle2^{n-1}\times\sum_{i=1}^{n} s_i\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 2e5 + 3, mod = 1e9 + 7;
int T, n;
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
vector<int> e[N];
int s[N];
int ans;
inline void dfs(int u, int fath) {
	if (e[u].size() == 1 && u != 1) {
		s[u] = 1;
		return ;
	}
	rg int res = 0;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (v == fath) continue ;
		dfs(v, u);
		res = max(res, s[v]);
	}
	s[u] = res + 1;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> T;
	while (T--) {
		ans = 0;
		cin >> n;
		for (rg int i = 1; i < n; i++) {
			rg int u, v;
			cin >> u >> v;
			e[u].push_back(v);
			e[v].push_back(u);
		}
		dfs(1, 0);
		for (rg int i = 1; i <= n; i++) {
			ans = (ans + s[i]) % mod;
		}
		cout << qpow(2, n - 1) * ans % mod << "\n";
		for (rg int i = 1; i <= n; i++) {
			s[i] = 0;
			e[i].clear();
		}
	}
	return qwq;
}

例题31：[ABC297F] Minimum Bounding Box 2

容斥好题。
考虑所有贡献 \(\displaystyle\sum^{A}s=\sum_{i=1}^{n}\sum_{j=1}^{m}ss_{i,j}\)，而我们要求的就是每一个点在多少个矩形中出现（即贡献了多少次）。
这里，A是所有子矩形，s是每个矩形的大小，也即每个子矩形的贡献。
我们考虑这样一个点：

我们希望求出所有包含它的子矩形的数量（在剩下\(k-1\)个点随机时）。然而这很难求，我们考虑容斥，即求不包含这一个点的矩形的数量。显然，我们要让所有k个点都在这个点上面/下面/左面/右面。例如在上面的情况：

假设这个点为\((i,j)\)，那么这时子矩形的数量为\(C((i-1)\cdot m,k)\)。在上面、下面、右面同理。
还有一个问题：我们可能算重。比如我们计算了左面和上面的贡献，左上角的矩形就会被算重：

这时我们显然要减去\(C((i-1)\times(j-1),k)\)。依此计算即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e6 + 3, mod = 998244353;
int H, W, K;
inline int qpow(int a, int b) {
	rg int res = 1;
	while (b) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
inline int inv(int x) { return qpow(x, mod - 2) % mod; }
int f[N];
inline void init() {
	f[0] = 1;
	for (rg int i = 1; i <= H * W; i++) {
		f[i] = f[i - 1] * i % mod;
	}
}
inline int C(int n, int m) {
	if (n < m) return qwq;
	return f[n] * qpow(f[m], mod - 2) % mod * qpow(f[n - m], mod - 2) % mod;
}
int ans, res;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> H >> W >> K;
	if (K == 1) {
		cout << 1 << "\n";
		return qwq;
	}
	init();
	ans = C(H * W, K);
	res = ans;
	for (rg int i = 1; i <= H; i++) {
		for (rg int j = 1; j <= W; j++) {
			rg int u, d, l, r, ul, ur, dl, dr;
			u = C((i - 1) * W, K);
			d = C((H - i) * W, K);
			l = C((j - 1) * H, K);
			r = C((W - j) * H, K);
			ul = C((i - 1) * (j - 1), K);
			ur = C((i - 1) * (W - j), K);
			dl = C((H - i) * (j - 1), K);
			dr = C((H - i) * (W - j), K);
			res = (res + ans - u - d - l - r + ul + ur + dl + dr) % mod;
			res = (res + mod) % mod;
		}
	}
	//cout << res << "\n";
	cout << res * inv(ans) % mod - 1 << "\n";
	return qwq;
}

完结撒花~

标签：概率,frac,int,times,rg,期望,dp
From： https://www.cnblogs.com/Baiyj/p/18242893