[NOIP2012 提高组] 开车旅行
题目描述
小 \(\text{A}\) 和小 \(\text{B}\) 决定利用假期外出旅行,他们将想去的城市从 $1 $ 到 \(n\) 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 \(i\) 的海拔高度为\(h_i\),城市 \(i\) 和城市 \(j\) 之间的距离 \(d_{i,j}\) 恰好是这两个城市海拔高度之差的绝对值,即 \(d_{i,j}=|h_i-h_j|\)。
旅行过程中,小 \(\text{A}\) 和小 \(\text{B}\) 轮流开车,第一天小 \(\text{A}\) 开车,之后每天轮换一次。他们计划选择一个城市 \(s\) 作为起点,一直向东行驶,并且最多行驶 \(x\) 公里就结束旅行。
小 \(\text{A}\) 和小 \(\text{B}\) 的驾驶风格不同,小 \(\text{B}\) 总是沿着前进方向选择一个最近的城市作为目的地,而小 \(\text{A}\) 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 \(x\) 公里,他们就会结束旅行。
在启程之前,小 \(\text{A}\) 想知道两个问题:
1、 对于一个给定的 \(x=x_0\),从哪一个城市出发,小 \(\text{A}\) 开车行驶的路程总数与小 \(\text{B}\) 行驶的路程总数的比值最小(如果小 \(\text{B}\) 的行驶路程为 \(0\),此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 \(\text{A}\) 开车行驶的路程总数与小 \(\text{B}\) 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2、对任意给定的 \(x=x_i\) 和出发城市 \(s_i\),小 \(\text{A}\) 开车行驶的路程总数以及小 \(\text B\) 行驶的路程总数。
输入格式
第一行包含一个整数 \(n\),表示城市的数目。
第二行有 \(n\) 个整数,每两个整数之间用一个空格隔开,依次表示城市 \(1\) 到城市 \(n\) 的海拔高度,即 \(h_1,h_2 ... h_n\),且每个 \(h_i\) 都是互不相同的。
第三行包含一个整数 \(x_0\)。
第四行为一个整数 \(m\),表示给定 \(m\) 组 \(s_i\) 和 \(x_i\)。
接下来的 \(m\) 行,每行包含 \(2\) 个整数 \(s_i\) 和 \(x_i\),表示从城市\(s_i\) 出发,最多行驶 \(x_i\) 公里。
输出格式
输出共 \(m+1\) 行。
第一行包含一个整数 \(s_0\),表示对于给定的 \(x_0\),从编号为 \(s_0\) 的城市出发,小 \(\text A\) 开车行驶的路程总数与小 \(\text B\) 行驶的路程总数的比值最小。
接下来的 \(m\) 行,每行包含 \(2\) 个整数,之间用一个空格隔开,依次表示在给定的 \(s_i\) 和 \(x_i\) 下小 \(\text A\) 行驶的里程总数和小 \(\text B\) 行驶的里程总数。
样例 #1
样例输入 #1
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3
样例输出 #1
1
1 1
2 0
0 0
0 0
样例 #2
样例输入 #2
10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7
样例输出 #2
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0
提示
【样例1说明】
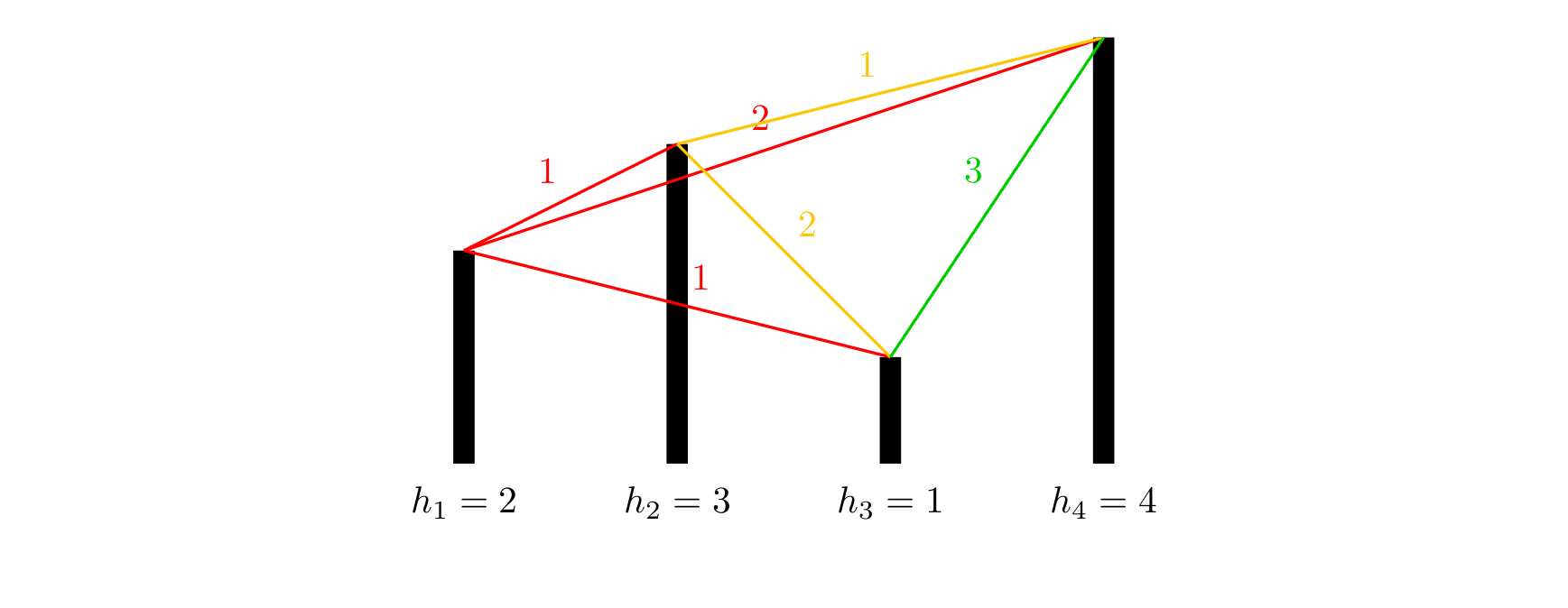
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 \(1\) 出发,可以到达的城市为 \(2,3,4\),这几个城市与城市 \(1\) 的距离分别为 \(1,1,2\),但是由于城市 \(3\) 的海拔高度低于城市 \(2\),所以我们认为城市 \(3\) 离城市 \(1\) 最近,城市 \(2\) 离城市 \(1\) 第二近,所以小A会走到城市 \(2\)。到达城市 \(2\) 后,前面可以到达的城市为 \(3,4\),这两个城市与城市 \(2\) 的距离分别为 \(2,1\),所以城市 \(4\) 离城市 \(2\) 最近,因此小B会走到城市\(4\)。到达城市 \(4\) 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 \(2\) 出发,可以到达的城市为 \(3,4\),这两个城市与城市 \(2\) 的距离分别为 \(2,1\),由于城市 \(3\) 离城市 \(2\) 第二近,所以小 \(\text A\) 会走到城市 \(3\)。到达城市 \(3\) 后,前面尚未旅行的城市为 \(4\),所以城市 \(4\) 离城市 \(3\) 最近,但是如果要到达城市 \(4\),则总路程为 \(2+3=5>3\),所以小 \(\text B\) 会直接在城市 \(3\) 结束旅行。
如果从城市 \(3\) 出发,可以到达的城市为 \(4\),由于没有离城市 \(3\) 第二近的城市,因此旅行还未开始就结束了。
如果从城市 \(4\) 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【样例2说明】
当 \(x=7\) 时,如果从城市 \(1\) 出发,则路线为 \(1 \to 2 \to 3 \to 8 \to 9\),小 \(\text A\) 走的距离为 \(1+2=3\),小 \(\text B\) 走的距离为 \(1+1=2\)。(在城市 \(1\) 时,距离小 \(\text A\) 最近的城市是 \(2\) 和 \(6\),但是城市 \(2\) 的海拔更高,视为与城市 \(1\) 第二近的城市,所以小 \(\text A\) 最终选择城市 \(2\);走到\(9\) 后,小 \(\text A\) 只有城市 \(10\) 可以走,没有第二选择可以选,所以没法做出选择,结束旅行)
如果从城市 \(2\) 出发,则路线为 \(2 \to 6 \to 7\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为 \(2,4\)。
如果从城市 \(3\) 出发,则路线为 \(3 \to 8 \to 9\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为\(2,1\)。
如果从城市 \(4\) 出发,则路线为 \(4 \to 6 \to 7\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为 \(2,4\)。
如果从城市 \(5\) 出发,则路线为 \(5 \to 7 \to 8\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为 \(5,1\)。
如果从城市 \(6\) 出发,则路线为 \(6 \to 8 \to 9\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为\(5,1\)。
如果从城市 \(7\) 出发,则路线为 \(7 \to 9 \to 10\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为\(2,1\)。
如果从城市 \(8\) 出发,则路线为 \(8 \to 10\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为\(2,0\)。
如果从城市 \(9\) 出发,则路线为 \(9\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为 \(0,0\)(旅行一开始就结束了)。
如果从城市 \(10\) 出发,则路线为 \(10\),小 \(\text A\) 和小 \(\text B\) 走的距离分别为\(0,0\)。
从城市 \(2\) 或者城市 \(4\) 出发小 \(\text A\) 行驶的路程总数与小 \(\text B\) 行驶的路程总数的比值都最小,但是城市 \(2\) 的海拔更高,所以输出第一行为 \(2\)。
【数据范围与约定】
对于 \(30\%\) 的数据,有\(1\le n \le 20,1\le m\le 20\);
对于\(40\%\) 的数据,有\(1\le n \le 100,1\le m\le 100\);
对于 \(50\%\) 的数据,有\(1\le n \le 100,1\le m\le 1000\);
对于 \(70\%\) 的数据,有\(1\le n \le 1000,1\le m\le 10^4\);
对于 \(100\%\) 的数据:\(1\le n,m \le 10^5\),\(-10^9 \le h_i≤10^9\),\(1 \le s_i \le n\),\(0 \le x_i \le 10^9\)
数据保证 \(h_i\) 互不相同。
题解
本题有三个关键信息:已行驶的天数,所在城市,小A和小B各自行驶的路程长度;
若已知出发城市与天数,即可求得小A和小B各自行驶的路程长度,并且依据题意,天数还能反映谁现在在开车,所以我们可以把“天数” 作为“阶段”进行状态设计;
定义 $ f[i][j][k] $ 表示从城市 $ j $ 出发,两人共行驶 $ i $ 天,$ k $ 先开车,最终会到达的城市;
很显然,这样开会炸内存,而天数又可以随意划分,可以考虑倍增优化;
重定义 $ f[i][j][k] $ 表示从城市 $ j $ 出发,两人共行驶 $ 2^i $ 天,$ k $ 先开车,最终会到达的城市;
其中 $ 0 $ 代表小A先开车, $ 1 $ 代表小B先开车;
对于初始化,我们现在知道谁先开车,要求到那个城市,只需知道小A或小B在某一个城市时,下一个会到哪里即可,可以预处理出两个数组 $ ga[i] $ 和 $ gb[i] $ 分别表示小A在城市 $ i $ 时,下一个会到哪个城市和小B在城市 $ i $ 时,下一个会到哪个城市;
对于问题 $ 2 $,我们可以同时维护两个数组 $ da[i][j][k] $ 和 $ db[i][j][k] $ 分别表示从城市 $ j $ 出发,两人共行驶 $ 2^i $ 天,$ k $ 先开车,小A行驶的路程总长度以及小B行驶的路程总长度;
对于问题 $ 1 $,我们只需枚举出发点,找最小的即可;
则:
- 对于预处理
因为小A和小B只能往后走,所以我们可以从后往前遍历,并同时维护一个单调递增的序列(可以用 $ multiset $)其实应该是平衡树,但我不会,每次只需找当前节点旁边一位或两位的最小值和次小值即可(建议参考下面的代码);
- 对于初始化
- 对于状态转移方程
- 对于 $ da $ 和 $ db $ 的初始化
对于 $ dis $ 的维护,可以在维护单调递增的序列同时顺便维护;
- 对于$ da $ 和 $ db $的状态转移方程
这里 $ i = 1 $ 时不同,因为 \(2^1\) 只能拆成两个$ 2^0 $ ,$ 2^0 = 1 $ 是奇数,开车的人不同,其它的是偶数,开车的人相同;
#include <iostream>
#include <set>
#include <cmath>
using namespace std;
int n;
int h[10000005];
int x0, m;
struct sss{
long long id, he;
bool operator <(const sss &A) const {
return he < A.he;
}
};
long long f[18][100005][2]; // 0 a, 1 b;
long long da[18][100005][2];
long long db[18][100005][2];
multiset<sss> p;
void init() {
p.insert({0, 9999999999999999});
p.insert({0, 9999999999999999});
p.insert({n + 1, -9999999999999999});
p.insert({n + 1, -9999999999999999}); //防止访问越界
for (long long i = n; i >= 1; i--) {
long long ga, gb;
p.insert({i, h[i]});
multiset<sss>::iterator q = p.lower_bound({i, h[i]});
q--;
long long lid = (*q).id, lh = (*q).he;
q++;
q++;
long long rid = (*q).id, rh = (*q).he;
q--;
if (abs(rh - h[i]) >= abs(lh - h[i])) {
gb = lid;
q--; q--;
if (abs(rh - h[i]) < abs((*q).he - h[i])) {
ga = rid;
} else {
ga = (*q).id;
}
} else {
gb = rid;
q++; q++;
if (abs((*q).he - h[i]) < abs(lh - h[i])) {
ga = (*q).id;
} else {
ga = lid;
}
}
f[0][i][0] = ga;
f[0][i][1] = gb;
da[0][i][0] = abs(h[ga] - h[i]);
db[0][i][1] = abs(h[gb] - h[i]);
}
}
pair<long long, long long> w(long long s, long long x) {
long long p = s;
long long la = 0;
long long lb = 0;
for (int i = 17; i >= 0; i--) {
if (f[i][p][0] && la + lb + da[i][p][0] + db[i][p][0] <= x) {
la += da[i][p][0];
lb += db[i][p][0];
p = f[i][p][0];
}
}
return {la, lb};
}
int main() {
cin >> n;
for (long long i = 1; i <= n; i++) cin >> h[i];
cin >> x0;
cin >> m;
init();
long long tt = 10;
for (int i = 1; i <= 17; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 0; k <= 1; k++) {
if (i == 1) {
f[i][j][k] = f[0][f[0][j][k]][1 - k];
da[i][j][k] = da[0][f[0][j][k]][1 - k] + da[0][j][k];
db[i][j][k] = db[0][f[0][j][k]][1 - k] + db[0][j][k];
} else {
f[i][j][k] = f[i - 1][f[i - 1][j][k]][k];
da[i][j][k] = da[i - 1][j][k] + da[i - 1][f[i - 1][j][k]][k];
db[i][j][k] = db[i - 1][j][k] + db[i - 1][f[i - 1][j][k]][k];
}
}
}
}
long double ans = 1.00 * 0x3f3f3f3f;
long long an = 0;
for (int i = 1; i <= n; i++) {
pair<long long, long long> a = w(i, x0);
long long la = a.first;
long long lb = a.second;
if (lb == 0) continue;
long double d = 1.00 * la / (1.00 * lb);
if (d < ans) {
ans = d;
an = i;
} else if (d == ans) {
if (h[an] < h[i]) an = i;
}
}
cout << an << endl;
long long a, b;
for (int i = 1; i <= m; i++) {
cin >> a >> b;
pair<long long, long long> c = w(a, b);
cout << c.first << ' ' << c.second << endl;
}
return 0;
}