前言
习题博客:link。
因为各种原因,这个博客是赶出来的,所以大概率会有没讲清楚或者讲错了的情况,请大家及时指出。
因为个人不是非常擅长于 DP,可能很难判别一道题的好坏,所以可能存在几道史题在题单中,请大家谅解。
这篇博客理论上仅限于讲解例题,大部分习题的题解请移步至配套博客查看。关于习题:就是我认为大家做完上一道题之后能自己做出来的题。
那么就让我们开始吧。
DP 是什么
DP(Dynamic Programming),动态规划,通常用于处理最优性问题,也可以用来计数等。其核心思想就是设置状态,使得这些状态能够进行转移,最后得出结果。
另一种理解方式就是,DP 能够通过设置状态转移的方式来缩小问题规模,就比如我们推出了一个从前 \(i\) 个物品转移到前 \(i+1\) 个物品的转移式,我们就成功把问题规模从 \(n\) 变成了 \(1\),因为这里存在一个从 \(1\) 到 \(n\) 的递推关系。
DP 优于暴力就是因为,暴力的时候,我们其实会重复处理很多信息,而 DP 通过设置状态并储存状态信息来进行一个类似于记忆化的过程,从而省去了很多很多重复的计算。
举一个非常简单的例子:
最长公共子序列问题:
给定两个串 \(S,T\),可以删除 \(S\) 中的一些元素,将 \(S\) 中剩下元素按原顺序拼在一起组成串 \(A\);对 \(T\) 进行一样的操作得到 \(B\),求最长的 \(A\) 的长度 \(l\) 使得 \(\exist A,B,|A|=|B|=l, A=B\)。
我们可以设置状态 \(f_{i,j}\) 代表这个最长的子序列放到 \(S\) 的原位置中最后位置的下标 \(\leq i\),放到 \(T\) 的原位置中最后位置的下标 \(\leq j\) 时的最长子序列长度。我们发现有转移:
\[f_{i+1,j+1}=\max(f_{i,j}+[S_{i+1}=T_{j+1}],f_{i+1,j},f_{i,j+1}) \]这样我们可以在 \(O(|S||T|)\) 的时间复杂度内解决这个问题。这比暴力的 \(O(2^{|S|}+2^{|T|})\) 好多了。
DP 的前置条件
能用 DP 解决的问题通常需要满足三个条件,即最优子结构,无后效性,子问题重叠。
- 最优子结构
这个指子问题的最优解能够转移到原问题的最优解。满足这个条件的问题有些时候也可以用贪心做。
- 无后效性
前面子问题的解不会受后面决策的影响。
- 子问题重叠
如果没有重叠的子问题,那么 DP 其实和暴力是等复杂度的。
对于大多数题,如果计算的贡献完整且没有重复,然后无后效性,这个 DP 大概率就是正确的。
朴素 DP
就是什么特殊类 DP 都不是的纯暴力 DP,放到开头给大家练练手。
*1800,想必大家都能独立切掉。
给你一个长为 \(n\) 的字符串 \(s\) 以及 \(a_{1..n}\),删去第 \(i\) 个字符的代价为 \(a_i\),你需要删去一些字符(如果一开始就符合条件当然可以不删)使得剩下的串中不含子序列 "hard",求最小代价。
子序列不需要连续。
\(n\leq 10^5,a_i\in[1,998244353]\)。
题解
我们设状态 \(f_{i,j}\) 表示前 \(i\) 个字符中,hard 仅前 \(j\) 个字符已经匹配完成的最小代价。
转移是简单的。如果当前位是 h,那么有:
第一个式子代表不删这个 h 时的转移,第二个式子则代表删掉这个 h 之后的转移。
当前位为其他值类似,最后的答案就是 \(\min_if_{n,i}\)。时间复杂度为 \(O(n)\)。空间可以滚动。
代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[100005];
long long f[100005][4];
int a[100005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
memset(f,0x3f,sizeof f);
f[0][0]=0;
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
for(int j=0;j<=3;j++)f[i][j]=f[i-1][j];
if(s[i]=='h')f[i][1]=min(f[i][1],f[i-1][0]),f[i][0]=f[i-1][0]+a[i];
else if(s[i]=='a')f[i][2]=min(f[i][2],f[i-1][1]),f[i][1]=f[i-1][1]+a[i];
else if(s[i]=='r')f[i][3]=min(f[i][3],f[i-1][2]),f[i][2]=f[i-1][2]+a[i];
else if(s[i]=='d')f[i][3]=f[i-1][3]+a[i];
}
cout<<min({f[n][0],f[n][1],f[n][2],f[n][3]});
return 0;
}
例题:P1410 子序列
要想学好 DP,首先要练习如何吃史。
给定一个长度为 \(N\)(\(N\) 为偶数)的序列,问能否将其划分为两个长度为 \(N / 2\) 的严格递增子序列。
\(N\leq 2000\)。
题解
这题的状态设计非常神秘。
设 \(f_{i,j}\) 为前 \(i\) 个元素可以拆成两个递增子序列,第一个的长度为 \(j\),并且最后一位对应的下标是 \(i\),第二个的最大值的最小值。
因为存的是最小值,我们就能较为方便的转移。
假设下一个元素 \(i+1\) 的值 \(a_{i+1}>f_{i,j}\),那么这里可以直接扩展第二个子序列,有 \(f_{i+1,i-j+1}\gets a_i\)。
如果 \(a_{i+1}>a_i\),这里也可以直接扩展第一个子序列,有 \(f_{i+1,j+1}\gets f_{i,j}\)。
其他情况均不能扩展任何子序列。
最后判定 \(f_{n,\frac{n}{2}}\) 是不是 \(+\infty\) 就行了。
最初做这道题的时候,作者认为这道题非常史。
代码
#include<bits/stdc++.h>
using namespace std;
int f[2005][2005];
int a[2005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int n;
while(cin>>n){
for(int i=1;i<=n;i++)cin>>a[i];
memset(f,0x3f,sizeof f);
f[1][1]=0;
for(int i=1;i<n;i++){
for(int j=1;j<=i;j++){
if(a[i+1]>f[i][j])f[i+1][i-j+1]=min(f[i+1][i-j+1],a[i]);
if(a[i+1]>a[i])f[i+1][j+1]=min(f[i+1][j+1],f[i][j]);
}
}
if(f[n][n/2]<=1000000000)cout<<"Yes!\n";
else cout<<"No!\n";
}
return 0;
}
顺带一提,这题有双倍经验 P4728。
选做题:P4740 [CERC2017] Embedding Enumeration
作者认为,分讨是 DP 的一大重点。
输入一棵有标号树,求把这棵树放入 \(2*n\) 的网格图中的方案数,对 \(10^9+7\) 取模。
两种方案相同当且仅当网格图内标号分布完全相同。
要求:\(1\) 必须放在 \((1,1)\),有边连接的节点必须相邻,两个节点不能放在同一个格子。
\(n\leq 3\times 10^5\)。
Hint
大家可以尝试直接对某个节点在左上角时的方案数进行分类讨论。
题解
作者的分类讨论和代码都非常复杂,仅供参考!!!
另外,因为这个题调不出来会很难受,所以作者提供数据,内网,外网。
设 \(f_i\) 为树上的点 \(i\) 在左上角时放 \(i\) 的子树的方案数。
有 \(4\) 种大情况:
第一种:
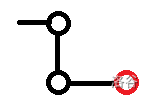
注意到这里的左上角黑点不一定就是 \(i\),也有可能是 \(i\) 的子孙。注意这个子孙到 \(i\) 中间经过的所有点度数为 \(2\),否则会和下面的情况重复一些。
这个时候的贡献就是红色的点的 DP 值,我们需要记录树上的这种链(链顶到链底的父亲都只有一个儿子)的 DP 值和。
第二种:
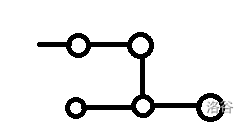
需要判断左下链的合法性,贡献为右下的点的 DP 值。
第三种:
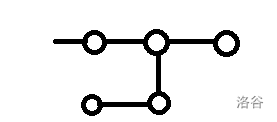
下面的子树可以往左摆或者往右摆。
向左摆是简单的,但是向右摆的话就要满足这两棵子树中至少有一个是链,贡献就是某个子树第一次超过另外一个链的点的 DP 值,没有超过也有 \(1\) 的贡献。
这里可能需要记录 DFS 序来实现 \(O(1)\) 转移。
注意如果下面的子树大小就只有 \(1\),注意向左摆和向右摆只能算一个,不然会算重。
第四种:
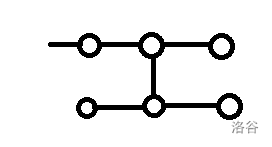
这里有三个子树,我们把左下子树称为 \(a\) 子树,右下子树称为 \(b\) 子树,右上子树称为 \(c\) 子树。
显然 \(a\) 子树一定是链,我们只用保证 \(b,c\) 子树其中有至少一个是链就行了,贡献和第三种是一致的。
注意如果 \(i\) 的子树就是链,还要特判一条直链,一条直链最后拐下来一格,还有拐下来后只往左摆。
可能还要特判 \(i\) 有两个儿子的情况。
作者的实现非常史,代码中分了 \(7\) 种情况,其中 Situation 1 对应这里的第一种情况;Situation 2 对应这里的第二种情况;Situation 3-5 对应这里的第三种情况;Situation 6 对应这里的第四种情况;Situation 7 说的是一条链拐下来之后向左摆(摆的长度 \(>1\))的情况。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
#define int long long
vector<int> son[300005];
int f[300005],fa[300005],sum[300005],len[300005],edid[300005];
int tst[300005],dfn[300005],rk[300005],dfncnt;
vector<int> to[300005];
void init(int now,int f){
fa[now]=f;
dfn[now]=++dfncnt;
rk[dfncnt]=now;
for(auto v:to[now]){
if(v^f){
son[now].push_back(v);
init(v,now);
}
}
if(son[now].size()==1){
len[now]=len[son[now][0]]+1;
edid[now]=edid[son[now][0]];
if(!edid[now])edid[now]=son[now][0];
tst[now]=tst[son[now][0]];
}else if(son[now].size()==2)tst[now]=1,edid[now]=now;
else if(son[now].size()>2){
cout<<0;
exit(0);
}
return;
}
int n,x,y;
void dfs(int now){
for(auto v:son[now])dfs(v);
int &p=f[now];
//Situation 1
if(len[now]>=2)p=(p+sum[son[son[now][0]][0]]);
//Situation 7
if(!tst[now]&&len[now]>=3)p=(p+len[now]-2-(len[now]/2)+1)%mod;
//SP-Straight segment
if(!tst[now])p=(p+1)%mod;
//SP-len>=1
// ------
// |
if(!tst[now]&&len[now]>=1)p=(p+1)%mod;
//Situation 2-6
if(tst[now]){
//get next deg-3 point
int nxt3=edid[now];
//SP-now is deg-3 point
if(nxt3==now){
//sub1:2 segments
if(!tst[son[now][0]]&&!tst[son[now][1]]){
int mx=len[son[now][0]]>len[son[now][1]]?son[now][0]:son[now][1];
int mi=mx==son[now][0]?son[now][1]:son[now][0];
p=(p+f[rk[dfn[mx]+len[mi]]])%mod;
if(len[mx]>len[mi]+1)p=(p+f[rk[dfn[mx]+len[mi]+2]]%mod)%mod;
else p=(p+1)%mod;
}//sub2:1 tree,1 segment
else if(tst[son[now][0]]+tst[son[now][1]]==1){
int _1=tst[son[now][0]]==1?son[now][0]:son[now][1];
int _0=tst[son[now][0]]==0?son[now][0]:son[now][1];
if(len[_1]>=len[_0])p=(p+f[rk[dfn[_1]+len[_0]]])%mod;
if(len[_1]>=len[_0]+2)p=(p+f[rk[dfn[_1]+len[_0]+2]])%mod;
}
}else{
//Situation 2
if(dfn[nxt3]-dfn[now]>=2){
int nxtlen=dfn[nxt3]-dfn[now]-1;
if(!tst[son[nxt3][0]]&&len[son[nxt3][0]]<nxtlen)p=(p+f[son[nxt3][1]])%mod;
if(!tst[son[nxt3][1]]&&len[son[nxt3][1]]<nxtlen)p=(p+f[son[nxt3][0]])%mod;
}
//Situation 3
if(!tst[son[nxt3][0]]&&!tst[son[nxt3][1]]){
//Copy upper code-deal RR situation
int mx=len[son[nxt3][0]]>len[son[nxt3][1]]?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
p=(p+f[rk[dfn[mx]+len[mi]]])%mod;
if(len[mx]>len[mi]+1)p=(p+f[rk[dfn[mx]+len[mi]+2]])%mod;
else p=(p+1)%mod;
//deal LR situation
if(len[now]>=len[mi]&&len[mi]!=0)p=(p+f[mx])%mod;
if(len[now]>=len[mx]&&len[mx]!=0)p=(p+f[mi])%mod;
}
//Situation 4-5
if(tst[son[nxt3][0]]+tst[son[nxt3][1]]==1){
int mx=tst[son[nxt3][0]]?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
//Situation 4
if(len[mi]<=len[now]&&len[mi]!=0)p=(p+f[mx])%mod;
if(len[mx]>=len[mi])p=(p+f[rk[dfn[mx]+len[mi]]]%mod)%mod;
//Situation 5
if(len[mx]>=len[mi]+2)p=(p+f[rk[dfn[mx]+len[mi]+2]]%mod)%mod;
}
//Situation 6
// -------
// |
// -------
//shape
//this is a large situation!!!
if(max(son[son[nxt3][0]].size(),son[son[nxt3][1]].size())==2&&son[son[nxt3][0]].size()+son[son[nxt3][1]].size()<=3){
int mx=son[son[nxt3][0]].size()==2?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
int _1=mi,_2=son[mx][0],_3=son[mx][1];
//sub1: 3 segments
if(tst[_1]+tst[_2]+tst[_3]==0){
if(len[now]>len[_2]){
int __1=len[_1]>len[_3]?_1:_3;
int __2=len[_1]<len[_3]?_1:_3;
if(len[__1]==len[__2])p=(p+1)%mod;
else p=(p+f[rk[dfn[__1]+len[__2]+1]])%mod;
}
if(len[now]>len[_3]){
int __1=len[_1]>len[_2]?_1:_2;
int __2=len[_1]<len[_2]?_1:_2;
if(len[__1]==len[__2])p=(p+1)%mod;
else p=(p+f[rk[dfn[__1]+len[__2]+1]])%mod;
}
}
//sub2: 2 segments 1 tree
if(tst[_1]+tst[_2]+tst[_3]==1){
if(tst[_1]==1){
if(len[_2]<len[now]&&len[_3]<len[_1])p=(p+f[rk[dfn[_1]+len[_3]+1]])%mod;
if(len[_3]<len[now]&&len[_2]<len[_1])p=(p+f[rk[dfn[_1]+len[_2]+1]])%mod;
}else{
if(tst[_2]!=1)swap(_2,_3);
if(len[_3]<len[now]&&len[_1]<len[_2])p=(p+f[rk[dfn[_2]+len[_1]+1]])%mod;
}
}
}
}
}
sum[now]=f[now];
if(son[now].size()==1)sum[now]=(sum[now]+sum[son[now][0]])%mod;
return;
}
signed main(){
f[0]=1;
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<n;i++)cin>>x>>y,to[x].push_back(y),to[y].push_back(x);
init(1,0);
dfs(1);
cout<<f[1];
return 0;
}
这里有一道据说类似的题,如果感兴趣可以做做。
区间 DP
区间 DP,就是指状态中含有一个区间的 DP,使用时通常需要满足可以快速加入元素或可以快速合并,大多数题都是从小区间转移到大区间。
因为合并区间时会枚举决策点,这个时候可以使用一些有关决策的 DP 优化,但是这目前不在我们的讨论范围之内。
如果用区间 DP 计数的时候,注意去重。
由于作者认为这个 DP 比较重要,所以塞了比较多题。
接下来就是例题时间了。
P7914 [CSP-S 2021] 括号序列
具体而言,小 w 定义“超级括号序列”是由字符
(、)、*组成的字符串,并且对于某个给定的常数 \(k\),给出了“符合规范的超级括号序列”的定义如下:
()、(S)均是符合规范的超级括号序列,其中S表示任意一个仅由不超过 \(\bf{k}\) 个字符*组成的非空字符串(以下两条规则中的S均为此含义);- 如果字符串
A和B均为符合规范的超级括号序列,那么字符串AB、ASB均为符合规范的超级括号序列,其中AB表示把字符串A和字符串B拼接在一起形成的字符串;- 如果字符串
A为符合规范的超级括号序列,那么字符串(A)、(SA)、(AS)均为符合规范的超级括号序列。- 所有符合规范的超级括号序列均可通过上述 3 条规则得到。
例如,若 \(k = 3\),则字符串
((**()*(*))*)(***)是符合规范的超级括号序列,但字符串*()、(*()*)、((**))*)、(****(*))均不是。特别地,空字符串也不被视为符合规范的超级括号序列。现在给出一个长度为 \(n\) 的超级括号序列,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用
?表示)。小 w 希望能计算出:有多少种将所有尚未确定的字符一一确定的方法,使得得到的字符串是一个符合规范的超级括号序列?\(1\leq k\leq n\leq 500\)。
Hint
如果不好去重,就多定义几个状态出来辅助 DP 来去掉去重这一步。
题解
这里讲一种不需要去重的 DP 方式。
首先我们可以预处理出那些区间是可以变成 S 的。
设 \(f_{i,j}\) 为该区间字符串是超级括号序列的方案数,\(g_{i,j}\) 代表该区间字符串为 SA(A 是超级括号序列)的方案数,\(h_{i,j}\) 代表该区间字符串为 AS 的方案数,\(w_{i,j}\) 代表该区间字符串是 () 或 (S) 或 (AS) 或 (SA) 的方案数。
首先看 \(g\) 怎么转移。我们肯定是枚举 S 的长度,然后再后边尝试接上一个 A,不难发现其实是不会有算重的情况的,\(h\) 也是类似。
然后考虑怎么转移 \(w\)。首先可以特判 () 和 (S) 的情况,然后 (AS) 和 (SA) 其实都可以直接通过 \(g\) 和 \(h\) 转移过来。
最后就是最难的 \(f\) 了。最简单的转移是 \(f_{i,j}\gets w_{i,j}\),然后我们考虑 ASB,发现其实可以直接 \(f_{i,j}\gets f_{i,k}\times g_{k+1,j}\),这样是不会重复的,因为 S 的起点在每次转移的时候都不同。最后我们考虑 AB,我们发现如果直接 \(f_{i,j}\gets f_{i,k}\times f_{k+1,j}\) 是不可行的,因为显然此时假如说这个区间存在一种由 \(k\) 个 (...) 用 AB 方式组合起来的方案,那么这样计算这种方案就被计算了 \(k-1\) 次。考虑每种方案只有一个最左边的 (...),所以 \(f_{i,j}\gets w_{i,k}\times f_{k+1,j}\) 就是正确的了(这里代码中写的是 \(f_{i,j}\gets f_{i,k}\times w_{k+1,j}\))。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
#define int long long
int n,k;
int S[502][502];
char s[505];
int f[505][505],g[505][505],h[505][505],whol[505][505];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++){
for(int j=i;j<=min(n,i+k-1);j++){
//[i,j]
if(s[j]=='*'||s[j]=='?')S[i][j]=1;
else break;
}
}
for(int i=1;i<n;i++){
if((s[i]=='?'||s[i]=='(')&&(s[i+1]=='?'||s[i+1]==')'))whol[i][i+1]=1;
for(int j=i+2;j<=min(n,i+k+1);j++){
if((s[i]=='?'||s[i]=='(')&&(s[j]=='?'||s[j]==')')&&S[i+1][j-1])whol[i][j]=1;
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int p=j;p<j+i-1;p++){
f[j][j+i-1]=(f[j][j+i-1]+whol[j][p]*(f[p+1][j+i-1]+g[p+1][j+i-1])%mod)%mod;
g[j][j+i-1]=(g[j][j+i-1]+S[j][p]*f[p+1][j+i-1])%mod;
h[j][j+i-1]=(h[j][j+i-1]+S[p+1][j+i-1]*f[j][p])%mod;
}
if((s[j]=='?'||s[j]=='(')&&(s[j+i-1]=='?'||s[j+i-1]==')'))whol[j][j+i-1]=(whol[j][j+i-1]+f[j+1][j+i-2]+g[j+1][j+i-2]+h[j+1][j+i-2])%mod;
f[j][j+i-1]=(f[j][j+i-1]+whol[j][j+i-1])%mod;
}
}
cout<<f[1][n];
return 0;
}
UVA1630 串折叠 Folding
折叠由大写字母组成的长度为 \(n\)(\(1\leqslant n\leqslant100\))的一个字符串,使得其成为一个尽量短的字符串,例如
AAAAAA变成6(A)。
这个折叠是可以嵌套的,例如NEEEEERYESYESYESNEEEEERYESYESYES会变成2(N5(E)R3(YES))。
多解时可以输出任意解。\(n\leq 100\)。
输出方案的题是逃避不了的/xk。
如果大家写挂了,可以先到这道题来检验 DP 的正确性。
题解
这题我直接写从最短的循环节转移就过了,然后我和 zfy 讨论能不能从最短的循环节转移过来,最后 zfy 说自己证出来可以,但是我不太知道原理。
这题其实比较简单。
设 \(f_{i,j}\) 为区间 \([i,j]\) 的答案,可以从枚举循环节转移,也可以两区间合并。
暴力枚举循环节复杂度是 \(O(n+\sum_{p|n}\frac{n}{p})\leq O(n\ln n)\),所以总复杂度是 \(O(n^3\ln n)\)。
方案的话,记录这个是从循环节还是区间转移过来的,记录决策点,最后 DFS 还原即可。
代码
#include<bits/stdc++.h>
using namespace std;
int dp[101][101],g[101][101];
char s[101],*ss=s+1;
const int SIG=1e5;
int _10[101];
string getans(int l,int r){
// cerr<<l<<" "<<r<<"\n";
if(!g[l][r]){
string tmp;
tmp.clear();
for(int i=l;i<=r;i++)tmp+=s[i];
return tmp;
}
if(g[l][r]>SIG){
string tmp;
tmp.clear();
tmp+=to_string((r-l+1)/(g[l][r]-SIG-l+1));
tmp+='(';
tmp+=getans(l,g[l][r]-SIG);
tmp+=')';
return tmp;
}
return getans(l,g[l][r])+getans(g[l][r]+1,r);
}
#define ull unsigned long long
ull hsh[105],_b[105];
const ull base=179;
ull gethsh(int l,int r){
return hsh[r]-hsh[l-1]*_b[r-l+1];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
for(int i=1;i<=9;i++)_10[i]=1;
for(int i=10;i<=100;i++)_10[i]=_10[i/10]+1;
_b[0]=1;
for(int i=1;i<=100;i++)_b[i]=_b[i-1]*base;
while(cin>>ss){
memset(g,0,sizeof g);
int n=strlen(ss);
for(int i=1;i<=n;i++)hsh[i]=hsh[i-1]*base+s[i]-'A'+1;
for(int i=1;i<=n;i++)for(int j=i;j<=n;j++)dp[i][j]=j-i+1;
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int k=j;k<j+i-1;k++){
if(dp[j][j+i-1]>dp[j][k]+dp[k+1][j+i-1]){
g[j][j+i-1]=k;
dp[j][j+i-1]=dp[j][k]+dp[k+1][j+i-1];
}
if(i%(k-j+1))continue;
//[j,k]
bool flag=1;
for(int o=j;o<=j+i-1&&flag;o+=k-j+1){
flag&=gethsh(j,k)==gethsh(o,o+k-j);
}
if(flag){
if(dp[j][j+i-1]>_10[i/(k-j+1)]+2+dp[j][k]){
g[j][j+i-1]=SIG+k;
dp[j][j+i-1]=_10[i/(k-j+1)]+2+dp[j][k];
}
}
}
}
}
// cout<<dp[1][n]<<"\n";
cout<<getans(1,n)<<"\n";
}
return 0;
}
有兴趣的可以再来做一道字符串压缩的题,这道题感觉比较有意思:[AGC020E] Encoding Subsets。
P4766 [CERC2014] Outer space invaders
来自外太空的外星人(最终)入侵了地球。保卫自己,或者解体,被他们同化,或者成为食物。迄今为止,我们无法确定。
外星人遵循已知的攻击模式。有 \(N\) 个外星人进攻,第 \(i\) 个进攻的外星人会在时间 \(a_i\) 出现,距离你的距离为 \(d_i\),它必须在时间 \(b_i\) 前被消灭,否则被消灭的会是你。
你的武器是一个区域冲击波器,可以设置任何给定的功率。如果被设置了功率 \(R\),它会瞬间摧毁与你的距离在 \(R\) 以内的所有外星人(可以等于),同时它也会消耗 \(R\) 单位的燃料电池。
求摧毁所有外星人的最低成本(消耗多少燃料电池),同时保证自己的生命安全。
\(1\leq n\leq 300\)。
Hint
如果发现不好想转移的话,可以想想什么是这个区间一定会执行的操作。
题解
首先不难发现这个时间是可以离散化的,这样我们就可以设 \(f_{i,j}\) 是消灭生存区间的两个端点都在 \([i,j]\) 内的最低成本。
直接想转移可能比较困难。考虑什么东西是这个区间的答案一定含有的。
不难发现想要消灭这个区间内的所有外星人,最优情况下我们一定有一次选择了 \(R=\max_i d_i\) 的功率进行消灭。我们可以在 \(O(n)\) 的时间内找到这个外星人。
因为我们一定会在这个外星人的生存区间中的一个点发动 \(R=\max_id_i\) 的攻击,所以我们可以枚举在这个生存区间的哪个位置发动这个攻击。因为这是整个区间的最大功率,所以它一定也会消灭所有生存区间跨过这个位置的外星人,这个时候就只剩下左右两个区间内的外星人了。我们可以列出方程式(设 \(id\) 是距离最远的那个外星人的编号):
\[f_{l,r}=d_{id}+\max_{k\in[l_{id},r_{id}]}(f_{l,k-1}+f_{k+1,r}) \]时间复杂度 \(O(n^3)\)。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n,dis[505],l[505],r[505],maxid[605][605],dp[605][605];
int num[605],kcnt;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T;
while(T--){
cin>>n;
kcnt=0;
memset(maxid,0,sizeof maxid);
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i]>>dis[i];
num[++kcnt]=l[i];
num[++kcnt]=r[i];
}
sort(num+1,num+kcnt+1);
kcnt=unique(num+1,num+kcnt+1)-num-1;
for(int i=1;i<=n;i++){
l[i]=lower_bound(num+1,num+kcnt+1,l[i])-num;
r[i]=lower_bound(num+1,num+kcnt+1,r[i])-num;
}
for(int i=1;i<=kcnt;i++){
for(int j=i+1;j<=kcnt;j++){
for(int p=1;p<=n;p++){
if(l[p]>=i&&r[p]<=j)if(dis[p]>dis[maxid[i][j]])maxid[i][j]=p;
}
}
}
for(int i=1;i<=kcnt;i++)for(int j=i+1;j<=kcnt;j++)dp[i][j]=1e9;
for(int i=2;i<=kcnt;i++){
for(int j=1;j<=kcnt-i+1;j++){
//[j,j+i-1]
int id=maxid[j][j+i-1];
if(!id){dp[j][j+i-1]=0;continue;}
for(int k=l[id];k<=r[id];k++){
dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][k-1]+dp[k+1][j+i-1]+dis[id]);
}
}
}
cout<<dp[1][kcnt]<<"\n";
}
return 0;
}
选做习题:P3592 [POI2015] MYJ
P2339 [USACO04OPEN] Turning in Homework G
贝茜有 $ C $ ( $ 1 \leq C \leq 1000 $ ) 门科目的作业要上交,之后她要去坐巴士和奶牛同学回家。
每门科目的老师所在的教室排列在一条长为 $ H $ ( $ 1 \leq H \leq 1000 $ ) 的走廊上,他们只在课后接收作业,交作业不需要时间。贝茜现在在位置 0,她会告诉你每个教室所在的位置,以及走廊出口的位置。她每走 1 个单位的路程,就要用 1 秒。她希望你计算最快多久以后她能交完作业并到达出口。
Hint
这道题不难发现先交一个区间的作业不能作为状态,因为有可能在等区间内的老师下课的时候可以跑到区间外交作业。那有没有可能先不交一个区间的作业作为状态呢?
题解
设 \(f_{l,r,0/1}\) 为区间 \([l,r]\) 的作业还没交,当前在 \(l\) 位置还是 \(r\) 位置的最小时间。
非常反直觉的状态设计对吧?如何证明其包含最优解呢?考虑把最优解倒过来看,这样我们可以把下课变成上课,即需要在上课之前交作业。这个时候的 DP 就是枚举交了哪个区间的作业,现在在该区间的左端点还是右端点,求最小时间。把这个 DP 再倒过来就变成上面的状态了,两个都是最小时间没有问题,因为这两个最小时间加起来就等于最优解时间。
另一种理解方式就是,如果 \(l+1\) 位置的作业之前没交,你移动到 \(r\) 之后要走回来交;如果 \(l+1\) 位置的作业之前可以交,那么完全可以先移动到 \(l+1\) 之后再移动。所以转移是完整的。
剩下的转移也非常简单了,从大区间转移到小区间,枚举上次移动是从左边还是右边移动过来即可。注意没有下课的时候需要等待,在倒过来的 DP 中这一步就代表这个地方已经上课了,需要增加最优解时间来使得其延后上课。
时间复杂度 \(O(n^2)\)。
如果实在理解不了,你也可以在外面套个二分,因为答案具有单调性。然后倒着 DP 检验即可,时间复杂度 \(O(n^2\log V)\)。
代码
#include<bits/stdc++.h>
using namespace std;
int n,h,b;
int x[1005],t[1005];
int id[1005];
int dp[1005][1005][2];
int main(){
ios::sync_with_stdio(0);
cin>>n>>h>>b;
h++;
b++;
int acth=0;
for(int i=1;i<=n;i++){
cin>>x[i]>>t[i];
x[i]++;
acth=max(x[i],acth);
if(t[id[x[i]]]<t[i])id[x[i]]=i;
}
h=acth;
memset(dp,0x3f,sizeof dp);
dp[1][h][0]=0;
dp[1][h][1]=h-1;
for(int i=h-1;i>=1;i--){
for(int j=1;j<=h-i+1;j++){
//[j,j+i-1]
dp[j][j+i-1][1]=min(max(dp[j][j+i][1],t[id[j+i]])+1,max(dp[j-1][j+i-1][0],t[id[j-1]])+i);
dp[j][j+i-1][0]=min(max(dp[j-1][j+i-1][0],t[id[j-1]])+1,max(dp[j][j+i][1],t[id[j+i]])+i);
}
}
int ans=1e9;
for(int i=1;i<=h;i++){
ans=min(ans,max(dp[i][i][0],t[id[i]])+abs(b-i));
}
cout<<ans;
return 0;
}
P9746 「KDOI-06-S」合并序列
注意:该题为选做题。
给定一个长度为 \(n\) 的序列 \(a_1,a_2,\ldots a_n\)。
你可以对这个序列进行若干(可能为 \(0\))次操作。在每次操作中,你将会:
选择三个正整数 \(i<j<k\),满足 \(a_i\oplus a_j\oplus a_k=0\) 且 \(k\) 的值不超过此时序列的长度。记 \(s=a_i\oplus a_{i+1}\oplus \cdots\oplus a_k\)。
然后,删除 \(a_i\sim a_k\),并在原来这 \(k-i+1\) 个数所在的位置插入 \(s\)。注意,此时序列 \(a\) 的长度将会减少 \((k-i)\)。
请你判断是否能够使得序列 \(a\) 仅剩一个数,也就是说,在所有操作结束后 \(a\) 的长度为 \(1\)。若可以,你还需要给出一种操作方案。
\(n\leq 500\),\(a_i<512\)。
Hint
大家可以尝试多建几个数组来在 DP 的时候分步合并转移。
题解
以下令 \(V=O(n)\)。
转换一下题意,设 \(f_{l,r}\) 为区间 \([l,r]\) 是否可以被消成一个数,如果需要让 \(f_{l,r}=1\),那么我们需要满足存在 \(l\leq a<b\leq c<d\leq r\),使得 \(f_{l,a}=f_{b,c}=f_{d,r}=1\) 且 \(\bigoplus_{i\in[l,a]\cup[b,c]\cup[d,r]}a_i=0\)。
首先肯定可以先 \(O(n^2)\) 预处理出所有区间的异或和,然后直接暴力枚举 \(a,b,c,d\),时间复杂度 \(O(n^6)\)。
我们的目标是 \(O(n^3)\),所以我们要把这 \(4\) 个维度的枚举变成 \(1\) 个维度的枚举,想到分步转移。假设最后枚举 \(d\),我们可以设 \(g_{l,p}\) 代表满足 \(\bigoplus_{i\in[l,a]\cup[b,c]}=p\) 的最小的 \(c\)。这个时候还需要枚举 \(2\) 个维度,于是继续压。因为求的已经是最小的 \(c\) 了,为了方便就只能枚举 \(a\)。于是我们再设 \(h_{l,p}\) 表示满足 \(\bigoplus_{i\in[l+1,c]}=p\) 的最小的 \(c\),这样我们就可以 \(O(n)\) 转移了。
\[\forall l,r,s=\bigoplus_{i=l}^ra_{i}\\ h_{i-1,s}\gets r(i\leq l)\\ g_{l,p}\gets h_{r,s\oplus p}\\ f_{l,r}\gets [g_{l,\oplus_{i=k}^ra_{i}}<k] \]输出方案的时候,转移 \(f\) 的时候记录 \(d\),转移 \(g\) 的时候记录 \(a\),转移 \(h\) 的时候记录 \(b\) 即可。时间复杂度 \(O(n^3)\)。
因为这题是可以通过 \(>l\) 的信息转移到 \(l\) 上,所以转移顺序应该是倒序枚举 \(l\) 再枚举 \(r\),根据第二个转移,我们需要顺序枚举 \(r\),因为 \(>r\) 的右端点一定不会贡献 \(\leq r\) 的值。
交一发之后发现 T 在了 hack 数据,我们需要减小常数。
我们发现第一个转移 \(i\leq l-1\) 的部分可以变成最后在转移完 \(l\) 的时候进行 \(h_{l-1,p}\gets h_{l,p}\)。这样能减少 \(\frac{1}{3}\) 左右的常数,可以通过。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n;
int a[505];
int xors[505][505];
int h[505][515],g[505][515];
bool f[505][505];
int posh[505][515],posg[505][515],posf[505][505];
const int M=512;
struct op{
int i,j,k;
};
vector<op> ans;
void getans(int l,int r){
// cerr<<l<<" "<<r<<" "<<f[l][r]<<"\n";
if(l==r)return;
int d=posf[l][r];
int a=posg[l][xors[d][r]];
int b=posh[a][xors[d][r]^xors[l][a]];
int c=g[l][xors[d][r]];
getans(d,r);
getans(b,c);
getans(l,a);
ans.push_back((op){l,b-(a-l),d-(a-l)-(c-b)});
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T;
int n;
while(T--){
memset(h,0x3f,sizeof h);
memset(g,0x3f,sizeof g);
memset(f,0,sizeof f);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
int tmp=0;
for(int j=i;j<=n;j++){
tmp^=a[j];
xors[i][j]=tmp;
}
}
for(int i=1;i<=n;i++)f[i][i]=1;
for(int i=n;i>=1;i--){
int l=i;
for(int j=i;j<=n;j++){
int r=j;
int tmp=0;
for(int k=r;k>l;k--){
tmp^=a[k];
if(g[l][tmp]<k&&f[k][r]){
f[l][r]=1;
posf[l][r]=k;
break;
}
}
if(f[l][r]){
if(h[l-1][xors[l][r]]>r)h[l-1][xors[l][r]]=r,posh[l-1][xors[l][r]]=l;
for(int i=0;i<M;i++){
if(g[l][i]>h[r][i^xors[l][r]])g[l][i]=h[r][i^xors[l][r]],posg[l][i]=r;
}
}
}
for(int i=0;i<M;i++)if(h[l-1][i]>h[l][i])h[l-1][i]=h[l][i],posh[l-1][i]=posh[l][i];
}
if(!f[1][n])cout<<"Shuiniao\n";
else{
// cerr<<f[2][4]<<"\n";
cout<<"Huoyu\n";
getans(1,n);
cout<<ans.size()<<"\n";
for(auto p:ans)cout<<p.i<<" "<<p.j<<" "<<p.k<<"\n";
ans.clear();
}
}
return 0;
}
P3607 [USACO17JAN] Subsequence Reversal P
给你一个长度为 \(n\) 的序列 \(a\),求翻转一个子序列之后最长的不下降子序列长度。
\(n\leq 50,a_i\leq 50\)。
Hint
尝试转化(或拆)一下翻转子序列这个操作呢?
题解
把翻转子序列这个操作拆成交换几个元素对,这些元素对满足两两均有包含关系。根据这个 包含关系,我们知道这道题是显然可以区间 DP 的。
所以我们设 \(f_{l,r,L,R}\) 为区间 \([l,r]\) 中的所有元素值在 \([L,R]\) 的最长子序列长度。枚举翻转和扩展的所有情况,转移较为容易,这里就不展开叙述。注意几个点就行了:
- 枚举翻转的时候不止可以转移两边都能扩展的子序列。
- 注意在 \([L,R]\) 内,所以这里要取一个类似于二维前缀 \(\max\) 的东西。
代码
#include<bits/stdc++.h>
using namespace std;
int f[55][55][55][55];
int n;
const int m=50;
int a[55];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
for(int l=1;l<=m;l++){
for(int r=1;r<=m;r++){
if(l<=a[i]&&r>=a[i])f[i][i][l][r]=1;
}
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
//[j,j+i-1]
if(a[j]>a[j+i-1]){
//swap j j+i-1
f[j][j+i-1][a[j+i-1]][a[j]]=2+f[j+1][j+i-2][a[j+i-1]][a[j]];
}
for(int p=max(a[j],a[j+i-1])+1;p<=m;p++)f[j][j+i-1][a[j+i-1]][p]=1+f[j+1][j+i-2][a[j+i-1]][p];
for(int p=min(a[j],a[j+i-1])-1;p>=1;p--)f[j][j+i-1][p][a[j]]=1+f[j+1][j+i-2][p][a[j]];
for(int p=1;p<=m;p++){
for(int l=1;l<=m-p+1;l++){
int r=l+p-1;
//[j,j+i-1],[l,r]
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j+1][j+i-1][l][r]);
if(l<=a[j]&&a[j]<=r)f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j+1][j+i-1][a[j]][r]+1);
// if(j==1&&j+i-1==2)cerr<<j<<" "<<j+i-1<<" "<<l<<" "<<r<<" "<<f[j][j+i-1][l][r]<<" "<<a[j]<<"\n";
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-2][l][r]);
if(r>=a[j+i-1]&&l<=a[j+i-1])f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-2][l][a[j+i-1]]+1);
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-1][l][r-1]);
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-1][l+1][r]);
}
}
}
}
cout<<f[1][n][1][m];
return 0;
}
P10041 [CCPC 2023 北京市赛] 史莱姆工厂
有 \(n\) 个史莱姆排成一行,其中第 \(i\) 个的颜色为 \(c_i\),质量为 \(m_i\)。
你可以执行任意次把一个史莱姆的质量增加 \(1\) 的操作,需要花费 \(w\) 的价钱。
但是一旦史莱姆的质量达到 \(k\) 或以上,就会变得不稳定而必须在下一次操作之前被卖掉。你只能卖出质量大于等于 \(k\) 的史莱姆。根据市场价,卖掉一个质量为 \(i\) 的史莱姆可以得到 \(p_i\) 的收入。保证 \(p_i-p_{i-1}<w\)。但不保证 \(p_i\) 单调不降。
卖掉一个史莱姆之后,它两边的史莱姆会被挤压继而靠在一起。如果这两个史莱姆颜色相同,那么就会互相融合成一个史莱姆,其质量是二者的质量之和。这个新的史莱姆也有可能需要被卖掉从而接着进行这个过程。
你想知道卖掉所有史莱姆最多可以净赚多少。
\(n\leq 150\),\(k\leq 10\)。
区间 DP 魔王。(仅凭洛谷评级来看)
Hint
对于一个区间,想想最后一个操作会发生在哪里,然后尝试把这个操作钦定发生在一个区间内的特殊的位置。
题解
参考了部分 Hanghang 的题解,但是 Hanghang 的题解中有些错误,怎么回事捏。
考虑对于一个区间,它的消除一定是通过几个不同的区间一起消除,或者是最后左右端点合并进行消除。所以我们一定能重排操作序列,使得这个区间的最后一次操作在左右端点处,这样方便于我们设计状态。因为这道题左右端点其实是差不多等价的,所以我们就定义 \(f_{l,r}\) 为消完区间 \([l,r]\) 之后的最大利润, \(fl_{l,r,p}\) 表示区间 \([l,r]\) 中消完最后剩下一个颜色为 \(c_{l}\),重量为 \(p\) 的史莱姆的最大利润,需要保证中间的过程中,最左侧的史莱姆没有被消掉。
最后一次的消除有两种情况,第一种是花钱加重量后消除,第二种是两个同颜色的撞在一起之后可以直接消除。我们先来看第一种。
我们有一个比较显然的转移:
\[f_{l,r}\gets f_{l,k}+fl_{k+1,r,q}+p_{m}-(m-q)w \]\(fl\) 的转移也较容易。首先有 \(fl_{l,r,m_l}\gets f_{l+1,r}\)。然后因为最左侧史莱姆没有消掉,所以有 \(fl_{l,r,p}\gets f_{l+1,k}+fl_{k+1,r,p-m_l}(c_{k+1}=c_l)\)。(为什么没有 \(fl_{l,k,p}+f_{k+1,r}\):上面那个式子显然已经包含了这个东西)注意上述两个转移不能有边界上的合并颜色,下面的转移同样需要注意,后面就不赘述这一部分了。
接下来我们来转移第二种情况。采用分步转移的思想(因为再定义一个 \(fr\),然后枚举两个颜色相等点转移的复杂度至少有一个 \(O(n^4)\),无法通过),设 \(g_{l,r,p}\) 为合并完 \([l,r)\) 之后,剩下的物品颜色为 \(c_r\),重量为 \(p\)。
所以我们显然有:\(f_{l,r}\gets g_{l,k,u}+fl_{k,r,q}+p_{u+q}\)。接下来转移 \(g\) 就大功告成了。而 \(g\) 其实和 \(fl\) 差不多:
\[g_{l,r,p}\gets f_{l,k}+fl_{k+1,r-1,p}(c_{k+1}=c_r) \]总时间复杂度 \(O(n^3k^2)\)。
代码
#include<bits/stdc++.h>
using namespace std;
int n,k;
#define ll long long
ll p[21],w;
ll f[155][155],fl[155][155][11],fr[155][155][11],g[155][155][11];
void renew(ll &x,ll y){
if(x<y)x=y;
return;
}
int c[155],m[155];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k>>w;
for(int i=1;i<=n;i++)cin>>c[i];
for(int j=1;j<=n;j++)cin>>m[j];
for(int i=k;i<=2*k-2;i++)cin>>p[i];
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
f[i][j]=-1e18;
for(int o=1;o<=k;o++)fl[i][j][o]=fr[i][j][o]=g[i][j][o]=-1e18;
}
}
for(int i=1;i<=n;i++)f[i][i]=p[k]-w*(k-m[i]),fl[i][i][m[i]]=fr[i][i][m[i]]=0;
for(int i=2;i<=n;i++){
for(int l=1;l<=n-i+1;l++){
int r=l+i-1;
fl[l][r][m[l]]=f[l+1][r];
fr[l][r][m[r]]=f[l][r-1];
for(int t=l+1;t<=r;t++)if(c[t]==c[l])for(int o=m[l]+1;o<k;o++)renew(fl[l][r][o],f[l+1][t-1]+fl[t][r][o-m[l]]);
// for(int t=l;t<=r;t++)if(c[t]==c[r])for(int o=m[r]+1;o<k;o++)renew(fr[l][r][o],fr[l][t][o-m[r]]+f[t+1][r-1]);
for(int t=l;t<=r;t++)if(c[l-1]!=c[t]&&c[t]!=c[r+1])for(int o=1;o<k;o++)renew(f[l][r],f[l][t-1]+fl[t][r][o]+p[k]-w*(k-o));
for(int t=l;t<=r;t++)if(c[t]==c[r+1])for(int o=1;o<k;o++)renew(g[l][r][o],fl[t][r][o]+f[l][t-1]);
for(int t=l+1;t<=r;t++)if(c[t]!=c[l-1]&&c[t]!=c[r+1])
for(int o1=1;o1<k;o1++)for(int o2=1;o2<k;o2++)if(o1+o2>=k)renew(f[l][r],g[l][t-1][o1]+fl[t][r][o2]+p[o1+o2]);
}
}
cout<<f[1][n];
return 0;
}
背包 DP
背包 DP,顾名思义,即使用 DP 的思想解决把物品放到背包里的物品。想必大家对 01 背包,完全背包,多重背包,分组背包都掌握了。所以我们板题就不放了。
依赖性背包大多是树形背包,DAG 上的依赖背包作者不会,如果读者会的话可以私信作者。
有一些板题,我看大家好像没怎么做,这里还是浅浅说说吧。
一些板题
板题:P1064 [NOIP2006 提高组] 金明的预算方案
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 \(n\) 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
主件 附件 电脑 打印机,扫描仪 书柜 图书 书桌 台灯,文具 工作椅 无 如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 \(0\) 个、\(1\) 个或 \(2\) 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 \(n\) 元。于是,他把每件物品规定了一个重要度,分为 \(5\) 等:用整数 \(1 \sim 5\) 表示,第 \(5\) 等最重要。他还从因特网上查到了每件物品的价格(都是 \(10\) 元的整数倍)。他希望在不超过 \(n\) 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 \(j\) 件物品的价格为 \(v_j\),重要度为 \(w_j\),共选中了 \(k\) 件物品,编号依次为 \(j_1,j_2,\dots,j_k\),则所求的总和为:
\(v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}\)。
总物品个数为 \(m\),请你帮助金明设计一个满足要求的购物单。
对于全部的测试点,保证 \(1 \leq n \leq 3.2 \times 10^4\),\(1 \leq m \leq 60\),\(0 \leq v_i \leq 10^4\),\(1 \leq p_i \leq 5\),\(0 \leq q_i \leq m\),答案不超过 \(2 \times 10^5\)。
题解
这题看样子像一个依赖性背包问题,但是因为只可能有两个附件,而且附件没有其他附件,所以其实可以对每个主件讨论选不选附件,选多少附件,情况数较少。
把一个主件的所有情况分为一组,对全局做一个分组背包即可。
时间复杂度为 \(O(nm)\)。
对于大家来说过于简单,就不贴代码了。
习题,板题:P1941 [NOIP2014 提高组] 飞扬的小鸟
较为板子的题:P1417 烹调方案
一共有 \(n\) 件食材,每件食材有三个属性,\(a_i\),\(b_i\) 和 \(c_i\),如果在 \(t\) 时刻完成第 \(i\) 样食材则得到 \(a_i-t\times b_i\) 的美味指数,用第 \(i\) 件食材做饭要花去 \(c_i\) 的时间。
众所周知,gw 的厨艺不怎么样,所以他需要你设计烹调方案使得在总花费时间小于等于 \(T\) 时美味指数最大。
\(n\leq 50\),其他数字均小于 \(10^5\)。
据说是泛化物品的一道题。随机大法好。
题解
这个题如果没有那个 \(a_{i}-t\times b_{i}\) 的美味指数限制,那就是一个显然的 01 背包问题。但是因为结束时间改变会导致权值改变,所以显然不能把所有物品看做等价。
因为从时间上枚举会导致物品算重,所以还是只能使用类似于背包的方法加入物品。我们尝试对于两个物品在最优解中的顺序进行贪心。
使用 exchange arguments 思想,考虑我们把最优顺序的两个物品交换顺序,我们发现只会有这两个物品受到影响,设这两个物品为 \(1\) 号和 \(2\) 号,\(1\) 号原来在前面,下面我们列出不等式:
\[\begin{aligned} a_1-tb_1+a_2-(t+c_1)b_2&\geq a_2-tb_2+a_1-(t+c_2)b_1\\ -c_1b_2&\geq -c_2b_1\\ c_1b_2&\leq c_2b_1\\ \frac{c_1}{b_1}&\leq\frac{c_2}{b_2} \end{aligned} \]我们发现,这个东西可以变成一个每个元素可以算出来的值的比较,所以我们可以直接对这个值进行排序以得到最优的顺序,其他的就交给 01 背包就行了。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n,a[51],b[51],c[51];
long long dp[100005];
int id[51];
bool cmp(const int &x,const int &y){
return 1ll*c[x]*b[y]<1ll*b[x]*c[y];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T>>n;
for(int i=1;i<=n;i++)cin>>a[i],id[i]=i;
for(int i=1;i<=n;i++)cin>>b[i];
for(int i=1;i<=n;i++)cin>>c[i];
sort(id+1,id+n+1,cmp);
for(int i=1;i<=n;i++){
for(int j=T;j>=c[id[i]];j--){
dp[j]=max(dp[j],dp[j-c[id[i]]]+a[id[i]]-1ll*j*b[id[i]]);
}
}
long long ans=0;
for(int i=1;i<=T;i++)ans=max(ans,dp[i]);
cout<<ans;
return 0;
}