朴素 DP
[ABC301F] Anti-DDoS
题意
定义形如 DDoS 的序列为类 DDoS 序列,其中 DD 表示两个相同的任意大写字母,o 表示任意小写字母,S 表示任意大写字母。
给定一个由大小写字母和 ? 组成的序列 \(S\),问有多少种将 ? 替换为大小写字母的方案可以使 \(S\) 不含有任何一个类 DDoS 子序列,答案对 \(998244353\) 取模。
\(4 \le \left|S\right| \le 3 \times 10^5\)。
解法
这是上一道例题的变式。
这一道题因为是对不含类 DDoS 子序列的方案计数,所以为了方便,我们设 \(f_{i,j}\) 是前 \(i\) 位中没有类 DDoS 子序列中的前 \(j+2\) 位的方案数。显然答案就是 \(f_{n,2}\)。
首先我们考虑如何计算 \(f_{i,0}\),即使前 \(i\) 位中不含两个相同大写字母的方案数。考虑假设前 \(i\) 位有 \(m\) 个 ?,有 \(k\) 种大写字母。注意到如果这 \(k\) 种大写字母的总个数不为 \(k\),那么此时方案数一定为 \(0\)。否则我们可以在 \(m\) 个 ? 选取 \(0\sim k\) 个选择大写字母,其余选择小写字母,这样我们可以列出式子:
然后考虑如何计算 \(f_{i,1}\) 和 \(f_{i,2}\)。对于不存在 DDo 的方案数,我们发现如果一个位置是大写字母,那么这里我们就只需要保证之前不存在 DDo 就行了;而如果一个位置是小写字母,我们这里则要保证之前不存在 DD;如果是 ? 的话,等于说这里任意小写或大写字母都可以填,于是有转移式:
对 \(f_{i,2}\) 的转移类似。
这样我们就在 \(O(n|\Sigma|)\) 的时间复杂度内解决了此题。
代码
#include<bits/stdc++.h>
using namespace std;
string s;
#define int long long
int f[300005][5];
int frac[300005],ifrac[300005],_26[300005];
const int mod=998244353;
int ksm(int a,int b){
if(!b)return 1;
return (b&1?a:1)*ksm(a*a%mod,b/2)%mod;
}
int vis[27],lftc=26;
int A(int a,int b){
if(a<b)return 0;
return frac[a]*ifrac[a-b]%mod;
}
int C(int a,int b){
if(a<b)return 0;
return frac[a]*ifrac[a-b]%mod*ifrac[b]%mod;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s;
int siz=s.size();
frac[0]=_26[0]=1;
int lim=max(26ll,siz);
for(int i=1;i<=lim;i++)frac[i]=frac[i-1]*i%mod,_26[i]=_26[i-1]*26%mod;
ifrac[lim]=ksm(frac[lim],mod-2);
for(int i=lim-1;i>=0;i--)ifrac[i]=ifrac[i+1]*(i+1)%mod;
int cntq=0;
f[0][0]=f[0][1]=f[0][2]=1;
for(int i=1;i<=siz;i++){//DD
if(s[i-1]=='?')cntq++;
else if(s[i-1]>='A'&&s[i-1]<='Z'){
if(vis[s[i-1]-'A'+1])break;
else vis[s[i-1]-'A'+1]=1,lftc--;
}
int &p=f[i][0];
for(int j=min(lftc,cntq);j>=0;j--){
p=(p+C(cntq,j)*A(lftc,j)%mod*_26[cntq-j]%mod)%mod;
// cout<<j<<" "<<cntq<<" "<<lftc<<" "<<C(cntq,j)<<" "<<A(lftc,j)<<" "<<frac[26]<<" "<<p<<"\n";
}
}
// cout<<"\n";
for(int i=1;i<=siz;i++){//DDo
if(s[i-1]=='?')f[i][1]=(26ll*f[i-1][0]%mod+26ll*f[i-1][1]%mod)%mod;
else if(s[i-1]>='a'&&s[i-1]<='z')f[i][1]=f[i-1][0];
else f[i][1]=f[i-1][1];
}
for(int i=1;i<=siz;i++){
if(s[i-1]=='?')f[i][2]=(26ll*f[i-1][1]%mod+26ll*f[i-1][2]%mod)%mod;
else if(s[i-1]>='a'&&s[i-1]<='z')f[i][2]=f[i-1][2];
else f[i][2]=f[i-1][1];
}
cout<<f[siz][2];
return 0;
}
P2224 [HNOI2001] 产品加工
题意
某加工厂有 A、B 两台机器,来加工的产品可以由其中任何一台机器完成,或者两台机器共同完成。由于受到机器性能和产品特性的限制,不同的机器加工同一产品所需的时间会不同,若同时由两台机器共同进行加工,所完成任务又会不同。
某一天,加工厂接到 \(n\) 个产品加工的任务,每个任务的工作量不尽一样。
你的任务就是:已知每个任务在 A 机器上加工所需的时间 \(t_1\),B 机器上加工所需的时间 \(t_2\) 及由两台机器共同加工所需的时间 \(t_3\),请你合理安排任务的调度顺序,使完成所有 \(n\) 个任务的总时间最少。
\(1\leq n\leq 6\times 10^3\),\(0\leq t_1,t_2,t_3\leq 5\)。
解法
和上一道题有一些相似之处。
注意到题面没有说非要按顺序完成这些任务,直接按顺序加入元素显然可能会导致等待,这样不同顺序会有不同的 DP 结果,所以我们需要一种不导致等待或者可以按某个顺序 DP 的 DP 方式。
考虑假设这个时候我们已经通过 DP 算出了一个前 \(i\) 个元素的调度顺序。
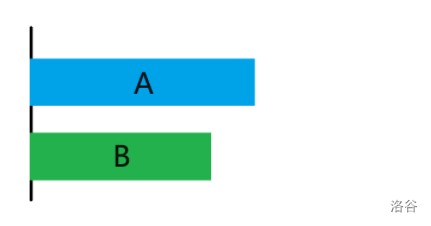
这个时候我们对 A 或 B 设置一个单独的任务,并不会产生额外的工作时间变化。
但是我们对 A,B 设置一个一起做的任务,我们发现此时 B 就需要被迫等待 A 做完剩下的才能和 A 一起做。这个时候我们把这个任务插到开头,发现就没有这个等待的时间了,这时因为没有多余时间,所以一定最优。
因为最优情况下一定没有等待时间,所以原问题就变成了有一些任务,选一些给 A 做,选一些给 B 做,再选一些让它们一起做,求两个机器运作的时间的最大值的最小值,这样每个元素都是独立的,加入时不受前面或后面元素的影响,这样就能 DP 了。
所以我们设 \(f_{i,j}\) 为前 \(i\) 个元素中,A 机器运行了 \(j\) 时间,B 机器运行的最小时间。转移是简单的,就讨论这个任务是由 A 做还是由 B 做还是一起做。有:
\[f_{i,j}\gets f_{i-1,j-t_1}\\ f_{i,j}\gets f_{i-1,j}+t_2\\ f_{i,j}\gets f_{i-1,j-t_3}+t_3 \]这样我们能在 \(O(nV)\) 时间复杂度内解决这个问题,其中 \(V=5n\)。
代码
#include<bits/stdc++.h>
using namespace std;
int n;
const int M=3e4;
int dp[2][M+5];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int now=1,ed=0,t1,t2,t3;
memset(dp[0],0x3f,sizeof dp[0]);
dp[0][0]=0;
cin>>n;
for(int i=1;i<=n;i++){
cin>>t1>>t2>>t3;
memset(dp[now],0x3f,sizeof dp[now]);
for(int j=0;j<=M;j++){
if(t1&&j>=t1)dp[now][j]=min(dp[now][j],dp[ed][j-t1]);
if(t2)dp[now][j]=min(dp[now][j],dp[ed][j]+t2);
if(t3&&j>=t3)dp[now][j]=min(dp[now][j],dp[ed][j-t3]+t3);
}
swap(now,ed);
}
int ans=1e9;
for(int i=0;i<=M;i++)ans=min(ans,max(i,dp[ed][i]));
cout<<ans;
return 0;
}
区间 DP
P2470 [SCOI2007] 压缩
题意
给一个由小写字母组成的字符串,我们可以用一种简单的方法来压缩其中的重复信息。压缩后的字符串除了小写字母外还可以(但不必)包含大写字母R与M,其中M标记重复串的开始,R重复从上一个M(如果当前位置左边没有M,则从串的开始算起)开始的解压结果(称为缓冲串)。
bcdcdcdcd 可以压缩为 bMcdRR,下面是解压缩的过程:
| 已经解压的部分 | 解压结果 | 缓冲串 |
|---|---|---|
| b | b | b |
| bM | b | . |
| bMc | bc | c |
| bMcd | bcd | cd |
| bMcdR | bcdcd | cdcd |
| bMcdRR | bcdcdcdcd | cdcdcdcd |
\(n\leq 50\)。
解法
和上道题一样的压缩字符串类的题。
其实这题可以加一个输出方案,这样的话这题就是一个作者认为非常好的例题。
因为这题要处理 M,所以我们可以设 \(f_{i,j}\) 为区间 \([i,j]\) 可以用 R 字符压缩的最短长度。
这里就有两个转移,第一个是 \(f_{i,j}\gets f_{i,i+\frac{j-i+1}{2}-1}+1\),压缩一半。
第二个是合并两个区间,我们有 \(f_{i,j}\gets f_{i,k}+(j-k+1)\),因为第二个区间不能有 R。
然后我们考虑把所有区间的 \(f\) 用另外一个 DP 合并起来,设 \(g_{i}\) 为前 \(i\) 个元素的压缩后最短长度,显然有 \(g_{i}\gets g_j+f_{j+1,i}+1\),\(1\) 是给前面加的 M 加的。
这两个方程式都很像能 DP 优化的样子,如果胡出来这个优化的可以私信作者。
UPD:作者胡了一个 \(O(n^2)\) 的扫描一遍 + 单调栈的做法,但是这题 \(n\leq 50\) 随便过。
最后答案就是 \(g_{1,n}-1\)。
代码
#include<bits/stdc++.h>
using namespace std;
char s[55],*ss=s+1;
int dp[55][55];
int f[55];
#define ull unsigned long long
ull hsh[55];
const ull base=179;
ull _b[55];
ull gethsh(int l,int r){
return hsh[r]-hsh[l-1]*_b[r-l+1];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>ss;
int n=strlen(ss);
_b[0]=1;
for(int i=1;i<=n;i++)hsh[i]=hsh[i-1]*base+s[i]-'a'+1,_b[i]=_b[i-1]*base;
for(int i=1;i<=n;i++)f[i]=1e9;
memset(dp,0x3f,sizeof dp);
for(int i=1;i<=n;i++)dp[i][i]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int k=j;k<j+i-1;k++){
dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][k]+(j+i-1)-k);
}
if(i%2==0){
if(gethsh(j,j+i/2-1)==gethsh(j+i/2,j+i-1))dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][j+i/2-1]+1);//...R
}
}
}
// cerr<<dp[1][4]<<" "<<gethsh(1,2)<<" "<<gethsh(3,4)<<"\n";
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
f[i]=min(f[i],f[j]+dp[j+1][i]+1);
}
}
cout<<f[n]-1;
return 0;
}
P3592 [POI2015] MYJ
题意
有 \(n\) 家洗车店从左往右排成一排,每家店都有一个正整数价格 \(p_i\)。有 \(m\) 个人要来消费,第 \(i\) 个人会驶过第 \(a_i\) 个开始一直到第 \(b_i\) 个洗车店,且会选择这些店中最便宜的一个进行一次消费。但是如果这个最便宜的价格大于 \(c_i\),那么这个人就不洗车了。请给每家店指定一个价格,使得所有人花的钱的总和最大。
\(n\leq 50,m\leq 4000\)。
解法
和上一道题基本一样,而且要输出方案,所以是选做。
离散化 \(c_i\),设 \(f_{l,r,p}\) 为区间 \([l,r]\) 的定价都不小于 \(p\) 的时候,对于行驶区间完全包含于 \([l,r]\) 的人的花费最大值。
考虑随意指定这个区间的一个位置,钦定其定价为 \(p\),因为其余定价都不小于 \(p\),所以行驶跨过该位置的人如果要花费就可以在这里花费。所以我们有:
\[f_{l,r,p}=\max_{pos\in[l,r]}(p\times cnt_{pos,p}+f_{l,pos-1,p}+f_{pos+1,r,p}) \]其中 \(cnt_{pos,p}\) 表示行驶区间在 \([l,r]\) 内且跨越 \(pos\) 位置又能接受 \(p\) 价格的人的数量。
这个方程式显然不完整,因为它只包含了这个区间有定价为 \(p\) 的点的情况。如果整个区间都是 \(>p\) 的定价,那么我们完全可以从 \(f_{l,r,p+1}\) 转移过来。这样的转移就完整了。
最后一个问题就是如何计算 \(cnt_{pos,p}\)。我们在枚举 \(l,r,pos\) 的时候我们可以枚举每一个人计算,不难发现每个人都是接受一个价格前缀的,所以我们可以差分。这样我们可以在 \(O(m)\) 解决这个问题。
输出方案的话同样记录 \(f_{l,r,p}\) 是从哪个位置还是从 \(f_{l,r,p+1}\) 转移过来,最后 DFS 一遍即可。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int cval[4005],ccnt;
int l[4005],r[4005],c[4005];
int f[55][55][4005],ans[55],o[55][55][4005];
int tmp[4005];
const int SIG=1e8;
void getans(int l,int r,int val){
if(l>r)return;
if(o[l][r][val]==0){
for(int i=l;i<=r;i++)ans[i]=cval[val];
return;
}
else if(o[l][r][val]==SIG)getans(l,r,val+1);
else{
ans[o[l][r][val]]=cval[val];
getans(l,o[l][r][val]-1,val);
getans(o[l][r][val]+1,r,val);
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++)cin>>l[i]>>r[i]>>c[i],cval[++ccnt]=c[i];
sort(cval+1,cval+ccnt+1);
ccnt=unique(cval+1,cval+ccnt+1)-cval-1;
for(int i=1;i<=m;i++){
c[i]=lower_bound(cval+1,cval+ccnt+1,c[i])-cval;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int k=j;k<=j+i-1;k++){
memset(tmp,0,sizeof tmp);
for(int p=1;p<=m;p++)if(l[p]>=j&&l[p]<=k&&r[p]>=k&&r[p]<=j+i-1)tmp[c[p]]++;
for(int p=ccnt;p>=1;p--)tmp[p]+=tmp[p+1];
for(int p=1;p<=ccnt;p++){
if(f[j][j+i-1][p]<tmp[p]*cval[p]+f[j][k-1][p]+f[k+1][j+i-1][p]){
f[j][j+i-1][p]=tmp[p]*cval[p]+f[j][k-1][p]+f[k+1][j+i-1][p];
o[j][j+i-1][p]=k;
}
}
}
for(int p=ccnt;p>=1;p--){
if(f[j][j+i-1][p]<f[j][j+i-1][p+1]){
f[j][j+i-1][p]=f[j][j+i-1][p+1];
o[j][j+i-1][p]=SIG;
}
}
}
}
cout<<f[1][n][1]<<"\n";
getans(1,n,1);
for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
return 0;
}
背包 DP
P1941 [NOIP2014 提高组] 飞扬的小鸟
题意
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为 \(n\),高为 \(m\) 的二维平面,其中有 \(k\) 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 \(1\),竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 \(x\),每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 \(y\)。小鸟位于横坐标方向不同位置时,上升的高度 \(x\) 和下降的高度 \(y\) 可能互不相同。
小鸟高度等于 \(0\) 或者小鸟碰到管道时,游戏失败。小鸟高度为 \(m\) 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
\(n\leq 10000,m\leq 1000\)。
解法
直接从左到右扫一遍,如果遇到管道那就设置强制不可达。
特判下降和最高点的转移,中间的转移枚举同余系然后扫一遍中间的数就行了。背包的转移是简单的。
不是依赖性背包。
代码
#include<bits/stdc++.h>
using namespace std;
int dp[2][1005];
int n,m,k;
int upo[10005],downo[10005];
int pos[10005],L[10005],R[10005];
int id[10005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>k;
for(int i=1;i<=n;i++)cin>>upo[i]>>downo[i];
for(int i=1;i<=k;i++)cin>>pos[i]>>L[i]>>R[i],id[pos[i]]=i;
int now=1,ed=0;
dp[ed][0]=1e9;
int cnt=0;
for(int i=1;i<=n;i++){
memset(dp[now],0x3f,sizeof dp[now]);
for(int j=1;j<m;j++)dp[now][m]=min(dp[now][m],dp[ed][j]+(m-j+(upo[i]-1))/upo[i]);
dp[now][m]=min(dp[now][m],dp[ed][m]+1);
for(int j=m-downo[i];j>=1;j--)dp[now][j]=min(dp[now][j],dp[ed][j+downo[i]]);
for(int j=1;j<=upo[i];j++){
int tmp=1e9;
for(int k=j;k<m;k+=upo[i]){
dp[now][k]=min(dp[now][k],tmp+1);
tmp=min(tmp+1,dp[ed][k]);
}
}
if(id[i]){
for(int j=1;j<=L[id[i]];j++)dp[now][j]=1e9;
for(int j=R[id[i]];j<=m;j++)dp[now][j]=1e9;
cnt++;
}
bool flag=0;
for(int j=1;j<=m;j++)if(dp[now][j]<1e8)flag=1;
if(!flag)return cout<<0<<"\n"<<cnt-1,0;
swap(now,ed);
}
int ans=1e9;
for(int i=1;i<=m;i++){
ans=min(dp[ed][i],ans);
}
cout<<1<<"\n"<<ans;
return 0;
}