朗之万动力学原理简介
本文的主要内容是基于以下教程:Tutorial on Diffusion Models for Imaging and Vision
此教程写的非常好,非常推荐大家学习。教程的语言风格也很亲切,时不时地蹦出诸如“这是地球人能想出来的公式?”这样的话,为你枯燥的学习过程增添些许趣味。
朗之万动力学(Langevin Dynamics)是扩散模型和score matching方法中的采样过程,是文本生成图像中的一个重要步骤。想要洞悉文生图的基本原理,朗之万动力学是绕不开的话题。
给定一个已知的概率分布 \(p(\mathbf{x})\),我们的目标是采样出概率密度更大的哪些样本。解决这个问题有多种方法,比如生成伪随机均匀分布,然后用概率分布变换的方法;或者用马尔可夫链蒙特卡洛方法(MCMC)。而朗之万动力学给出的方法是这样:
随机选取空间中一个点(这是很简单的,采用高斯生成与 \(\mathbf{x}\) 同维度的样本就可以),然后计算概率密度函数在该点的梯度,然后沿着梯度的方向计算下一个点,直到收敛。为了防止收敛到局部极大值,我们在每一步迭代计算的时候都会增加高斯噪声。下面我们给出定义和公式:
朗之万动力学,是从已知的概率分布 \(p(\mathbf{x})\) 中进行迭代采样 \(t=1, \ldots, T\) :
\[\begin{aligned} \mathbf{x}_{t+1}=\mathbf{x}_t+\tau \nabla_{\mathbf{x}} \log p\left(\mathbf{x}_t\right)+\sqrt{2 \tau} \mathbf{z}, \quad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I}) \quad\quad\quad\quad (1) \end{aligned} \\ \]其中 \(\tau\) 是设定好的迭代步长,用于控制迭代过程,类似SGD中的学习率。初始值 \(\mathbf{x}_0\) 是白噪声。聪明的读者已经意识到了,这像极了随机梯度下降法(SGD)。没错!朗之万动力学就可以理解为梯度下降法!只不过,朗之万动力学是求概率密度极大值。
朗之万动力学就是随机梯度下降!
我们给出一个可视化结果。假设数据分布为高斯混合分布,是两个高斯分布混合的情况,那么,如果每一步不添加噪声,朗之万动力学的迭代过程是这个样子的:
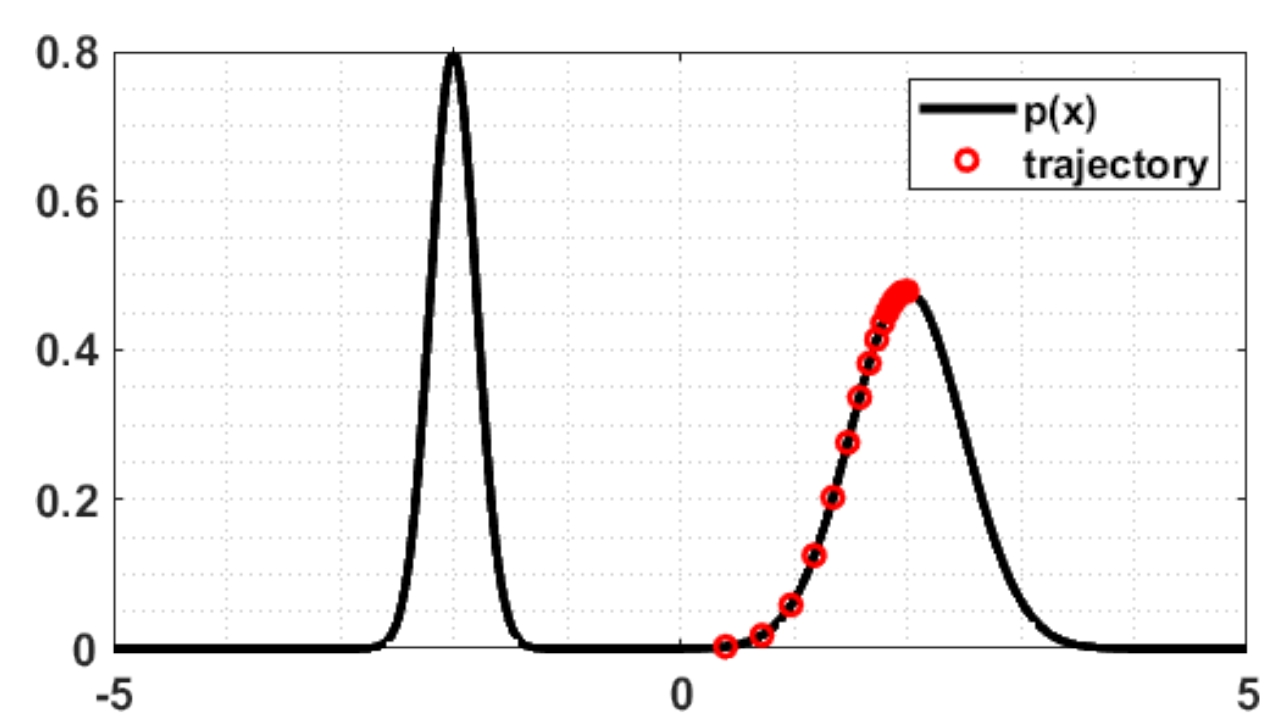
可以看到,收敛到局部极大值点就不再变了。如果每一步添加噪声,那么迭代过程是这个样子的:

这时候接近局部极大值点的时候,是逐步震荡收敛的。
下面我们给出公式(1)是怎么来的,它和物理学中的朗之万动力学又有什么关系。大家不要被朗之万动力学这个名词吓到,其实,阅读此文不需要有大学物理背景,只需要有高中物理知识,同时会一点点微积分就可以了。
一、预备知识
1、牛顿第二定律
力 \(\mathbf{F}\) 等于质量 \(m\) 和 加速度 \(\mathbf{a}(t)\) 的乘积。
\[\begin{aligned} \mathbf{F} = m \mathbf{a}(t) = m \frac{d\mathbf{v}(t)}{dt} \end{aligned} \\ \]其中加速度 \(\mathbf{a}(t)\) 和 速度 \(\mathbf{v}(t)\) 是时间的函数。\(\mathbf{a}(t)\) 是 \(\mathbf{v}(t)\) 对时间的导数。好,很简单,没什么问题。唯一需要注意的是,我们这里的矢量(vector)用 粗体 表示,标量(scalar)用 细斜体 表示。下面也一样。
2、力与能量的关系
这个可能部分读者不太熟悉。我们从动能定理开始。动能定理(kinetic energy theorem)描述的是物体动能的变化量与合外力所做的功的关系,具体内容为:合外力对物体所做的功,等于物体动能的变化量。公式如下:
\[\begin{aligned} \langle\mathbf{F}, \mathbf{s}\rangle = E_2 - E_1 = \frac{1}{2}m||\mathbf{v}_2||^2 - \frac{1}{2}m||\mathbf{v}_1||^2 \end{aligned} \\ \]这里\(\mathbf{s}\)指的是位移,也就是位置的变化。\(\langle\cdot, \cdot\rangle\) 表示矢量内积。\(E\) 代表物体的动能。我们用\(\mathbf{x}\)表示位置,那么位移就等于位置的变化 \(\mathbf{s} = \Delta \mathbf{x}\)。于是我们重写上式:
\[\begin{aligned} \langle\mathbf{F}(\mathbf{x}), \Delta \mathbf{x}\rangle = \Delta E(\mathbf{x}) \end{aligned} \\ \]力和能量是随着物体的位置而变化的,因此是位置 \(x\) 的函数。进一步,我们可以微元化:
\[\begin{aligned} \langle\mathbf{F}(\mathbf{x}), d \mathbf{x}\rangle &= d E(\mathbf{x}) \\ \mathbf{F}(\mathbf{x}) &= \nabla_{\mathbf{x}} E(\mathbf{x}) \end{aligned} \\ \]因此,力是动能对于位移方向的梯度。另外,我们将系统内粒子的能量分为动能和势能,除了动能之外的所有能量都为势能,我们用\(\mathbf{U}(\mathbf{x})\)来表示势能。总能量为\(E_w\),根据能量守恒定律:\(E_w = U(\mathbf{x}) + E(\mathbf{x})\),因此:
\[\begin{aligned} \mathbf{F}(\mathbf{x}) &= \nabla_{\mathbf{x}} E(\mathbf{x}) \\ &= \nabla_{\mathbf{x}} (E_w - U(\mathbf{x})) \\ &= - \nabla_{\mathbf{x}} U(\mathbf{x}) \\ \end{aligned} \\ \]我们得出结论,力是粒子势能的负梯度。
3、玻尔兹曼分布
在热力学与统计物理中。每个粒子的分布的位置是一个随机变量,粒子的分布一般用玻尔兹曼分布来表示:
\[\begin{aligned} p(\mathbf{x}) &= \frac{1}{Z} \exp\left\{-U(\mathbf{x})\right\} \\ \end{aligned} \\ \]其中 \(Z\) 是归一化系数。我们可以直观地理解,对于势能特别大的地方,粒子出现的概率很小;势能特别小的地方,说明粒子的动能比较大,运动比较剧烈,分布比较密集。这是符合我们的人类感知的,你看一般人口比较密集的地方都比较喧闹,如商场和闹市区;人口稀疏的地方,比较安静。
二、推导朗之万动力学
一百多年前,著名物理学家朗之万给出了布朗运动方程:
\[\begin{aligned} m \frac{d\mathbf{v}(t)}{dt} &= -\gamma \mathbf{v}(t) + \bm{\eta} \quad\quad\quad \bm{\eta} \sim \mathcal{N}(\mathbf{0}, \sigma^2 \mathbf{I}) \quad\quad\quad (2)\\ \end{aligned} \\ \]我们不必纠结这个方程怎么来的。我们其实可以很轻松地读懂这个方程。这本质上就是牛顿第二定律的拓展,等式左边就是质量和加速度的乘积,等式右边是力。其中 \(-\gamma \mathbf{v}(t)\) 是和速度有关的摩擦力,它和物体的运动方向相反,所以加个负号,\(\gamma\) 是动摩擦因数。\(\bm{\eta}\) 是随机力,服从均值为 \(0\),协方差矩阵为 \(\sigma^2 \mathbf{I}\) 的高斯分布。
由牛顿第二定律和力与能量的关系可知:
\[\begin{aligned} m \frac{d\mathbf{v}(t)}{dt} &= -\nabla_{\mathbf{x}} U(\mathbf{x}) \\ \end{aligned} \\ \]代入(2)式,于是有:
\[\begin{aligned} -\nabla_{\mathbf{x}} U(\mathbf{x}) &= -\gamma \mathbf{v}(t) + \bm{\eta} \\ \mathbf{v}(t) &= \frac{1}{\gamma}\nabla_{\mathbf{x}} U(\mathbf{x}) + \frac{1}{\gamma}\bm{\eta} \\ \end{aligned} \\ \]速度是位移随时间的导数,另外,将随机力简化为标准高斯分布\(\bm{\eta} = \sigma \mathbf{z}\),有:
\[\begin{aligned} \frac{d\mathbf{x}(t)}{dt} &= \frac{1}{\gamma}\nabla_{\mathbf{x}} U(\mathbf{x}) + \frac{\sigma}{\gamma}\mathbf{z} \quad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I})\\ \end{aligned} \\ \]时间离散化:
\[\begin{aligned} \frac{\mathbf{x}_{t+1} - \mathbf{x}_{t}}{\Delta t} &= \frac{1}{\gamma}\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) + \frac{\sigma}{\gamma}\mathbf{z} \\ \mathbf{x}_{t+1} - \mathbf{x}_{t} &= \frac{\Delta t}{\gamma}\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) + \frac{\sigma \Delta t}{\gamma}\mathbf{z} \\ \end{aligned} \\ \]这里 \(\Delta t\) 是离散采样时间间隔,是常数,\(\gamma\) 是动摩擦因数,也是常数。我们用常数 \(\tau = \frac{\Delta t}{\gamma}\),于是有:
\[\begin{aligned} \mathbf{x}_{t+1} - \mathbf{x}_{t} &= \tau\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) + \tau \sigma \mathbf{z} \\ \mathbf{x}_{t+1} &= \mathbf{x}_{t} + \tau\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) + \tau \sigma \mathbf{z} \\ \end{aligned} \\ \]到这里我们稍微停一下。根据(2)式所描述的过程,最终粒子会越来越集中,还是越来越分散?对(2)式两边取期望,可以发现,粒子的速度是越来越小的,即动能是越来越小的,粒子往势能增大的方向扩散。根据玻尔兹曼分布,粒子的概率密度会越来越小。而我们希望的是相反的方向,即采样出概率密度最大的样本。因此需要对上式右边梯度的符号进行修改:
\[\begin{aligned} \mathbf{x}_{t+1} &= \mathbf{x}_{t} - \tau\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) + \tau \sigma \mathbf{z} \quad\quad\quad (3)\\ \end{aligned} \\ \]根据玻尔兹曼分布:
\[\begin{aligned} \nabla_{\mathbf{x}} \log p(\mathbf{x}_{t}) &= \nabla_{\mathbf{x}} \left\{ \log \frac{1}{Z} - U(\mathbf{x}_{t})\right\} \\ \\ &= -\nabla_{\mathbf{x}} U(\mathbf{x}_{t}) \end{aligned} \\ \]代入(3)式,有:
\[\begin{aligned} \mathbf{x}_{t+1} &= \mathbf{x}_{t} + \tau \nabla_{\mathbf{x}} \log p(\mathbf{x}_{t}) + \tau \sigma \mathbf{z} \quad\quad\quad (4)\\ \end{aligned} \\ \]对比 (1) 式和 (4) 式,是不是感觉几乎一样了呢?\(\tau\) 是常数,方差\(\sigma\)也是常数。我们深度学习计算中的常数值几乎都可以替换或者舍弃,或者可以人工指定。令\(\sigma = \sqrt{2/\tau}\),我们就得到了 (1) 式:
\[\begin{aligned} \mathbf{x}_{t+1}=\mathbf{x}_t+\tau \nabla_{\mathbf{x}} \log p\left(\mathbf{x}_t\right)+\sqrt{2 \tau} \mathbf{z}, \quad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I}) \end{aligned} \\ \] 标签:mathbf,nabla,动力学,end,quad,frac,aligned From: https://www.cnblogs.com/txdt/p/18217435