[NOIP2015 提高组] 运输计划

题目背景

NOIP2015 Day2T3

题目描述

公元 \(2044\) 年，人类进入了宇宙纪元。

L 国有 \(n\) 个星球，还有 \(n-1\) 条双向航道，每条航道建立在两个星球之间，这 \(n-1\) 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 \(u_i\) 号星球沿最快的宇航路径飞行到 \(v_i\) 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 \(j\)，任意飞船驶过它所花费的时间为 \(t_j\)，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 \(m\) 个运输计划。在虫洞建设完成后，这 \(m\) 个运输计划会同时开始，所有飞船一起出发。当这 \(m\) 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入格式

第一行包括两个正整数 \(n, m\)，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 \(1\) 到 \(n\) 编号。

接下来 \(n-1\) 行描述航道的建设情况，其中第 \(i\) 行包含三个整数 \(a_i, b_i\) 和 \(t_i\)，表示第 \(i\) 条双向航道修建在 \(a_i\) 与 \(b_i\) 两个星球之间，任意飞船驶过它所花费的时间为 \(t_i\)。

数据保证

接下来 \(m\) 行描述运输计划的情况，其中第 \(j\) 行包含两个正整数 \(u_j\) 和 \(v_j\)，表示第 \(j\) 个运输计划是从 \(u_j\) 号星球飞往 \(v_j\)号星球。

输出格式

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

样例 #1

样例输入 #1

样例输出 #1

提示

所有测试数据的范围和特点如下表所示

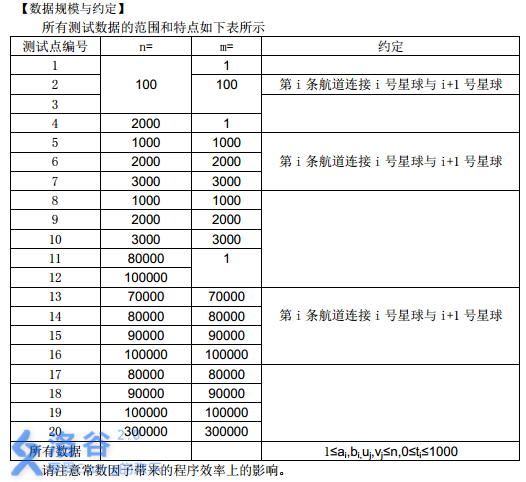
请注意常数因子带来的程序效率上的影响。

对于 \(100\%\) 的数据，保证：\(1 \leq a_i,b_i \leq n\)，\(0 \leq t_i \leq 1000\)，\(1 \leq u_i,v_i \leq n\)。

这题可以用LCA或树链剖分
方法很多

23_9G写法

每次描述运输计划的情况时，算出x->y的总时间,然后记录路径,把路径外的max只更新一下(如图下)

然后统计出那一条路径权值最大,一定是改这条路径上的一条边
最后依次遍历（从下往上一个一个点走）比较res=min(res,max(sum-a[x],quemx(1,dfn[x])))这个意思是比较当前这个点所在的路径上次大边所用的最大时间和最大边减去相应边权,最终要取最小的答案

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5;
int n,m,xx,yy,sum,a[N];
int head[N],tot;
struct E{int u,v,w;} e[N<<1];
inline void add(int u,int v,int w){e[++tot]={head[u],v,w}; head[u]=tot;}

int son[N],dep[N],fa[N],sz[N],top[N],dfn[N],cnt,rk[N];
void dfs1(int u,int f)
{
	sz[u]=1; son[u]=-1; fa[u]=f; dep[u]=dep[f]+1;
	for(int i=head[u];i;i=e[i].u)
	{
		int v=e[i].v;
		if(v==f) continue;
		a[v]=e[i].w;
		dfs1(v,u);
		sz[u]+=sz[v];
		if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
	}
}
void dfs2(int u,int t)
{
	top[u]=t; dfn[u]=++cnt; rk[cnt]=u;
	if(son[u]==-1) return;
	dfs2(son[u],t);
	for(int i=head[u];i;i=e[i].u)
	{
		int v=e[i].v;
		if(v^fa[u]&&v^son[u]) dfs2(v,v);
	}
}
struct T
{
	int l,r,sum,mx,lz;
	#define l(x) tr[x].l
	#define r(x) tr[x].r
	#define sum(x) tr[x].sum
	#define mx(x) tr[x].mx
	#define lz(x) tr[x].lz
	#define ls(x) (x << 1)
	#define rs(x) (x << 1 | 1)
} tr[N<<2];
void down(int k)
{
	if(lz(k))
	{
		mx(ls(k))=max(mx(ls(k)),lz(k));
		mx(rs(k))=max(mx(rs(k)),lz(k));
		lz(ls(k))=max(lz(ls(k)),lz(k));
		lz(rs(k))=max(lz(rs(k)),lz(k));	
		lz(k)=0;	
	}
}
void update(int k,int l,int r,int v)
{
	if(l(k)>=l&&r(k)<=r) {mx(k)=max(mx(k),v); lz(k)=max(lz(k),v); return;}
	down(k);
	int mid=l(k)+r(k)>>1;
	if(l<=mid) update(ls(k),l,r,v);
	if(r>mid) update(rs(k),l,r,v);
	mx(k)=max(mx(ls(k)),mx(rs(k)));
}
int quemx(int k,int p)
{
	if(l(k)==r(k)) return mx(k);
	down(k);
	int mid=l(k)+r(k)>>1;
	if(p<=mid) return quemx(ls(k),p);
	else return quemx(rs(k),p);
}

void bui(int k,int l,int r)
{
	l(k)=l; r(k)=r;
	if(l==r) {sum(k)=a[rk[l]]; return;}
	int mid=l+r>>1;
	bui(ls(k),l,mid); bui(rs(k),mid+1,r);
	sum(k)=sum(ls(k))+sum(rs(k));
}
int quesum(int k,int l,int r)
{
	if(l<=l(k)&&r>=r(k)) return sum(k);
	int mid=l(k)+r(k)>>1,res=0;
	if(l<=mid) res+=quesum(ls(k),l,r);
	if(r>mid) res+=quesum(rs(k),l,r);
	return res;
}

int quepath(int x,int y)
{
	int res=0;
	while(top[x]^top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		res+=quesum(1,dfn[top[x]],dfn[x]);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	res+=quesum(1,dfn[x]+1,dfn[y]);
	return res;
}

#define fi first
#define se second
pair<int,int> q[N];
void mdfmx(int x,int y,int now)
{
	q[0].fi=0;
	while(top[x]^top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		q[++q[0].fi]=make_pair(dfn[top[x]],dfn[x]);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	q[++q[0].fi]=make_pair(dfn[x]+1,dfn[y]);
	sort(q+1,q+1+q[0].fi);
	if(q[1].fi>1) update(1,1,q[1].fi-1,now);
	if(q[q[0].fi].se<n) update(1,q[q[0].fi].se+1,n,now);
	for(int i=1;i<q[0].fi;i++) update(1,q[i].se+1,q[i+1].fi-1,now);


}
int find(int x,int y)
{
	int res=2147483647;
	if(x==y) return 0;
	if(dep[x]<dep[y]) swap(x,y);
	while(dep[x]!=dep[y]) res=min(res,max(sum-a[x],quemx(1,dfn[x]))),x=fa[x];
	while(x!=y)
	{
		if(dep[x]<dep[y]) swap(x,y);
		res=min(res,max(sum-a[x],quemx(1,dfn[x])));x=fa[x];
	}
	return res;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
	{
		int x,y,z; scanf("%d%d%d",&x,&y,&z);
		add(x,y,z); add(y,x,z);
	}
	dfs1(1,0); dfs2(1,1); bui(1,1,n);
	for(int i=1;i<=m;i++)
	{
		int x,y; scanf("%d%d",&x,&y);
		int tmp=quepath(x,y);
		mdfmx(x,y,tmp);
		if(tmp>=sum) xx=x,yy=y,sum=tmp;
	}
	printf("%d\n",find(xx,yy));
	return 0;
}

23_wlesq做法