CF1085D Minimum Diameter Tree 题解

比较水的一道绿题

观察样例可以发现，边权都平分在叶子节点唯一的一条连边上，由此猜到联想到可以把贪心地将边权全部平均分配到这些边上，这样写出来就能AC了。

如何证明

先来一张图方便理解：

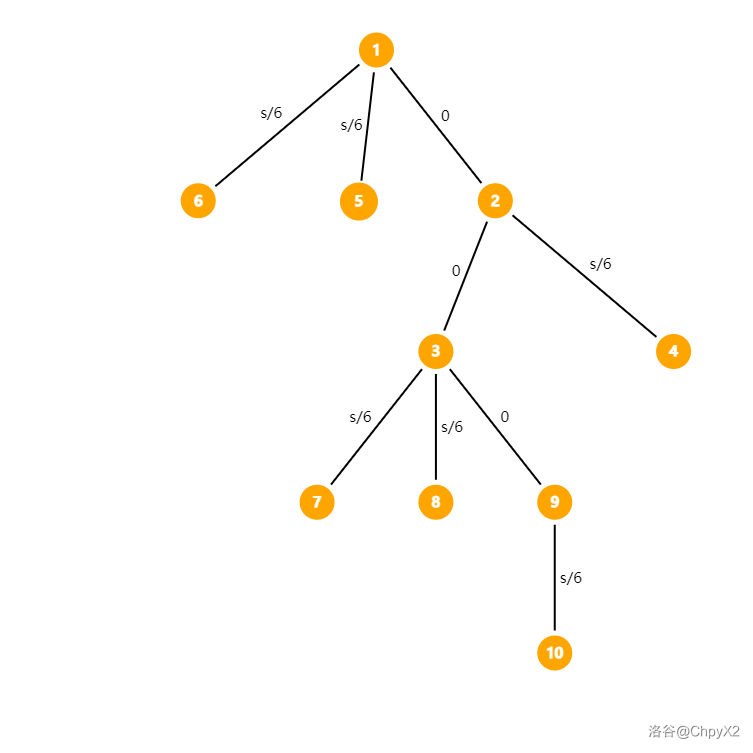
利用反证法：假设按上述做法分配边权后可以至少修改一次并得到更好选择。

那么一定会需要把至少一条在叶子节点上的边的边权减小，并且增加另一条边的边权。

分情况讨论增加边权的那一条边：

• 若这条边也连接叶子节点，显而易见的，从这出发，一定能找到另外一个连边未减小的叶子节点，那么此时这条边是直径，且长度会增加

• 若这条边不连接叶子节点，更加显而易见的，一定有一条边穿过连边边权未减小的两个叶子节点，那么此时这条边是直径，且长度也会增加

• 特殊考虑一下只有一条边的情况，显而易见满足之前所述规律

所以显而易见的,把边权平均分配到叶子边上就行。

细节：

• 要求误差在 \(10^{-6}\) 以内,所以要记得在printf内设置一下

Code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int d[maxn],u,v,n;
double s,c;
int main(){
    cin>>n>>s;
    for(int i=1;i<n;i++){
        cin>>u>>v;
        d[u]++;
        d[v]++;//计算度数
    }
    for(int i=1;i<=n;i++)if(d[i]==1)c++;//度数为1的就是叶子节点,相应的有一条叶子边
    printf("%.10f",s/c*2);
    return 0;
}

Written by ChpyX2