树链剖分

树链剖分 在 DFS 树上把连续的一段有祖先关系的单独开一个序列存储。

查询每一个位置, 不断地往链头条, 然后跳到链头的父亲的链上 \(\dots\)

如果按 DFS 徐直接搞, 会被以下数据 hack

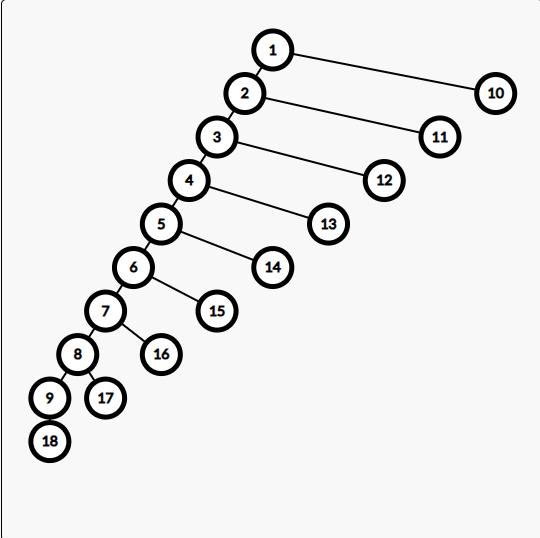
可行的序列有 \(:[1 10], [2, 10], [3, 12], [4, 13], [5, 14], [6, 15], [7, 16], [8, 17], [9, 18]\), 如果查询从 \(18 \to 1\), 单次时间复杂度 \(O(N)\)

重链优化

对于一个节点, 选他儿子子树最大的儿子最当前节点链的后续。

这样, 考虑一个节点往根跳, 每一次, 为了不会父亲在一个重链上, 至少有一个兄弟的节点数量 \(\ge\) 当前的数量, 所以为了让这个节点到根经过 \(k\) 个重链, 整个树至少要有 \(2^k\) 个节点。所以如果有 \(n\) 个点, 单次查询最坏是 \(O(\log_2 n)\)。

这样子的序列也满足 DFS 序的性质

伪代码

void dfs1(int u){
  sz[u] = 1;
  for(auto v : g[u]){
    dfs1(v);
    sz[u] += sz[v];
    if(sz[son[u]] < sz[v]){
      son[u] = v;
    }
  }
}

void dfs2(int x){
  dfn[x] = ++cnt;
  if(son[x]){
    top[son[x]] = top[x];
    dfs2(son[x]);
  }
  for(auto v : g[x]){
    if(v != son[x]){
      top[v] = v;
      dfs2(v);
    }
  }
}