2024.4.3
\(40+100+40=180\)。今天过了一题/开心
草了,T2 空间开大 MLE 了,实际上只过了 \(0\) 题,如果不算这个就登顶了
fibonacci
首先答案一定可以在 \(S_{31}\) 中找到。具体地,找到最大的 \(i\) 使得 \(S_{i-4}< 3|t|\),取 \(S_i\) 即可。
这是因为首先任意三个相邻位置都至少有一个 a 一个 b,因为这个过程可以看做 \(a\to ab,b\to a\),或者归纳也可以证明。那么答案串 \(ans\) 满足 \(|ans|\le 3|t|\)。然后如果 \(S_{i-4}\ge 3|t|\),那么
如果答案可以在 \(S_i\) 中找到,要么 \(ans\in S_{i-2}\),或者 \(ans\in S_{i-1}\),或者 \(ans\) 跨过了 \(S_{i-1},S_{i-2}\) 中间的分割线。然后由于 \(S_{i-4}\ge 3|t|\ge |ans|\),因此 \(ans\) 不可能跨过 \(+\) 左右两侧的 \(S_{i-3}\) 或 \(S_{i-4}\),由于 \(S_{i-3}S_{i-4}=S_{i-2}\),因此 \(ans\) 仍然被包含在 \(S_{i-2}\) 中。于是 \(S_i\) 就没有用了。
具体地,有 \(|S_{28}|=514229\ge 450000\),于是我们取到 \(S_{31}\) 即可。看上去取 \(S_{30}\) 也能过
设 \(to_{i,j}\) 表示 \(S_i\) 这个串,从 \(t_j\) 开始走,会走到哪个 \(t_k\)。\(to\) 可以递推得出。
考虑双指针,考虑如何 check 一个区间能否走完 \(t\)。建一个类似 segtree 的结构,把区间拆成 \(O(\log t)\) 个完整的 \(S_j\),利用 \(to\) 判断即可。
复杂度 \(O(|t|\log |t|)\)。常数大概有很多倍。跑的贼慢,喜提最劣解。
tap
这不是我们 PA2024 kra 吗后面忘了
后面是:
只需要求能到达每个区间的区间个数。
对每个区间 \([l,r]\),找到 \(l\) 上面的第一个区间和 \(r\) 上面的第一个区间,然后分别连边,得到两棵树。
那么我们会从 \([l,r]\) 一路向上扩展,直到被完全覆盖。找到这个完全覆盖的,那么合法区间就是覆盖过程中经过的若干段阴影区域拼起来。倍增求一下链上和就好了。
这里还需要求第一个被覆盖到的区间,发现这就是支配树上它的父亲,只需要求 DAG 的支配树。这个很好求:任取拓扑序,对每个 \(u\),其入边分别为 \(v_1,v_2,\cdots,v_k\),找到 \(\text{LCA}(v_1,v_2,\cdots,v_k)\),则 \(u\) 的支配点就是这个 LCA。连边接着递推即可。
跑得贼快,喜提最优解。
哦,这个题还有一个前面:他是每次随机一个未选中的,然后选中它。这个等价于随机排列,每次如果已经被覆盖了就跳过。也等价于每次在 \(n\) 个里面随机,如果遇到了覆盖过的就跳过。
polygon
首先介绍处理实数随机的一些方法:把每个数拆成整数部分和小数部分,看成 \(x_i=y_i+z_i\),其中 \(y_i\) 是 \([0,2^{a_i}-1]\) 中的一个随机整数,\(z_i\) 是 \([0,1)\) 中随机的一个实数。
考虑怎么算 \(n\) 个 \([0,1]\) 中的随机实数加起来 \(\le k\) 的概率,嗯这个当然可以类似我场上写的 6KB 维护分段多项式,\(O(n^2)\) 算出来。说不定强大的 poly 也可以把这个优化到 soft O(n)
考虑写一下这个式子,他就是
\[\int_{0}^{\infty}\int_{0}^{\infty}\cdots\int_{0}^{\infty}\left[\sum x_i\le k\right][x_1\le 1][x_2\le 1]\cdots[x_n\le 1]\ \text{d}x_1\text{d}x_2\cdots\text{d}x_n \]然后他等于
\[\int_{0}^{\infty}\int_{0}^{\infty}\cdots\int_{0}^{\infty}\left[\sum x_i\le k\right](1-[x_1\ge 1])(1-[x_2\ge 1])\cdots(1-[x_n\ge 1])\ \text{d}x_1\text{d}x_2\cdots\text{d}x_n \]额当然由于是实数所以取等啥的都无所谓。然后再拆开,需要算一些
\[\binom{n}{j}(-1)^j\int_{0}^{\infty}\int_{0}^{\infty}\cdots\int_{0}^{\infty}\left[\sum x_i\le k-j\right][x_1\ge 0][x_2\ge 0]\cdots[x_n\ge 0]\ \text{d}x_1\text{d}x_2\cdots\text{d}x_n \]然后这个你每次积分,就得到,他其实是 \(\frac{(k-j)^n}{n!}\)。然后一遍卷积就可以 \(O(n\log n)\) 算出 \(P_k=\mathbb{Pr}\left[\sum z_i\le k\right]\)。
接下来考虑整数部分。数位 DP,初值设为 \(dp(0,j)=P_{j+1}-P_j\),就表示我在第 \(0\) 位上放 \(j\) 个 \(1\)。剩下的我们都很熟悉。(NOIP2021 T2 / QOJ8009)卷积优化一下即可。复杂度 \(O(an\log n)\)。
其实代码我不太想写......已加入《实在没事干了.md》
ICPC Nanjing 2023 D
\(f(u,j)\) 表示 \(u\) 子树内,每个点到叶子都有 \(j\) 个黑点的最小代价。
那么每次是把儿子的 \(f\) 直接相加,然后和 \(x_{u,0/1}\) 做 min+ 卷积,其中 \(x_{u,c}\) 表示将 \(u\) 点改成颜色 \(c\) 的最小代价。
显然 \(x\) 也凸,那么 \(f\) 自然就是凸的。
slope trick 随便做做,这里合并的时候可以用长剖合并,复杂度是 \(O(n\log n)\)。
然后也存在 \(O(n)\) 做法,大概是利用 \(x_u\) 的斜率是 \(1\) 或 \(-1\),分别维护正负两边的两个 deque 等等。
ECFinal 2023 C
啊啊怎么是这个题
考虑给每个合法序列 pair \((x_{1\cdots p},y_{1\cdots q})\) 对应唯一的一个加数的顺序,每次如果当前 \(\sum x<\sum y\) 就加一个 \(x\),否则加一个 \(y\)。那么每种方案对应唯一的顺序,且每个顺序中,\(\sum x-\sum y\) 的值永远在 \([-V,V]\) 之间。
于是 \(dp_{i,j,k}\) 表示加入了 \(x_{1\cdots i},y_{1\cdots j}\),目前 \(\sum x-\sum y=k\) 的方案数即可。
每次如果 \(k<0\) 就转移到 \((i+1,j,\cdot)\),否则转移到 \((i,j+1,\cdot)\)。转移用前缀和优化,复杂度 \(O(n^2V)\)。
subset sum in O(nW)
是这样,给 \(n\) 个 \([0,W]\) 中的数 \(x_1,\cdots,x_n\),然后给 \(T\in[0,nW]\),问能否选一个子集 \(S\) 使得 \(\sum_{i\in S}x_i=T\)。
这个问题还有更强的版本(QOJ7403,max subset sum <= T),然后这两个其实是等价的。
先来解决弱的版本,贪心选取一个子集 \(A\) 使得 \(A\) 任意加入别的元素都会导致子集和 \(>T\),且 \(\sum_{i\in A}x_i\le T\)。这里 \(A\) 可能不唯一,我们任取一个就好。接下来设 \(B=\{x_1,x_2,\cdots,x_n\}-A\),设 \(T'=T-\sum_{i\in A}x_i\),则 \(T'\in[0,W)\)。我们需要选取 \(C\subseteq A,D\subseteq B\),使得 \(\sum_{i\in D}x_i-\sum_{i\in C}x_i=T'\),那么我们就得到一种方案 \(A-C+D\)。
仍然把一种方案唯一对应到一个加入顺序,每次如果当前的和 \(<T'\) 我们就加入一个 \(D\) 中元素,否则加入 \(C\) 中元素。得到 DP:\(f(i,j,k)=0/1\) 表示 \(A\) 的前 \(i\) 个元素,\(B\) 的前 \(j\) 个元素,能否选出 \(\sum_{i\in D}x_i-\sum_{i\in C}x_i=k\) 的子集 \(C,D\),其中 \(k\in[T'-W,T'+W]\)。方便起见设 \(A=\{a_1,a_2,\cdots,a_{|A|}\},B=\{b_1,b_2,\cdots,b_{|B|}\}\),那么转移有:
\[f(i,j,k)\to f(i+1,j,k-a_{i+1}),f(i,j,k)\to f(i+1,j,k)\qquad k\ge T'\\ f(i,j,k)\to f(i,j+1,k+b_{j+1}),f(i,j,k)\to f(i,j+1,k)\qquad k<T' \]这个做法的复杂度仍然为 \(O(n^2W)\)。
注意到有单调性:若 \(f(i,j,k)=\texttt{true}\),则任意的 \(p\ge i,q\ge j\) 均有 \(f(p,q,k)=\texttt{true}\)。考虑设 \(g(i,k)\) 表示最小的 \(j\),使得 \(f(i,j,k)=\texttt{true}\)。
照抄两种转移,发现 \(i\) 的转移比较简单,当 \(k\ge T'\) 时我们直接将 \(g(i,k)\to g(i+1,k),g(i+1,k-a_{i+1})\) 即可;但 \(k<T'\) 的时候我们似乎要枚举 \(j\ge g(i,k)\),然后做转移 \(j+1\to g(i,k+b_{j+1})\)。
额,这好像还是 \(O(n^2W)\)。
注意到 \(g(i,k)\ge g(i+1,k)\),考虑做第三种转移的时候,如果 \(j\ge g(i-1,k)\),那么我们实际上已经转移过 \(j+1\to g(i-1,k+b_{j+1})\to g(i,k+b_{j+1})\) 了,所以只需要枚举 \([g(i,k),g(i-1,k)-1]\) 之间的 \(j\) 去做转移。
这样对于每个 \(k\),枚举的 \(j\) 的总量就是 \(O(n)\) 的,于是总复杂度 \(O(nW)\)。
那么 max subset sum <= T 怎么做呢。注意到当 \(T\) 不超过所有数之和时,答案和 \(T\) 的差不会超过 \(W\)。于是我们类似地做一遍 DP,然后找到不为 \(\infty\) 的状态来更新答案即可。
https://qoj.ac/submission/376872
CF1810G
看到这个题当然我们就想从前往后 DP,\(dp(i,sum,mx)\) 表示前 \(i\) 个数,和为 \(sum\),前缀最大值为 \(mx\)。但是复杂度是 \(O(n^3)\),也不知道能不能优化。
考虑如果只需要算全局的答案,那么我们可以倒着 DP,\(dp(i,mx)\) 表示 \(i\cdots n\) 这些数,前缀最大值为 \(mx\)。那么往前加一个 \(+1\) 就是 \(mx\leftarrow mx+1\),否则就是 \(mx\leftarrow \max(mx-1,0)\)。
但是我们要算每个前缀的答案,怎么办呢。考虑相当于有一个 \(O(n^2)\) 个节点的图,\((i,j)\) 就表示一个状态 \(dp(i,j)\),然后我们在 \((1,j)\) 这里连一条 \(\times h_j\) 的边到 \((0,0)\),那么就是要算每个点到 \((0,0)\) 的所有路径的边权乘积之和。倒过来 DP 即可。
这个也可以说成,额,转置原理?不太明白呀
这个题 luogu 题解区也有很多精彩做法口牙
ARC168E
那我们肯定想设 \(w(l,r)=\left[\sum_{i=l}^ra_i\ge s\right]\),然后求一下 \(w\) 自己做 max+ 矩乘 \(k\) 次幂的值嘛。但是不管是哪个方向的四边形不等式,\(w\) 都没办法满足。所以这完全不凸,全错了。
\(w\) 不满足四边形不等式的反例:\(s=2,a=(1,1,1)\Rightarrow w(1,2)+w(2,3)>w(1,3)+w(2,2)\);另一方面取 \(s=3,a=(1,1,1)\) 就有 \(w(1,2)+w(2,3)<w(1,3)+w(2,2)\)。
考虑直接钦定最后有 \(x\) 个区间 \([l_1,r_1],[l_2,r_2],\cdots,[l_x,r_x]\),每个区间的和都 \(\ge s\)。那么为了有 \(k\) 段,只需要剩下的数的个数 \(\ge k-x\)。考虑设 \(f(x)\) 表示选 \(x\) 个和 \(\ge s\) 的不交区间,其最小的区间总长是多少。那么 \(f\) 就是凸的了。可以感性理解为随着选取的区间越来越多,\(f\) 增长的也会越来越快,因为会更难选取新的区间。严谨的证明可以在官方题解中找到。
既然是凸的那么就都好办了,我们要找到最大的 \(x\) 使得 \(n-f(x)\ge k-x\),也就是 \(f(x)-x\le n-k\)。显然 \(f(x)-x\) 也是凸的,我们考虑直接二分斜率,找到纵坐标 \(n-k\) 所在的线段,然后就可以 \(O(1)\) 计算出其横坐标。算一个 \(f(x)-kx\) 的切点显然也可以做到 \(O(N)\)。综上,总复杂度 \(O(N\log N)\)。
HDU6566
我草,好像假了,爆了
有人教我一下吗???
2024.4.4
\(100+10+100=210\)。登顶了
A
显然可以 \(O(\log N)\) 算一个前缀 \(i\) 给 \(k\) 个数取反的答案,然后第 \(i\) 行的最优解 \(k_i\) 关于 \(i\) 单调,于是使用你喜欢的决策单调性处理手法即可。复杂度 \(O(N\log^2N)\)。
B
C
首先 \(X=0\) 好做,考虑 \(X\neq 0\),把极长的连续 \(0,X\) 段缩到一起,然后考虑 DP 每次加进来一段,只需要算一段的答案。嗯这个我找规律强行给他爆了,感觉实际推起来比较繁琐。大概是利用前缀 xor 此时只会是 \(0,X\),然后做一些分讨。
然后转移容易优化,做到 \(O(N)\)。
2024.4.5
\(47+71+40=158\),过了 \(0\) 题/开心
T3 就剩一个 case 就写完了,那个 case 写了个乱搞,本来能过 \(2\times 10^5\) 的,结果乱搞阈值开错了直接挂飞了
A
那看到这个就想到容斥嘛,钦定集合 \(S\) 内部为若干个环,偶环造成 \(-1\) 贡献,奇环造成 \(1\) 的贡献,外面的点造成 \(\text{outdeg}\) 的贡献表示随便选出边。然后我场上觉得这没办法优化呀?所以写了枚举 \(S\),枚举排列算这东西的指数及做法。
实际上 \((-1)^{\#\text{even cycles}}=(-1)^{\#\text{inv}}\),所以这就是行列式。为了处理外面的点,给每个点多加 \(\text{outdeg}\) 个自环,这样如果一个点选了新加的自环就表示他没有被钦定在一个我们要求的奇环或者偶环里。
这也就自然是题解说的 \(ans=\text{det}(D+G)\)。
B
看完就猜只需要 \(ab,cd\) 各自不相邻就行,然后很容易得到 \(O(n)\) DP,也容易优化到 \(O(m^3\log n)\)。后面是 poly,跑一下 BM 得到答案的线性递推然后 Bostan-Mori 即可。这里 Bostan-Mori 的多项式乘法可以暴力 \(O(m^2)\) 做,但是我既不会 BM 也不会 Bostan-Mori 哈哈哈
感觉纯烂题,烂完了
C
你就硬分类讨论,\(k=1\) 好做,\(k=2\) 如果不交的话也好做,相交的话一定在笛卡尔树上成祖孙关系,考虑如果选了 \((u,v)\) 其中 \(u\) 是 \(v\) 的祖先,其贡献为 \(-len_v\times h_u+len_u\times h_u+len_v\times h_v\),在祖先处统计,李超树合并维护 \((-len,len\times h)\) 的这些直线即可。
考虑 \(k=3\),三个互相不交的情况 DP 即可,如果可以分成两个不交的部分也好做,然后如果三个形如 \(u,v,w\) 其中 \(u,v,w\) 依次为祖孙关系就只需要把 \(k=2\) 的再做一遍。
唯一难的情况是选一个祖先 \(u\),然后选两个 \(v,w\) 满足 \(v,w\) 互不为祖孙关系,造成的贡献为
\[len_v\times h_v+len_w\times h_w+len_u\times h_u-(len_v+len_w)\times h_u \]我们考虑放宽限制,发现当 \(u\) 不为 \(v,w\) 的祖先时,这个东西不会算的更大。考虑对 \(u\) 不做任何限制,只钦定 \(v,w\) 不交。那么我们需要对一个 \((-len_i,len_i\times h_i)\) 这样的东西求一下凸包,然后和自己做闵可夫斯基和。但还有一个不交的限制,这个该怎么做呢
考虑建一个线段树,每个子树变成一个区间 \([l,r]\),考虑两个不交区间 \([l_1,r_1],[l_2,r_2]\),不妨设 \(r_1<l_2\),我们在 \(\text{LCA}(r_1,l_2)\) 处统计这个贡献。嗯然后大概你就很会了对吧。
具体来说,我们对每个线段树节点维护两个凸包 \(L,R\),然后对每个区间 \([l,r]\),我们在 \(l\) 的所有祖先的 \(L\) 凸包里面插入这个点,\(r\) 的所有祖先的 \(R\) 凸包里面插入这个点,然后我们对每个线段树节点,把他左儿子的 \(R\) 凸包和右儿子的 \(L\) 凸包做闵可夫斯基和,把得到的这些点放到总的点集里面,最后再对总的点集求一遍凸包。求出这个凸包之后,再枚举 \(u\) 计算即可。
综上,总复杂度 \(O(N\log N)\)。
2024.4.6
\(100+100+65=265\),小小登顶了一波
A
\[\sum_{m=0}^n\sum_{k=m}^n\binom{k}{m}\binom{k-m}{\lfloor \frac{k-m}{2}\rfloor}2^{n-k+m}=\sum_{k=0}^{n}2^{n-k}\sum_{m=0}^k\binom{k}{m}2^m\binom{k-m}{\lfloor\frac{k-m}{2}\rfloor} \]后面那一坨就是 \(\binom{2k+1}{k}\)。证明考虑我们有 \(2k+1\) 个数,现在需要选出 \(k\) 个。我们把 \((2i-1,2i)\) 分成一组,这样会分出来 \(k\) 组,和剩下的一个 \(2k+1\)。我们枚举有 \(m\) 组恰好选中了一个元素,方案数是 \(\binom{k}{m}2^m\),表示先选 \(m\) 组,然后在每一组里面决策选哪个。那么根据 \(k-m\) 的奇偶性可以唯一确定 \(2k+1\) 是否被选中,同时剩下的 \(k-m\) 组一定全选了 \(\lfloor \frac{k-m}{2}\rfloor\) 组,于是方案数就只需要再乘一个组合数。
于是容易 \(O(n)\) 预处理 \(O(1)\) 回答询问。
B
容易想到 \(O(n^2)\) DP:\(dp_{i,j}\) 表示目前刚拿出来第 \(i\) 个球,恰好 \(j\) 个球被拿了恰好一次的概率。其中 \(dp_{0,0}=1\),对于 \(i\ge 1\) 我们钦定 \(1\le j\le i\)。转移形如:
\[dp_{i,j}=dp_{i-1,j-1}\times \frac{n-i+1}{n-i+j}+dp_{i,j+1}\times \frac{j+1}{n-i+j+1} \]这个可能没有优化空间,常规的套路是直接维护下降幂 \(f_{i,j}=\sum dp_{i,k}\binom{k}{j}\),那么直接根据组合意义就可以推出 \(f\) 的转移式,这里略过。注意到 \(f\) 的转移只有 \((i,j)\to (i+1,j/j+1)\),而我们用到的只是 \(f_{n,0\cdots,m}\),因此只对这些位置 DP 即可做到 \(O(nm)\)。
C
EZEC 雪的魔法。
首先线性规划对偶,然后转成一个平面图最短路题,类似 PA2021 Desant 2 地做即可。
2024.4.7
eps+eps+eps,具体得分忘了,好像三个题加起来勉强拼上了 \(100\) 出头
又是会 0 题的一天呢/开心
A
转化成二分图匹配之后考虑 Hall 定理,但一个不合法方案可能会有多个集合 \(S\) 满足 \(|N(S)|<|S|\)。考虑对每种不合法方案选取 \(S\) 的代表元,使得代表元唯一,并对代表元计数。这里 \(N(S)\) 表示左部点 \(S\) 在右侧的相邻点集。
我们选取所有 \(|S|>|N(S)|\) 的集合 \(S\) 中 \(|S|-|N(S)|\) 最大的,如果有多个,则选取 \(|S|\) 最小的。那么如果存在两个最优的集合 \(S\neq T\) 使得 \(|S|-|N(S)|=|T|-|N(T)|>0\),则由于 \(|S\cap T|<|S|\),必有 \(|S\cap T|-|N(S\cap T)|<|S|-|N(S)|\)。于是
\[\begin{aligned} |S\cup T|-|N(S\cup T)|&\ge |S|+|T|-|S\cap T|-|N(S)|-|N(T)|+|N(S\cap T)| \\&=|S|-|N(S)|+|T|-|N(T)|-(|S\cap T|-|N(S\cap T)|) \\&>|S|-|N(S)| \end{aligned} \]这就导出了矛盾。第一个不等号是大于等于,是因为 \(|N(S\cap T)|\le |N(S)\cap N(T)|\)(如果一个点被算到了左边,那么显然在右边也会被算进去),而 \(N(S\cup T)=N(S)\cup N(T)\),于是有 \(|N(S\cup T)|+|N(S\cap T)|\le |N(S)\cap N(T)|+|N(S)\cup N(T)|=|N(S)|+|N(T)|\)。
现在考虑计算 \(dp(S,S_1)\) 表示左部点集合 \(S\) 和右部点集合 \(S_1\),只考虑这些点之间的连边,不存在 \(T\subseteq S,T_1\subseteq S_1\) 满足 \((T,T_1)\) 比 \((S,S_1)\) 优的概率。考虑容斥,首先钦定 \(N(S)=S_1\),然后减掉实际的最优不合法子集为 \((T,T_1)\neq (S,S_1)\) 的概率。
考虑这需要什么条件,首先我们钦定恰好有 \(N(T)=T_1\),然后需要 \((S-T,S_1-T_1)\) 合法,否则取 \(C\subseteq S-T,C_1\subseteq S_1-T_1\) 且 \(|C|>|C_1|\) 就有 \((T\cup C,T_1\cup C_1)\) 更优;进一步,由于 \((S-T,S_1-T_1)\) 合法,任取 \(D\subseteq T,C\subseteq S-T\),其 \(D\cup C\) 都不可能比 \(T\) 更优。
综上我们完成了转移,复杂度 \(O(3^{2n})\)。
实际上,考虑加点的过程中动态维护二分图匹配,具体来说我们依次加入左部点,维护每个右部点集合 \(S\) 能否和当前已加入的点形成完美匹配,并动态更新即可。容易发现集合个数不会超过 \(\binom{n}{\lfloor n/2\rfloor}\),于是复杂度有很松的上界 \(2^{\binom{n}{n/2}}\);实现代码后可以发现实际状态数在 \(n\le 7\) 时只有 \(W=40000\) 左右,于是可以在 \(O(n2^nW)\) 的时间复杂度内解决本题。
B
考虑怎么判合法,首先有球的位置肯定得是最靠下的若干个位置,也就是说没有球的位置集合要么为空,要么是包含根的一个连通块。
我们考虑一个点落进来若干个球,如果钦定了他们的顺序,以及他们往哪个儿子里面走,那么其实最终落到哪些点上就是唯一确定的,而且不同的顺序一定也会得到不同的结果。
唉,这个题还是很神秘,我大概会编一个 dp 了,但是这个还是很神秘
题
给 \(m,k,b\),求第 \(m\) 大的,是 \(10^k-1\) 的倍数,且十进制表示下没有数码 \(b\) 的数。
\(m\le 10^{16},k\le 16\)
逐位确定答案,每次计数一下后面的方案数。我们都知道 \(\bmod (x^k-1)\) 就是 \(f_i\to f_{i\bmod k}\) 所以先枚举结果是 \((10^k-1)\times p\) 其中 \(p\) 大概不会超过 \(20\),然后数位 DP,每次把 \(\bmod k\) 相同位的都一起填了,模拟从低到高进位就行。
题题
给 \(m,k,b\),求第 \(m\) 大的 \(x\),满足 \(x\) 十进制下数位没有 \(a\),\((10^k-1)x\) 的十进制表示下没有数码 \(b\)。
\(m\le 10^{16},k\le 16\)
考虑依次填 \(x\),那么 \(10^kx-x\) 可能会有 \(16\) 位要决策是否往后借一位,\(2^{16}\) 枚举之即可。
2024.4.8
\(100+100+100=300\)。?
今天过了 3 题/难过
A
离线后变成若干次查询 \(B[s,t]\) 在 \(A[l,r]\) 中的出现次数,用你喜欢的字符串数据结构维护即可。
例如可以使用 SAM 变成二维数点,容易在 \(O(N\log N)\) 时间内解决。
B
这个问题的研究对象是所有点分树。
先尝试去掉 \(k\) 的限制,计数合法的点分树个数。考虑使用一些合法解来构造更多的合法解,思考怎么把两个子树的点分树合并成一个大的点分树。
设我们现在有 \((u,v)\) 这条边,\(u\) 左边的连通块构成一个点分树,\(v\) 右边的连通块构成一个点分树。
那么要得到两个连通块并起来的点分树,首先我们需要选择全局的根节点,它一定是两边的根节点之一。例如我们选择了 \(u\) 这一侧的点分树根节点作为全局点分树的根节点,那么删去这个根节点后分成若干连通块,不包含 \(u\) 的联通块就没有用了,剩下的部分是 \(u\) 那边的点分树和 \(v\) 那边的点分树接着合并。
于是我们发现实际上我们可以任意归并 \(u\) 到其点分树根节点上的点,和 \(v\) 到其点分树根节点上的点。那么对于没有 \(k\) 的限制的部分,只需要记录这里有多少个点即可。
严格来说,我们还需要证明这个过程的确能得到所有点分树。这部分可以参考 command_block 的博客。
回到本题,注意到 \(k\) 较小,考虑直接暴力把这一条链上的点钦定的标号值 \(p_1,p_2,\cdots,p_x\) 压进状态,注意到它们的顺序一定是从根到 \(u\) 依次递增,且 \(u\) 一定是最后一个,因此只需要存储集合,状态数为 \(O(n2^k)\)。
转移时,假设要合并 \(f(u,S),f(v,T)\),由于最终 \(S,T\) 这些点都会到一条链上,因此他们的标号值一定互不相同;由于我们钦定了标号值,因此归并顺序是唯一的。在归并之后,由于状态的定义是只记录 \(u\) 到根链上的点,因此我们需要把 \(S+T\) 中 \(>\max S\) 中的元素删掉。暴力进行转移,即可得到 \(O(n3^k)\) 的做法。
容易使用子集卷积优化到 \(O(nk^22^k)\),但 \(k\) 只有 \(17\),我感觉其实跑不过 \(n3^k\) 呀......
无语了,std 写的是卡常的 \(O(n3^k)\)
C
相当于维护两个图 \(G,H\),要求支持在 \(G\) 中插入一条边,删除一条边,查询多少个点对 \((i,j)\) 满足 \(i,j\) 在 \(G\) 中连通或者在 \(H\) 中连通。
对每个 \(i\) 维护 \(a_i,b_i\) 表示 \(i\) 在 \(F,G\) 中所在的连通块编号,那么启发式合并维护一下,容易发现只需要维护 \(O(n\log n)\) 次单点修改 \(a,b\),查询多少对 \((i,j)\) 满足 \(a_i=a_j\) 或 \(b_i=b_j\)。简单开个桶维护即可。
我的代码使用了 map,复杂度为 \(O(n\log^2n)\)。
2024.4.9
\(100+100+40=240\)。今天过了 2 题/难过
A
注意到一般情况是 4-SAT,是 NP-Hard 问题,考虑分析约束的性质。
约束形如 \(4\Rightarrow (3\iff 2) \Rightarrow 1\),发现 \(1,4\) 相对而言比较容易确定,而且对约束的影响也不大。考虑贪心地把颜色染为 \(1\) 和 \(4\),然后对剩下的跑二分图染色。
考虑什么时候可以确定一个 \(i\) 一定不能染成 \(4\),把 \(a\) 克制 \(b\) 看做 \(a>b\),不克制看做 \(a\le b\),发现相当于存在 \(x\) 而且能确定 \(x>i\)。那么我们先把那些被直接克制的确定为 \(\neq 4\),然后如果 \(x\neq 4,x\ge y\) 就把 \(y\) 也确定为 \(\neq 4\)。同理也可以确定哪些一定 \(\neq 1\)。然后我们贪心把能填成 \(1,4\) 的都填成 \(1,4\) 即可。
那么剩下的必须是 \(2,3\),跑二分图染色即可。
B
首先 \(p,q\) 都是排列,这意味着我们实际上只需要考察 \(1,2,\cdots,n\) 能变成哪些排列。
其实这个我很熟,之前我还出过一个类似的题......直接猜出来除去 \(m\ge n-1\) 的 corner case,其余情况当 \(2\mid m\) 时可以得到所有逆序对个数不变的排列;\(2\nmid m\) 的时候可以得到所有排列。实现暴力后观察,发现的确如此。
接下来我猜只需要使用 \(len=m+1\) 的操作就够用了,实际上暴力表明确实如此,但是我好像没能构造出来。于是我加上了 \(len=m+2\) 的操作,发现就简单了不少。
先考虑 \(2\nmid m\) 的情形,我们考虑在 \(n\) 次操作内完成一次 swap 相邻两项。考虑我们要交换 \(a,b\),有如下的方法:(其中每次用中括号框起来的是操作的区间)
- \([a,b,x_1,\cdots,x_m] \Rightarrow x_1,\cdots,x_m,a,b\)
- \([x_1,\cdots,x_m,a],b\Rightarrow a,x_1,\cdots,x_m,b\)
接下来我们操作 \(\frac{m-1}{2}\) 次整个区间,每次会把 \(b\) 往前移动两个位置,最后就变成 \(b,a,x_1,\cdots,x_m\)。由于 \(2\nmid m\),因此的确会恰好移动到这个状态。
问题是 \(a,b\) 后面可能不足 \(m\) 个元素。std 的解决方式是,直接任取一个和 \(m\) 互质的长度 \(len\),满足 \(a,b\) 在区间 \([1,len]\) 中,然后不断 shift \([1,len]\) 把 \(a,b\) 换到开头。
我的方法是对最后 \(m+2\) 个元素 shift,直到 \(a,b\) 后面出现了 \(\ge m-1\) 个元素。这种情况根据 \(a,b\) 后面初始元素个数的奇偶性还可能会出现最终得到 \(y,a,b,x_1,\cdots,x_{m-1}\) 的情况。对于这个,我们的方案是:
- \([y,a,b,x_1,\cdots,x_{m-1}]\Rightarrow b,x_1,\cdots,x_{m-1},y,a\)
- \([b,x_1,\cdots,x_{m-1},y],a\Rightarrow x_1,\cdots,x_{m-1},y,b,a\)
然后还是对整个区间往前 shift \(\frac{m-1}{2}\) 次即可。
现在考虑 \(2\mid m\) 的情形。考虑构造出 \(n\) 次操作内 \(a,b,c\to c,a,b\) 的方案,然后依次归位 \(1,2,\cdots,n-2\)(操作 \([i-1,i+1]\) 即可让 \(i\) 向前移动一位,\(i=n\) 就操作 \([i-2,i]\)),由于逆序对个数奇偶性不变,因此 \(n-1,n\) 此时一定已经归位。具体方案是:
- \([a,b,c,x_1,\cdots,x_{m-1}]\Rightarrow c,x_1,\cdots,x_{m-1},a,b\)
- \(c,[x_1,\cdots,x_{m-1},a,b]\Rightarrow c,b,x_1,\cdots,x_{m-1},a\)
- \(c,[b,x_1,\cdots,x_{m-1},a]\Rightarrow c,a,b,x_1,\cdots,x_{m-1}\)
然后同理按照我的处理方法也会遇到 \(y,a,b,c,x_1,\cdots,x_{m-2}\) 的情况,类似上面也可以做。
感觉这题,纯依托,我从九点多做到十二点多,根本没时间做 T3/ng
C
连通块个数为 \(k\) 相当于实际加入了 \(n-k\) 条边。下面令 \(k\leftarrow n-k\)。
显然有 \(O(n^2)\) DP:\(f_{i,j}\) 表示加了 \(i\) 条边,现在还有 \(j\) 个孤立点。
考虑容斥,钦定若干边必须被加入,考虑算此时的方案数。
我们发现这里如果想要去算方案数的话,可能最后需要除掉 \(\binom{n}{2}!\),而这些我们都不太能计算。不过打表发现 \(k=1\) 的方案数是 \(\binom{n}{2}!\times \frac{2^{n-2}}{Cat_n}\),其中 \(Cat_n=\frac{1}{n+1}\binom{2n}{n}\) 为卡特兰数,这表明 \(\binom{n}{2}!\) 大概率会被约掉,我们可以尝试去推一下。
这相当于对这 \(\binom{n}{2}\) 条边的顺序有一些要求,如果一条边的两个端点连接的都是孤立点,那么这条边的顺序我们没有做要求;如果两条边连接的都是被我们钦定的边的端点,那么首先不能成环,它需要在其中靠后加入的那个连通块加入的时刻之前被加入。
那么在确定真的连了哪些边之后,会得到一个森林,我们先尝试对一个森林该怎么算他的概率。首先显然最终的图没有孤立点,于是每个连通块至少有一条边。在确定这个连通块第一条加入的边之后,剩下的概率相当于一棵树的拓扑序。这个对每个子树是独立的,于是可以得到其概率是
\[\prod_{T\in P}\left(\sum_{(u,v)\in T}\prod_{x}\frac{1}{siz_x}\right) \]大概是这样的形式,\(P\) 是所有连通块的集合,\(T\) 是一个连通块(一棵树),\((u,v)\) 是第一条加入的边,\(siz_x\) 是此时 \(x\) 在 \(u\) 另一侧的子树 size。
这个也不是很对,我们考虑直接去钦定是哪些边作为了这个连通块的第一条边,这个时候发现,你钦定的这东西的个数,就是连通块的个数。那么钦定了 \(x\) 条这种边,首先会有 \(\binom{n}{2x}(2x-1)!!\) 种方案,接下来就让他们是 \((1,2),(3,4),\cdots,(2x-1,2x)\),然后计算这些边真的作为初始边的方案数。
那我们先不考虑容斥啥的事情,就让他们真的是所有的初始边,来试着算一下这个式子。那么剩下的所有点都得挂到这些边上,然后初始边之间是不能有连边的。发现相当于对于其他的每条边,为了不让这个初始边被其他边连过来,那么它的加入时刻不能比它相邻的初始边早。
给初始边钦定顺序并插入到操作序列,有 \(x!\) 种方案;接下来考虑最后一个被加入的初始边,所有边只要和他相邻,就必须在它之后被加入。这样的边有 \(2(n-2)\) 条;然后不和最后一条边相邻,但和倒数第二条边相邻的边,需要在倒数第二条边那里被加入。这样的边有 \(2(n-3)\) 条。
于是最终的顺序连成树形结构,其子树的 size 分别是 \(2n-3,4n-10,\cdots\)。
于是这个式子大概长成
\[\prod_{i=1}^x\frac{1}{i+\sum_{j=1}^i(2n-4j)}=\prod_{i=1}^x\frac{1}{-2i^2+(2n-1)i}=\frac{1}{x!}\prod_{i=1}^{x}\frac{1}{2n-1-2i}=\frac{(2n-3-2x)!!}{(2n-3)!!\times x!} \]但这个时候还有 \(\binom{n-2x}{2}\) 条边没有被钦定,而它们可能产生新的初始边。容斥即可。
最终我们的答案就是
\[\sum_{x=0}^{k}(-1)^{k-x}\binom{k}{x}\binom{n}{2x}(2x-1)!!\times \frac{(2n-3-2x)!!}{(2n-3)!!} \]KOI TST 2024
Day1 A
对于长为 \(m\) 的序列 \(x\),认为它是好的当且仅当 \(m\ge 2\),且 \(\max(x_1,x_m)<\min(x_2,x_3,\cdots,x_{m-1})\)。
考虑序列长为 \(n\) 的 \(a\),你可以进行任意次操作,每次可以选择一个区间 \([l,r]\) 满足 \(a_l,a_{l+1},\cdots,a_r\) 这个序列是好的,然后删除 \(a_{l+1}\cdots a_{r-1}\),接下来序列会变成 \(a_1,a_2,\cdots,a_{l-1},a_l,a_r,a_{r+1},\cdots,a_n\)。你希望最大化最终序列的所有元素的平均值。设 \(f(a)\) 为上述问题的答案。
给定长为 \(N\) 的序列 \(A\),有 \(Q\) 次询问,每次给出 \(l,r\),你需要输出 \(f(A[l\cdots r])\) 的值。具体来说,设答案化为最简分数后为 \(\frac{x}{y}\),你需要输出一行两个正整数 \(x,y\) 表示答案。
保证每次询问给出的 \(l,r\) 满足:\(A[l\cdots r]\) 是一个好的序列。
\(2\le N\le 3\times 10^5,1\le Q\le 6\times 10^5,1\le A_i\le 10^9,1\le l<r\le N\)。5s 1024MB
我真无语了,我第一次翻译的时候少翻译了一个条件(\(A[l\cdots r]\) 是好的序列),做了一万年都不会。。
考虑一次询问怎么算答案,二分答案 \(mid\),每个数 \(a_i\leftarrow a_i-mid\) 后只需要总和 \(\ge 0\)。为了输出精确分数,只需要多记录一下最优解选了几个数。设 \(f_i\) 表示前 \(i\) 个数的最大总和,\(i\) 一定不会被删除,考虑是否有一次右端点为 \(i\) 的删除,可以转移到 \(\max_{\text{valid}(j,i)}f_j+a_i\),其中 \(\text{valid}(l,r)=[\max(a_l,a_r)<\min(a_{l+1}\cdots a_{r-1})]\)。
设 \(p_i,q_i\) 分别表示左右两侧第一个 \(<a_i\) 的位置,那么 \(\text{valid}(l,r)=[q_l\ge r\land p_r\le l]\)。可以用数据结构优化。
实际上,考虑从前往后维护单调栈,把区间按照 \(a_l>a_r\) 和 \(a_l\le a_r\) 分类。如果 \([j,i]\) 合法且 \(a_j>a_i\),那么 \(j\) 一定是 \([1,i-1]\) 的一个严格后缀最小值。于是我们维护单调栈,那么以 \(i\) 为右端点的所有合法区间就是插入 \(a_i\) 时弹出的那些 \(j\) 组成的区间。那么这样的区间个数不超过 \(N\),于是总的合法的区间数量不会超过 \(2N\) 个。
于是现在我们可以对单次询问的情况做到 \(O(N\log V)\)。
注意到只需要处理所有合法区间的答案,而它们要么不交要么互相包含。于是可以对合法区间建出一棵树,设 \(f(u,j)\) 表示只考虑 \(u\) 代表的区间,保留 \(j\) 个数所能达到的最大总和。那么首先有 \(f(u,2)\leftarrow a_{l_u}+a_{r_u}\),然后我们需要对 \(u\) 的若干儿子做 max+ 卷积,最后整体加上那些一定存在的数,也就是做一个整体偏移。
由于我们只关心 \(\frac{f(u,j)}{j}\) 的 max,考虑有三个点 \(A,B,C\),坐标分别为 \((x_A,y_A),(x_B,y_B),(x_C,y_C)\),不妨设 \(x_A<x_B<x_C\),如果这三个点不形成上凸,那么可以证明 \(A,C\) 至少一个比 \(B\) 优。
于是我们只需要维护上凸壳上的点,合并时做 max 卷积直接维护闵可夫斯基和即可。这里为了能算出每个点的答案,可能不能简单地只维护凸包上的每条边,需要用平衡树维护整个凸壳上面的点来支持快速算前缀和的操作。
时间复杂度 \(O(N\log^2N+Q)\)。
https://qoj.ac/submission/394318
Day1 B
给定序列 \(a\),每次选择一个 \(i\) 满足 \(1\le i\le |a|-1\),且 \(a_i=a_{i+1}\),然后删除 \(a_i,a_{i+1}\),并在同样的位置插入 \(a_i+1\)。例如 \([2,1,1,3,2]\) 可以变成 \([2,2,3,2]\),方法是选择 \(i=2\)。
你可以对序列进行任意次操作,例如上面的序列可以接着变成 \([3,3,2]\) 再变成 \([4,2]\)。你希望最大化最终序列中所有数的最大值。定义上述问题的答案为 \(f(a)\)。
给定长为 \(N\) 的序列 \(A\),有 \(Q\) 次操作,每次操作是以下二者之一:
1 l r:输出 \(f(A[l\cdots r])\) 的值。2 p v:令 \(A_p\leftarrow v\)。\(1\le N,Q\le 10^5,1\le A_i\le 10\);对于
1操作,\(1\le v\le 10\)。
考虑一个 \(f\) 怎么算,把序列划分为相同数的极长连续段 \((x_1,c_1),(x_2,c_2),\cdots,(x_k,c_k)\),其中 \(x_i\) 是第 \(i\) 段的值,\(c_i\) 是第 \(i\) 段的元素个数。每次我们找到序列中的所有最小值,显然把它们缩起来一定不劣。
分类讨论一下,如果 \(c_i\) 是偶数,那么直接缩成 \((x_i+1,\frac{c_i}{2})\);否则这个 \((x_i,c_i)\) 左右一定不可能发生合并了,它们互相独立,于是我们可以把 \((x_i,c_i)\to (x_i+1,\frac{c_i-1}{2}),(-1,1),(x_i+1,\frac{c_i-1}{2})\),这里 \(-1\) 表示一个分隔符,它的左右互相独立。
这样每次缩完 \(a\) 中的 min(这个 min 不算 \(-1\))都至少 \(+1\),于是最多进行 \(O(\max a_i)\) 轮所有数就都相等了。这样我们可以在 \(O(n\max a_i)\) 的时间内算出一个 \(f\)。
考虑区间询问怎么做,事实上我们发现只要 \(x_i<\min(x_{i-1},x_{i+1})\),我们就一定必须得把 \((x_i,y_i)\) 化简一下。于是考虑线段树维护每个区间这样缩完之后变成什么样子即可。可以发现这样一直缩下去最终每个区间只会剩下左右两侧的各 \(O(A_i)\) 个段,以及中间可能被阻断的若干段。中间那些段显然不会再造成贡献了,只需要记录他们的 max;合并的时候处理一下是否出现新的段即可。
时间复杂度 \(O(A(N+Q\log N))\)。我偷懒写了一个 \(O(A^2(N+Q\log N))\) 的,qoj 神机给我跑过了/jy
https://qoj.ac/submission/392764
Day1 C
给定一棵 \(N\) 个点的树,第 \(i\) 条边连接 \(A_i,B_i\) 两个点,长度为 \(C_i\) 米。
现在有 \(Q\) 次询问,每次会给出两个点 \(x,y\) 和两个速度上限 \(v_x,v_y\),有一个警察和一个小偷,警察一开始在 \(x\) 点,小偷一开始在 \(y\) 点(保证 \(x\neq y\)),警察的速度上限为 \(v_x\) 米每秒,小偷的速度上限为 \(v_y\) 米每秒,在每一时刻他们都可以任意移动(可以以任意不超过速度上限的速度移动,当然也可以不动),而且可以不消耗时间地改变方向。
如果某一时刻警察和小偷在同一个位置就认为小偷被抓获(这个位置可以在一条边的中间)。
小偷希望最大化他被抓获的时间,警察希望最小化这个时间。两人每时每刻都知道对方当前的位置和速度,你需要求出如果两人都采取最优策略,小偷会在什么时候被抓获。
可以证明这个时间一定是有理数,设它化为最简分数后为 \(\frac{x}{y}\),你需要输出一行两个正整数 \(x,y\)。
\(1\le N,Q\le 10^5,1\le C_i\le 10^6,1\le v_x,v_y\le 10^6\),输入的数都是正整数。
这个题是不是糖了?考虑小偷可能会先往警察的方向走若干秒,然后从某个地方开始折返往外跑,且往回走的过程中不能被警察抓住。二分出这个分界点,那么相当于要求这个点一侧距离警察最远的一个点。分类讨论一下即可。
复杂度感觉一个 log 就行。
AtCoder mujin pc
2017 D
给定一棵 \(n\) 个节点的树,现在你需要给每条边定向,定完方向后,设 \(d(u,v)\) 表示:在这张有向图上,想要使 \(u\) 能够到达 \(v\),至少需要翻转几条边的方向。这个定向方案的代价是 \(\max_{u,v}d(u,v)\)。
你希望最小化代价。在此之上,你希望求出在 \(2^{n-1}\) 种方案中,有多少种方案能够最小化这个代价。
\(1\le n\le 3000\),答案对 \(998244353\) 取模。
首先,有简单 \(O(n^3)\) DP。
设直径长度为 \(D\),那么最小代价是 \(\lceil D/2\rceil\)。下面分类讨论:
- 直径长度为偶数
找到直径中间的那个点,以这个点为根建树,称父亲指向儿子的为正向边,儿子指向父亲的为反向边,那么每个深度恰为 \(\frac{D}{2}\) 的点到根的路径上,正向边和反向边个数之差都相等。考虑给每个点一个标号 \(w\),他满足如果 \((u,v)\) 这条边定向为 \(u\to v\) 则 \(w_v=w_u+1\);否则 \(w_v=w_u-1\)。那么所有深度恰为 \(\frac{D}{2}\) 的点的 \(w\) 值都相同,不妨钦定这些点的 \(w=0\),那么此时定向方案与合法的 \(w\) 的方案形成双射。
设 \(r\) 为直径中点,可以发现,此时一个方案合法,当且仅当对所有 \(u\),都有 \(|w_u|\le \frac{D}{2}-\text{dist}(u,r)\)。首先必要性是显然的,然后注意到 \(d(u,v)\le \frac{w_u-w_v+\text{dist}(u,v)}{2}\)(当 \(\text{LCA}(u,v)=r\) 时取等号),于是
\[\begin{aligned} d(u,v)&\le \frac{w_u-w_v+\text{dist}(u,v)}{2}\le \frac{|w_u|+|w_v|+\text{dist}(u,v)}{2} \\&\le \frac{D+\text{dist}(u,v)-\text{dist}(u,r)-\text{dist}(v,r)}{2}\le \frac{D}{2} \end{aligned} \]于是充分性得证。于是我们直接 DP 即可,复杂度 \(O(n^2)\)。
- 直径长度为奇数
找到直径中间的那条边 \((r_1,r_2)\),设 \(r_1\) 一侧的点集为 \(S_1\),\(r_2\) 一侧的点集为 \(S_2\),类似地给每个点标号 \(w\),和上述情况类似,只不过这次根据中间那条边的朝向,可能会有某一侧的点集的约束需要额外 \(-1\) 也就是更严一点。
类似地也可以做到 \(O(n^2)\)。
2018 H
考虑 \(H\times W\) 的网格,现在你需要给每个格子黑白染色。定义一种染色方案合法,当且仅当能够用 \(1\times 2\) 的纸条不重叠且不超出网格边界地恰好覆盖所有白色格子,恰好不覆盖所有黑色格子。
求合法染色方案数对 \(998244353\) 取模的值。\(1\le H\le 5,1\le W\le 10^9\)。
这个题是不是糖了?考虑怎么判合法,发现需要记录最后一行还没填入的白色格子 \(S\)。
那么再套一层就是把这些全压进来。看上去状态数有 \(2^{2^H}\) 个,但是毛估估一下就不是很多。
这里直接搜大概会得到 \(H=5,6,7,8\) 状态数分别为 \(91,318,1223,5085\);但我们注意到只需要考虑当前最后一行已经填到没有相邻空位的那些状态,这样可以大大减少状态数,分别为 \(26,61,169,520\)。
搬云斗了
Singapore NOI 2024
D
有一个 \(1,2,\cdots,n\) 的排列 \(p\)。你并不知道这个排列 \(p\) 是什么。
现在给出 \(m\) 条信息 \(x,y\),表示可以确定 \(p_x<p_y\)。
对每个 \(i=1,2,\cdots,n\),输出最小的 \(k\) 满足:可以用前 \(k\) 条信息推出 \(p_i\) 的值。
如果不存在这样的 \(k\),输出 \(-1\)。保证存在至少一个排列符合所有约束。
\(2\le n\le 2\times 10^5,1\le m\le 8\times 10^5\)。
首先,我们在最终的图中找到一个拓扑序,然后对这个排列做一下置换。下面我们钦定每次给出的 \(x,y\) 都满足 \(x<y\);一个数 \(x\) 当前能被确定,当且仅当它能到达 \(x-1\) 个点,且有 \(n-x\) 个点能到达它。
我们考虑 \(x-1\),发现他必须得能从 \(x\) 直接到达;进一步考虑 \(x-2\),发现它的入边里面至少得有 \(x-1\) 或 \(x\)。
依此类推,我们可以发现,如果设 \(a_i\) 表示 \(i\) 的入边中编号最小的点,那么 \(x\) 能到达 \(1,2,\cdots,x-1\),当且仅当对所有的 \(i=1,2,\cdots,x-1\),都有 \(a_i\le x\)。同理设 \(b_i\) 表示 \(i\) 的出边中编号最大的点,那么还需要对所有的 \(i>x\),都有 \(b_i\ge x\)。
每次修改对 \(a,b\) 的影响是 \(O(1)\) 的,简单用线段树维护下就行。时间复杂度 \(O((n+m)\log n)\)。
E
有一个无限大的二维平面,你一开始在 \((0,0)\)。你每一秒可以向上下左右移动 \(1\) 的距离,也就是说这一秒如果你在 \((x,y)\),那么下一秒你可以走到 \((x-1,y),(x+1,y),(x,y-1),(x,y+1)\) 中的一个。
给定 \(n\) 个矩形,第 \(i\) 个矩形可以用 \(a_i,b_i,c_i,d_i\) 表示,意思是所有满足 \(a_i\le x\le b_i,c_i\le y\le d_i\) 的点都被移除了,不可以经过。这些矩形可能会互相重叠。
设 \(d(x,y)\) 表示走到 \((x,y)\) 所需的最短时间。如果走不到 \((x,y)\),则 \(d(x,y)=-1\)。特别地,\(d(0,0)=0\)。
现在有 \(q\) 次询问,询问有两种:
1 x y:输出 \(d(x,y)\) 的值。2 m:输出有多少个 \((x,y)\) 满足 \(0\le d(x,y)\le m\)。\(1\le n\le 400,1\le q\le 2\times 10^5,-10^9\le a_i\le b_i\le 10^9,-10^9\le c_i\le d_i\le 10^9\)。
对于第 \(1\) 种询问,\(-10^9\le x,y\le 10^9\);对于第二种询问,\(1\le m\le 10^9\)。
保证 \((0,0)\) 不被任何矩形覆盖;输入的数都是整数。
题解看上去很恐怖。。。
Luogu9521
给定 \(n,m\) 和序列 \(a_1,a_2,\cdots,a_n,b_1,b_2,\cdots,b_m\),有一个 \(n\times m\) 的网格图,每条边有边权,其中 \((i,j)\to (i,j+1)\) 边权为 \(a_i\),\((i,j)\to (i+1,j)\) 边权为 \(b_j\)。
现在要从 \((1,1)\) 走到 \((n,m)\),最小化边权和。\(1\le n,m\le 10^5,1\le a_i,b_i\le 10^9\)。
考虑一个 \(L_a\times L_b\) 的矩形,横着的两条边边权上下分别为 \(a_1,a_2\),竖着的左右分别为 \(b_1,b_2\),那么可以发现我们比的是 \(a_1\times L_a+b_2\times L_b\) 和 \(a_2\times L_a+b_1\times L_b\)。做差得到
\[(a_1-a_2)L_a+(b_2-b_1)L_b>0\iff \frac{a_1-a_2}{L_b}>\frac{b_1-b_2}{L_a} \]也就是说,如果 \(a\) 那边的斜率更大,那么就应该先横着走;否则就竖着走。
这也就是说,最优解中的每一条折线,都应该满足,他先走的是斜率小的那一侧。
此时有一个 \(O((n+m)\log (n+m))\) 的做法:每次找到全局最大的差分位置,然后消掉所有不可能的拐点。这样最后路径只会剩下一条,用 std::set 维护即可。官方题解里有详细的图解。
事实上,考虑三个点 \((i,a_i),(j,a_j),(k,a_k)\),如果他们不形成下凸,那么 \(i,j\) 之间的斜率比 \(j,k\) 之间要小,也就是说如果我们某一步选择了先走 \(i\to j\) 那么一定会立刻走 \(j\to k\),于是我们可以直接把路径缩成 \(i\to k\)。于是只需要求出 \(a,b\) 的下凸壳,每次走斜率小的一边即可。复杂度 \(O(n+m)\)。
LuoguP5972
好像是我初二的时候提出的一个问题,当时 u 群有人说存在 \(O(n^23^{n/3})\) 做法,昨天晚上突然会做了!
考虑从前往后 DP,暴力是记录 \(S\) 表示目前选择的数的集合,这样状态数仍然是 \(O(2^n)\) 级别。
但我们注意到,设 \(i\) 后面的数分别为 \(x_1,x_2,\cdots,x_k\),我们只关心 \([1,x_1),(x_1,x_2),\cdots,(x_k,n]\) 这些每一段中选了多少个数。于是状态数不会超过每段长度 \(+1\) 的乘积,由柯西不等式可以知道一定在段长相同时取到最值,直接看成连续的情况来分析,简单求导可以得到最值在 \(e^{n/e}\),由于问题是离散的于是最值大约是 \(\max(2^{n/2},3^{n/3})\)。
于是直接 DP 就可以了。时间复杂度是 \(O(n^23^{n/3})\),使用 map 或许会被卡常,手写哈希表可以稳过。
LOJ3490
只会 \(O(n^3m+q)\) 左右的做法,紫砂了。
大概是把所有分段函数都求出来,之类的,每一段会形如一段平的或者斜率为 \(-1\) 的东西。
等会儿,打赢复活赛了,考虑怎么算 \(s\to t\) 不能等待任何一天情况下的最短路,发现这个情况下,我们不妨钦定它就得被某条边卡住,也就是在 \(C-L\) 时刻到达这里,然后在 \(C\) 时刻离开。如果没有被卡住,我们知道这段斜率是平的,那算出来的值也是对的。
然后再考虑等待至少一天的最短路,钦定那条第一次等待的边,也是类似的。那么首先我们算出每条边 \(C\) 时刻以及 \(L\) 时刻离开之后到每个点的最短路,这部分跑 \(m\) 次 dij 有复杂度 \(O(m(n+m))\),然后再反着跑 dij,最后 \(q\) 次询问只需要二分找后缀最小值即可,复杂度 \(O(n^2m+m^2+q\log n)\)。
首先,我们有 \(O(q(n^2+m))\) 的算法,即每次跑一遍 dijkstra,同时记录到每个点的最短路以及这个最短路对应的时刻。可以证明只要这样就能得到最优解。
把路径分成两类:在一天内完成的,和至少有一次等待到下一天的。
对于在一天内完成的路径,我们考虑找到其中限制最严(也就是经过这条边的时间最接近他的限制时间)的一条边 \((u,v,L,C)\),假设我们是从 \(s\) 走到 \(t\),起始时间为 \(A\),如果走到点 \(u\) 的时候时刻为 \(B\le C-L\),那么我们知道这条边的 \(C-L-B\) 是所有边里面最小的一个。
我们把起始时刻加上 \(C-L-B\),可以发现路径仍然合法。于是有如下的算法:枚举每条边 \((u,v,L,C)\),计算 \(dis_x\) 表示想要从 \(x\) 走到 \(u\),满足:
- 整个过程必须在一天内完成。
- 到达 \(u\) 时,当前时刻 \(\le C-L\)。
这种情况下所需的最小时间。这可以通过一遍 dijkstra 在 \(O(n^2+m)\) 的时间内算出,同时也可以算出 \(tim_x\) 表示如果要求能走这个最短路,\(x\) 的起始时间最晚是多少。再通过一遍 dijkstra 算出 \(to_y\) 表示从 \(v\) 到 \(y\),起始时间为 \(C\),所需的最少时间(这个过程同样必须在一天内完成)。
算出这些之后,我们就可以计算 \((u,v,L,C)\) 这条边对所有点对 \((x,y)\) 的贡献,即对于起始时间 \(A\le tim_x\),都有一种 \(dis_x+to_y+L\) 的方案。
现在考虑跨越多天的路径,注意到如果在某个城市 \(u\) 进行等待,一定是等待到第二天的 \(0\) 时刻,然后在 \(L\) 时刻出现在某条边 \((u,v,L,C)\) 的终点 \(v\)。
于是类似地,我们枚举路径上第一条进行等待的边 \((u,v,L,C)\),同理算出 \(tim,dis,to\)(只不过此时从 \(v\) 开始走的时候,我们允许它跨越多天完成),更新答案即可。
最后再对每个点对 \(x,y\),我们把贡献到 \((x,y)\) 上面的若干条路径按照 \(tim\) 排序,然后预处理后缀 min,即可在 \(O(\log n)\) 的时间内回答一组询问。这里可能要对 \(O(n^2)\) 个长度为 \(O(m)\) 的数组排序,但注意到对于一个 \(x\),所有 \(y\) 的分段点总共只有 \(O(m)\) 个,于是只需要进行 \(n\) 次排序。
综上,总复杂度 \(O((n^2+m)m+nm\log m+q\log n)\)。
QOJ2573
给定 \(n,P\),对每个 \(s=0,1,\cdots,n^2\) 求出:
- 有多少个长为 \(n\) 的排列 \(p\) 满足 \(\sum_{i=1}^n\max(p_i,i)=s\)。
答案对 \(P\) 取模。\(1\le n\le 150,10^8\le P\le 10^9+7,P\) 是质数。
考虑转化为有多少对长为 \(n\) 的排列 \((p,q)\),满足 \(\sum_{i=1}^n\max(p_i,q_i)=k\),然后把答案除掉 \(n!\)。
从大到小填数,设 \(f(i,j,s)\) 表示填了 \(i,i+1,\cdots,n\),目前有 \(j\) 个位置重叠,总和为 \(s\) 的方案数。
考虑如何转移 \(f(i+1,j,s)\to f(i,j,\cdot)\)。
算出未重叠的部分个数为 \(k=n-i-j\),新填入两个 \(i\),那么有如下方案:
- \(p\) 那边填到和 \(q\) 重叠的位置,\(q\) 那边也和 \(p\) 重叠:\(f(i+1,j,s)\times k^2\to f(i,j+2,s)\)
- \(p\) 填到和 \(q\) 重叠的位置,\(q\) 和 \(p\) 不重叠:\(f(i+1,j,s)\times k\times (n-j-2k)\to f(i,j+1,s+i)\)
- \(p\) 不重叠,\(q\) 重叠:\(f(i+1,j,s)\times k\times (n-j-2k)\to f(i,j+1,s+i)\)
- 两边都不重叠,但新填入的两个 \(i\) 位置相同:\(f(i+1,j,s)\times (n-j-2k)\to f(i,j+1,s+i)\)
- 两边都不重叠且两个 \(i\) 位置不相同:\(f(i+1,j,s)\times 2\times \binom{n-j-2k}{2}\to f(i,j,s+2i)\)
综上本题在 \(O(n^4)\) 时间内解决。
胖朵说:从小到大插入每个数,维护当前的置换环形态,考虑置换环每条边的贡献,记录 \(f_{i,j,s}\) 表示当前插入到 \(i\),有 \(j\) 个置换环现在还长成链的样子,目前所有边的贡献之和为 \(s\)。转移有:
- \(i\) 独自新开一个点,然后还需要再分要不要和自己连成自环两种情况。
- \(i\) 连接两条链。
- \(i\) 把一条链变成了一个环。
这样不用除掉 \(n!\),嗯
QOJ2568 加好多 0
对于一个 \(n\times m\) 的矩阵 \(a\),其中每个 \(a_{i,j}\) 都是非负整数,你需要找到一条 \((1,1)\) 到 \((n,m)\) 的路径,满足每一步只能向右或向下走(即 \((i,j)\to (i,j+1),(i,j)\to (i+1,j)\)),你希望最大化这条路径所经过的格子上的 \(a\) 之和。定义上述问题的答案为 \(f(a)\)。
有 \(q\) 次询问,每次给出 \(n,m,k\),问有多少个 \(n\times m\) 的矩阵 \(a\) 满足 \(f(a)=k\)。
答案对 \(998244353\) 取模。
\(1\le n,m,k\le 5\times 10^6,1\le q\le 10^6\)。
首先我们把 \(f(a)=k\) 放宽成 \(f(a)\le k\)。
考虑一个 \(f(a)\) 怎么算,设 \(dp_{i,j}\) 表示走到 \((i,j)\) 的最小代价,有
\[dp_{i,j}=\max(dp_{i-1,j},dp_{i,j-1})+a_{i,j} \]我们发现,实际上 \(a\) 矩阵和 \(dp\) 矩阵是一一对应的关系,如果确定了 \(dp\),那么有
\[a_{i,j}=dp_{i,j}-\max(dp_{i-1,j},dp_{i,j-1}) \]于是我们考虑对合法的 \(dp\) 矩阵计数。
那么只需要 \(dp_{n,m}\in[0,k]\),而且需要满足 \(dp_{i,j}\ge \max(dp_{i-1,j},dp_{i,j-1})\)。
这是一个经典问题,我们考虑对每个 \(0\le i<k\) 画出 \(\le i\) 的部分和 \(>i\) 的部分的分界线,那么它们几乎构成了 \(k\) 条 \((0,m)\) 到 \((n,0)\) 的路径组,但它们可能会相交。我们考虑把第 \(i\) 条线向右下移动 \(i-1\) 格,那么就可以得到 \(k\) 条 \((x,m+x)\) 到 \((n+y,y)\) 的不相交路径组。使用 LGV 引理求解,时间复杂度为 \(O(n+m+k^3)\)。
实际上,可以证明该矩阵的行列式为(或者运用杨表相关结论,也可以得到):
\[\prod_{i=1}^n\prod_{j=1}^m\prod_{l=1}^k\frac{i+j+l-1}{i+j+l-2} \]注意到 \(i+j+l\le n+m+k\),我们对每个 \(p\le n+m+k\) 计算其系数 \(c_p\),则答案为 \(\prod_{p=3}^{n+m+k}\left(\frac{p-1}{p-2}\right)^{c_p}\),其中 \(c_p\) 是 \(1\le i\le n,1\le j\le m,1\le l\le k\) 且 \(i+j+l=p\) 的 \((i,j,l)\) 个数。\(c_p\) 可以使用容斥原理计算,拆开后发现只需要算若干 \(\prod_{i=1}^x i!\) 以及它们的逆元这样的形式。
于是可以在 \(O(n+m+k+q)\) 的时间内解决这个问题。
Luogu8114
和上题一模一样哈哈
LOJ3695
对于一个区间 \([l,r]\),如果 \(\sum_{i=l}^ra_i<\min(a_{l-1},a_{r+1})\),称这样的区间 \([l,r]\) 为阻塞区间。
这里认为 \(a_0=a_{n+1}=\infty\)。
首先有一些显然的性质:阻塞区间的个数不超过 \(2n\),且两个阻塞区间要么包含,要么不交。考虑一次询问 \([L,R]\),发现如果 \(i\) 不合法了,意味着有一个阻塞区间 \(i\in[l,r]\subseteq [L,R]\) 使得它不合法了。同理也可以发现,如果不存在包含 \(i\) 的阻塞区间,那么 \(i\) 一定合法。
考虑直接用线段树维护当前节点 \([L,R]\) 内还有多少个点没有被阻塞区间覆盖。合并的时候,有可能左边的一段后缀和右边的一段前缀本来都是阻塞区间,但它们合并起来之后就合法了。注意到这些区间的个数不超过 \(O(\log V)\),而且这些区间之间都是互相相交的,我们只需要找到最大的一个阻塞区间。双指针即可。
综上,时间复杂度 \(O(N\log V+Q\log N\log V)\),其中 \(V=10^9\) 为值域。
我比较懒,代码写的多了一个 \(\log V\),看上去跑的也非常快啊,最慢的点才 0.8s 左右。
QOJ4805
给定一个 \(n\) 点 \(m\) 边的无向图,第 \(i\) 个点上有一个标号 \(p_i\),其中保证 \(p_1,p_2,\cdots,p_n\) 是一个 \(1\) 到 \(n\) 的排列。
再给定两个点 \(A,B\)(\(1\le A,B\le n,A\neq B\)),认为一个标号方案 \(p\) 是好的,当且仅当:
- 对每个节点 \(x\),都存在一条从 \(A\) 开始,到 \(B\) 结束的路径,满足这条路径经过 \(x\),且路径上的点的标号严格递增。
一开始这张图不一定是好的,你可以进行至多 \(999\) 次操作,每次操作可以选择一条从 \(A\) 开始的简单路径,然后把它们的标号循环左移一位。具体来说,如果你选择的路径是 \(x_0(=A),x_1,\cdots,x_{k-1}\),设 \(y_i=p_{x_i}\)(\(0\le i\le k-1\)),操作完之后,所有 \(p_{x_i}\) 会同时变成 \(y_{(i+1)\bmod\ k}\)。
\(2\le n\le 1000,1\le m\le 2000,1\le A,B\le n,A\neq B\)。
首先有解需要缩点之后圆方树形成一条链,且 \(A,B\) 分别在两端。
于是我们考虑先构造一个这张图 \(A\to B\) 的双极定向,然后在双极定向得到的 DAG 上按照拓扑序逆序考虑每个点,动态维护点集 \(S\),保证 \(S\) 中的每个点到 \(B\) 的路径上点权均递增。初始 \(S=\{B\}\),考虑依次加入每个点 \(u\),那么进行 \(n\) 次之后,点集就会变成 \(\{1,2,\cdots,n\}\)。
现在的问题是,有可能加入的这个点 \(u\) 的点权会比它的后继要大。我们任取一条 \(A\to u\) 的路径,易知此时 \(A\to u\) 路径上的所有点目前都不在 \(S\) 内。找到 \(u\) 的后继中点权最小的一个点 \(v\),讨论一下:
- 如果 \(p_v>p_A\),那么我们直接对 \(A\) 到 \(u\) 这条路径 shift 一下,那么新的 \(p_u\) 变成了 \(p_A\),而且这个值比他的后继节点的点权都要小。
- 如果 \(p_v<p_A\),我们把 \(v\) 也加入到操作路径的末尾,然后接着从 \(v\) 开始找,直到满足上面的条件,或者 \(u=B\)。此时,考虑我们第一次找到某个 \(x\) 满足 \(x\) 的所有后继节点权值都 \(>p_A\) 的这个时候,会把路径 \(A\to x\) 整体左移,那么新的 \(p_u\) 就变成了 \(p_v\),由于 \(p_v\) 是原先 \(u\) 的后继中点权最小的节点,于是它小于 \(u\) 的其他后继节点的点权;另一方面新的 \(p_v\) 变成了 \(v\) 的某个后继 \(w\) 的 \(p_w\),由于原先 \(v,w\in S\),所以必有 \(p_v<p_w\)。类似地,此时每个节点都会满足条件。
综上我们成功用一次操作完成了扩展,于是只需要 \(n-1\) 次操作就可以把 \(S\) 扩展到整个集合 \(\{1,2,\cdots,n\}\)。
算法的时间复杂度为 \(O(n^2)\),操作次数为 \(n-1\)。
幽蝶能留一缕芳
只关注 \(1\to 2\) 什么时候可行,然后把答案乘上 \(N(N-1)\)。
- \(1,2\) 都在环外
那么 \(dis=k\) 的方案数是
\[ans_k=(k+1)\times (n-2)^{\underline{k-1}}\times \sum_{m=k+1}^{n-1}m^{m-k-2}\binom{n-k-1}{m-k-1}(n-m)^{n-m+1}\\ \]这个怎么优化?草了,改一下枚举对象,得到
\[ans_k=\sum_{m=k+2}^nn^{n-m}(n-2)^{\underline{m-2}}(m-k-1) \]这个倒是好优化。
对于一个 \(L\),不难算出最小的合法的 \(R\) 是
\[L+\left\lceil\frac{k\bmod L}{\lfloor k/L\rfloor}\right\rceil \]于是合法的 \(L,R\) 数量是 \(f_k=\sum_{L=1}^kn-(L+\lceil\frac{k\ \bmod \ L}{\lfloor k/L\rfloor}\rceil)+1\),这部分可以用整除分块优化。
- \(2\) 在环内
发现只要能同时走 \(p,p+1\),由于 \(\gcd(p,p+1)=1\) 我们肯定能走回来。
于是 \(R\ge L+1\) 的 case,都一定合法;否则设环长为 \(m\),\(dis(1,2)=k\),那么需要 \(\gcd(m,L)\mid k\)。
可以枚举约数计算。考虑怎么算方案数。这个简单很多啊是不是,也是和上面类似的东西。
这样总复杂度就 \(O(n\sqrt{n})\)。唉这个题真的是,我写了一上午
LOJ3685
没看到要求是最短路径,我说这不是 circus P 吗
那要求最短路径的话,猜一下,如果合法那么存在一种方案使得,每个人都是开始走之后,立刻直接走完。
这个怎么判呢,感觉一下,如果 \((i,j)\) 满足 \(S_i\in\text{path}(S_j,T_j)\) 或者 \(T_j\in \text{path}(S_i,T_i)\),那么 \(i\) 就得在 \(j\) 前面走。这样会连出来一张有向图,如果是 DAG 就有解,否则无解。
但是边数还是 \(O(m^2)\) 怎么办呢,考虑随便拉个数据结构优化建图,就可以做到 \(O(m\log n)\)。
考虑寻找合法解的性质,发现如果有解,那么一定存在一种方案使得每个人开始走之后,直接不停顿地走到终点。
证明:考虑合法解中某个人 \(i\) 的相邻两次行动 \(A\to B,B\to C\),由于走的是最短路径,必有 \(A\neq B\neq C\)。
我们考虑如果这两次行动在总的行动序列上不相邻,它们中间有若干次行动,由于此时 \(i\) 位于点 \(B\),因此其他人的任意行动都不能经过 \(B\)。以 \(B\) 为根建树,那么中间的行动可以划分为三部分:
- 完全在 \(A\) 子树内的部分
- 完全在 \(C\) 子树内的部分
- 其他的部分
借用官方题解的图:
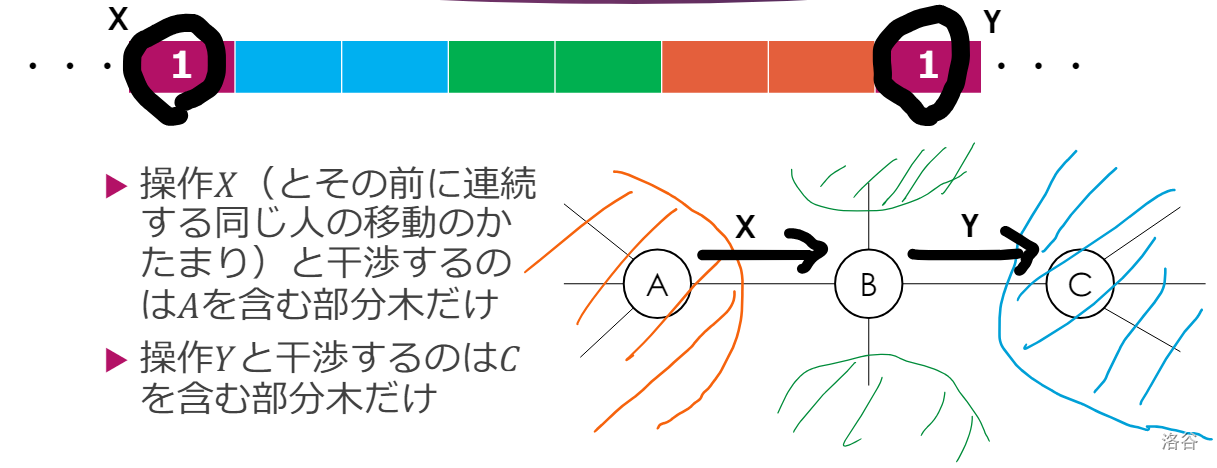
于是我们可以重排操作序列为:
- 先进行完全在 \(C\) 子树内的部分。
- 然后让 \(i\) 这个人从 \(A\to B\to C\)。
- 然后进行 \(A\) 子树内的部分和其他部分。
这样一直操作下去,一定可以构造出一种解满足每个人开始走之后,直接不停顿地走到终点。
于是我们考虑两个人 \((i,j)\) 如果满足 \(S_i\in\text{path}(S_j,T_j)\) 或者 \(T_j\in \text{path}(S_i,T_i)\),那么 \(i\) 就得在 \(j\) 前面走。这样会连出来一张有向图,如果是 DAG 就有解,否则无解。
直接连会得到 \(O(M^2)\) 条边,许多数据结构都能将其边数优化至 \(O(M\log N)\)。
LOJ3687
首先,当 \(i<j\) 时,\(T_i\le T_j\) 等价于 \(s[i+1,j]\le s[i,j-1]\)。
也就是说,区间 \([i,j-1]\) 内第一个满足 \(s_k\neq s_{k+1}\) 的位置 \(k\) 需要满足 \(s_k\ge s_{k+1}\)。
另一方面,如果 \(i>j\),那么相当于区间 \([j,i-1]\) 内第一个满足 \(s_k\neq s_{k+1}\) 的位置 \(k\) 满足 \(s_k\le s_{k+1}\)。
称 \(i<j\) 的限制 \(T_i\le T_j\) 为第一类约束区间 \([i,j-1]\),否则为第二类约束区间 \([j,i-1]\)。
直接记录 \(f(i,j)\) 表示前 \(i\) 个字符,\(s_i=j\) 的方案数。转移时,我们分三种情况讨论:
- \(s_i=s_{i+1}\):此时没有约束,直接转移 \(f(i,j)\to f(i+1,j)\)。
- \(s_i>s_{i+1}\):枚举上一个 \(s_k\neq s_{k+1}\) 的位置 \(k\),那么要求 \(i\) 能满足所有 \(l>k,r\ge i\) 的 \([l,r]\) 的约束,也就是不能存在第二类约束区间,满足 \(k<l\le i,r\ge i\)。合法的 \(k\) 是一段后缀,可以拿 set 简单维护得到这段后缀。得到合法后缀之后有 \(f(k+1,j)-f(k,j)\to f(i+1,[x<j])\),可以简单做到 \(O(1)\) 转移。
- \(s_i<s_{i+1}\):类似。
综上,总复杂度 \(O(n|\Sigma|+n\log n)\),其中 \(|\Sigma|=26\)。
LOJ3688
显然任意时刻 \(X,Y\) 肯定是最终串的一个区间,因此我们考虑区间 DP。
设 \(f(l,r)\) 表示合成 \([l,r]\) 所需的最小代价,分最后一次有效操作是粘贴还是加字符讨论。
如果是加字符,有 \(f(l,r)\leftarrow f(l,r-1)+A\)。
如果是粘贴,那么如果粘贴了一个 \([k+1,r]\),考虑到剪切的时候会直接变成空串,于是我们一定是先用最小代价构造出 \(s[k+1,r]\),然后需要算出,如果剪贴板里面是 \(s[k+1,r]\),那么构造出 \(s[l,r]\) 最少需要多少代价。
如果粘贴一次还不如直接加字符,即 \(A\times (r-k)<C\),那显然没有用。
否则我们应该粘贴尽可能多次,也就是说要在 \([l,r]\) 中找到尽可能多的不交子串 \(s[k+1,r]\)。
考虑先枚举 \(r\),然后枚举 \(k\),对所有的 \(l\) 做贡献。枚举完 \(r,k\) 之后,设 \(c_i\)(\(i\le r\))为 \([i,r]\) 中子串 \([k+1,r]\) 的最多不交出现次数,我们相当于要做转移
\[f(k+1,r)+B+(r-l+1-c_l\times (r-k))\times A+c_l\times C\to f(l,r) \]注意到 \(c_i\le \frac{r}{r-k}\),考虑对一段相同的 \(c_l\) 一起做贡献,那么是一个区间对公差为 \(A\) 的等差数列 chkmin 的形式,可以简单维护。这样对一个 \(r\),只需要 \(O(r\log r)\) 次区间 chkmin。进一步发现区间可以放宽成前缀,于是可以 \(O(1)\) 进行一次操作。
现在还需要求一个 \(p\) 前面 \([l,r]\) 最后一次出现的位置,注意我们会对一个 \([l,r]\) 询问若干递减的 \(p\),在 SAM 上定位到 \([l,r]\) 这个节点,然后在 endpos 集合里维护一个指针即可做到均摊 \(O(1)\)。
综上,总复杂度 \(O(N^2\log N)\)。
LOJ3690
这什么垃圾啊?
按 \(X\) 排序,钦定 \(X\) 最大的为 \(i\),那么需要选出 \(j,k\) 满足 \(j,k<i\),且 \(Y_j>\max(Y_k,Y_i),Z_k>\max(Z_j,Z_i)\)。
动态维护当前集合 \(S\),每次加入一个 \((Y_i,Z_i)\),先钦定他的 \(Y\) 最大,那么剩下那个人的 \(Z\) 尽可能大肯定最优,只需要查询 \(Y_j<Y_i\) 的 \(Z_j\) 的最大值。把这个 \((Y_i,Z_j)\) 加入答案集合 \(T\),类似地也对 \(Z\) 做一遍,每次查询时,只需要查询右上角的 max。是三维偏序的形式,使用任意数据结构即可简单做到 \(O(N\log^2N)\)。
我是弱智。这我得坐起来跟他打。
考虑直接取出 \(X,Y,Z\) 最大的三个,发现如果有一个 \(i\) 满足他的两维都是 max,那么这个 \(i\) 不可能在答案中,我们删掉这个 \(i\),然后接着做下去;否则这个就是答案。时间复杂度 \(O(N\log N)\)。
LOJ3692
这什么垃圾啊?等会儿,感觉这个 \(O((N+Q)D)\) 还算有意思,还是坐起来跟他打吧
大概想了一些别的做法,比如说点分树可以 \(O((N+Q)\log^2N)\);考虑用一下 \(D\le 40\),每个点开一个长为 \(D\) 的分治结构。为了去除同子树贡献,有一些解决方案:对每个点的儿子再开一个分治结构,或者是单独把贡献减掉。由于 \(L\) 不一定是质数,没办法求逆元;但是注意只有乘除法,我们可以对 \(L\) 的每个质因子单独维护指数,这样做一次运算会多带上 \(\omega(L)\) 的复杂度。
于是有 \(O(N+QD\log D\log N)\) 或者 \(O(N+QD\omega(L)\log D)\) 等等做法。
对于修改,如果修改了和 \(u\) 距离不超过 \(D\) 的一个点 \(v\),我们发现在 \(\text{LCA}(u,v)\) 处计算贡献似乎不可避免地要带上 log。设 \(\text{dist}(u,v)=x\le D\),我们考虑在 \(\text{LCA}\) 的 \(\lfloor\frac{D-x}{2}\rfloor\) 级祖先 \(p\) 的位置计算贡献。
那么要求 \(\text{dist}(u,p)+\text{dist}(p,v)=D\) 或者 \(D-1\)。可以发现,这样的确能不重不漏地统计完所有贡献。具体来说,对每个点 \(u\) 我们记录 \(f_{u,i}\) 表示 \(u\) 子树内和他距离为 \(i\) 的所有点进行的修改。修改时我们枚举 \(u\) 的祖先 \(p\),将 \(f_{p,D-\text{dist}(u,p)}\) 和 \(f_{p,D-1-\text{dist}(u,p)}\) 计入这次贡献。查询时枚举 \(v\) 的祖先 \(p\),把 \(f_{p,\text{dist}(u,p)}\) 累计进答案。
有一个细节是 \(\text{LCA}\) 可能不存在 \(\lfloor\frac{D-x}{2}\rfloor\) 级祖先,我们在根节点往上再加 \(D\) 个点即可。
总复杂度 \(O((N+Q)D)\)。常数非常小,目测应该比我上面扯的那些做法要快很多。
CF1400F
考虑直接 DP 最后保留的数构成的子序列,有一个暴力 DP 是,\(f_{i,S}\) 表示前 \(i\) 个数,目前序列最长的一个和 \(\le x\) 的后缀里面的数为序列 \(S\),最多能留几个数。但是 \(S\) 的状态数可以有 \(2^x\) 种。
草了,冲一下这个做法,欸,怎么 TLE 了啊?
思考。看上去他真的把我 \(2^x\) 几乎卡满了,这么有实力?
那说明合法的状态其实比不合法的状态要多特别多,我可以只考虑把所有不合法的状态拎出来然后相当于不能匹配上他们中的任何一个。建一下 ACAM 直接做就好了。
QOJ7185
给定一个二分图,左边有 \(n\) 个点,右边有 \(m\) 个点,右边每个点有容量,左边第 \(i\) 个点和右边第 \(j\) 个点之间的边权为 \(c_{i,j}\)。对每个 \(k=1,2,\cdots,n\),求流量为 \(k\) 的最小费用流。
\(1\le n\le 50000,1\le m\le 10,1\le c_{i,j}\le 10^9\)。
首先建出费用流图,把 \(s,t\) 和右边的 \(m\) 个点称作关键点。
考虑维护每两个关键点之间不经过其他关键点的可能路径集合,这样每次我们在增广时如果要求出 \(s\to t\) 的最短路,只需要在关键点之间跑最短路。
考虑得到一个增广路之后如何模拟增广,注意到我们不需要考虑和 \(s,t\) 相关的反向边,因此关键点之间不经过其他关键点的最短路形态实际上相当简单,本质上只有以下几种:
- \(s\) 到某个右部点 \(R_j\):经过某个还未匹配的 \(L_i\),路径形如 \(s\to L_i\to R_j\)。
- 右部点之间:\(R_j\to L_i\to R_k\)。这里一定只会经过一个左部点,因为不能经过别的右部点。
- 右部点到 \(t\):直接走 \(R_j\to t\)。
我们可以在每个左部点 \(L_i\) 处把经过 \(L_i\) 的路径的贡献算进去。
由于我们找到的最短路的长度也是 \(O(m)\) 级别,对这条最短路经过的左部点重新计算它们的贡献即可。
求最短路每次需要 \(O(m^2\log n)\) 建边,然后 \(O(m^3)\) 求解最短路;重新计算左部点贡献时,每个左部点最多只有两条邻边会翻转,只会影响 \(O(m)\) 种决策。一共只有 \(O(m)\) 个左部点,故这部分复杂度也是 \(O(m^2\log n)\)。
综上,本题在 \(O(n(m^2\log n+m^3))\) 时间内解决。
AGC018C Coins
反悔贪心可以导出一个做法。考虑建图跑费用流:
左边建 \(n\) 个点 \(P_1,P_2,\cdots,P_N\),连边 \(s\to P_i\),边权 \(0\) 容量 \(1\)。
右边建三个点 \(A,B,C\),都连到 \(t\),边权 \(0\) 容量分别为 \(X,Y,Z\)。
每个 \(P_i\) 连三条边 \(P_i\to A,B,C\),边权分别为 \(a_i,b_i,c_i\),容量为 \(1\)。
于是就变成了 QOJ7185,套过来就行。这里 \(n\le 10^5,m\le 3\)。
https://atcoder.jp/contests/agc018/submissions/52902728
[NOI2019] 序列
每个点有四种决策:两边都不选,\(a\) 那边选,\(b\) 那边选,\(a,b\) 同时选。
对后三种决策建出三个点 \(Q_{1\cdots 3}\),但是我们发现没办法直接确定某个 \(Q_i\to t\) 的流量。
具体来说我们实际的约束是:
- \(Q_3\to t\) 的流量 \(\ge L\);
- \(Q_1\to t,Q_3\to t\) 的流量之和为 \(K\);
- \(Q_2\to t,Q_3\to t\) 的流量之和为 \(K\)。
朴素的想法是枚举 \(Q_3\to t\) 的流量 \(d\ge L\),可以得到 \(Q_1,Q_2\to t\) 的流量均为 \(K-d\),然后跑 QOJ7185。
但是每次跑一遍复杂度至少为平方,考虑 \(d\) 每增加 \(1\),相当于我们要进行两次退流 \(t\to Q_1\to s,t\to Q_2\to s\),再进行一次增广 \(s\to Q_3\to t\)。对于增广我们正常做,对于退流改成求 \(t\to s\) 的最长路即可。
此时由于我们反过来要求 \(t\to s\) 的最长路,还需要额外维护 \(Q_i\to s\) 的最长路。
总复杂度仍然是 \(O(n\log n)\)。 这个做法的常数有点大...不太能过的样子QAQ
AGC034D Manhattan Max Matching
设 \(M\) 为红球总数。考虑把 \(|x_i-x_j|+|y_i-y_j|\) 拆成
\[\max(x_i-x_j+y_i-y_j,x_i-x_j+y_j-y_i,x_j-x_i+y_i-y_j,x_j-x_i+y_j-y_i) \]那么会得到四种符号,我们在中间建四个点分别表示 \((+,+),(+,-),(-,+),(-,-)\) 四种符号。
接下来对每个红球 \(i\) 我们都连向中间四个点,边权分别为 \(x_i+y_i,x_i-y_i,-x_i+y_i,-x_i-y_i\);然后另一边的每个蓝球 \(i\) 我们也从中间四个点连到他,边权分别为 \(-x_i-y_i,-x_i+y_i,x_i-y_i,x_i+y_i\)。
那么这个问题就变成和 QOJ7185 几乎一样的形式了,只不过此时是中间有四个点,左右两侧各有 \(M\) 个点。类似地维护中间四个点 \(Q_1,Q_2,Q_3,Q_4\) 它们 \(Q_i\to Q_j\) 的最短路,然后再维护 \(s\to Q_i,Q_i\to t\) 的最短路即可。
时间复杂度:\(O(M\log M)\) 带很大常数。
[SD2024 一轮省集] Circuits - By alpha1022
二维平面上有 \(n+m\) 个点 \((x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\) 和 \((a_1,b_1),(a_2,b_2),\cdots,(a_m,b_m)\)。
现在所有的 \((x_i,y_i)\)(\(1\le i\le n\))已经按照 \(1,2,\cdots,n\) 的顺序连成一个环。现在你可以选择 \(k\) 个 \((a_j,b_j)\) 和环上的 \(k\) 条边,把你选的 \((a_j,b_j)\) 按照任意顺序分别插入到这 \(k\) 条边的中间。这里每条边里面至多插入一个 \((a_j,b_j)\),每个 \((a_j,b_j)\) 最多被选中一次。
在做完上述操作后会得到一个 \(n+k\) 个点的环,定义该方案的分数为所有边的两端点的曼哈顿距离之和。此外,如果选中了 \((a_j,b_j)\),分数还会额外加上 \(w_j\)。你希望最大化这个方案的分数。
你需要对 \(k=1,2,\cdots,n\) 求出上述问题的答案。
\(1\le n\le m\le 10^5,-10^8\le a_i,b_i,x_i,y_i,w_i\le 10^8\)。
考虑一个点 \((a_i,b_i)\) 和一条边匹配,权值为
\[|x_i-a_i|+|a_i-x_{(i\ \bmod\ n)+1}|+|y_i-b_i|+|b_i-y_{(i\ \bmod\ n)+1}|-|x_i-x_{(i\ \bmod\ n)+1}|-|y_i-y_{(i\ \bmod\ n)+1}| \]这里根据 \(a_i\) 和这两个 \(x\) 的大小关系,以及 \(b_i\) 和这两个 \(y\) 的大小关系,可以拆出来 \(3\times 3=9\) 个点。
接下来类似上题进行建图即可。复杂度 \(O((n+m)\log (n+m))\) 带很大常数。
[2022 ICPC 杭州区域赛] H. RPG Pro League
你在玩一个游戏,这个游戏中有三类角色:输出位,增益位,生存位。
一个队伍由四个角色构成,每个队伍必须形如:
- 两个输出位,一个增益位,一个生存位。
- 一个输出位,两个增益位,一个生存位。
现在有 \(n\) 个角色,第 \(i\) 个角色有一个可以担任的位置集合 \(S_i\subseteq\{输出,生存,增益\}\),让这个角色加入队伍的代价为 \(a_i\)。你希望组出最多的队伍数量,在此基础上求出最小的组队代价。一个角色只能加入至多一个队伍,且一个角色同时只能作为一个队伍中的一个位置。
有 \(q\) 次修改,每次给出 \(x,v\),表示将 \(a_x\leftarrow v\)。每次修改后你都需要求出上述问题的答案。
\(1\le n,q\le 10^5,1\le a_i\le 10^9\)。
解法一(官方做法)
考虑先算出最多能组多少队,然后再算出最小代价。把三种角色称为 A,B,C 类角色。
建一张图,左边有 \(4\) 个点分别代表 \(\{A\},\{B\},\{C\},\{A,B\}\),右侧七个点分别代表 \(A,B,C\) 的任意非空子集。右侧点 \(T\) 的点权就是所有 \(i\) 里面 \(S_i=T\) 的 \(i\) 的个数,对于左侧点 \(U\) 和右侧点 \(V\),如果 \(U\cap V\neq\varnothing\) 就连边。
现在相当于求这个二分图的多重最大匹配。
我们知道由 Hall 定理,存在 \(k\) 重完美匹配当且仅当 \(\forall S,|N(S)|\ge k|S|\)。于是答案就是
\[\min_{S}\left\lfloor\frac{|N(S)|}{|S|}\right\rfloor \]考虑如何算最小代价,按照权值从大到小依次考虑每个数,如果能删除他就删除。这里容易用贪心解释,也可以用拟阵来解释。那么修改的时候可能会删除一个数,插入一个数。类似人员调度那题进行维护即可。
解法二
还是考虑建那个图,只不过我们一开始就直接区分所有点。那么建出来的费用流图有三种边:
- \(s\to P_i\)(\(1\le i\le n\)),容量 \(1\) 边权 \(a_i\)。
- \(P_i\to Q_j\)(\(1\le j\le 4\)),容量 \(1\) 边权 \(0\)。
- \(Q_j\to t\)(\(1\le j\le 4\)),容量 \(ans\) 边权 \(0\)。
其中 \(ans\) 是我们求出来的答案。为了求这个答案,可以考虑每次依次把 \(Q_j\to t\) 的边一条一条增广,看能否增广成功。如果成功了,就把 \(ans\leftarrow ans+1\)。我们一直增广最短路就可以保证费用也是最小的。
现在还要修改 \(a_i\),怎么办?我们考虑此时如果 \(i\) 在匹配里,那么可能会增大 \(a_i\) 然后把他换成别的;如果 \(a\) 不在匹配里,那么可能会减小 \(a_i\) 然后把匹配里的一个点换成他。
如果把 \(i\) 换成了 \(j\),画一下增广路,发现形如 \(s\to i\to Q_x\to j\to s\)。也就是说我们只需要判断是否存在一个负环。这怎么看都是随便维护。
标签:10,le,2024.4,log,times,定能,cdots,般飞,考虑 From: https://www.cnblogs.com/YunQianQwQ/p/18164910