Kruskal重构树 学习笔记

我们回顾一下最小与最大生成树的性质：

对于一张图的最小生成树，原图中任意两个节点中任意一条路径的边权最大值的最小值为生成树中节点路径间边权的最大值。最大生成树则相反，原图中任意两个节点中任意一条路径的边权最小值的最大值为生成树中节点路径间边权的最小值。

以下以最小生成树为例，最大生成树则同理。

回顾一下 \(\text{Kruskal}\) 算法求最小生成树的过程：先将所有的边权排序，再通过并查集判断两个点是否已经在同一颗树上，若没有则相连。我们换一种建树方式：同样是先将所有的边权排序，也同样通过并查集判断，但在连边的时候，我们不是直接将两个点相连，而是新建一个节点连向这两个点在并查集中的祖先，且新节点的点权为原图两点的边权（此时这个新节点就不是原图中的节点了）。完毕后构成的一棵树即为原图的 \(\text{Kruskal}\) 重构树。\(\text{Kruskal}\) 重构树有以下性质：

1. 是一颗二叉树；
2. 若原本需要生成的是最小生成树，则重构树是一个大根堆，最大生成树则相反；
3. 原图中任意两点在重构树上的 \(\text{LCA}\) 的点权即为该两点在原图中经过的路径边权最大值的最小值，即在最小生成树中经过的路径边权最大值。这意味着对于一个权为 \(x\) 的节点，其子树中的任意两个节点都可以在原图（或最小生成树）中通过权都小于等于 \(x\) 的边到达。

结合图理解：

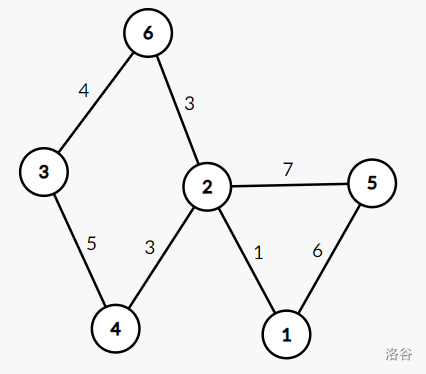
该图的最小生成树是：

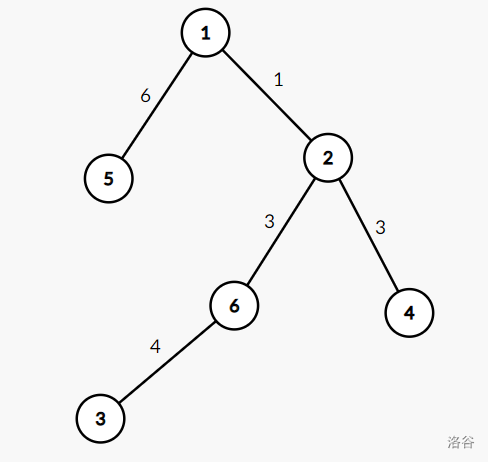
该图的 \(\text{Kruskal}\) 重构树是：

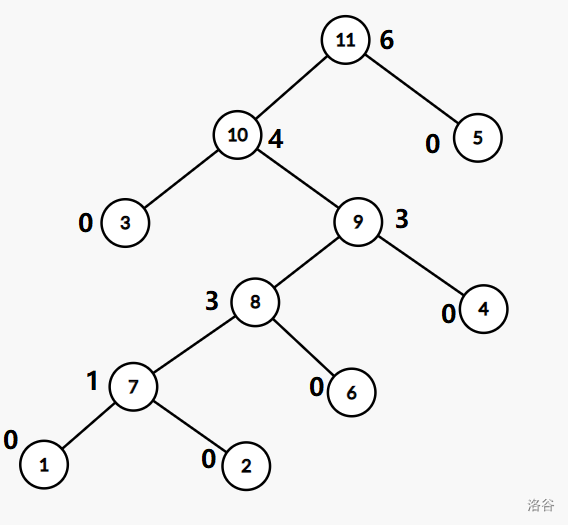
节点旁边的数值为该点的点权。\(\text{Kruskal}\) 重构树的结构有点类似于哈夫曼树。其叶节点都是原图中的节点，其余节点为求最小生成树时建立重构树所产生的新节点。善用 \(\text{Kruskal}\) 重构树的性质可以解决许多类型的题目。

例题：P4197 Peaks

题目大意：给定一张 \(n\) 个点、\(m\) 条边的无向图，点有点权，边有边权，有 \(q\) 个询问，每次询问对于一个节点，经过所有边权小于等于 \(x\) 的边所能到达的节点中第 \(k\) 高的点权，无解输出 \(-1\)。

思路：容易想到对原图建立 \(\text{Kruskal}\) 重构树。对于每一个节点，我们维护动态开点的权值线段树（需要离散化）记录其子树中的所有点权，到祖先时合并左右两节点的线段树到自身即可（易知重构树中的节点要么是叶节点，要么有两个子节点）。我们可以提前处理出倍增数组，对于每一个询问给出的点 \(u\) ，我们向上倍增，找到 \(u\) 的祖先中深度最浅的、点权小于等于 \(x\) 的节点，它的子树中的所有叶节点即为在原图中可以通过所有权都小于等于 \(x\) 的边所能到达的节点（由上面的性质可知）。找到这个节点后先判断无解，若有解再线段树上二分即可。由于是在线算法，所以也可以处理 P7834 [ONTAK2010] Peaks 加强版 中的强制在线操作。

P4197 AC Code:

#include <bits/stdc++.h>
#define mid (l + r >> 1)

using namespace std;

struct E {
    int u, v, w;
    
    const bool operator<(const E &rhs) const {
        return w < rhs.w;
    }
};

int n, m, u, v, w, gr, cnt, macnt = 1, tot, q, f[200005], fa[200005][20], h[100005], p[200005], b[100005], r[100005], rt[200005], sum[40000005], ls[40000005], rs[40000005];
E e[500005];
unordered_map<int, int> ma;

int fgr(int u, int x) {
    for (int i = 19; ~i && p[fa[u][0]] <= x; --i)
        if (p[fa[u][i]] <= x)
            u = fa[u][i];
    
    return u;
}

int find(int x) {
    return x == f[x]? x: f[x] = find(f[x]);
}

void merge(int l, int r, int &x, int y, int z) {
    if (!y) { x = z; return; }
    if (!z) { x = y; return; }
    
    sum[x = ++tot] = sum[y] + sum[z];
    
    if (l < r) {
        merge(l, mid, ls[x], ls[y], ls[z]);
        merge(mid + 1, r, rs[x], rs[y], rs[z]);
    }
}

void ExKruskal() {
    cnt = n;
    sort(e + 1, e + m + 1);
    
    for (int i = 1; i <= m; ++i)
        if ((u = find(e[i].u)) != (v = find(e[i].v))) {
            f[u] = f[v] = ++cnt;
            f[cnt] = cnt;
            p[cnt] = e[i].w;
            fa[u][0] = fa[v][0] = cnt;
            merge(1, macnt, rt[cnt], rt[u], rt[v]);
        }
}

void add(int l, int r, int &x, int tar) {
    x = ++tot;
    
    if (l == r) {
        ++sum[x];
        
        return;
    }
    
    if (tar <= mid) add(l, mid, ls[x], tar);
    else add(mid + 1, r, rs[x], tar);
    
    sum[x] = sum[ls[x]] + sum[rs[x]];
}

int query(int l, int r, int x, int k) {
    if (l == r) return l;
    
    if (sum[ls[x]] >= k)
        return query(l, mid, ls[x], k);
    else
        return query(mid + 1, r, rs[x], k - sum[ls[x]]);
}

int main() {
    p[0] = 2e9;
    scanf("%d %d %d", &n, &m, &q);
    
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &h[i]);
        f[i] = i, b[i] = h[i];
    }
    
    sort(b + 1, b + n + 1);
    r[1] = b[1];
    ma[b[1]] = 1;
    
    for (int i = 2; i <= n; ++i)
        if (b[i] != b[i - 1]) {
            r[++macnt] = b[i];
            ma[b[i]] = macnt;
        }
    
    for (int i = 1; i <= n; ++i)
        add(1, macnt, rt[i], ma[h[i]]);
    
    for (int i = 1; i <= m; ++i) {
        scanf("%d %d %d", &u, &v, &w);
        e[i].u = u, e[i].v = v, e[i].w = w;
    }
    
    ExKruskal();
    
    for (int i = 1; i < 20; ++i)
        for (int j = 1; j <= cnt; ++j)
            fa[j][i] = fa[fa[j][i - 1]][i - 1];
    
    while (q--) {
        scanf("%d %d %d", &u, &v, &w);
        gr = fgr(u, v);
        
        if (sum[rt[gr]] < w)
            puts("-1");
        else
            printf("%d\n", r[query(1, macnt, rt[gr], sum[rt[gr]] - w + 1)]);
    }
    
    return 0;
}