深度学习模型通常堆叠大量结构和功能相同的结构,虽然有效,但会导致参数数量大幅增加,给实际应用带来了挑战。为了缓解这个问题,
LORS(低秩残差结构)允许堆叠模块共享大部分参数,每个模块仅需要少量的唯一参数即可匹配甚至超过全量参数的性能。实验结果表明,LORS减少解码器 70% 的参数后仍可达到与原始模型相当甚至更好的性能来源:晓飞的算法工程笔记 公众号
论文: LORS: Low-rank Residual Structure for Parameter-Efficient Network Stacking

Introduction
在当前大模型繁荣的时代,一个普遍的问题是参数量大幅增加,这给训练、推理和部署带来了挑战。目前有各种方法来减少模型中的参数数量,例如知识蒸馏,将大型模型压缩为较小的模型,同时试图保持其性能,但仍可能导致模型容量的下降;剪枝,从模型中删除冗余参数,但会影响模型的稳定性;量化,降低模型参数的数值精度,降低存储和计算量,但可能会导致模型精度损失;参数共享,通过在不同层之间共享参数来减少参数数量,但可能会限制模型的表达能力。
与上述方法不同,论文观察到一个导致参数数量庞大的重要事实:层堆叠在神经网络中的广泛使用。层堆叠是指那些具有相同架构并执行相同或相似功能的模块,但由于随机初始化和训练更新而具有不同的参数。堆叠的例子可以在许多著名的神经网络中找到,比如经典的ResNet模型和Transformers。特别是,Transformers严重依赖堆栈结构,并且通常在编码器和解码器中采用完全相同的多层堆栈。现在它已成为计算机视觉、自然语言处理等领域许多优秀模型不可或缺的组成部分。
尽管层堆叠对于增强模型容量非常有效,但也会导致参数数量的急剧增加。例如,GPT-3使用 1750 亿个参数,由 96 个堆叠的Transformer层组成。如何才能享受堆栈带来的好处,同时减少所需的参数数量?论文注意到堆叠的解码器具有相同的结构和相似的功能,这表明它们的参数之间应该存在一些共性。然而,由于它们处理不同的输入和输出分布,因此它们的参数也必须有独特的方面。因此,一个自然的想法是:也许可以用共享参数来表示共享方面,同时允许每个堆叠模块仅保留捕获其独特特征的参数,从而减少总体参数使用。
基于上述考虑,论文建议将堆叠模块的参数分解为两部分:代表共性的共享参数和捕获特定特征的私有参数。共享参数可供所有模块使用并共同训练,而私有参数则由每个模块单独拥有,在保持模型性能的同时减少参数量。为了实现这一目标,受LoRA方法的启发,论文引入了低秩残差结构 (LORS) 的概念,本质上是将私有参数添加到共享参数中,就像残差连接将残差信息添加到特征中一样。
为了验证论文的想法,选择AdaMixer(一个强大的基于查询的对象检测器)作为实验对象。其堆叠的解码器中包含大量自适应和静态参数,是展示LORS有效性的理想候选者。自适应参数和静态参数的区别在于是否随着不同的输入而变化,而论文的目标是证明LORS可以有效减少两类参数的总体使用,同时保持模型的性能。对此检测器进行的广泛实验表明,LORS成功地减少了AdaMixer解码器中高达 70% 的参数,同时能够实现与其普通版本相当甚至更优越的性能。
总之,论文的贡献可以总结为:
- 论文提出了用于堆叠网络的新颖低秩残差结构
LORS,与普通结构相比,在大幅减少参数数量的同时保持甚至提高性能。 - 论文引入有效的方法来减少堆叠结构中的静态参数和自适应生成参数,这使得论文提出的
LORS更加通用。 - 论文的方法有潜力作为大型模型的基本网络结构之一,这些模型受到堆叠网络导致的参数过多问题的影响很大。
LORS能使参数更加高效,从而在实际应用中更容易实现。
Approach
Preliminary
-
The mechanism of LoRA
低秩适应(LoRA)技术是一种新颖的方法,使大型预训练语言模型能够适应特定任务。LoRA的关键思想是引入一个低秩参数矩阵,该矩阵能够捕获任务相关的知识,同时保持原始预训练参数固定。
从数学角度来看,给定一个预训练的参数矩阵 \(W\in \mathbb{R}^{d\times h}\),LoRA使用低秩矩阵 \(B\in\mathbb{R}^{d\times r}\) 和投影矩阵 \(A\in\mathbb{R}^{r\times h}\) 来适应 \(W\) ,其中秩 \(r\ll d,h\)。适应的参数矩阵由以下计算:
其中\(BA\) 用于捕获特定于任务的知识。
LoRA的主要优势在于显着减少需要微调的参数量,从而降低计算成本以及内存需求。在某些情况下,即使个位数值的秩 \(r\) 也足以将模型微调到所需状态,比直接训练 \(W\) 中的参数的开销少数十倍。此外,通过固定原始参数,LoRA避免了灾难性遗忘,这是微调大型模型时的常见问题。
-
Query-based object detection
在对象检测领域,基于查询的检测器建立了一种新的范例,利用一组可学习的查询向量与图像特征图进行交互:
\[Q_{\mathrm{updated}}=\mathrm{Atention}(Q,K(V)) \quad\quad(2) \]其中 \(Q\)、\(K\) 和 \(V\) 表示查询、键和值。可学习查询 \(Q\) 最终用于预测对象类和边界框,而 \(K\) 和 \({\cal{V}}\) 通常为编码的图像特征。经过连续的解码层,\(Q\) 不断地与 \(K\) 和 \(V\) 交互来细化是一种常见的做法,而这些层通常由结构相同的解码器组成。
-
Decoders of AdaMixer
AdaMixer是一种基于查询的检测器,添加自适应通道混合(ACM)和自适应空间混合(ASM)方法,大大增强了性能。
给定一个采样特征 \({\textbf{x}}\in\ \mathbb{R}^{P_{\mathrm{in}}\times C}\),其中 \(\textstyle C\ = d_{feat/g}\),\(g\) 为采样组数。采样特征通过组采样操作获得的,该操作将每个多尺度特征的空间通道 \(d_{feat}\) 划分为 \(g\) 组,然后对每个组内特征进行单独3D采样操作,得到的多组采样特征分别进行后续的ACM和ASM操作。
首先对采样特征执行ACM(自适应通道混合)操作,根据对象查询 \(\mathbf{q}\) 生成的自适应权重在通道维度转换特征 \(\mathbf{x}\),增强通道语义:
随后对通道增强的采样特征执行ASM(自适应空间混合)操作,通过对空间维度应用自适应变换,使得对象查询 \(\mathbf{q}\) 能够适应采样特征的空间结构:
ACM和ASM都为每个采样组训练独立的参数,最后整合多组输出将形状为 \(\mathbb{R}^{g\times C\times P_{out}}\) 的合并输出展平并通过线性层 \(L_{\mathrm{output}}\) 输出转换为 \(d_{q}\)维度,添加到原对象查询中。
与解码器的其他操作相比,ACM、ASM和输出线性变换 \(L_{\mathrm{output}}\) 拥有更多的参数,是模型参数量的主要贡献者。因此,论文选择它们作为目标组件来验证LORS方法在参数减少方面的有效性。
Formulation of Our Method
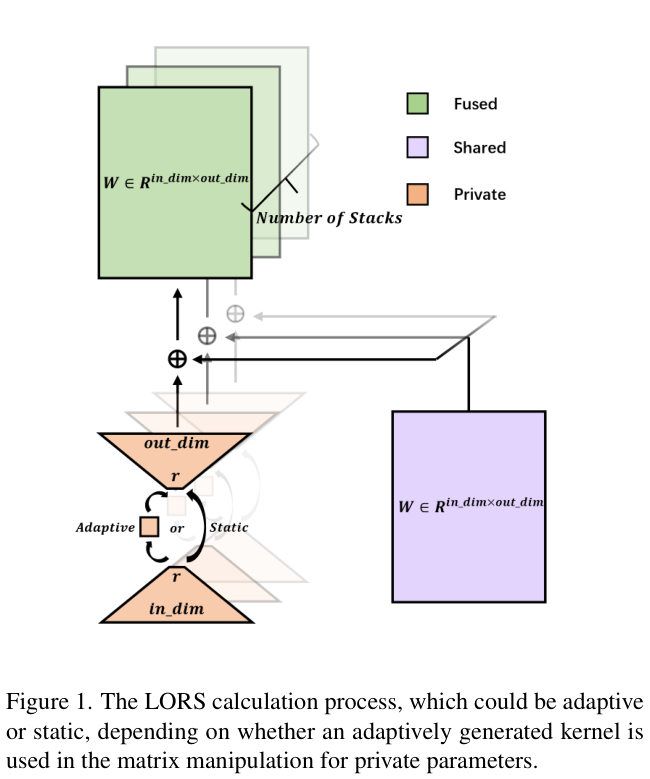
LORS的完整计算过程如图 1 所示,分为两种类型:自适应计算和静态计算。其中,“自适应”表示变换矩阵是否依赖于对象查询。
-
Static Low Rank Residual Structure (\(\mathrm{LORS}^\mathrm{T}\))
假设单个模块包含 \(N\) 个具有相同架构的堆叠层,并且 \(W_{i}\in\mathbb{R}^{d\times h}\) 是第 \(i\) 层的参数矩阵,则有:
\[W_{i}=W^{\mathrm{shared}}+W_{i}^{\mathrm{private}} \quad\quad(7) \]\(W^{\mathrm{shared}}\) 为所有堆叠层的共享参数,\(W_{i}^{\mathrm{private}}\) 为第 \(i\) 层的私有参数,其计算如下:
\[W_{i}^{\mathrm{private}} = {{{\sum_{k=1}^{K}B_{i k}A_{i k}}}} \quad\quad(8) \]\(B_{ik}\in\mathbb{R}^{d\times r}\),\(A_{ik}\in\mathbb{R}^{r\times h}\),其中秩 \(r\ll d\)。\(K\) 为用于计算\(W_{i}^{\mathrm{private}}\) 的参数组的数量。

\(\mathrm{LORS}^\mathrm{T}\) 计算 \(W_{i}^{\mathrm{private}}\) 的伪代码如图 2 所示。
-
Adaptive Low Rank Residual Structure (\(\mathrm{LORS}^\mathrm{A}\))
定义 \(\hat{W}_i\in\mathbb{R}^{d\times h}\) 为第 \(i\) 个堆叠层中自适应生成参数,其计算为:
\[\hat{W}_{i}=\hat{W}^{\mathrm{shared}}+\hat{W}_{i}^{\mathrm{private}} \quad\quad(9) \]其中跨层共享参数 \(\hat{W}^{\mathrm{shared}}\in\mathbb{R}^{d\times h}\) 和层私有参数 \({\hat{W}}_{i}^{\mathrm{private}}\in\mathbb{R}^{d\times h}\)都是基于查询 \(q\) 计算得到的:
\[\begin{array}{l} {{\hat{W}_{i}^{\mathrm{shared}}=\mathrm{Linear(q)}\in\mathbb{R}^{d\times h}}} \quad\quad(10) \\ {{\hat{W}_{i}^{\mathrm{private}}=\sum_{k=1}^{K}\hat{B}_{i k}\hat{E}_{i k}\hat{A}_{i k}}} \quad\quad\ \ (11) \\ {{\hat{E}_{i k}=\mathrm{Linear(q)}\in\mathbb{R}^{r\times r}}} \quad\quad\quad\quad(12) \end{array} \]其中 \(\hat{B}_{i k}\ \in\ \mathbb{R}^{d\times r}\),\({\hat{A}}_{ik}\in\mathbb{R}^{r\times h}\),秩 \(r\ll d,h\)。

\(\mathrm{LORS}^\mathrm{A}\) 计算 \({\hat{W}}_{i}^{\mathrm{Private}}\) 的伪代码如图 3 所示。
Applying LORS to AdaMixer’s Decoders
将LORS应用到AdaMixer的每个解码器的ACM、ASM和 \(L_{\mathrm{output}}\) 的线性变换的参数中。
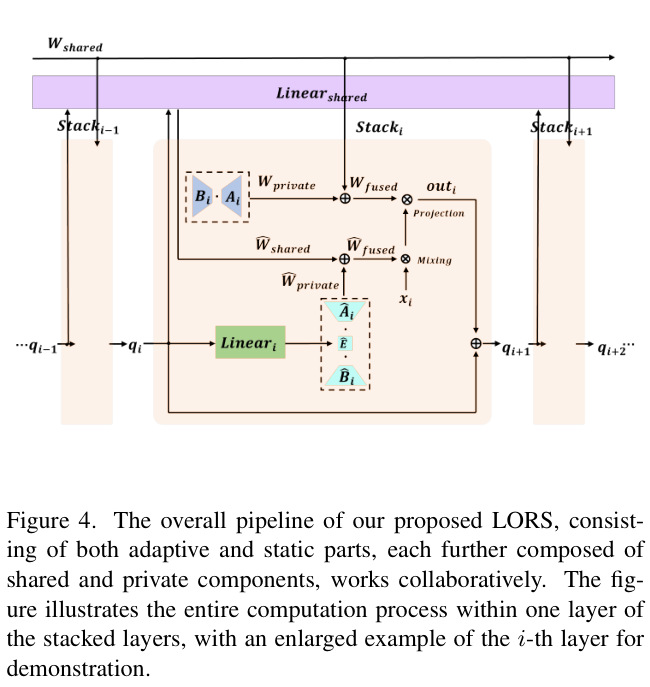
AdaMixer中运行的LORS的整体流程如图 4 所示。对于每组采样点,\(\mathrm{LORS}^\mathrm{A}\) 用于减少ACM的 \({M}_{c}\)(映射 \(\mathbb{R}^{d_q}\) 到 \(\mathbb{R}^{C\times C}\))和ASM的 \(M_{s}\) 的参数(映射 \(\mathbb{R}^{d_q}\) 到 \(\mathbb{R}^{P_{in}\times P_{out}}\),而 \(\mathrm{LORS}^\mathrm{T}\) 则用于最小化 \(L_{\mathrm{output}}\) 中的参数(映射 \(\mathbb{R}^{C\times P_{\mathrm{out}}}\) 到 \(\mathbb{R}^{d_q}\) )。
从上面括号中的映射关系可以看出,\(M_{c}\)、\(M_{s}\)、\(L_{\mathrm{output}}\) 的参数量分别为 \(d_q\times C\times C\)、\(d_{q}\times P_{\mathrm{in}}\times P_{\mathrm{out}}\)、\(d_{q}\times C\times P_{\mathrm{out}}\)。当分组采样策略由 2 组、每组 64 点组成时,变量的值为 \(d_{q}=256\)、\(C= 64\)、\(P_{\mathrm{in}}=64\) 和 \(P_{\mathrm{out}}=128\),进而计算出 \(M_{c}\)、\(M_{s}\) 和 \(L_{\mathrm{output}}\) 的参数数量均超过百万。
事实上,这三个组件共同占据了以ResNet-50为主干的AdaMixer模型总参数的大部分,同时它们也是增强模型性能的主要驱动力。综上,这也就是论文对它们进行LORS实验的动机。
Analysis on Parameter Reduction
定义 \(W\in \mathbb{R}^{d\times h}\) 为堆叠结构中每层都存在的权重参数,\(N\) 为堆叠层数:
- 如果是静态的,则原本就有 \(d\times h\) 个参数,而使用 \(\mathrm{LORS}^\mathrm{T}\) 后平均每层仅需要 \(\frac{1}{N}\times d\times h + K\times(d\times r+r\times h)\)个参数。
- 如果是自适应的,通过 \(q\) 线性变换生成需要 \(d_{q}\times d\times h\) 个参数,其中 \(d_{q}\) 是 \(q\) 的维度,使用 \(\mathrm{LORS}^\mathrm{A}\) 每层平均仅需要 \(\frac{1}{N}\times d_q\times d\times h + K\times(d_q\times r^2 + d\times r + r\times h)\) 个参数。
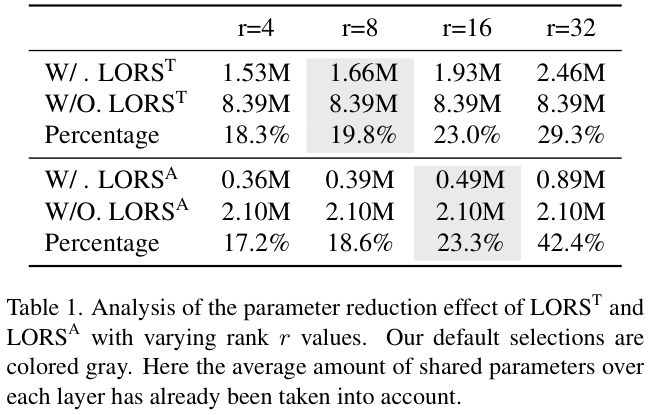
为了更直观地展示LORS的参数减少效果,在ASM设置 \(d_{q}=256\),\(d=64\),\(h=128\),\(K=2\),\(h=256\),\(L_{\mathrm{output}}\) 设置 \(d=2\times 128\times 128\),\(K\,=\,1\) 的情况下,\(\mathrm{LORS}^\mathrm{T}\) 和 \(\mathrm{LORS}^\mathrm{A}\) 对不同 \(r\) 值的参数减少情况如表 1 所示。
Experiments
Implementation Details
-
Training.
使用权重衰减为 0.0001 的AdamW优化器,在 8 个Nvidia V100 GPU上训练所有模型,批量大小为 16,学习率为 2.5 × e−5。模型训练 12 或 36 个 周期,对于 12 周期训练,学习率在第 8 和 11 周期下降 10 倍;对于 36 周期训练,在第 24 和 33 周期学习率下降 10 倍。
低秩值方面,\(\mathrm{LORS}^\mathrm{A}\) 设置为 \(r=16\),\(\mathrm{LORS}^\mathrm{T}\) 设置为 \(r=8\)。
所有实验中,\(\mathrm{LORS}^\mathrm{A}\) 的参数组数量设置为\(K\,=\,[1,1,2,2,3,3]\),应用于AdaMixer解码器中的ACM和ASM,而\(L_{\mathrm{output}}\)则设置为 \(K\ =\ [1,1,1,1,1,1]\)。
组采用时将特征通道分为 2 组,每组 64 个采样点,而不是AdaMixer默认的 4 组,每组 32 个采样点,旨在增加LORS的参数可压缩空间。根据AdaMixer论文和论文的实验,这并不会简介提高性能。
主干网络使用ImageNet-1k预训练模型进行初始化,LORS参数初始化如下面所示,其余参数则由Xavier初始化。关于模型训练的所有其他方面,如数据增强、损失函数等,只需遵循AdaMixer的设置即可。
-
Initialization Strategies
论文对LORS中的各个组件尝试了多种初始化方法,确定了整体的初始化方法如下:
- \(\mathrm{LORS}^\mathrm{T}\):对于静态
LORS,对 \(W^\mathrm{shared}\) 和每个 \({\boldsymbol{B}}\) 采用Kaiming初始化,并对每个 \(A\) 进行零初始化。 - \(\mathrm{LORS}^\mathrm{A}\):对于自适应
LORS,将Kaiming初始化每个 \(\tilde{W}^\mathrm{shared}\)、\({\hat{B}}\) 和 \({\hat{A}}\)线性变换权重。此外,论文对每个 \({\hat{E}}\) 的线性变换权重使用零初始化
Main Results
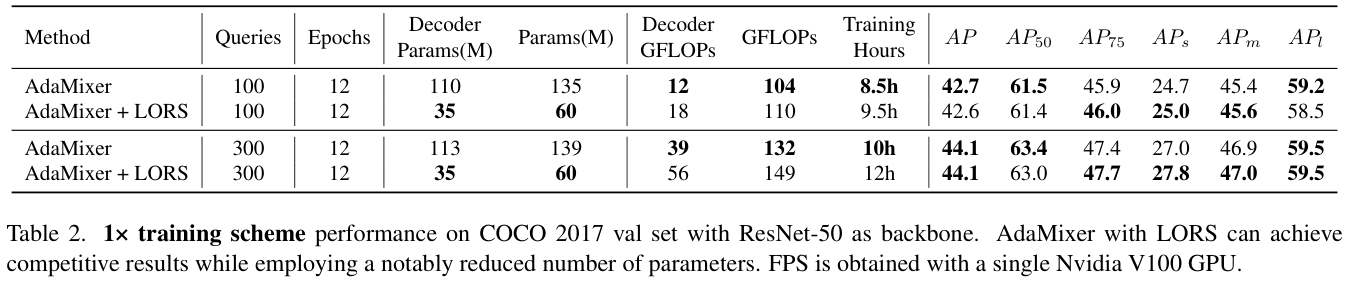
表 2 展示了在 1× 训练方案下使用和不使用LORS技术的性能比较。
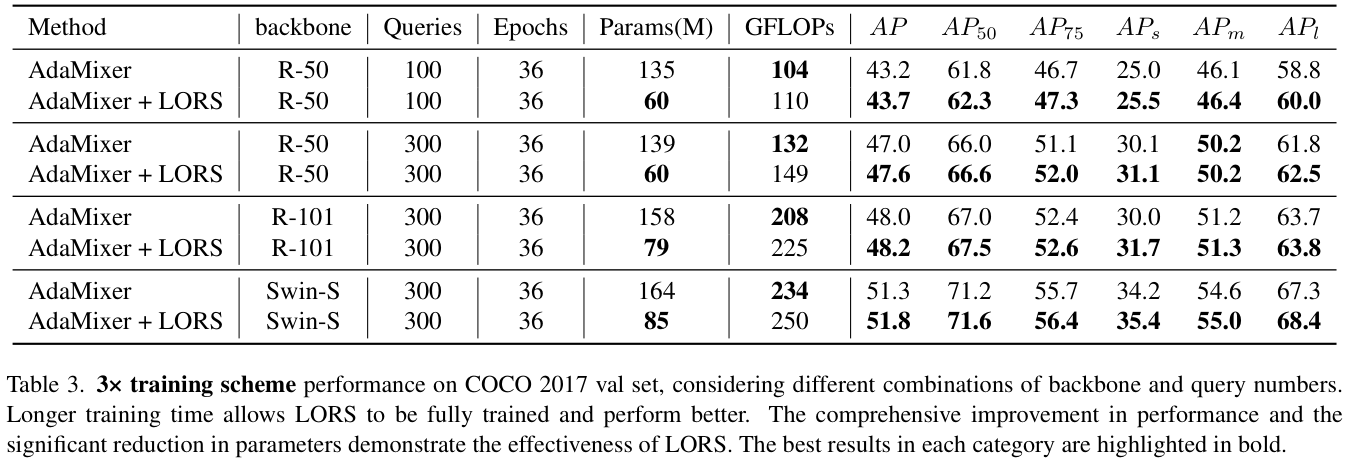
表 3 展示了AdaMixer+LORS方法在不同骨干网和查询数的3×训练方案下的性能。
Ablation Study

表 4 展示了 \(\mathrm{LORS}^\mathrm{A}\) 和 \(\mathrm{LORS}^\mathrm{T}\) 对模型参数和性能的影响进行消融研究

表 5 对比了共享权重和私有权重中哪一个对解码器的性能影响更大。
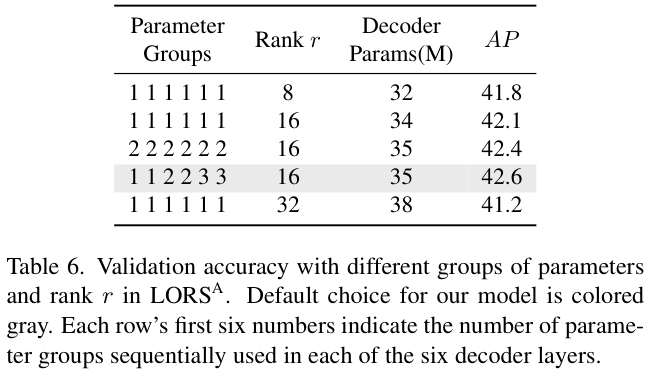
表 6 探索了自适应LORS的最佳参数组数量和秩 \(r\) 的值。
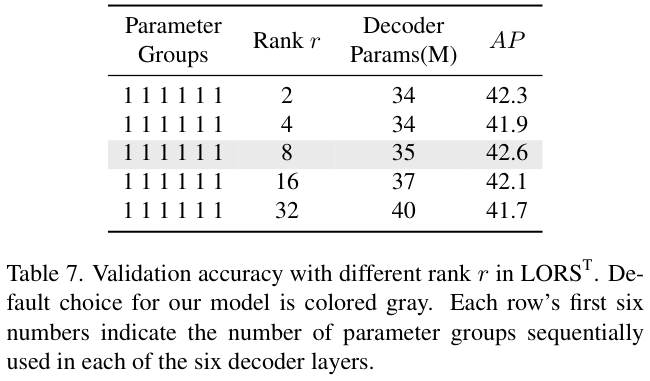
表 7 研究了 \(\mathrm{LORS}^\mathrm{T}\) 的最佳配置设置。
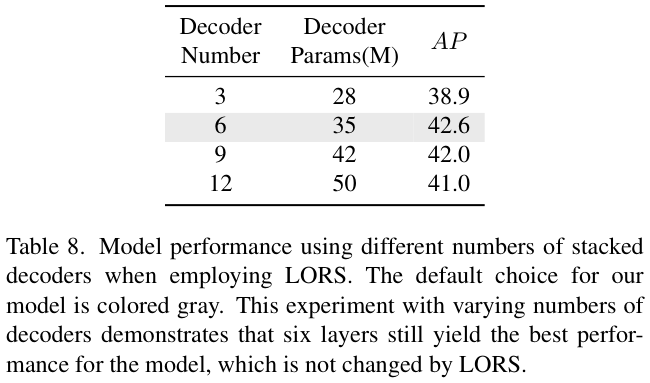
表 8 对结合LORS结构的最佳解码器层数进行实验对比。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
