桥

定义：删除后会增加联通块数量的边被称作桥。

那么，如何求解呢？

方法一

首先跑出一颗dfs树。比如下图（\(2-6,1-5\) 的边是非树边）：

可以发现，所有非树边和其构成的环上的所有边不可能是桥，因为删去后仍可以通过环的另一半。比如上图中只有 \(1-2\) 一个桥。那是不是除了这些边以外都是桥呢？很明显是的，因为只存在这一条边连接它的子树和父亲子树。

所以我们可以找出所有非树边，然后求出它两个端点的 LCA，再使用树上差分求解。

但这样还是太麻烦了，所以我们可以用到dfs树的一个性质：所有非树边的两个端点在树上一定有祖先关系。这样我们就不用写 LCA 了。

时空复杂度均为 \(O(N+M)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001, MAXM = MAXN;

int n, m, dep[MAXN], s[MAXN];
vector<pii> e[MAXN];
vector<int> ans;

void dfs(int u, int f) {
  for(auto [v, id] : e[u]) {
    if(!dep[v]) {
      dep[v] = dep[u] + 1;
      dfs(v, id);
      s[u] += s[v];
    }else if(dep[v] < dep[u] && f != id) {
      s[u]++, s[v]--;
    }
  }
  if(f && !s[u]) {
    ans.push_back(f);
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back({v, i});
    e[v].push_back({u, i});
  }
  for(int i = 1; i <= n; ++i) {
    if(!dep[i]) {
      dep[i] = 1;
      dfs(i, 0);
    }
  }
  cout << ans.size() << "\n";
  for(int x : ans) {
    cout << x << " ";
  }
  return 0;
}

方法二

同样的，先跑出一颗dfs树。

我们令 \(dfn_u\) 表示 \(u\) 的时间戳，\(low_u\) 为 \(u\) 的子树内所有节点中，仅通过非树边能够抵达的结点之中的 \(\min \{dfn_v\}\)。

设树上结点 \(u\) 的父亲是 \(v\)，如果 \(low_u\) 大于 \(dfn_v\)，说明不存在 \(u\) 的子树到 \(u\) 的祖先的非树边，则这条边就是桥。

时空复杂度均为 \(O(N+M)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001, MAXM = MAXN;

int n, m, dfn[MAXN], low[MAXN], tot;
vector<pii> e[MAXN];
vector<int> ans;

void dfs(int u, int f) {
  dfn[u] = low[u] = ++tot;
  for(auto [v, id] : e[u]) {
    if(!dfn[v]) {
      dfs(v, id);
      low[u] = min(low[u], low[v]);
    }else if(dfn[v] < dfn[u] && f != id) {
      low[u] = min(low[u], dfn[v]);
    }
  }
  if(f && dfn[u] == low[u]) {
    ans.push_back(f);
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back({v, i});
    e[v].push_back({u, i});
  }
  dfs(1, 0);
  cout << ans.size() << "\n";
  for(int x : ans) {
    cout << x << " ";
  }
  return 0;
}

割点

定义：删除后会增加联通块数量的点被称作割点。

用同样的方式思考：先跑出一颗dfs树，比如下图。

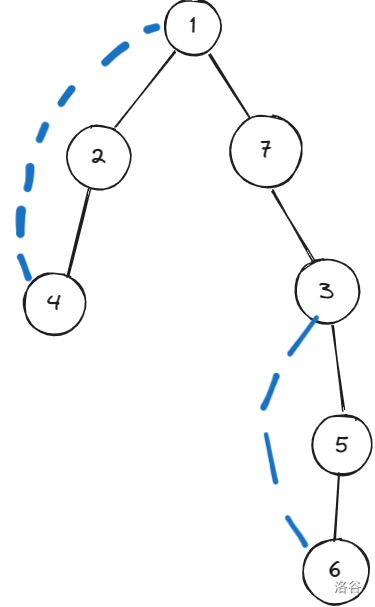
这张图中只有 \(7\) 是割点。

可以想到，如果一个点 \(u\) 不为根节点，且它的所有儿子至少有一个没有通往 \(u\) 的祖先的非树边，即 \(dfn_u > low_v\)，则代表删除 \(u\) 后该儿子会独立，即 \(u\) 是割点。

时空复杂度均为 \(O(N+M)\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 200001, MAXM = MAXN;

int n, m, dfn[MAXN], low[MAXN], tot;
vector<int> e[MAXN], ans;

void dfs(int u, int fa) {
  dfn[u] = low[u] = ++tot;
  int cnt = 0;
  bool op = 1;
  for(int v : e[u]) {
    if(v != fa) {
      if(!dfn[v]) {
        cnt++;
        dfs(v, u);
        op &= (low[v] < dfn[u]);
        low[u] = min(low[u], low[v]);
      }else if(dfn[v] < dfn[u]) {
        low[u] = min(low[u], dfn[v]);
      }
    }
  }
  if((!fa && cnt > 1) || (fa && !op)) {
    ans.push_back(u);
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
    e[v].push_back(u);
  }
  for(int i = 1; i <= n; ++i) {
    if(!dfn[i]) {
      dfs(i, 0);
    }
  }
  sort(ans.begin(), ans.end());
  cout << ans.size() << "\n";
  for(int x : ans) {
    cout << x << " ";
  }
  return 0;
}

边双连通分量

定义：一个任意两个结点 \(u,v\) 均可在删除任意一条边后仍然可以互相到达的极大子图被称为边双连通分量，即没有桥的极大子图。

方法很简单，只需把所有桥删去后看有多少个联通块即可

时空复杂度均为 \(O(N+M)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001, MAXM = 200001;

int n, m, dfn[MAXN], low[MAXN], tot, cnt, top;
bool flag[MAXM], vis[MAXN];
vector<pii> e[MAXN];
vector<int> ans[MAXN];

void dfs(int u, int f) {
  dfn[u] = low[u] = ++tot;
  for(auto [v, id] : e[u]) {
    if(!dfn[v]) {
      dfs(v, id);
      low[u] = min(low[u], low[v]);
    }else if(dfn[v] < dfn[u] && f != id) {
      low[u] = min(low[u], dfn[v]);
    }
  }
  if(f && dfn[u] == low[u]) {
    flag[f] = 1;
  }
}

void DFS(int u) {
  if(vis[u]) {
    return;
  }
  vis[u] = 1;
  ans[top].push_back(u);
  for(auto [v, id] : e[u]) {
    if(!flag[id]) {
      DFS(v);
    }
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back({v, i});
    e[v].push_back({u, i});
  }
  for(int i = 1; i <= n; ++i) {
    if(!dfn[i]) {
      dfs(i, 0);
    }
  }
  for(int i = 1; i <= n; ++i) {
    if(!vis[i]) {
      top++;
      DFS(i);
    }
  }
  cout << top << "\n";
  for(int i = 1; i <= top; ++i) {
    cout << ans[i].size() << " ";
    for(int x : ans[i]) {
      cout << x << " \n"[x == ans[i].back()];
    }
  }
  return 0;
}