by TheBigYellowDuck
一些没有做整场或者不值得写比赛记录的杂题。
[ABL D] Flat Subsequence
子序列问题,容易想到跟最长上升子序列类似的 dp 方法。
设 \(f(i)\) 为以 \(i\) 结尾的合法序列的最大长度。转移方程为
\[f(i)=\max\limits_{j<i}\{f(j)\}+1 \]其中 \(j\) 要满足 \(|a_j-a_i|\leq k\)。
朴素转移时间复杂度 \(\mathcal{O}(n^2)\),考虑优化。转移方程已经很简洁,考虑对 \(j\) 的范围下手。
注意到 \(a_i-k\leq a_j\leq a_i+k\),转移方程可以被写为一个区间最值的形式。
\[f(i)=\max\limits_{a_i-k\leq a_j\leq a_i+k}\{f(j)\}+1 \]考虑线段树优化。我们在 \(a_i\) 的位置上记录 \(f(i)\) 的值,这样可以直接查询 \(f(j)\) 的最小值。
时间复杂度优化到 \(\mathcal{O}(n\log n)\)。
[ABL E] Replace Digits
开一棵线段树维护每一位上的数字。建树的时候叶子节点的初始值设为它的位值,从叶子向上统计答案相当于用位值原理展开了每一位。
区间推平相当于把一段区间的和变为 \(i\times 111\cdots 11000\cdots 0\),考虑倒着预处理 \(10^i\) 的前缀和数组。
令 $$\displaystyle pre_i=\sum_{j=1}^i 10^{n-j}$$则将 \([l,r]\) 推平为 \(x\) 只需要将这一段的和赋值为 \(x\times (pre_r-pre_{l-1})\) 即可。
时间复杂度 \(\mathcal{O}((n+q)\log n)\)。
[ABC221D] Online games
一眼典题,直接差分数组上修改再前缀和还原序列即可。
但是数据范围不允许差分,怎么办?
我们把差分过程转移到 \(\text{map}\) 上来做。维护当前的前缀和 \(sum\),对于每一个被修改过的点 \(x\),设上一个被修改过的点为 \(y\),则 \([y,x-1]\) 的所有数都是 \(sum\),直接统计入答案即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。
[ABC247E] Max Min
考虑把所有数分成五类:
- \(a_i=X\)
- \(a_i=Y\)
- \(a_i>X\)
- \(a_i<Y\)
- \(X<a_i<Y\)
在一个区间内,不能出现第三类和第四类数,第五类没有影响,第一类和第二类至少都有一个。
设 \(f(i)\) 为以 \(i\) 结尾的合法子段数量。维护四个指针 \(p_1,p_2,p_3,p_4\) 记录 \([1,i]\) 中前四类数的最靠后的出现位置。
考虑计算 \(f(i)\),发现 \([1,\max\{p_3,p_4\}]\) 是不可以选的,\([\max\{p_3,p_4\}+1,\min\{p_1,p_2\}-1]\) 是可选可不选的,\([\min\{p_1,p_2\},i]\) 是必选的,从而 \(f(i)=\min\{p_1,p_2\}-\max\{p_3,p_4\}\)。
注意如果出现 \(\min\{p_1,p_2\}<\max\{p_3,p_4\}\) 的情况,那么 \(f(i)=0\)。
整个序列扫一遍,不断更新指针统计答案即可。
时间复杂度 \(\mathcal{O}(n)\)。
ABC251E Takahashi and Animals
环形 dp。设 \(f(i,0/1)\) 为考虑前 \(i\) 只动物,且否/是花费 \(a_{i-1}\) 选了 \(i-1\) 和 \(i\) 的连边的最小值。
考虑 \(f(i,0)\)。此时没选 \(a_{i-1}\),故 \(i-1\) 的食物只能来源于 \(a_{i-2}\),转移方程为
\[f(i,0)=f(i-1,1) \]考虑 \(f(i,1)\)。此时 \(i-1\) 已经有了食物,故 \(a_{i-2}\) 可选可不选,转移方程为
\[f(i,1)=\min\{f(i-1,0), f(i-1,1)\}+a_{i-1} \]考虑环的处理。可以手动枚举是否选择 \(a_n\) 分别 dp。
若选择 \(a_n\),则初始化 \(f(1,0)=+\infty\),\(f(1,1)=a_n\)。否则初始化 \(f(1,0)=0\),\(f(1,1)=+\infty\)。
时间复杂度 \(\mathcal{O}(n)\)。
ABC049D Connectivity
一个非常朴素的想法:直接用并查集维护两种道路的连通性。如果两个点最后在两种道路下所在集合都一样,则这两个点会互相做出贡献。
不能开二维数组统计 \((S_1,S_2)\) 的答案,那就把 \((S_1,S_2)\) 记录成数对塞进 \(\text{map}\) 里统计答案。
时间复杂度 \(\mathcal{O}(n\alpha(n))\)。
ABC233G Strongest Takahashi
被联考老哥挖出来的多倍经验(
覆盖一个 \(H\times H\) 的正方形严格强于覆盖一个 \(W\times H\) 的矩形,\(W\leq H\)。不妨只考虑用 \(W\times H\) 的矩形覆盖,付出 \(\max\{W,H\}\) 的代价。那就变成了 CF1198D。
设 \(f(a,b,c,d)\) 为覆盖以 \((a,b)\) 为左下角 \((c,d)\) 为右上角的矩形的最小代价。暴力枚举分界线转移。
时间复杂度 \(\mathcal{O}(n^5)\)。
ABC229F Make Bipartite
二分图先想到染色。不妨钦定 \(0\) 染了白色,设 \(f(i,j,k)\) 为考虑了前 \(i\) 个点,第 \(i\) 个点染了颜色 \(j\),第 \(1\) 个点染了颜色 \(k\) 的最小代价。\(j,k\in\{0,1\}\)。
通过枚举颜色转移。每条异色边都要被保留,同色边都要被删去。注意如果 \(j=0\) 就要删去 \((i,0)\) 这条边。最后讨论 \(j\) 是否等于 \(k\) 判断是否要保留 \((n,1)\)。
时间复杂度 \(\mathcal{O}(n)\)。
ABC190E Magical Ornament
在每一组 \((a,b)\) 之间连边,会得到一张图。要找的是一条包含给定顶点集合的最短路径。
注意到 \(k\leq 17\),考虑状压这一维。设 \(f(i,S)\) 表示以 \(c_i\) 结尾且包含的点集为 \(S\) 的最短路径。考虑预处理 \(c_i,c_j\) 之间的最短路,这样就可以 \(\mathcal{O}(1)\) 加点转移了。
时间复杂度 \(\mathcal{O}(k^22^k+(n+m)k)\)。
ABC196E Filters
考虑复合 \(n\) 次之后的函数图像,大概长成这个样子。
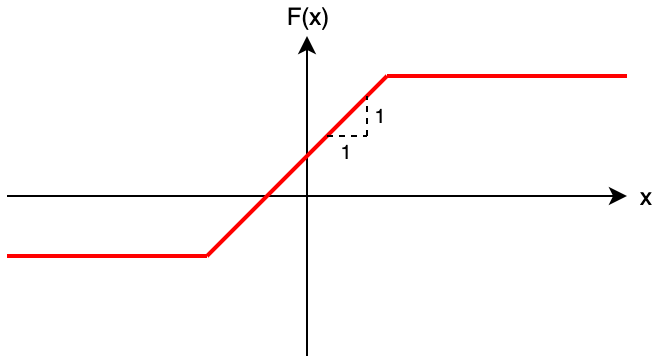
这个函数告诉我们,答案就是 \(\min\{c,\max\{x+a,b\}\}\) 的样子。
现在我们考虑计算 \(a,b,c\) 的值。会发现操作一就是对函数进行平移,而后两种操作就是分别给函数推平一个上下界。维护上下界 \(l,r\) 和平移增量 \(a\),答案就是 \(\min\{r,\max\{x+a,l\}\}\)。
时间复杂度 \(\mathcal{O}(n+q)\)。
ARC075E Meaningful Mean
考虑先让每个 \(a_i\) 都减去 \(k\),这样就只需要求多少个区间之和 \(\geq 0\)。
再做一遍前缀和,对于每个 \(i\) 分别求有多少个 \(j<i\) 满足 \(S_i-S_j\geq 0\),也就是 \(S_i\geq S_j\)。
会发现这就是一个顺序对。离散化一下,用树状数组维护一下就好了。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ABC252G Pre-Order
好抽象的区间 dp。
这个题的不便之处在于,一个节点可能有多个儿子,而遍历时会先走编号小的儿子。从而会导致按照根对子树分段的方式会很不固定。
针对这个问题,考虑增加一些辅助维度。令 \(f(l,r)\) 表示 \(p_l\sim p_r\) 组成一棵子树且以 \(p_l\) 为根的方案数,\(g(l,r)\) 表示 \(p_l\sim p_r\) 组成多棵子树且以 \(p_l\) 为根的方案数。
考虑转移。显然 \(f(l,r)\) 可以通过以 \(p_l\) 为根的方式将 \([l+1,r]\) 全部合并成一棵子树,从而
\[f(l,r)=f(l+1,r)+g(l+1,r) \]对于 \(g(l,r)\),可以枚举一个中间点 \(k\in [l+1,r]\) 作为一个树根。为了不重复计算,可以钦定 \([l,k-1]\) 作为一棵单独的子树,\([k,r]\) 任意。从而
\[g(l,r)=f(l,k-1)\times\Big(f(k,r)+g(k,r)\Big) \]时间复杂度 \(\mathcal{O}(n^3)\)。
好像还有什么虚拟根做法,但我完全理解不了啊。
AGC044A Pay to Win
考虑把过程反过来。
- 当 \(2\mid N\) 时,可以花 \(A\) 的代价将 \(N\) 除以 \(2\)。
- 当 \(3\mid N\) 时,可以花 \(B\) 的代价将 \(N\) 除以 \(3\)。
- 当 \(5\mid N\) 时,可以花 \(C\) 的代价将 \(N\) 除以 \(5\)。
- 任意时刻,可以花 \(D\) 的代价将 \(N\) 加上 \(1\) 或减去 \(1\)。
考虑除法的减小速度很快,可以记忆化搜索。
最终搜索被调用的次数大概为 \(1.5\times 10^6\),可以通过。
ABC220F Distance Sums 2
换根 dp。
设 \(f(u)\) 为以 \(u\) 为根的答案。先以 \(1\) 为根 dfs 一遍,得到 \(f(1)\)。
进行第二遍 dfs。设当前已经计算了 \(f(u)\) 的答案,当根换到 \(u\) 的儿子 \(v\) 时,\(v\) 子树中的点深度 \(-1\),\(v\) 子树外的点深度 \(+1\),从而有
\[f(v)=f(u)+n-2\times sz_v \]时间复杂度 \(\mathcal{O}(n)\)。
ABC117D XXOR
考虑高位贪心。对于每一位判断 \(1\) 多还是 \(0\) 多,尽量往反方向选。类似 01-Trie 的贪心过程。
但是这里有一个上界限制。可以用数位 dp 的卡上界思想,如果没有卡住上界就可以随便选,否则不能选超过 \(k\) 这一位。
时间复杂度 \(\mathcal{O}(n\log k)\)。
ABC209E Shiritori
考虑每个单词向下一个能连接的单词连边,如果某个单词没有后继了就是先手必败态。如果一个节点的所有后继都是必败态,它就是必胜态。如果存在一个后继是必胜态,它就是必败态。
而直接暴力枚举建图是 \(\mathcal{O}(n^2)\) 的。考虑一种常见套路,将单词头尾三个字符拿出来哈希,将哈希值看成节点,把单词放在边上,尾向头连边。
做拓扑排序,如果有环就是平局。以每个单词的尾节点状态表示该单词的状态,在每个节点上打标记表示先手胜还是后手胜即可。
时间复杂度 \(\mathcal{O}(n)\)。
ABC283F Permutation Distance
考虑讨论大小关系,拆掉绝对值。
- 当 \(i<j\),\(p_i<p_j\) 时
- \(i<j\),\(p_i>p_j\) 时
- 当 \(i>j\),\(p_i<p_j\) 时
- 当 \(i>j\),\(p_i>p_j\) 时
与 \(i\) 有关的都是定值了。与 \(j\) 有关的用线段树分四次维护,更新答案即可。
以第一种情况为例,从后往前扫,在位置 \(p_j\) 上插入 \(p_j+j\),那么 \(i\) 的答案就是一个后缀最小值。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ABC322F Vacation Query
好久没有这种酣畅淋漓地码线段树的体验了。根本码不对。
很套路。每个线段树节点维护区间长度,前缀最大 \(0/1\) 长度,后缀最大 \(0/1\) 长度和最大 \(0/1\) 长度。反转操作可以用懒标记维护。
注意下传标记时,应该先更新区间信息,再更新区间标记。
时间复杂度 \(\mathcal{O}((n+q)\log n)\)。
ABC105D Candy Distribution
先做一遍前缀和,那么区间 \([l,r]\) 之和为 \(m\) 的倍数等价于 \(S_r\equiv S_{l-1}\pmod m\)。
开一个 map 记录每一种余数 \(r\) 的出现次数,从左往右扫,钦定 \(i\) 为右端点统计答案即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ExaWizards 2019 D Modulo Operations
如果选出的数大于黑板上的数,这次选择不会改变任何事情。也就是说,能对答案起到影响的只有一段前缀最小值。
统计所有方案之和并不好做。考虑转化为统计每个数留在黑板上的方案数。
将 \(a_i\) 倒序排序,设计 dp。令 \(f(i,j)\) 表示考虑前 \(i\) 大的数字,黑板上留下的数为 \(j\) 的方案数。
考虑第 \(i\) 个数怎么放。
- 现在就写上去,则有 $$f(i,j\bmod a_i)\leftarrow f(i,j\bmod a_i)+f(i-1,j)$$
- 放在后面某一个时刻再写上去。由于已经倒序排序,放在后面写就不会再对黑板上的数产生影响了。而这个时刻不放,后面还有 \(n-i\) 个时刻再放,从而 $$f(i,j)\leftarrow f(i,j)+f(i-1,j)\times (n-i)$$
时间复杂度 \(\mathcal{O}(nx)\)。
ABC256F Cumulative Cumulative Cumulative Sum
先把式子拆一拆,看看有什么好处理的东西。
\(B\) 为前缀和数组,即
\[B_x=\sum\limits_{i=1}^x A_i \]\(C\) 为 \(B\) 的前缀和数组,化简即
\[\begin{aligned} C_x&=\sum\limits_{i=1}^x B_i\\ &=\sum\limits_{i=1}^x\sum\limits_{j=1}^i A_j\\ &=\sum\limits_{i=1}^x (x-i+1)A_i \end{aligned} \]\(D\) 为 \(C\) 的前缀和数组,化简即
\[\begin{aligned} D_x&=\sum\limits_{i=1}^x C_i\\ &=\sum\limits_{i=1}^x\sum\limits_{j=1}^i (i-j+1)A_j\\ &=A_1\sum\limits_{i=1}^xi+A_2\sum\limits_{i=1}^{x-1}i+\cdots+A_x\\ &=\dfrac{x(x+1)}{2}A_1+\dfrac{(x-1)x}{2}A_2+\cdots+\dfrac{1\times 2}{2}A_x\\ &=\sum\limits_{i=1}^x\dfrac{(x-i+1)(x-i+2)}{2}A_i\\ &=\sum\limits_{i=1}^x\dfrac{i^2-(2x+3)i+(x+1)(x+2)}{2}A_i\\ &=\dfrac{1}{2}\sum\limits_{i=1}^xi^2A_i-\dfrac{2x+3}{2}\sum\limits_{i=1}^xiA_i+\dfrac{(x+1)(x+2)}{2}\sum\limits_{i=1}^xA_i \end{aligned} \]用三个树状数组分别维护 \(i^2A_i,iA_i,A_i\) 的前缀和即可。单点查询可以直接修改。
时间复杂度 \(\mathcal{O}(q\log n)\)。
ARC077E guruguru
暴力枚举最适亮度的值显然复杂度过高。
设 \(c_i\) 表示最适亮度设为 \(i\) 时的答案。对于 \(a_i\rightarrow a_{i+1}\) 的修改,考虑其对每一个 \(c_x\) 的影响。
分类讨论:
-
当 \(a_i<a_{i+1}\) 时:
-
对于 \(1\leq x\leq a_i+1\),此时不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}-a_i)\)。
-
对于 \(a_i+2\leq x\leq a_{i+1}\),此时跳到 \(x\) 再不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}-x+1)\)。
-
对于 \(a_{i+1}+1\leq x\leq m\),此时不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}-a_i)\)。
-
-
当 \(a_i>a_{i+1}\) 时:
-
对于 \(1\leq x\leq a_{i+1}\),此时先跳到 \(x\) 再不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}-x+1)\)。
-
对于 \(a_{i+1}+1\leq x\leq a_i+1\),此时不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}+m-a_i)\)。
-
对于 \(a_i+2\leq x\leq m\),此时先跳到 \(x\) 再不断 \(+1\) 最优,故有 \(c_x\leftarrow c_x+(a_{i+1}+m-x+1)\)。
-
注意到这只需要维护区间加以及区间加等差数列,对 \(c\) 序列进行二阶差分即可。
具体地,设 \(c\) 的差分数组为 \(d\),考虑上面的每一种操作对 \(d\) 带来的影响:
-
当 \(a_i<a_{i+1}\) 时:
-
对于 \(x=1\),此时 \(d_x\leftarrow d_x+(a_{i+1}-a_i)\)。
-
对于 \(2\leq x\leq a_i+1\),此时 \(d_x\) 不会改变。
-
对于 \(a_i+2\leq x\leq a_{i+1}\),此时 \(d_x\leftarrow d_x-1\)。
-
对于 \(x=a_{i+1}+1\),此时 \(d_x\leftarrow d_x+(a_{i+1}-a_i-1)\)。
-
对于 \(a_{i+1}+2\leq x\leq m\),此时 \(d_x\) 不会改变。
-
-
当 \(a_i>a_{i+1}\) 时:
-
对于 \(x=1\),此时 \(d_x\leftarrow d_x+a_{i+1}\)。
-
对于 \(2\leq x\leq a_{i+1}\),此时 \(d_x\leftarrow d_x-1\)。
-
对于 \(x=a_{i+1}+1\),此时 \(d_x\leftarrow d_x+(a_{i+1}+m-a_i-1)\)。
-
对于 \(a_{i+1}+2\leq x\leq a_i+1\),此时 \(d_x\) 没有变化。
-
对于 \(a_i+2\leq x\leq m\),此时 \(d_x\leftarrow d_x-1\)。
-
再对 \(d\) 做一次差分后用二次前缀和即可得到 \(c\) 数组。答案即为 \(c\) 中的最小值。
时间复杂度 \(\mathcal{O}(n)\)。
ABC167D Teleporter
注意到 \(K\leq 10^{18}\),说明一定存在循环节。每个点出度恰为 \(1\),找循环节就是在基环树上找环。
从 \(1\) 号点开始遍历,第一次访问时打上时间戳,直到重复遍历到某个点,时间戳相减便可以求出环的长度和进入环的时间戳。最后只需要判断 \(K\) 是否已经进入了环即可。
时间复杂度 \(\mathcal{O}(n)\)。
ABC223F Parenthesis Checking
判断合法括号序列的经典做法是将左括号看成 \(1\),右括号看成 \(-1\),做一遍前缀和。任意位置的前缀和非负且总和为 \(0\) 即为合法括号序列。
考虑建一棵线段树,维护每个位置上的前缀和。
对于修改操作:
- 若 \(s_l=s_r\) 则可以不操作。
- 若 \(s_l\) 为左括号且 \(s_r\) 为右括号,相当于在线段树上对 \([l,r-1]\) 区间 \(-2\)。
- 若 \(s_l\) 为右括号且 \(s_r\) 为左括号,相当于在线段树上对 \([l,r-1]\) 区间 \(+2\)。
对于询问操作,可以单点查询 \(l-1\) 和 \(r\) 上的前缀和,如果相等说明子串总和为 \(0\)。同时维护区间最小值,若最小值等于 \(l-1\) 位置上的前缀和说明区间任意位置前缀和非负。
时间复杂度 \(\mathcal{O}((n+q)\log n)\)。
ABC242G Range Pairing Query
就当作复习莫队了。
莫队板子。开一个桶维护区间每种颜色的数目即可。
注意莫队的写法,区间先扩展再收缩才是正确的。
ABC187F Close Group
子集 dp。设 \(f(S)\) 表示将点集为 \(S\) 的子图的答案。
当 \(S\) 本身为完全图时有 \(f(S)=1\),否则枚举 \(S\) 的子集 \(T\),\(S\) 的答案即为 \(T\) 和 \(\complement_ST\) 的答案之和。
转移方程为
\[f(S)=\min_{T\subseteq S}\left\{f(T)+f\left(\complement_ST\right)\right\} \]时间复杂度 \(\mathcal{O}(3^n)\)。
关于判断完全图,可以记 \(E_u\) 为与 \(u\) 直接相连的点集。点集为 \(S\) 的子图构成完全图当且仅当对于所有 \(u\in S\) 都有 \(S\subseteq E_u\)。这一部分的预处理容易做到 \(\mathcal{O}(n2^n)\)。
ARC139B Make N
如果 \(AX\leq Y\),那么操作 \(2\) 就可以被操作 \(1\) 替代。同理若 \(BX\leq Z\),那么操作 \(3\) 就可以被操作 \(1\) 替代。若有一种操作被替代,只需要贪心地使用单价更低的,最后再用 \(1\) 补齐即可。
现在只需要考虑 \(AX>Y\) 且 \(BX>Z\) 的情况。不妨设 \(\dfrac{Y}{A}\leq \dfrac{Z}{B}\),即让操作 \(2\) 的单价更低。
注意到操作 \(2\) 只需要使用不超过 \(\left\lfloor\dfrac{N}{A}\right\rfloor\) 次,否则 \(P\) 会超过 \(N\)。而操作 \(3\) 只需要使用不超过 \(A-1\) 次,否则可以将 \(A\) 次操作 \(3\) 替换为 \(B\) 次操作 \(2\) 而使得答案减少。
考虑根号分治:
- 若 \(A\geq\sqrt{N}\),枚举操作 \(2\) 的使用次数,贪心地用操作 \(3\),剩下的用操作 \(1\) 补齐。
- 若 \(A<\sqrt{N}\),枚举操作 \(3\) 的使用次数,贪心地用操作 \(2\),剩下的用操作 \(1\) 补齐。
时间复杂度 \(\mathcal{O}(T\sqrt{N})\)。
ABC199E Permutation
先把所有限制按照 \(X_i\) 排序,从小到大依次考虑每条限制。
看到 \(n\leq 18\),不妨考虑状压。设 \(f(S)\) 表示选取集合为 \(S\) 且满足所有 \(X\leq |S|\) 的限制的方案数。这个状态设计允许我们加入一个新数时只考虑 \(X=|S|+1\) 的限制。转移是平凡的。
现在需要快速判断集合 \(S\) 是否满足若干条形如「小于等于 \(Y_i\) 的数不超过 \(Z_i\) 个」的限制。我们把表示 \(S\) 的二进制数中最后 \(Y_i\) 位拿出来,如果这些位置上的 \(1\) 不超过 \(Z_i\) 个即为合法。可以做到时间复杂度 \(\mathcal{O}(1)\)。
时间复杂度 \(\mathcal{O}(n2^n)\)。
ABC234E Arithmetic Number
发现公差不为 \(0\) 的最大等差数是 \(9876543210\),说明当 \(X\geq 10^{10}\) 之后的等差数只能为一个数字重复若干遍,这就很好判断了。
考虑 \(X<10^{10}\) 的情况。打个表发现等差数很少,考虑把所有等差数存起来,直接二分即可。
时间复杂度近似 \(\mathcal{O}(1)\)。
ARC060E Tak and Hotels
先二分出来每个点向后能跳到的最远点。但是暴力跳还是不能接受。
考虑分块,维护从点 \(i\) 跳出其所在块的最小步数。这样一次就可以跳 \(\sqrt{n}\) 个点。
时间复杂度 \(\mathcal{O}(n\log n+q\sqrt{n})\)。
ABC231F Jealous Two
形式化一点,就是求数对 \((i,j)\) 的个数,使得 \(a_i\geq a_j\) 且 \(b_i\leq b_j\)。
按照 \(a_i\) 升序为第一关键字,\(b_i\) 降序为第二关键字排序。顺序扫一遍,用树状数组记录 \(b_i\) 即可。
需要注意,如果 \((a_i,b_i)=(a_j,b_j)\) 应该被计算两次。所以需要对于这种情况拿出来单独计算。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ARC137A Coprime Pair
神秘题。
当枚举到两个素数时直接就对了。然后就有一个非常抽象的结论:在题设下不超过 \(1500\) 个数中就会出现一个素数。从大到小枚举区间长度,暴力做就行了。
时间复杂度 \(\mathcal{O}(k^2\log R)\),其中 \(k\leq 1500\)。
ABC235E MST + 1
考虑新加入的一条边,如果最小生成树上的最大边权小于这条边,那么就可以让这条边加进去。所以只需要维护路径最大边权即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ABC194E Mex Min
固定区间长度的问题,不难想到滑动窗口。
加入队尾和删除队首都很好计算答案,上一个类似单调队列的方法就做完了。
时间复杂度 \(\mathcal{O}(n)\)。
ABC280F Pay or Receive
首先,走不到当且仅当起点和终点不在一个连通块内。用并查集维护一下。
如果 \(X\) 到 \(Y\) 的路径上存在正环,答案就是 \(+\infty\)。由于这个图的性质,如果路径上存在正环,那么把环上路径全都反向就会得到负环。所以存在正环或负环答案都是 \(+\infty\)。
现在图上没有正环和负环,如果还有环只能是零环。由于这个图的性质,零环上 \(u\rightarrow v\) 两个方向的路径是相等的,只需要走任意一条路径就可以确定两点之间距离。
本来判负环的复杂度是 \(\mathcal{O}(nm)\)。现在从任意一点搜索,如果一个点 \(u\) 能被松弛第二遍,说明图中不只有零环,还有正环或负环,那么所有与 \(u\) 处于一个连通块的点的答案都是 \(+\infty\)。
现在得到了某个源点 \(s\) 到其他所有点的距离,则 \(u\rightarrow v\) 的的路径可以拆成 \(u\rightarrow s\rightarrow v\)。因为边要反向,从而答案为 \(dis_v-dis_u\)。
时间复杂度 \(\mathcal{O}(n+m)\)。
JOI2017 Foehn Phenomena
题目给了很强的提示性,容易想到差分。
会发现修改操作 \([l,r]\) 对于区间内部和外部的答案都是没有影响的,有影响的只有边界。先统计一下初始的答案,修改之后调整一下答案即可。
时间复杂度 \(\mathcal{O}(n + q)\)。
JOI2017 Kingdom of JOIOI
理解题意后发现只需要将正方形网格切成两个凸多边形。设两块区域分别为 \(A,B\),考虑全局最大值 \(M\) 和全局最小值 \(m\),我们肯定希望把他们尽可能放在不同的区域内。不妨钦定 \(M\in A\),\(m\in B\)。
考虑二分答案 \(k\),则 \(A\) 内的数 \(x\) 需要满足 \(M-k\leq x\leq M\),\(B\) 内的数 \(y\) 需要满足 \(m\leq y\leq m+k\)。从而所有 \(x>m+x\) 都要被归入 \(A\) 中,所有 \(x<M-k\) 都要被归入 \(B\) 中。
现在这些点已经确定了需要归入的集合。如果存在一条“阶梯状”的分界线能够将这些点划分到两个集合内,则说明 \(x\) 成立,可以在更小区间二分。
现在只需要找分界线。不妨钦定分界线从左上向右下延伸,且左边为 \(B\),右边为 \(A\)。
先从上到下扫描。对于每一行 \(i\),找满足 \(a_{i,j}>m+k\) 的最小的 \(j\),这就是 \(B\) 集合的边界位置。同理从下到上扫描,对于每一行 \(i\),找满足 \(a_{i,j}<M-k\) 的最大的 \(j\),这就是 \(A\) 集合的边界位置。显然,合法的切割方案不会出现边界重合或相交的情况。
我们只处理了一个方向的切割。只需要做一次转一次网格即可。又由于旋转会导致行列颠倒,不方便计算,可以通过上下翻转和左右翻转达到同样的效果。
时间复杂度 \(\mathcal{O}(nm\log a)\)。
ABC184F Programming Contest
注意到 \(n\leq 40\) 非常具有提示性。
考虑折半搜索,计算序列前一半和后一半分别能凑出哪些数,装进 vector 排序二分。
计算一半的序列就很好办了,可以搜索可以状压。
时间复杂度 \(\mathcal{O}(n\times 2^{\frac{n}{2}})\)。
ABC320E Somen Nagashi
用两个 set 分别维护当前在队内的人和出队的人。每一个事件 \(t\) 发生之前,先把出队的人中归队时刻 \(\leq t\) 的入队,把伤害累加到队首上,再将队首出队即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。
注意:set 一定要定义清楚严格的优先级,不能模棱两可,否则会出现排序错误。
AGC020C Median Sum
注意到如果能凑出 \(x\),那么也可以凑出 \(\sum a_i-x\)。说明子集和是对称的,我们只需要找到最靠近总和的一半的拼法。
这就变成了 01 背包。找到所有能凑出的数,用总和的一半向上扫即可。
用 bitset 优化即可做到 \(\mathcal{O}\left(\dfrac{\sum a_i}{w}\right)\)。
标签:记录,复杂度,leq,提交,mathcal,杂题,sum From: https://www.cnblogs.com/duckqwq/p/18132127