一维数组的地址计算
设每个元素的大小是 \(size\),首元素的地址是 \(a[1]\) ,则
a[i] = a[1] + (i-1)*size
若首元素的地址是 \(a[0]\)
则a[i] = a[0] + i*size
二维数组的地址计算 (\(m * n\)的矩阵)
行优先
设每个元素的大小是 \(size\) ,首元素的地址是 \(a[1][1]\) ,则 \(a[i][j]\) ?
分析:\(a[i][j]\) 位于第 \(i\) 行,第 \(j\) 列。它之前有 \(i-1\) 行,在第 \(i\) 行它之前有 \(j-1\) 个元素。
即 \(a[i][j] = a[1][1] + [n*(i-1) + (j-1)]*size\)
三维数组的地址计算 (\(r*m*n\)) \(r\) 行 \(m\) 列 \(n\) 纵
行优先
首元素的地址 \(a[1,1,1]\)
\(a[i,j,k] = a[1,1,1] + [(i-1)*n*m + (j-1)*n + (k-1)]*size\)
压缩存储:指为多个值相同的元素只分配一个存储空间,对零元素不分配存储空间,其目的是为了节省存储空间。
二维数组通常用来存储矩阵,特殊矩阵分为两类:
(1)元素分布没有规律的矩阵,按照规律对用的公式实现压缩。
(2)无规律,但非零元素很少的稀疏矩阵,只存储非零元素实现压缩。
一、三角矩阵
包括上三角矩阵,下三角矩阵和对称矩阵
(1)若 \(i<j\) 时,\(a[i,j]=0\) ,则称此矩阵为下三角矩阵。
(2)若 \(i>j\) 时,\(a[i,j]=0\),则称此矩阵为上三角矩阵。
(3)若矩阵中的所有元素满足 \(a[i,j]=a[j,i]\) ,则称此矩阵为对称矩阵。

二、三对角矩阵
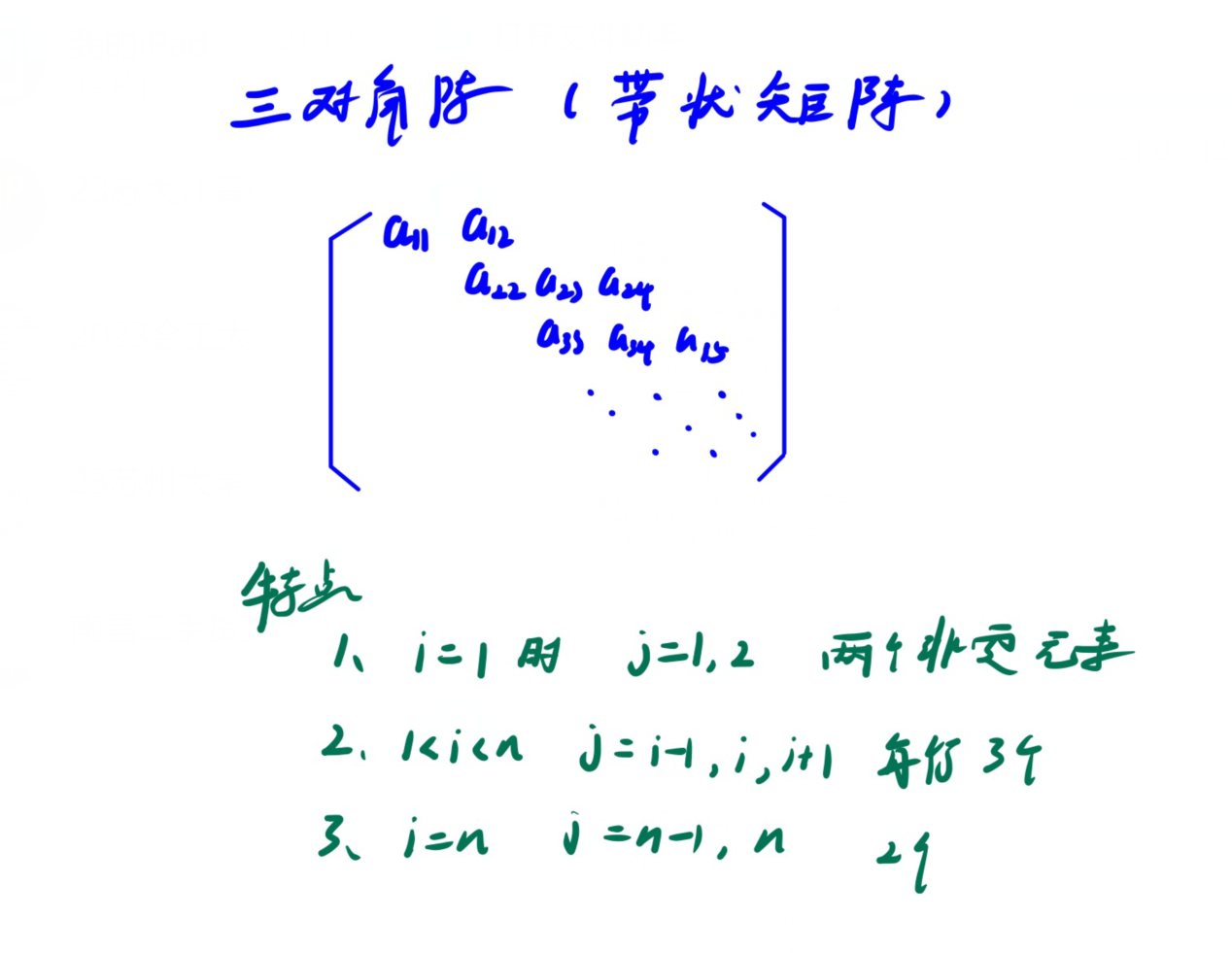
带状矩阵的压缩方法:将非零元素按照行优先存入一维数组。
(1)确定一维数组的存储空间大小:\(2+(n-2)*3+2 = 3n-2\)
(2)确定非零元素在一维数组中的地址
$loc(i,j) = loc(1,1) + $ 前 \(i-1\) 行非零元素个数 \(+\) 第 \(i\) 行中 \(a[i,j]\) 前非零元素的个数
前 \(i-1\) 行:\(3 * (i-1) - 1\),因为第一行只有两个,所以要减去 \(1\)
第 \(i\) 行中 \(a[i,j]\) 前非零元素的个数 \(=(j-i)+1,\)
\(j-i\) 有三种情况:
(1)\(j<i ,j-i=-1\)
(2)\(j==i\) **\(,j-i=0\) **
(3)\(j>i ,j-i=1\)
\[loc(i,j) \\= loc(1,1) + 3(i-1)-1 + j-i+1 \\= loc(1,1) + 2(i-1) + j-1 \\= loc(1,1) + 2i+j-3 \] 标签:loc,元素,矩阵,地址,数组,DS,size From: https://www.cnblogs.com/RioTian/p/16795070.html