4.6 模拟赛
T1 困难的图论
题意:找出所有 在且仅在 1 个简单环中的边,输出编号的异或和。
一个错误的想法:找边双连通分量,看边数是否等于点数
反例: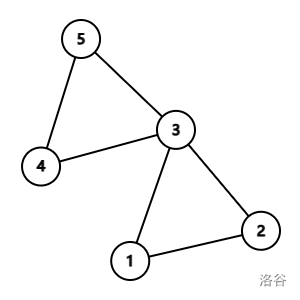
正解是点双
所以我在想,为什么是点双,不是边双呢?
什么时候找点双,什么时候找边双呢?
T2 中等的字符串
已知 \(m\) 个关键词 \(s_i\),每出现一次得分 \(a_i\),求一个未知的长度为 \(n\) 的文本,最大得分是多少。
数据范围:\(n\le 10^{12},m\le 100,\sum |s_i|\le 200,a_i\le 200\)
显然 AC 自动机上 dp,但是 1e12
key:矩阵优化 AC 自动机上 dp
非常神奇。
我们发现转移方程是 \(f_{i,j}=\max\{f_{i-1,k}+val(j,k)\}\)
其中 val 代表从 \(j\) 点走到 \(k\) 点的贡献,如果走不到就是负无穷。
在上面这个式子里,\(j\) 到 \(k\) 只能走一步,考虑能不能结合起来多走几步(因为 \(n\) 是步数)。
发现 \(f_{i,j}\) 其实就是走 \(i\) 步意义下的 \(val(0,j)\),故满足结合律,可以类似矩阵乘求 \(val(j,k)\)。
复杂度 \(O((\sum|s_i|)^3\log n)\)
T3 上网
知道一些信息:
- 值域 \([1,10^9]\)
- \(x_{p_i}=d_i\)
- 对于下标区间 \([L_i,R_i]\),可以分成“大组” \(S\) & “小组” \(T\),满足 \(\forall i\in S,j\in T,x_i>x_j\)
求一个可行的构造方案。
整体思路:大小关系建成 DAG,拓扑排序赋值。
30pts:暴力 \(O(n^2)\) 建边
50pts:每个信息设定中间点,用边权区分,\(O(nm)\) 建边
正解:线段树优化建边,\(O(k\log n)\)
先像线段树一样,每个点表示区间最大值,和子节点之间连边权为 0。
每个信息:
- 找出 \(k\) 个点分隔开的 \(k+1\) 个区间
- 每个区间找到线段树对应的 \(\log n\) 个区间
- 新建一个点 \(x\) 表示这些区间的最大值
- x 与这些区间连边权为 0
- k 个点与 x 连边权为 1