题意:给出一个 \(n\) 个点的树(边权为 \(1\))和集合 \(S\),求有多少个点集 \(T\) 可以被表示为离 \(S\) 中的一个点 \(u\) 距离不超过 \(d\) 的点构成的集合(下文称为 \(u\) 的 \(d\) 级邻域)。
考虑 \(S\) 为所有点的特殊情况:
我们直接求每个点邻域的个数再求和,会算重一些点集,这种情况发生仅当这个邻域在某些方向“满了”,从而可以认为是向没满的方向移动一些并把这个点当作邻域的中心。
如下图中的黑色点集既可以表示为 \(v\) 的 \(3\) 级邻域也可以表示为 \(u\) 的 \(2\) 级邻域。

于是我们考虑在点集的“中心”,即邻域的 \(d\) 最小时统计,容易发现对于所有不是全集的某个邻域,都存在唯一的一个点 \(u\) 使得邻域的 \(d\) 最小(尽可能不溢出),于是我们单独统计全集,接下来考虑枚举一个点并统计它作为中心的邻域。
令 \(f_u\) 表示 \(u\) 在树上最远点的距离,\(g_u\) 表示次远点的距离,容易换根求出 \(f_u,g_u\)。
首先 \(d\) 不能取 \(\geq f_u\) 的值,因为我们现在只统计不是全集的集合。
接下来考虑 \(u\) 是中心的条件:不能存在某个相邻的 \(v\) 使得 \(v\) 的 \(d-1\) 级领域和 \(u\) 的 \(d\) 级领域相同,可以发现这种情况仅当除了 \(v\) 方向的其它方向的子树内都是满的,显然 \(v\) 只能在 \(f_u\) 所在子树的方向,且其它方向最远距离的点的距离都 \(\leq d-2\)。(在 \(v\) 处 \(d-1\) 也能统计到)于是我们得到 \(d\) 不能取 \(\geq g_u+2\) 的值。
则 \(u\) 可以选择的 \(d\) 在 \([0,\min(f_u-1,g_u+1)]\) 任意取,对所有值求和后加上全集即可。
接下来并不是所有点都可以选了,但我们仍然考虑在邻域邻域的中心 \(u\) 处统计答案,即使这个中心并不能选择(我们统计的其它某个可以选的 \(v\) 的 \(d_1\) 级邻域但因为溢出而以 \(u\) 为中心)。
若 \(u\) 可以选择,则它作为中心的情况和上面相同。
若 \(u\) 不能选择,则需要 \(u\) 某个方向的一个可选择的 \(v\),填满它的子树并从 \(u\) 向外延伸向其它方向。
我们把 \(u\) 当作中心的话,需要这个 \(v\) 所在的子树被填满(这样才能使中心向 \(u\) 偏移,否则中心显然不能是 \(u\)),并向外蔓延的距离至少要比这个子树的深度大,才可以把 \(u\) 当作中心。
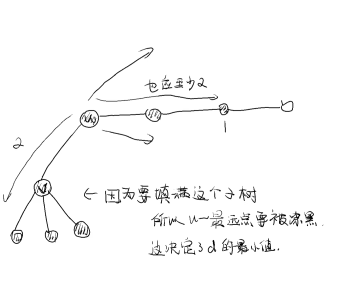
所以考虑 \(d\) 能够取的最小值,即所有存在可以选择的点 的子树中,最深点深度的最小值,称为 \(h_u\),通过换根求出即可,那么这个点可取的区间即 \([h_u,\min(f_u-1,g_u+1)]\),对所有点求和再加上全集即可。
其实最开始解决这个问题时,我采用的办法是树定一个根,然后对于每个点集在可行的最靠上的 \(u\) 的邻域统计。
在解决 \(S\) 为所有点的情况时还可以用类似的办法解决(在钦定邻域中心不能上移的位置统计),但是无法拓展到 \(S\) 不是全集的情况。
这启示我们在统计无根树问题的时候,最好还是采用更加「无根」的统计方式,比如“中心”、“重心”、“最近”之类的,而不是“公共祖先”、“最上方”之类的有根树方向。
标签:AGC008F,中心,题解,邻域,点集,方向,全集,换根,统计 From: https://www.cnblogs.com/Dreamerkk/p/18112488