1 基环树概念

1.1 定义

首先，基环树并不是一颗严格的树。它是一张由 \(n\) 个节点，\(n\) 条边组成的图。

1.2 无向联通图上的基环树

首先，一棵树有 \(n\) 个节点，\(n-1\) 条边。那么基环树就可以看做是在一棵树上加了一条边，这样多出了一个环（因此基环树也被称作环套树）。

如下图所示：

1.3 有向联通图上的基环树

有向图上根据边的方向再次分为两类

1.3.1 内向树

每个节点的出度为 \(1\)，如下图：

1.3.2 外向树

每个节点的入度为 \(1\)，如下图：

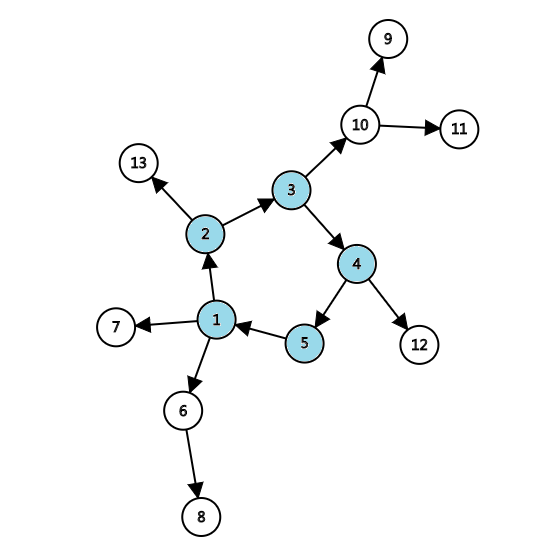
1.4 非联通图上的基环树

如果整个图非联通，那么又会形成基环树森林、基环外向树森林、基环内向树森林。

2 基环树处理方式

上面的定义其实对于做题没有什么帮助，同时基环树的题目通常也要结合树形或环形 dp 求解。下面介绍一些基本处理方式。

2.1 找环

最基本的一步：先找出基环树中环在哪里。

以无向连通图为例，代码很好想也很好实现：

void dfs(int u, int fa) {
	if(ins[u]) {//在栈内，说明又走回来了
		int v;
		mark[u] = 1;
		while(s[top] != u) {//这些节点均为环上的点
			mark[s[top]] = 1;
			top--;
		}
		return ;
	}
	if(vis[u] == 1) return ;//已经访问（访问并不等价于在栈中）
	s[++top] = u;
	vis[u] = ins[u] = 1;
	for(int i = head[u]; i; i = edge[i].nxt) {
		int to = edge[i].to;
		if(to == fa) continue;
		dfs(to, x);
	}
	top--;
	ins[u] = false;//弹出栈
	return;
}

2.2 树形 dp 处理

由于基环树与普通的树十分接近，因此可以考虑去掉环上的一条边，使整张图变为一颗树之后再开始 dp。

又因为我们删去了一条边，所以会有两个点的关系被删除，所以这种方法一般要 dp 两次。

2.3 环形 dp 处理

首先我们将环拎出来，这样就可以看成是一些树挂在这个环上。我们将所有子树的信息算出来之后合并到环上的节点，这样就可以环形 dp 求解了。

3 例题

对于基环树，概念是没有什么用的，所以直接看一道例题。

3.1 [ZJOI2018] 骑士

首先这道题和 没有上司的舞会 很像，只是变成了基环树。

我们考虑树形 dp 处理，先求出环上的一条边，以这条边上的两点作树形 dp，分别得到 \(f(x,0)\) 和 \(g(y,0)\)。

由于两者只能取一，所以在两个答案中取 \(\max\) 即可。

剩下的注意细节。

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef long long LL;
const int Maxn = 2e6 + 5;

int n, w[Maxn];

int head[Maxn], edgenum = 1;
struct node {
	int nxt, to;
}edge[Maxn];

void add(int from, int to) {
	edge[++edgenum] = {head[from], to};
	head[from] = edgenum;
}

int st, ed, num;
int vis[Maxn], ins[Maxn];

void fcir(int x, int fa) {
	if(vis[x]) return ;
	vis[x] = ins[x] = 1;
	for(int i = head[x]; i; i = edge[i].nxt) {
		int to = edge[i].to;
		if(to == fa) continue;
		if(ins[to]) {
			st = x, ed = to, num = i;
			continue;
		}
		fcir(to, x);
	}
	ins[x] = 0;
}

int dp[Maxn][2];

void dfs(int x, int fa) {
	dp[x][0] = 0;
	dp[x][1] = w[x];
	for(int i = head[x]; i; i = edge[i].nxt) {
		int to = edge[i].to;
		if(to == fa) continue;
		if(i == num || (i ^ 1) == num)  {
			continue;
		}
		dfs(to, x);
		dp[x][0] += max(dp[to][0], dp[to][1]);
		dp[x][1] += dp[to][0];
	}
}

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n;
	for(int i = 1; i <= n; i++) {
		int v;
		cin >> w[i] >> v;
		add(i, v), add(v, i);
	}
	int ans = 0;
	for(int i = 1; i <= n; i++) {
		if(vis[i]) continue;
		fcir(i, 0);
		dfs(st, 0);
		int ans1 = dp[st][0];
		memset(dp, 0, sizeof dp);
		dfs(ed, 0);
		ans += max(ans1, dp[ed][0]);
	}
	cout << ans ;
	return 0;
}