前言
一日知基环树弱,固补题。
关于基环树
基环树定义
一个环,环上每个点都有一颗以该点为根的树,如下图为一棵基环树
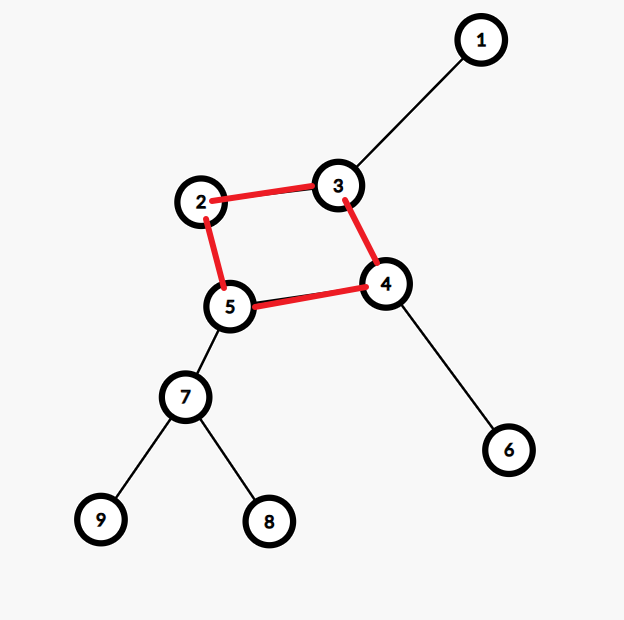
关于基环树常规思路
通常来说基环树常规思路是先处理环上树的结果,后通过树的结果来处理换上结果。
具体处理方式依照题目来定。
然而只是通常来说
因为基环树的问题灵活性强且就算没专门学过基环树的也能做出基环的题,所以 OIwiki 也没有该算法的具体讲解。
典题
题目描述
给定一个 \(n\) 个点 \(m(1\le m\le n)\) 条边的无向图,并保证该图联通。
选定一个出发,当走到 \(s\) 时,可执行两种操作:
- 规则1 走向与 \(s\) 相连且未经过的点
- 规则2 定义 \(u\) 走向的 \(s\),走向 \(u\) 。(口语化表述即为退回)
每当第一次经历一个点 \(s\) ,将 \(s\) 放入序列 \(ans\) ,需要保证经过每一个点。
求对于该图字典序最小的 \(ans\) 。
输入格式
输入共 \(m + 1\) 行。第一行包含两个整数 \(n,m(m ≤ n)\),中间用一个空格分隔。
接下来 m 行,每行包含两个整数 \(u,v (1 ≤ u,v ≤ n)\) ,表示编号为 \(u\) 和 \(v\) 的点之间有一条边,两个整数之间用一个空格分隔。
输出格式
输出包含一行,\(n\) 个整数,表示字典序最小的序列。相邻两个整数之间用一个空格分隔。
数据规模与约定
对于 \(100\%\) 的数据和所有样例, $1 \le n \le 5000 $ 且 \(m = n ? 1\) 或 \(m = n\) 。
Solution
思路
对于 \(n-1\) 条边的联通无向图,显然是一棵树。此时只需要从 \(1\) 出发,每次贪心深搜即可。
对于 \(n\) 条边的连通无向图,我们发现恰好符合基环树的性质。但无论 \(1\) 是否在环上,我们都需要从 \(1\) 点出发保证答案字典序最小。
首先考虑 \(1\) 在环上的情况。通过题目给出的两个规则,我们可以发现,从 \(1\) 出发,若走到环上一个点后按照环的原路返回到点 \(1\) ,则点 \(1\) 无法再次向走向刚才走过的那些点。
所以环上走的方案只有两种可能,如下:
`- 绕着环走一次
 `
`
- 绕着环走的过程中返回 \(1\),并往另一个方向走。
实际上,这两种方案可以抽象成一种情况,第一种情况相当于绕一圈再返回起点,即为第二种的特殊情况。
也就说,我们当前需要解决的就是判断何时返回。根据题目规则2,显然能够发现,在反向走环过程中,我们必须要将 以环上点为根节点 的树全部走完。
考虑贪心,当我们正向走环的时候,当走到点 \(u\) ,我们显然可以求出从 \(u\) 开始反向走边字典序最小的下一个新遇到的点 \(v\) 。
- 若走到 \(u\) 点的过程中环上的所有树均已走过,则 \(v\) 为 \(1\) 反向的第一个点。
- 若走到 \(u\) 点的过程中环上有树未走完,则 \(v\) 为距离 \(u\) 最近的一颗未走完的树上最小的未走过的子节点。
此时,若 \(v\) 小于 \(u\) 正向走到的下一个环上的点,则开始返回。然后就能得到字典序最小的序列了。
然后考虑 \(1\) 不在环上的情况。
为了字典序最小,显然还是要从 \(1\) 开始走,先按照走树的贪心策略走,若走的过程中进入环,则将第一次进入环的点作为起始点,无视,该点与父节点连的边,按照环的处理方式处理该环即可。
具体细节代码中有具体注释。
代码
#include<bits/stdc++.h>
using namespace std;
#define Pair pair<int,int>
#define mk make_pair
const int N=5e3+7;
int n,m;
vector<int> nxt[N];
bool vis[N],flt[N];
bool flag=false;
queue<int> ans;
void cir(int it,int fa,int be){
vis[it]=true;
for(int v:nxt[it]){
if(v==fa) continue;
if(v==be) flag=true;
if(vis[v]) continue;
cir(v,it,be);
}
}
void find_circle(){
for(int i=1;i<=n;++i){
flag=false;
memset(vis,0,sizeof(vis));
cir(i,0,i);
if(flag){
flt[i]=true;
}
}
}
bool ret=false;//记录是否回退
void dfs(int it,int fa,int minn){
cout<<it<<" ";
priority_queue<int,vector<int>,greater<int> > qu;
vis[it]=true;
ans.push(it);
//init
int maxt=0,mint=0x3f3f3f3f;
for(int v:nxt[it]){
if(vis[v]) continue;
qu.push(v);
if(flt[v]){
mint=min(mint,v);
maxt=max(maxt,v);
}
}
//非环
if(!flt[it]){
while(!qu.empty()){
dfs(qu.top(),it,minn);
qu.pop();
}
}
else{//环
int xtt=minn;
if(!xtt&&maxt!=mint) xtt=maxt;//记录环的另一端,注意若1在环中会导致maxt=mint然后莫名其妙回溯导致23wa
while(!qu.empty()){
int nxt=qu.top();
qu.pop();
if(vis[nxt]) continue;//防止再次走环的另一端
if(flt[nxt]){//绕着环走
if(flt[fa]&&xtt<nxt&&!ret&&qu.empty()){//若可回溯支链(或环的另一端)最小小于下一个环的点且曾经没回退过并且当前无支链小于绕环,则可以退回
ret=true;
continue;//跳过并走完支链后方可回溯
}
// cout<<it<<"->"<<nxt<<endl;
dfs(nxt,it,(!qu.empty() ? qu.top():xtt));//选择绕环并去传递可回溯支链的最小
}
else{//走支链
// cout<<it<<"->"<<nxt<<endl;
dfs(nxt,it,minn);
}
}
}
}
void solve(){
memset(vis,0,sizeof(vis));
dfs(1,0,0);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;++i){
int u,v;
cin>>u>>v;
nxt[u].push_back(v);
nxt[v].push_back(u);
}
find_circle();
solve();
return 0;
}