首先考虑题目要求每条边被经过两次,这说明了我们进入一个子树后一定会处理完子树内所有的叶子后离开该子树,否则子树上端那条边会进出至少两次,即经过至少四次。所以这说明了子树之间的独立性:某个子树在答案中一定是一个连续的区间,这引导我们从有根树信息自下向上拼接的角度考虑。
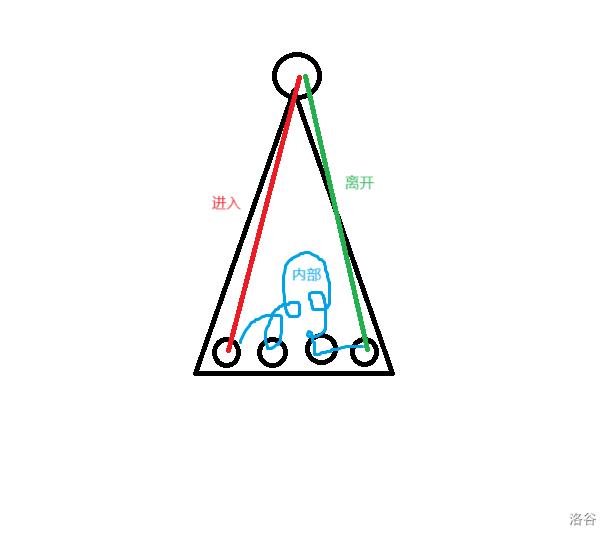
我们就可以将一个有根树抽象成三部分:从根进入 \(in\),内部最大值 \(max\),离开回到根 \(out\)。内部的部分不会再发生改变,我们只关心它的最大值 \(max\),然后可以通过拼接两个子树离开-进入的信息来得到父亲的信息:\((in_a,out_b,\max(max_a,max_b,out_a+in_b))\)。
因为这个过程是可以倒过来走的,于是我们就只需要设置 \(f_{a,b}\) 表示进入左子树的 \(a\),从右子树的 \(b\) 离开的最大值的最小值即可。
于是我们通过记录所有每个点所有 \((in,out)\) 对应的 \(max\) 就有了一个 \(O(\text{poly}(n))\) 的做法(取决于你咋搞,反正难以低于 \(O(n^2)\))。
考虑优化:若要记录内部最大值是一件很浪费的事情,我们需要最小化最大的一次,又因为我们的过程涉及到了边的加和,故肯定得考虑二分答案转化为可行性问题,问题变为需要检测答案 \(Dis\) 是否可行。
然后对于刚刚那个问题,我们便不再关心每个 \((in,out)\) 了,我们只关心每个 \(in\) 值可以对应的 \(out\),且如果存在 \(in_1 \geq in_1,out_1 \geq out_2\),那么 \((in_1,out_1)\) 一定没用,于是我们可以通过维护一组单增的 \(in\) 及其对应的一组单减的 \(out\) 值来描述这个子树的信息。
考虑信息的拼接,即需要合并两组 \(A(in,out),B(in,out)\),合并的条件为若有 \(Aout_i + Bin_j \leq Dis\) 则有 \((Ain_i,Bout_j)\),因为 \(A\) 和 \(B\) 都满足随着 \(in\) 增,\(out\) 减,所以可以按顺序枚举 \(Aout_i\) 双指针维护可行的 \(Bin_j\) 即可。因为过程是可以倒过来走的,我们再把所有 \((out,in)\) 也加入,最终再排序/归并排序,去除掉没用的就可以得到父亲树内的 \((in,out)\) 序列。
直接这样做看上去复杂度是 \(O(\sum siz_i)=O(n^2)\) 的,但是考虑因为我们记录的 \((in,out)\) 对中 \((in,out)\) 一者一定是左子树或右子树中的一个点深度,又因为我们保留的 \(in\) 单增,\(out\) 单减,所有这样的 \((in,out)\) 最多只有 \(2\times light_i\) 对,其中 \(light_i\) 表示 \(i\) 的轻子树大小,所以复杂度是 \(O(\sum light_i)=O(n\log n)\),加上外层二分,若使用归并时间复杂度 \(O(n\log ^2n)\),直接 sort 三只 \(\log\) 也没啥问题。
这里是代码,实现使用了直接上传 vector 的做法,由于累计向父亲上传的大小之和仍然不大于轻子树大小,不会影响复杂度。
感觉这也不难啊为啥评了 *3900 .jpg
标签:子树,AGC007E,题解,复杂度,最大值,max,我们,out From: https://www.cnblogs.com/Dreamerkk/p/18101592