斜率优化&李超树

斜率优化dp

1. 写出dp方程，并让其变为线性

其中可能需要对性质的重要分析（难点）

式子一般长这个样

$$f(i)=min/max (h(j)+a(i)b(j)+g(i))$$

2. 模板化的，分离变量

具体的，先忽略 \(min/max\) （其实相当于选择一个最优的 \(j_0\)
）

$$f(i)=h(j_0)+a(i)b(j_0)+g(i)$$

把只与 \(j_0\) 相关的项放在一边，只与 \(i\) 相关的项放在另一边,既与 \(j_0\) 相关又与 \(i\) 相关的放在一起

$$h(j_0)=a(i)b(j_0)-f(i)+g(i)$$

其中设

$$Y=h(j_0),K=a(i),X=b(j_0),B=-f(i)+g(i)$$

（把 \(j\) 抽象成点 $ ( X(j),Y(j) ) $, \(i\) 抽象成直线 \(K(i)x+B(i)\) ）

则

$$Y(j)=K(i)X(j)+B(i)$$

若 \(K(x)\) 递增/递减，可以用单调队列（在队尾的斜率不达标的直接弹走）

若不行但 \(X(j)\) 单调 用二分

都不行，李超树（通解）

李超树

1. 完全体

link

要求在平面直角坐标系下维护两个操作：

1. 加入一个一次函数，定义域为 \([l,r]\) ；

2. 给定 \(k\) ，求定义域包含 \(k\) 的所有一次函数中，在 \(x=k\) 处取值最大的那个，如果有多个函数取值相同，选编号最小的。

warning 1

当线段垂直于 \(x\) 轴时，会出现除以零的情况。假设线段两端点分别为 \((x,y_0\) 和 \((x,y_1)\) ， \(y_0<y_1]\) ，则插入定义域为 \([x,x]\) 的一次函数 \(f(x)=0\cdot x+y_1\) 。

思想

按照线段树解决区间问题的常见方法，给每个节点一个懒标记。每个节点 \(i\) 的懒标记都是一条线段，记为 \(g_i\) 。

修改

考虑插入一条线段 \(g\) ，考虑左右端点恰好与 \(g\) 相同的的区间。若该区间无标记，直接打上用该线段更新的标记。

如果该区间已经有标记了，由于标记难以合并，只能标记永久化，把标记下传。但是子节点也有自己的标记，也可能产生冲突，所以我们要递归下传标记。

设当前区间的中点为 \(m\) ，我们拿新线段 \(g\) 在中点处的值与原最优线段 \(f\) 在中点处的值作比较。

如果新线段 \(g\) 更优，则将 \(g\) 和 \(f\) 交换。那么现在考虑在中点处 \(g\) 不如 \(f\) 优的情况：

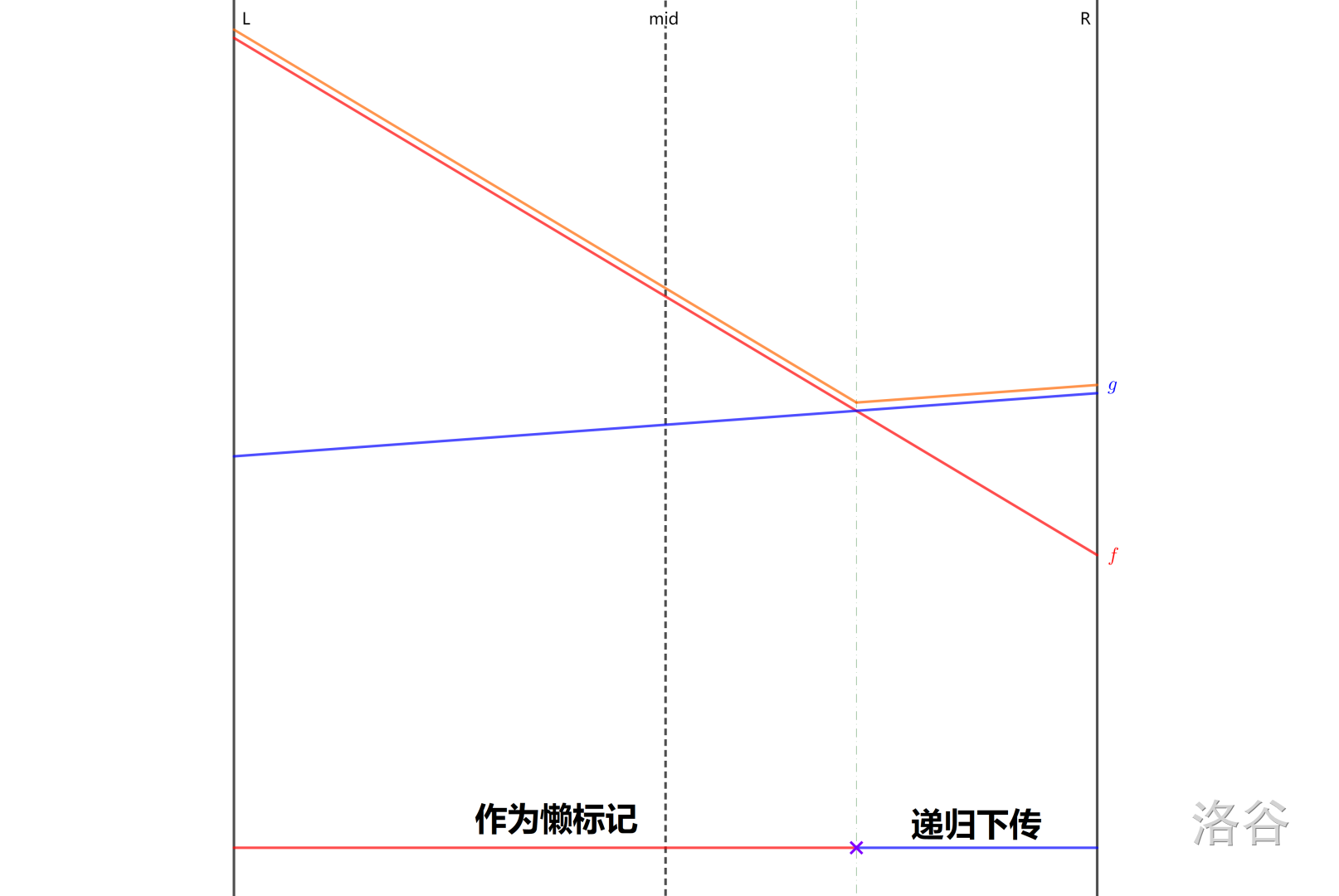
1. 若在左端点处 \(g\) 更优，那么 \(g\) 和 \(f\) 必然在左半区间中产生了交点， \(g\) 只有在左区间才可能优于 \(f\) ，递归到左儿子中进行下传；

2. 若在右端点处 \(g\) 更优，那么 \(g\) 和 \(f\) 必然在右半区间中产生了交点， \(g\) 只有在右区间才可能优于 \(f\) ，递归到右儿子中进行下传；

3. 若在左右端点处 \(f\) 都更优，那么 \(g\) 不可能成为答案，不需要继续下传。

除了这两种情况之外，还有一种情况是 \(g\) 和 \(f\) 刚好交于中点，在程序实现时可以归入中点处 \(g\) 不如 \(f\) 优的情况，结果会往 \(g\) 更优的一个端点进行递归下传。

最后将 \(f\) 作为当前区间的懒标记。

这样可以在 \(O(\log^2 n)\) 完成修改(一个线段最多分成 \(logn\) 个区间，每个修改最多 \(logn\) 次)

查询

如图所示，由于使用了标记永久化，懒标记并不等价于在区间中点处取值最大的线段。

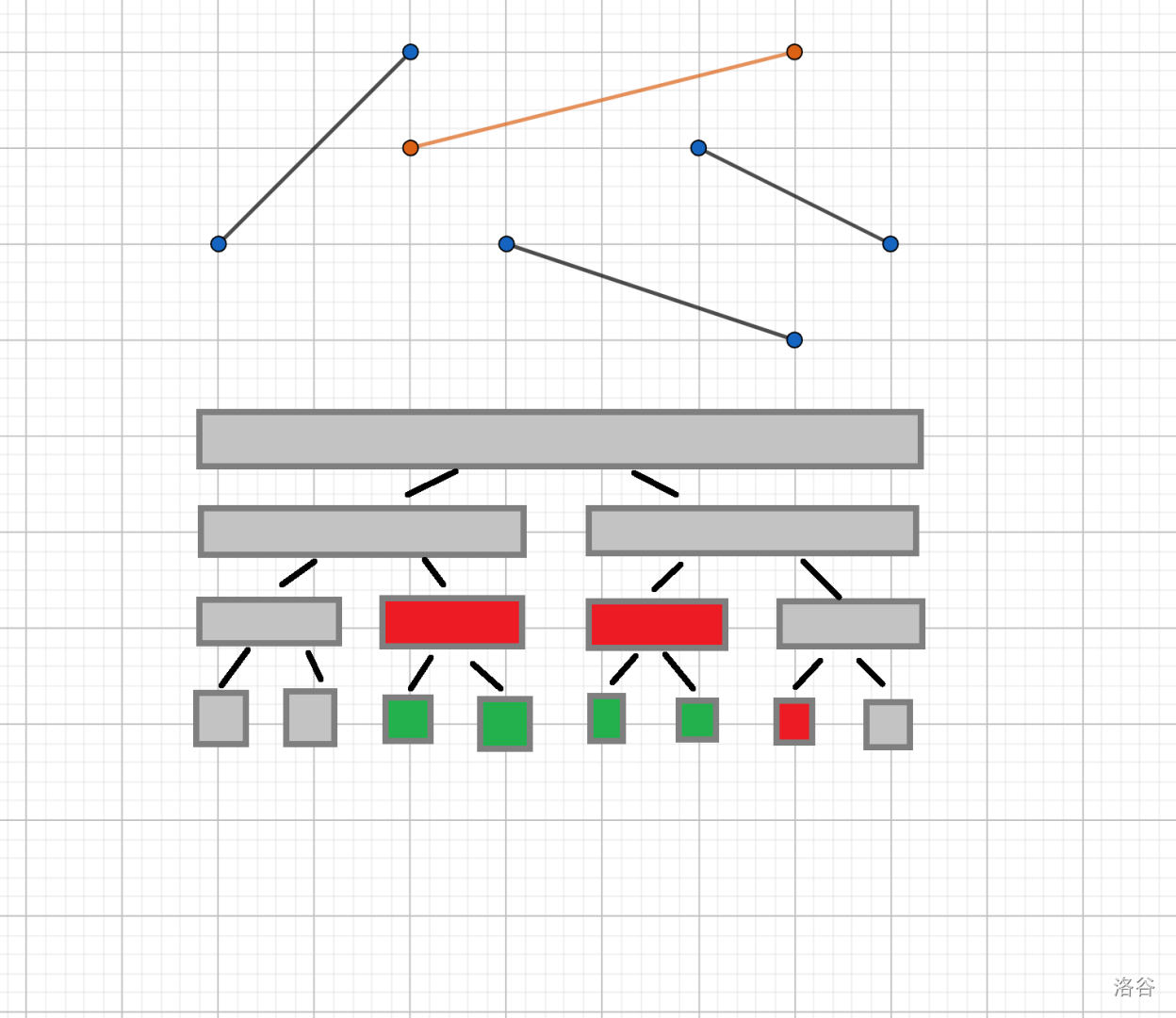
因此在查询时，在包含 \(x\) 的所有线段树区间（不超过 \(O(\log n)\) 个）的标记线段中取最值，得出最终答案。

code

warning 2

有时 \(x\) 的范围过大或不为整数 ( 货币兑换 ），无法直接作为下标，可以对其离散化之后再处理

2. only直线

这其实是更常见的一种情况，大部分题目(斜优)都对定义域没有要求。

当然，依然可以通过插入定义域为全体的线段来解决，但是太过于麻烦，这里提供一种简单，常数小的实现。

修改

1. 拿新线段 \(g\) 在中点处的值与原最优线段 \(f\) 在中点处的值作比较，决定要不要交换。

2. 若 \(g\) 的斜率大于 \(f\) 的斜率，在右儿子下传 \(g\)，否则在左儿子下传(可以由函数 \(g - f\) 的单调性得出)。

（还是可以看这个图理解，\(g\) 的斜率大于 \(f\) 的斜率）

这样可以在 \(O(logn)\) 的复杂度内解决

查询

直接以当前线段在 \(x\) 位置的值与左/右儿子其中之一的值取最大/最小值即可，复杂度 \(O(logn)\)

plus part李超树&斜优

对于李超树，不需要考虑单调性。但 \(i\) 与 \(j\) 的地位颠倒。

对于

$$f(i)=h(j)+a(i)b(j)+g(i)$$

分离 \(i\) 和 \(j\) ,但把 \(i\) 抽象成点 $ ( X(i),Y(i) ) $, \(j\) 抽象成直线 \(k(j)x+b(j)\)

即

$$f(i)-g(i)=a(i)b(j)+h(j)$$

其中设

$$Y=f(i)-g(i),K=b(j),X=a(i),B=h(j)$$

则有

$$Y(i)=K(j)X(i)+B(j)$$

每次在李超树里查询横坐标为 \(X(i)\) 的最大/小值，然后得到 \(f(i)=Y+g(i)\) ，再将 \(y=K(i)x+B(i)\) 插入即可