六、使用神经网络拟合数据
本章内容包括
-
与线性模型相比,非线性激活函数是关键区别
-
使用 PyTorch 的
nn模块 -
使用神经网络解决线性拟合问题
到目前为止,我们已经仔细研究了线性模型如何学习以及如何在 PyTorch 中实现这一点。我们专注于一个非常简单的回归问题,使用了一个只有一个输入和一个输出的线性模型。这样一个简单的例子使我们能够剖析一个学习模型的机制,而不会过于分散注意力于模型本身的实现。正如我们在第五章概述图中看到的,图 5.2(这里重复为图 6.1),了解训练模型的高级过程并不需要模型的确切细节。通过将错误反向传播到参数,然后通过对损失的梯度更新这些参数,无论底层模型是什么,这个过程都是相同的。
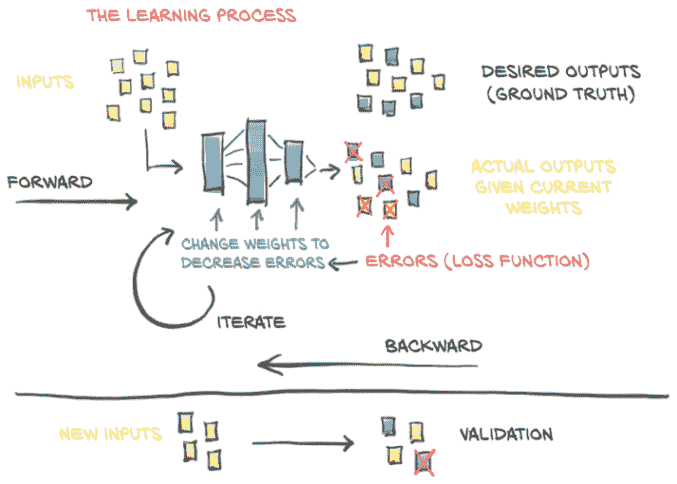
图 6.1 我们在第五章中实现的学习过程的心理模型
在本章中,我们将对我们的模型架构进行一些更改:我们将实现一个完整的人工神经网络来解决我们的温度转换问题。我们将继续使用上一章的训练循环,以及我们将华氏度转换为摄氏度的样本分为训练集和验证集。我们可以开始使用一个二次模型:将model重写为其输入的二次函数(例如,y = a * x**2 + b * x + c)。由于这样的模型是可微的,PyTorch 会负责计算梯度,训练循环将像往常一样工作。然而,对我们来说这并不是太有趣,因为我们仍然会固定函数的形状。
这是我们开始将我们的基础工作和您在项目中每天使用的 PyTorch 功能连接在一起的章节。您将了解 PyTorch API 背后的工作原理,而不仅仅是黑魔法。然而,在我们进入新模型的实现之前,让我们先了解一下人工神经网络的含义。
6.1 人工神经元
深度学习的核心是神经网络:能够通过简单函数的组合表示复杂函数的数学实体。术语神经网络显然暗示了与我们大脑工作方式的联系。事实上,尽管最初的模型受到神经科学的启发,现代人工神经网络与大脑中神经元的机制几乎没有相似之处。人工和生理神经网络似乎使用了略有相似的数学策略来逼近复杂函数,因为这类策略非常有效。
注意 从现在开始,我们将放弃人工这个词,将这些构造称为神经网络。
这些复杂函数的基本构建块是神经元,如图 6.2 所示。在其核心,它只是输入的线性变换(例如,将输入乘以一个数字[权重]并加上一个常数[偏置])后跟一个固定的非线性函数(称为*激活函数)。
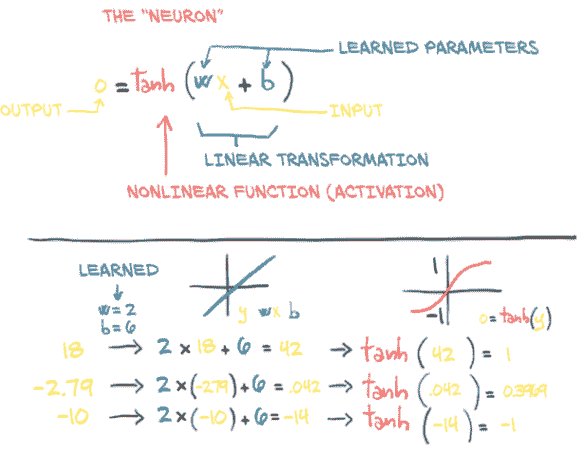
图 6.2 人工神经元:包含在非线性函数中的线性变换
从数学上讲,我们可以将其写为o = f(w * x + b),其中x是我们的输入,w是我们的权重或缩放因子,b是我们的偏置或偏移。f是我们的激活函数,这里设置为双曲正切函数,或者tan函数。一般来说,x和因此o可以是简单的标量,或者是矢量值(表示许多标量值);类似地,w可以是单个标量或矩阵,而b是标量或矢量(然而,输入和权重的维度必须匹配)。在后一种情况下,前面的表达式被称为一个神经元层,因为它通过多维权重和偏置表示许多神经元。
6.1.1 组合多层网络
如图 6.3 所示,一个多层神经网络由我们刚刚讨论的函数组合而成
x_1 = f(w_0 * x + b_0)
x_2 = f(w_1 * x_1 + b_1)
...
y = f(w_n * x_n + b_n)
神经元层的输出被用作下一层的输入。请记住,这里的w_0是一个矩阵,而x是一个向量!使用向量允许w_0保存整个层的神经元,而不仅仅是一个单独的权重。
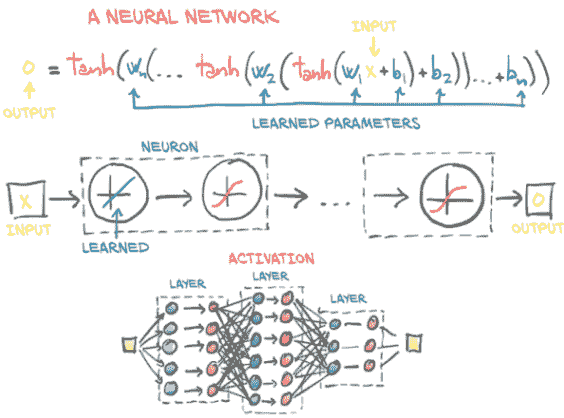
图 6.3 一个具有三层的神经网络
6.1.2 理解误差函数
我们之前的线性模型和我们实际用于深度学习的模型之间的一个重要区别是误差函数的形状。我们的线性模型和误差平方损失函数具有凸误差曲线,具有一个明确定义的最小值。如果我们使用其他方法,我们可以自动和明确地解决最小化误差函数的参数。这意味着我们的参数更新试图估计那个明确的正确答案。
即使使用相同的误差平方损失函数,神经网络也不具有凸误差曲面的属性!对于我们试图逼近的每个参数,没有一个单一的正确答案。相反,我们试图让所有参数在协同作用下产生一个有用的输出。由于这个有用的输出只会近似真相,所以会有一定程度的不完美。不完美会在何处和如何显现在某种程度上是任意的,因此控制输出(因此也是不完美)的参数也是任意的。这导致神经网络训练在机械角度上看起来非常像参数估计,但我们必须记住理论基础是完全不同的。
神经网络具有非凸误差曲面的一个重要原因是激活函数。一组神经元能够逼近非常广泛的有用函数的能力取决于每个神经元固有的线性和非线性行为的组合。
6.1.3 我们只需要激活
正如我们所看到的,(深度)神经网络中最简单的单元是线性操作(缩放 + 偏移)后跟一个激活函数。我们在我们最新的模型中已经有了我们的线性操作--线性操作就是整个模型。激活函数发挥着两个重要的作用:
-
在模型的内部部分,它允许输出函数在不同值处具有不同的斜率--这是线性函数根据定义无法做到的。通过巧妙地组合这些具有不同斜率的部分来产生许多输出,神经网络可以逼近任意函数,正如我们将在第 6.1.6 节中看到的。
-
在网络的最后一层,它的作用是将前面的线性操作的输出集中到给定范围内。
让我们谈谈第二点的含义。假设我们正在为图像分配“好狗狗”分数。金毛猎犬和西班牙猎犬的图片应该有一个高分,而飞机和垃圾车的图片应该有一个低分。熊的图片也应该有一个较低的分数,尽管比垃圾车高。
问题在于,我们必须定义一个“高分”:我们有整个float32范围可供使用,这意味着我们可以得到相当高的分数。即使我们说“这是一个 10 分制”,仍然存在一个问题,即有时我们的模型会产生 11 分中的 11 分。请记住,在底层,这都是(w*x+b)矩阵乘法的总和,它们不会自然地限制自己在特定范围的输出。
限制输出范围
我们希望牢固地约束我们线性操作的输出到特定范围,这样输出的消费者就不必处理小狗得分为 12/10,熊得分为-10,垃圾车得分为-1,000 的数值输入。
一种可能性是简单地限制输出数值:低于 0 的设为 0,高于 10 的设为 10。这是一个简单的激活函数称为torch.nn.Hardtanh(pytorch.org/docs/stable/nn.html#hardtanh,但请注意默认范围是-1 到+1)。
压缩输出范围
另一组效果良好的函数是torch.nn.Sigmoid,其中包括1 / (1 + e ** -x),torch.tanh,以及我们马上会看到的其他函数。这些函数的曲线在x趋于负无穷时渐近地接近 0 或-1,在x增加时接近 1,并且在x == 0时具有大致恒定的斜率。从概念上讲,这种形状的函数效果很好,因为我们线性函数输出的中间区域是我们的神经元(再次强调,这只是一个线性函数后跟一个激活函数)会敏感的区域,而其他所有内容都被归类到边界值旁边。正如我们在图 6.4 中看到的,我们的垃圾车得分为-0.97,而熊、狐狸和狼的得分则在-0.3 到 0.3 的范围内。
这导致垃圾车被标记为“不是狗”,我们的好狗被映射为“明显是狗”,而我们的熊则处于中间位置。在代码中,我们可以看到确切的数值:
>>> import math
>>> math.tanh(-2.2) # ❶
-0.9757431300314515
>>> math.tanh(0.1) # ❷
0.09966799462495582
>>> math.tanh(2.5) # ❸
0.9866142981514303
❶ 垃圾车
❷ 熊
❸ 好狗狗
当熊处于敏感范围时,对熊进行微小的更改将导致结果明显变化。例如,我们可以从灰熊切换到北极熊(其面部略带更传统的犬类面孔),随着我们滑向图表“非常像狗”的一端,我们会看到Y轴上的跳跃。相反,考拉熊会被认为不太像狗,我们会看到激活输出下降。然而,我们几乎无法让垃圾车被认为像狗:即使进行 drastical 改变,我们可能只会看到从-0.97 到-0.8 左右的变化。

图 6.4 显示了狗、熊和垃圾车通过tanh激活函数映射为它们的狗样程度
6.1.4 更多激活函数
有许多激活函数,其中一些显示在图 6.5 中。在第一列中,我们看到平滑函数Tanh和Softplus,而第二列有激活函数的“硬”版本:Hardtanh和ReLU。ReLU(修正线性单元)值得特别注意,因为它目前被认为是表现最佳的通用激活函数之一;许多最新技术的结果都使用了它。Sigmoid激活函数,也称为逻辑函数,在早期深度学习工作中被广泛使用,但自那时以来已经不再常用,除非我们明确希望将其移动到 0...1 范围内:例如,当输出应该是概率时。最后,LeakyReLU函数修改了标准的ReLU,使其具有小的正斜率,而不是对负输入严格为零(通常这个斜率为 0.01,但这里显示为 0.1 以便清楚显示)。
6.1.5 选择最佳激活函数
激活函数很奇特,因为有许多被证明成功的种类(远远不止图 6.5 中显示的),很明显几乎没有严格的要求。因此,我们将讨论一些关于激活函数的一般性,这些一般性可能在具体情况下很容易被证伪。也就是说,根据定义,激活函数
-
是非线性的。重复应用(
w*x+b)而没有激活函数会导致具有相同(仿射线性)形式的函数。非线性允许整个网络逼近更复杂的函数。 -
是可微的,因此可以通过它们计算梯度。像
Hardtanh或ReLU中看到的点间断是可以接受的。
没有这些特征,网络要么退回成为线性模型,要么变得难以训练。
以下对这些函数是正确的:
-
它们至少有一个敏感范围,在这个范围内对输入进行非平凡的更改会导致相应的输出发生非平凡的变化。这对于训练是必要的。
-
许多激活函数具有不敏感(或饱和)范围,在这个范围内对输入进行更改几乎不会对输出产生任何或很少的变化。
举例来说,Hardtanh函数可以通过在输入上组合敏感范围与不同的权重和偏置来轻松地用于制作函数的分段线性逼近。

图 6.5 常见和不那么常见的激活函数集合
通常(但远非普遍如此),激活函数至少具有以下之一:
-
一个下界,当输入趋于负无穷时接近(或达到)
-
一个类似但相反的正无穷的上界
想想我们对反向传播如何工作的了解,我们可以得出结论,当输入处于响应范围时,错误将通过激活向后传播得更有效,而当输入饱和时,错误不会对神经元产生很大影响(因为梯度将接近于零,由于输出周围的平坦区域)。
将所有这些放在一起,这就产生了一个非常强大的机制:我们在说,当将不同的输入呈现给由线性 + 激活单元构建的网络时,(a)不同的单元将对相同的输入在不同的范围内做出响应,而(b)与这些输入相关的错误主要会影响在敏感范围内运行的神经元,使其他单元在学习过程中基本上不受影响。此外,由于激活函数相对于其输入的导数在敏感范围内通常接近于 1,通过梯度下降估计在该范围内运行的单元的线性变换的参数将看起来很像我们之前看到的线性拟合。
我们开始对如何将许多线性 + 激活单元并行连接并依次堆叠起来形成一个能够逼近复杂函数的数学对象有了更深入的直觉。不同的单元组合将对输入在不同的范围内做出响应,并且这些单元的参数相对容易通过梯度下降进行优化,因为学习过程将表现得很像线性函数直到输出饱和。
6.1.6 神经网络的学习意味着什么
通过堆叠线性变换和可微激活函数构建模型,可以得到能够近似高度非线性过程的模型,并且我们可以通过梯度下降方法出奇地好地估计其参数。即使处理具有数百万参数的模型时,这仍然成立。使用深度神经网络如此吸引人的原因在于,它使我们不必过多担心代表我们数据的确切函数--无论是二次的、分段多项式的,还是其他什么。通过深度神经网络模型,我们有一个通用的逼近器和一个估计其参数的方法。这个逼近器可以根据我们的需求进行定制,无论是模型容量还是模型复杂输入/输出关系的能力,只需组合简单的构建块。我们可以在图 6.6 中看到一些例子。

图 6.6 组合多个线性单元和tanh激活函数以产生非线性输出
四个左上角的图显示了四个神经元--A、B、C 和 D--每个都有自己(任意选择的)权重和偏置。每个神经元使用Tanh激活函数,最小值为-1,最大值为 1。不同的权重和偏置移动了中心点,并改变了从最小到最大的过渡有多么剧烈,但它们显然都有相同的一般形状。在这些右侧的列中,显示了两对神经元相加在一起(A + B,然后是 C + D)。在这里,我们开始看到一些模仿单层神经元的有趣特性。A + B 显示了一个轻微的S曲线,极端值接近 0,但中间有一个正峰和一个负峰。相反,C + D 只有一个大的正峰,峰值高于我们单个神经元的最大值 1。
在第三行,我们开始组合我们的神经元,就像它们在一个两层网络中的样子。C(A + B)和 D(A + B)都有与 A + B 相同的正负峰,但正峰更加微妙。C(A + B) + D(A + B)的组合显示了一个新的特性:两个明显的负峰,可能还有一个非常微妙的第二个正峰,位于主要感兴趣区域的左侧。所有这些只用了两层中的四个神经元!
再次强调,这些神经元的参数仅仅是为了得到一个视觉上有趣的结果而选择的。训练的过程是找到这些权重和偏置的可接受值,使得最终的网络能够正确执行任务,比如根据地理坐标和年份时间预测可能的温度。通过成功执行任务,我们指的是在由用于训练数据的相同数据生成过程产生的未见数据上获得正确的输出。一个成功训练的网络,通过其权重和偏置的值,将以有意义的数字表示形式捕捉数据的固有结构,这些数字表示对以前未见的数据能够正确工作。
让我们在了解学习机制方面再迈出一步:深度神经网络使我们能够近似高度非线性的现象,而无需为其建立明确的模型。相反,从一个通用的、未经训练的模型开始,我们通过提供一组输入和输出以及一个损失函数来专门针对一个任务进行特化,并通过反向传播来优化。通过示例将通用模型专门化到一个任务上,这就是我们所说的学习,因为该模型并不是为特定任务而构建的--没有规则描述该任务如何工作被编码在模型中。
对于我们的温度计示例,我们假设两个温度计都是线性测量温度的。这个假设是我们隐式编码任务规则的地方:我们硬编码了输入/输出函数的形状;我们无法逼近除了围绕一条直线的数据点之外的任何东西。随着问题的维度增加(即,许多输入到许多输出)和输入/输出关系变得复杂,假设输入/输出函数的形状不太可能奏效。物理学家或应用数学家的工作通常是从第一原理提出现象的功能性描述,这样我们就可以从测量中估计未知参数,并获得对世界的准确模型。另一方面,深度神经网络是一类函数族,具有近似各种输入/输出关系的能力,而不一定需要我们提出现象的解释模型。在某种程度上,我们放弃了解释,以换取解决日益复杂问题的可能性。另一方面,我们有时缺乏建立我们所面对的事物的显式模型的能力、信息或计算资源,因此数据驱动的方法是我们前进的唯一途径。
6.2 PyTorch nn 模块
所有这些关于神经网络的讨论可能让您对使用 PyTorch 从头开始构建一个神经网络感到非常好奇。我们的第一步将是用一个神经网络单元替换我们的线性模型。从正确性的角度来看,这将是一个有点无用的后退,因为我们已经验证了我们的校准只需要一个线性函数,但从足够简单的问题开始并随后扩展仍然是非常重要的。
PyTorch 有一个专门用于神经网络的子模块,称为torch.nn。它包含创建各种神经网络架构所需的构建模块。在 PyTorch 的术语中,这些构建模块称为模块(在其他框架中,这些构建模块通常被称为层)。PyTorch 模块是从nn.Module基类派生的 Python 类。一个模块可以有一个或多个Parameter实例作为属性,这些张量的值在训练过程中进行优化(想想我们线性模型中的w和b)。一个模块也可以有一个或多个子模块(nn.Module的子类)作为属性,并且它将能够跟踪它们的参数。
注意 子模块必须是顶级属性,而不是嵌套在list或dict实例中!否则,优化器将无法定位子模块(因此也无法定位它们的参数)。对于您的模型需要子模块列表或字典的情况,PyTorch 提供了nn.ModuleList和nn.ModuleDict。
毫不奇怪,我们可以找到一个名为nn.Linear的nn.Module子类,它对其输入应用一个仿射变换(通过参数属性weight和bias)并等同于我们在温度计实验中早期实现的内容。我们现在将从我们离开的地方精确开始,并将我们以前的代码转换为使用nn的形式。
6.2.1 使用 call 而不是 forward
所有 PyTorch 提供的nn.Module的子类都定义了它们的__call__方法。这使我们能够实例化一个nn.Linear并将其调用为一个函数,就像这样(代码/p1ch6/1_neural_networks.ipynb):
# In[5]:
import torch.nn as nn
linear_model = nn.Linear(1, 1) # ❶
linear_model(t_un_val)
# Out[5]:
tensor([[0.6018],
[0.2877]], grad_fn=<AddmmBackward>)
❶ 我们马上会看构造函数参数。
使用一组参数调用nn.Module的实例最终会调用一个名为forward的方法,该方法使用相同的参数。forward方法执行前向计算,而__call__在调用forward之前和之后执行其他相当重要的任务。因此,从技术上讲,可以直接调用forward,它将产生与__call__相同的输出,但不应该从用户代码中这样做:
y = model(x) # ❶
y = model.forward(x) # ❷
❶ 正确!
❷ 沉默的错误。不要这样做!
这是 Module._call_ 的实现(我们省略了与 JIT 相关的部分,并对清晰起见进行了一些简化;torch/nn/modules/module.py,第 483 行,类:Module):
def __call__(self, *input, **kwargs):
for hook in self._forward_pre_hooks.values():
hook(self, input)
result = self.forward(*input, **kwargs)
for hook in self._forward_hooks.values():
hook_result = hook(self, input, result)
# ...
for hook in self._backward_hooks.values():
# ...
return result
正如我们所看到的,如果我们直接使用 .forward(...),将无法正确调用许多钩子。
6.2.2 返回线性模型
回到我们的线性模型。nn.Linear 的构造函数接受三个参数:输入特征的数量、输出特征的数量,以及线性模型是否包括偏置(默认为 True):
# In[5]:
import torch.nn as nn
linear_model = nn.Linear(1, 1) # ❶
linear_model(t_un_val)
# Out[5]:
tensor([[0.6018],
[0.2877]], grad_fn=<AddmmBackward>)
❶ 参数是输入大小、输出大小和默认为 True 的偏置。
在我们的情况中,特征的数量只是指模块的输入和输出张量的大小,因此为 1 和 1。例如,如果我们将温度和气压作为输入,那么输入中将有两个特征,输出中将有一个特征。正如我们将看到的,对于具有多个中间模块的更复杂模型,特征的数量将与模型的容量相关联。
我们有一个具有一个输入和一个输出特征的 nn.Linear 实例。这只需要一个权重和一个偏置:
# In[6]:
linear_model.weight
# Out[6]:
Parameter containing:
tensor([[-0.0674]], requires_grad=True)
# In[7]:
linear_model.bias
# Out[7]:
Parameter containing:
tensor([0.7488], requires_grad=True)
我们可以使用一些输入调用该模块:
# In[8]:
x = torch.ones(1)
linear_model(x)
# Out[8]:
tensor([0.6814], grad_fn=<AddBackward0>)
尽管 PyTorch 让我们可以这样做,但实际上我们并没有提供正确维度的输入。我们有一个接受一个输入并产生一个输出的模型,但 PyTorch 的 nn.Module 及其子类是设计用于同时处理多个样本的。为了容纳多个样本,模块期望输入的零维是批次中的样本数量。我们在第四章遇到过这个概念,当时我们学习如何将现实世界的数据排列成张量。
批处理输入
nn 中的任何模块都是为了一次对批量中的多个输入产生输出而编写的。因此,假设我们需要在 10 个样本上运行 nn.Linear,我们可以创建一个大小为 B × Nin 的输入张量,其中 B 是批次的大小,Nin 是输入特征的数量,并将其一次通过模型运行。例如:
# In[9]:
x = torch.ones(10, 1)
linear_model(x)
# Out[9]:
tensor([[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814],
[0.6814]], grad_fn=<AddmmBackward>)
让我们深入研究一下这里发生的情况,图 6.7 显示了批处理图像数据的类似情况。我们的输入是 B × C × H × W,批处理大小为 3(比如,一只狗、一只鸟和一辆车的图像),三个通道维度(红色、绿色和蓝色),以及高度和宽度的未指定像素数量。正如我们所看到的,输出是大小为 B × Nout 的张量,其中 Nout 是输出特征的数量:在这种情况下是四个。
优化批处理
我们希望进行批处理的原因是多方面的。一个重要的动机是确保我们请求的计算量足够大,以充分利用我们用来执行计算的计算资源。特别是 GPU 是高度并行化的,因此在小型模型上单个输入会使大多数计算单元处于空闲状态。通过提供输入的批处理,计算可以分布在否则空闲的单元上,这意味着批处理结果会像单个结果一样快速返回。另一个好处是一些高级模型使用整个批次的统计信息,这些统计信息随着批次大小的增加而变得更好。

图 6.7 三个 RGB 图像一起批处理并输入到神经网络中。输出是大小为 4 的三个向量的批处理结果。
回到我们的温度计数据,t_u 和 t_c 是大小为 B 的两个 1D 张量。借助广播,我们可以将我们的线性模型写成 w * x + b,其中 w 和 b 是两个标量参数。这是因为我们只有一个输入特征:如果有两个,我们需要添加一个额外维度,将该 1D 张量转换为一个矩阵,其中行中有样本,列中有特征。
这正是我们需要做的,以切换到使用 nn.Linear。我们将我们的 B 输入重塑为 B × Nin,其中 Nin 为 1。这可以很容易地通过 unsqueeze 完成:
# In[2]:
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # ❶
t_u = torch.tensor(t_u).unsqueeze(1) # ❶
t_u.shape
# Out[2]:
torch.Size([11, 1])
❶ 在轴 1 处添加额外维度
我们完成了;让我们更新我们的训练代码。首先,我们用nn.Linear(1,1)替换我们手工制作的模型,然后我们需要将线性模型的参数传递给优化器:
# In[10]:
linear_model = nn.Linear(1, 1) # ❶
optimizer = optim.SGD(
linear_model.parameters(), # ❷
lr=1e-2)
❶ 这只是之前的重新定义。
❷ 这个方法调用替换了[params]。
之前,我们的责任是创建参数并将它们作为optim.SGD的第一个参数传递。现在我们可以使用parameters方法向任何nn.Module询问由它或其任何子模块拥有的参数列表:
# In[11]:
linear_model.parameters()
# Out[11]:
<generator object Module.parameters at 0x7f94b4a8a750>
# In[12]:
list(linear_model.parameters())
# Out[12]:
[Parameter containing:
tensor([[0.7398]], requires_grad=True), Parameter containing:
tensor([0.7974], requires_grad=True)]
此调用递归地进入模块的init构造函数中定义的子模块,并返回遇到的所有参数的平面列表,这样我们就可以方便地将其传递给优化器构造函数,就像我们之前做的那样。
我们已经可以弄清楚训练循环中发生了什么。优化器提供了一个张量列表,这些张量被定义为requires_grad = True--所有的Parameter都是这样定义的,因为它们需要通过梯度下降进行优化。当调用training_loss.backward()时,grad会在图的叶节点上累积,这些叶节点恰好是传递给优化器的参数。
此时,SGD 优化器已经拥有了一切所需的东西。当调用optimizer.step()时,它将遍历每个Parameter,并按照其grad属性中存储的量进行更改。设计相当干净。
现在让我们看一下训练循环:
# In[13]:
def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,
t_c_train, t_c_val):
for epoch in range(1, n_epochs + 1):
t_p_train = model(t_u_train) # ❶
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val) # ❶
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward() # ❷
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
f" Validation loss {loss_val.item():.4f}")
❶ 现在传入的是模型,而不是单独的参数。
❷ 损失函数也被传入。我们马上会用到它。
实际上几乎没有任何变化,只是现在我们不再显式地将params传递给model,因为模型本身在内部保存了它的Parameters。
还有最后一点,我们可以从torch.nn中利用的:损失。确实,nn带有几种常见的损失函数,其中包括nn.MSELoss(MSE 代表均方误差),这正是我们之前定义的loss_fn。nn中的损失函数仍然是nn.Module的子类,因此我们将创建一个实例并将其作为函数调用。在我们的情况下,我们摆脱了手写的loss_fn并替换它:
# In[15]:
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
training_loop(
n_epochs = 3000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(), # ❶
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)
print()
print(linear_model.weight)
print(linear_model.bias)
# Out[15]:
Epoch 1, Training loss 134.9599, Validation loss 183.1707
Epoch 1000, Training loss 4.8053, Validation loss 4.7307
Epoch 2000, Training loss 3.0285, Validation loss 3.0889
Epoch 3000, Training loss 2.8569, Validation loss 3.9105
Parameter containing:
tensor([[5.4319]], requires_grad=True)
Parameter containing:
tensor([-17.9693], requires_grad=True)
❶ 我们不再使用之前手写的损失函数。
所有输入到我们的训练循环中的其他内容保持不变。即使我们的结果仍然与以前相同。当然,得到相同的结果是预期的,因为任何差异都意味着两种实现中的一个存在错误。
6.3 最后是神经网络
这是一个漫长的旅程--这 20 多行代码中有很多可以探索的内容,我们需要定义和训练一个模型。希望到现在为止,训练中涉及的魔法已经消失,为机械留下了空间。到目前为止我们学到的东西将使我们能够拥有我们编写的代码,而不仅仅是在事情变得更加复杂时摸黑箱。
还有最后一步要走:用神经网络替换我们的线性模型作为我们的逼近函数。我们之前说过,使用神经网络不会导致更高质量的模型,因为我们校准问题的过程基本上是线性的。然而,在受控环境中从线性到神经网络的跃迁是有好处的,这样我们以后就不会感到迷失。
6.3.1 替换线性模型
我们将保持其他所有内容不变,包括损失函数,并且只重新定义model。让我们构建可能的最简单的神经网络:一个线性模块,后跟一个激活函数,进入另一个线性模块。第一个线性 + 激活层通常被称为隐藏层,出于历史原因,因为它的输出不是直接观察到的,而是馈送到输出层。虽然模型的输入和输出都是大小为 1(它们具有一个输入和一个输出特征),但第一个线性模块的输出大小通常大于 1。回顾我们之前对激活作用的解释,这可以导致不同的单元对输入的不同范围做出响应,从而增加我们模型的容量。最后一个线性层将获取激活的输出,并将它们线性组合以产生输出值。
没有标准的神经网络表示方法。图 6.8 显示了两种似乎有些典型的方式:左侧显示了我们的网络可能在基本介绍中如何描述,而右侧类似于更高级文献和研究论文中经常使用的风格。通常制作大致对应于 PyTorch 提供的神经网络模块的图块(尽管有时像Tanh激活层这样的东西并没有明确显示)。请注意,两者之间的一个略微微妙的区别是左侧的图中将输入和(中间)结果放在圆圈中作为主要元素。右侧,计算步骤更加突出。

图 6.8 我们最简单的神经网络的两个视图。左:初学者版本。右:高级版本。
nn通过nn.Sequential容器提供了一种简单的方法来连接模块:
# In[16]:
seq_model = nn.Sequential(
nn.Linear(1, 13), # ❶
nn.Tanh(),
nn.Linear(13, 1)) # ❷
seq_model
# Out[16]:
Sequential(
(0): Linear(in_features=1, out_features=13, bias=True)
(1): Tanh()
(2): Linear(in_features=13, out_features=1, bias=True)
)
❶ 我们随意选择了 13。我们希望这个数字与我们周围漂浮的其他张量形状大小不同。
❷ 这个 13 必须与第一个大小匹配。
最终结果是一个模型,它接受由nn.Sequential的第一个模块指定的输入,将中间输出传递给后续模块,并产生由最后一个模块返回的输出。该模型从 1 个输入特征扩展到 13 个隐藏特征,通过一个tanh激活,然后将产生的 13 个数字线性组合成 1 个输出特征。
6.3.2 检查参数
调用model.parameters()将收集第一个和第二个线性模块的weight和bias。在这种情况下通过打印它们的形状来检查参数是很有启发性的:
# In[17]:
[param.shape for param in seq_model.parameters()]
# Out[17]:
[torch.Size([13, 1]), torch.Size([13]), torch.Size([1, 13]), torch.Size([1])]
这些是优化器将获得的张量。再次,在我们调用model.backward()之后,所有参数都将填充其grad,然后优化器在optimizer.step()调用期间相应地更新它们的值。和我们之前的线性模型没有太大不同,对吧?毕竟,它们都是可以使用梯度下降进行训练的可微分模型。
有关nn.Modules参数的一些注意事项。当检查由几个子模块组成的模型的参数时,能够通过名称识别参数是很方便的。有一个方法可以做到这一点,称为named_parameters:
# In[18]:
for name, param in seq_model.named_parameters():
print(name, param.shape)
# Out[18]:
0.weight torch.Size([13, 1])
0.bias torch.Size([13])
2.weight torch.Size([1, 13])
2.bias torch.Size([1])
Sequential中每个模块的名称只是模块在参数中出现的顺序。有趣的是,Sequential还接受一个OrderedDict,在其中我们可以为传递给Sequential的每个模块命名:
# In[19]:
from collections import OrderedDict
seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 8)),
('hidden_activation', nn.Tanh()),
('output_linear', nn.Linear(8, 1))
]))
seq_model
# Out[19]:
Sequential(
(hidden_linear): Linear(in_features=1, out_features=8, bias=True)
(hidden_activation): Tanh()
(output_linear): Linear(in_features=8, out_features=1, bias=True)
)
这使我们可以为子模块获得更具解释性的名称:
# In[20]:
for name, param in seq_model.named_parameters():
print(name, param.shape)
# Out[20]:
hidden_linear.weight torch.Size([8, 1])
hidden_linear.bias torch.Size([8])
output_linear.weight torch.Size([1, 8])
output_linear.bias torch.Size([1])
这更具描述性;但它并没有给我们更多控制数据流的灵活性,数据流仍然是纯粹的顺序传递--nn.Sequential的命名非常贴切。我们将在第八章中看到如何通过自己子类化nn.Module来完全控制输入数据的处理。
我们还可以通过使用子模块作为属性来访问特定的Parameter:
# In[21]:
seq_model.output_linear.bias
# Out[21]:
Parameter containing:
tensor([-0.0173], requires_grad=True)
这对于检查参数或它们的梯度非常有用:例如,要监视训练过程中的梯度,就像我们在本章开头所做的那样。假设我们想要打印出隐藏层线性部分的weight的梯度。我们可以运行新神经网络模型的训练循环,然后在最后一个时期查看结果梯度:
# In[22]:
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3) # ❶
training_loop(
n_epochs = 5000,
optimizer = optimizer,
model = seq_model,
loss_fn = nn.MSELoss(),
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)
print('output', seq_model(t_un_val))
print('answer', t_c_val)
print('hidden', seq_model.hidden_linear.weight.grad)
# Out[22]:
Epoch 1, Training loss 182.9724, Validation loss 231.8708
Epoch 1000, Training loss 6.6642, Validation loss 3.7330
Epoch 2000, Training loss 5.1502, Validation loss 0.1406
Epoch 3000, Training loss 2.9653, Validation loss 1.0005
Epoch 4000, Training loss 2.2839, Validation loss 1.6580
Epoch 5000, Training loss 2.1141, Validation loss 2.0215
output tensor([[-1.9930],
[20.8729]], grad_fn=<AddmmBackward>)
answer tensor([[-4.],
[21.]])
hidden tensor([[ 0.0272],
[ 0.0139],
[ 0.1692],
[ 0.1735],
[-0.1697],
[ 0.1455],
[-0.0136],
[-0.0554]])
❶ 我们稍微降低了学习率以提高稳定性。
6.3.3 与线性模型比较
我们还可以评估模型在所有数据上的表现,并查看它与一条直线的差异:
# In[23]:
from matplotlib import pyplot as plt
t_range = torch.arange(20., 90.).unsqueeze(1)
fig = plt.figure(dpi=600)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
结果显示在图 6.9 中。我们可以看到神经网络有过拟合的倾向,正如我们在第五章讨论的那样,因为它试图追踪测量值,包括嘈杂的值。即使我们微小的神经网络有太多参数来拟合我们所拥有的少量测量值。总的来说,它做得还不错。

图 6.9 我们的神经网络模型的绘图,包括输入数据(圆圈)和模型输出(X)。连续线显示样本之间的行为。
6.4 结论
尽管我们一直在处理一个非常简单的问题,但在第五章和第六章中我们已经涵盖了很多内容。我们分析了构建可微分模型并使用梯度下降进行训练,首先使用原始自动求导,然后依赖于nn。到目前为止,您应该对幕后发生的事情有信心。希望这一次 PyTorch 的体验让您对更多内容感到兴奋!
6.5 练习
-
在我们简单的神经网络模型中尝试隐藏神经元的数量以及学习率。
-
什么改变会导致模型输出更线性?
-
你能明显地使模型过拟合数据吗?
-
-
物理学中第三难的问题是找到一种合适的葡萄酒来庆祝发现。从第四章加载葡萄酒数据,并创建一个具有适当数量输入参数的新模型。
-
训练所需时间与我们一直在使用的温度数据相比需要多长时间?
-
你能解释哪些因素导致训练时间?
-
你能在这个数据集上训练时使损失减少吗?
-
你会如何绘制多个数据集的图表?
-
6.6 总结
-
神经网络可以自动适应专门解决手头问题。
-
神经网络允许轻松访问模型中任何参数相对于损失的解析导数,这使得演化参数非常高效。由于其自动微分引擎,PyTorch 轻松提供这些导数。
-
环绕线性变换的激活函数使神经网络能够逼近高度非线性函数,同时保持足够简单以进行优化。
-
nn模块与张量标准库一起提供了创建神经网络的所有构建模块。 -
要识别过拟合,保持训练数据点与验证集分开是至关重要的。没有一种对抗过拟合的固定方法,但增加数据量,或增加数据的变化性,并转向更简单的模型是一个良好的开始。
-
做数据科学的人应该一直在绘制数据。
¹ 参见 F. Rosenblatt,“感知器:大脑中信息存储和组织的概率模型”,心理评论 65(6),386-408(1958 年),pubmed.ncbi.nlm.nih.gov/13602029/。
² 为了直观地理解这种通用逼近性质,你可以从图 6.5 中选择一个函数,然后构建一个几乎在大部分区域为零且在x = 0 周围为正的基本函数,通过缩放(包括乘以负数)、平移激活函数的副本。通过这个基本函数的缩放、平移和扩展(沿X轴挤压)的副本,你可以逼近任何(连续)函数。在图 6.6 中,右侧中间行的函数可能是这样一个基本构件。Michael Nielsen 在他的在线书籍神经网络与深度学习中有一个交互式演示,网址为mng.bz/Mdon。
³ 当然,即使这些说法并不总是正确;参见 Jakob Foerster 的文章,“深度线性网络中的非线性计算”,OpenAI,2019,mng.bz/gygE。
⁴ 并非所有版本的 Python 都指定了dict的迭代顺序,因此我们在这里使用OrderedDict来确保层的顺序,并强调层的顺序很重要。
七、从图像中识别鸟类和飞机:从图像中学习
本章内容包括
-
构建前馈神经网络
-
使用
Dataset和DataLoader加载数据 -
理解分类损失
上一章让我们有机会深入了解通过梯度下降学习的内部机制,以及 PyTorch 提供的构建模型和优化模型的工具。我们使用了一个简单的具有一个输入和一个输出的回归模型,这使我们可以一目了然,但诚实地说只是勉强令人兴奋。
在本章中,我们将继续构建我们的神经网络基础。这一次,我们将把注意力转向图像。图像识别可以说是让世界意识到深度学习潜力的任务。
我们将逐步解决一个简单的图像识别问题,从上一章中定义的简单神经网络开始构建。这一次,我们将使用一个更广泛的小图像数据集,而不是一组数字。让我们首先下载数据集,然后开始准备使用它。
7.1 一个小图像数据集
没有什么比对一个主题的直观理解更好,也没有什么比处理简单数据更能实现这一点。图像识别中最基本的数据集之一是被称为 MNIST 的手写数字识别数据集。在这里,我们将使用另一个类似简单且更有趣的数据集。它被称为 CIFAR-10,就像它的姐妹 CIFAR-100 一样,它已经成为计算机视觉领域的经典数据集十年。
CIFAR-10 由 60,000 个 32×32 彩色(RGB)图像组成,标记为 10 个类别中的一个整数:飞机(0)、汽车(1)、鸟(2)、猫(3)、鹿(4)、狗(5)、青蛙(6)、马(7)、船(8)和卡车(9)。如今,CIFAR-10 被认为对于开发或验证新研究来说过于简单,但对于我们的学习目的来说完全够用。我们将使用torchvision模块自动下载数据集,并将其加载为一组 PyTorch 张量。图 7.1 让我们一睹 CIFAR-10 的风采。

图 7.1 显示所有 CIFAR-10 类别的图像样本
7.1.1 下载 CIFAR-10
正如我们预期的那样,让我们导入torchvision并使用datasets模块下载 CIFAR-10 数据:
# In[2]:
from torchvision import datasets
data_path = '../data-unversioned/p1ch7/'
cifar10 = datasets.CIFAR10(data_path, train=True, download=True) # ❶
cifar10_val = datasets.CIFAR10(data_path, train=False, download=True) # ❷
❶ 为训练数据实例化一个数据集;如果数据不存在,TorchVision 会下载数据
❷ 使用 train=False,这样我们就得到了一个用于验证数据的数据集,如果需要的话会进行下载。
我们提供给CIFAR10函数的第一个参数是数据将被下载的位置;第二个参数指定我们是对训练集感兴趣还是对验证集感兴趣;第三个参数表示我们是否允许 PyTorch 在指定的位置找不到数据时下载数据。
就像CIFAR10一样,datasets子模块为我们提供了对最流行的计算机视觉数据集的预先访问,如 MNIST、Fashion-MNIST、CIFAR-100、SVHN、Coco 和 Omniglot。在每种情况下,数据集都作为torch.utils.data.Dataset的子类返回。我们可以看到我们的cifar10实例的方法解析顺序将其作为一个基类:
# In[4]:
type(cifar10).__mro__
# Out[4]:
(torchvision.datasets.cifar.CIFAR10,
torchvision.datasets.vision.VisionDataset,
torch.utils.data.dataset.Dataset,
object)
7.1.2 Dataset 类
现在是一个好时机去了解在实践中成为torch.utils.data.Dataset子类意味着什么。看一下图 7.2,我们就能明白 PyTorch 的Dataset是什么。它是一个需要实现两个方法的对象:__len__和__getitem__。前者应该返回数据集中的项目数;后者应该返回项目,包括一个样本及其对应的标签(一个整数索引)。
在实践中,当一个 Python 对象配备了__len__方法时,我们可以将其作为参数传递给lenPython 内置函数:
# In[5]:
len(cifar10)
# Out[5]:
50000

图 7.2 PyTorch Dataset 对象的概念:它不一定保存数据,但通过 __len__ 和 __getitem__ 提供统一访问。
同样,由于数据集配备了 __getitem__ 方法,我们可以使用标准的下标索引元组和列表来访问单个项目。在这里,我们得到了一个 PIL(Python Imaging Library,PIL 包)图像,输出我们期望的整数值 1,对应于“汽车”:
# In[6]:
img, label = cifar10[99]
img, label, class_names[label]
# Out[6]:
(<PIL.Image.Image image mode=RGB size=32x32 at 0x7FB383657390>,
1,
'automobile')
因此,data.CIFAR10 数据集中的样本是 RGB PIL 图像的一个实例。我们可以立即绘制它:
# In[7]:
plt.imshow(img)
plt.show()
这产生了图 7.3 中显示的输出。这是一辆红色的汽车!³

图 7.3 CIFAR-10 数据集中的第 99 张图像:一辆汽车
7.1.3 数据集转换
这一切都很好,但我们可能需要一种方法在对其进行任何操作之前将 PIL 图像转换为 PyTorch 张量。这就是 torchvision.transforms 的作用。该模块定义了一组可组合的、类似函数的对象,可以作为参数传递给 torchvision 数据集,如 datasets.CIFAR10(...),并在加载数据后但在 __getitem__ 返回数据之前对数据执行转换。我们可以查看可用对象的列表如下:
# In[8]:
from torchvision import transforms
dir(transforms)
# Out[8]:
['CenterCrop',
'ColorJitter',
...
'Normalize',
'Pad',
'RandomAffine',
...
'RandomResizedCrop',
'RandomRotation',
'RandomSizedCrop',
...
'TenCrop',
'ToPILImage',
'ToTensor',
...
]
在这些转换中,我们可以看到 ToTensor,它将 NumPy 数组和 PIL 图像转换为张量。它还会确保输出张量的维度布局为 C × H × W(通道、高度、宽度;就像我们在第四章中介绍的那样)。
让我们尝试一下 ToTensor 转换。一旦实例化,它可以像一个函数一样调用,参数是 PIL 图像,返回一个张量作为输出:
# In[9]:
to_tensor = transforms.ToTensor()
img_t = to_tensor(img)
img_t.shape
# Out[9]:
torch.Size([3, 32, 32])
图像已经转换为 3 × 32 × 32 张量,因此是一个 3 通道(RGB)32 × 32 图像。请注意 label 没有发生任何变化;它仍然是一个整数。
正如我们预期的那样,我们可以直接将转换作为参数传递给 dataset .CIFAR10:
# In[10]:
tensor_cifar10 = datasets.CIFAR10(data_path, train=True, download=False,
transform=transforms.ToTensor())
此时,访问数据集的元素将返回一个张量,而不是一个 PIL 图像:
# In[11]:
img_t, _ = tensor_cifar10[99]
type(img_t)
# Out[11]:
torch.Tensor
如预期的那样,形状的第一个维度是通道,标量类型是 float32:
# In[12]:
img_t.shape, img_t.dtype
# Out[12]:
(torch.Size([3, 32, 32]), torch.float32)
原始 PIL 图像中的值范围从 0 到 255(每个通道 8 位),ToTensor 转换将数据转换为每个通道的 32 位浮点数,将值从 0.0 缩放到 1.0。让我们验证一下:
# In[13]:
img_t.min(), img_t.max()
# Out[13]:
(tensor(0.), tensor(1.))
现在让我们验证一下我们得到了相同的图像:
# In[14]:
plt.imshow(img_t.permute(1, 2, 0)) # ❶
plt.show()
# Out[14]:
<Figure size 432x288 with 1 Axes>
❶ 改变轴的顺序从 C × H × W 到 H × W × C
正如我们在图 7.4 中看到的,我们得到了与之前相同的输出。

图 7.4 我们已经见过这个。
检查通过。请注意,我们必须使用 permute 来改变轴的顺序,从 C × H × W 变为 H × W × C,以匹配 Matplotlib 的期望。
7.1.4 数据标准化
转换非常方便,因为我们可以使用 transforms.Compose 链接它们,它们可以透明地处理标准化和数据增强,直接在数据加载器中进行。例如,标准化数据集是一个好习惯,使得每个通道具有零均值和单位标准差。我们在第四章中提到过这一点,但现在,在经历了第五章之后,我们也对此有了直观的理解:通过选择在 0 加减 1(或 2)附近线性的激活函数,保持数据在相同范围内意味着神经元更有可能具有非零梯度,因此会更快地学习。此外,将每个通道标准化,使其具有相同的分布,将确保通道信息可以通过梯度下降混合和更新,使用相同的学习率。这就像在第 5.4.4 节中,当我们将权重重新缩放为与温度转换模型中的偏差相同数量级时的情况。
为了使每个通道的均值为零,标准差为单位,我们可以计算数据集中每个通道的均值和标准差,并应用以下转换:v_n[c] = (v[c] - mean[c]) / stdev[c]。这就是transforms.Normalize所做的。mean和stdev的值必须离线计算(它们不是由转换计算的)。让我们为 CIFAR-10 训练集计算它们。
由于 CIFAR-10 数据集很小,我们将能够完全在内存中操作它。让我们沿着额外的维度堆叠数据集返回的所有张量:
# In[15]:
imgs = torch.stack([img_t for img_t, _ in tensor_cifar10], dim=3)
imgs.shape
# Out[15]:
torch.Size([3, 32, 32, 50000])
现在我们可以轻松地计算每个通道的均值:
# In[16]:
imgs.view(3, -1).mean(dim=1) # ❶
# Out[16]:
tensor([0.4915, 0.4823, 0.4468])
❶ 请记住,view(3, -1)保留了三个通道,并将所有剩余的维度合并成一个,找出适当的大小。这里我们的 3 × 32 × 32 图像被转换成一个 3 × 1,024 向量,然后对每个通道的 1,024 个元素取平均值。
计算标准差类似:
# In[17]:
imgs.view(3, -1).std(dim=1)
# Out[17]:
tensor([0.2470, 0.2435, 0.2616])
有了这些数据,我们可以初始化Normalize转换
# In[18]:
transforms.Normalize((0.4915, 0.4823, 0.4468), (0.2470, 0.2435, 0.2616))
# Out[18]:
Normalize(mean=(0.4915, 0.4823, 0.4468), std=(0.247, 0.2435, 0.2616))
并在ToTensor转换后连接它:
# In[19]:
transformed_cifar10 = datasets.CIFAR10(
data_path, train=True, download=False,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4915, 0.4823, 0.4468),
(0.2470, 0.2435, 0.2616))
]))
请注意,在这一点上,绘制从数据集中绘制的图像不会为我们提供实际图像的忠实表示:
# In[21]:
img_t, _ = transformed_cifar10[99]
plt.imshow(img_t.permute(1, 2, 0))
plt.show()
我们得到的重新归一化的红色汽车如图 7.5 所示。这是因为归一化已经将 RGB 级别移出了 0.0 到 1.0 的范围,并改变了通道的整体幅度。所有的数据仍然存在;只是 Matplotlib 将其渲染为黑色。我们将记住这一点以备将来参考。

图 7.5 归一化后的随机 CIFAR-10 图像
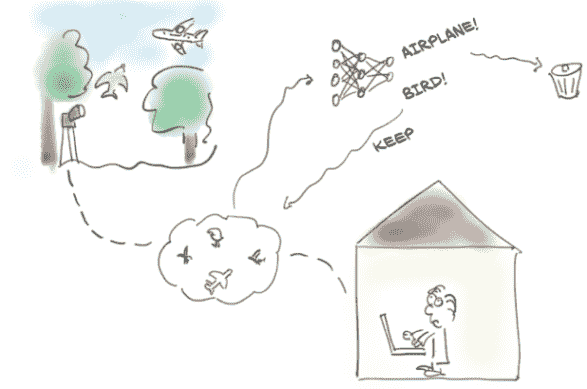
图 7.6 手头的问题:我们将帮助我们的朋友为她的博客区分鸟和飞机,通过训练一个神经网络来完成这项任务。
尽管如此,我们加载了一个包含成千上万张图片的花哨数据集!这非常方便,因为我们正需要这样的东西。
7.2 区分鸟和飞机
珍妮,我们在观鸟俱乐部的朋友,在机场南部的树林里设置了一组摄像头。当有东西进入画面时,摄像头应该保存一张照片并上传到俱乐部的实时观鸟博客。问题是,许多从机场进出的飞机最终触发了摄像头,所以珍妮花了很多时间从博客中删除飞机的照片。她需要的是一个像图 7.6 中所示的自动化系统。她需要一个神经网络--如果我们喜欢花哨的营销说辞,那就是人工智能--来立即丢弃飞机。
别担心!我们会处理好的,没问题--我们刚好有了完美的数据集(多么巧合啊,对吧?)。我们将从我们的 CIFAR-10 数据集中挑选出所有的鸟和飞机,并构建一个可以区分鸟和飞机的神经网络。
7.2.1 构建数据集
第一步是将数据整理成正确的形状。我们可以创建一个仅包含鸟和飞机的Dataset子类。然而,数据集很小,我们只需要在数据集上进行索引和len操作。它实际上不必是torch.utils.data.dataset.Dataset的子类!那么,为什么不简单地过滤cifar10中的数据并重新映射标签,使它们连续呢?下面是具体操作:
# In[5]:
label_map = {0: 0, 2: 1}
class_names = ['airplane', 'bird']
cifar2 = [(img, label_map[label])
for img, label in cifar10
if label in [0, 2]]
cifar2_val = [(img, label_map[label])
for img, label in cifar10_val
if label in [0, 2]]
cifar2对象满足Dataset的基本要求--也就是说,__len__和__getitem__已经定义--所以我们将使用它。然而,我们应该意识到,这是一个聪明的捷径,如果我们在使用中遇到限制,我们可能希望实现一个合适的Dataset。⁴
我们有了数据集!接下来,我们需要一个模型来处理我们的数据。
7.2.2 一个全连接的模型
我们在第五章学习了如何构建一个神经网络。我们知道它是一个特征的张量输入,一个特征的张量输出。毕竟,一幅图像只是以空间配置排列的一组数字。好吧,我们还不知道如何处理空间配置部分,但理论上,如果我们只是取图像像素并将它们展平成一个长的 1D 向量,我们可以将这些数字视为输入特征,对吧?这就是图 7.7 所说明的。

图 7.7 将我们的图像视为一维值向量并在其上训练一个全连接分类器
让我们试试看。每个样本有多少特征?嗯,32 × 32 × 3:也就是说,每个样本有 3072 个输入特征。从我们在第五章构建的模型开始,我们的新模型将是一个具有 3072 个输入特征和一些隐藏特征数量的nn.Linear,然后是一个激活函数,然后是另一个将网络缩减到适当的输出特征数量(对于这种用例为 2)的nn.Linear:
# In[6]:
import torch.nn as nn
n_out = 2
model = nn.Sequential(
nn.Linear(
3072, # ❶
512, # ❷
),
nn.Tanh(),
nn.Linear(
512, # ❷
n_out, # ❸
)
)
❶ 输入特征
❷ 隐藏层大小
❸ 输出类别
我们有点随意地选择了 512 个隐藏特征。神经网络至少需要一个隐藏层(激活层,所以两个模块),中间需要一个非线性激活函数,以便能够学习我们在第 6.3 节中讨论的任意函数--否则,它将只是一个线性模型。隐藏特征表示(学习的)输入之间通过权重矩阵编码的关系。因此,模型可能会学习“比较”向量元素 176 和 208,但它并不会事先关注它们,因为它在结构上不知道这些实际上是(第 5 行,第 16 像素)和
(第 6 行,第 16 像素),因此是相邻的。
所以我们有了一个模型。接下来我们将讨论我们模型的输出应该是什么。
7.2.3 分类器的输出
在第六章中,网络产生了预测的温度(具有定量意义的数字)作为输出。我们可以在这里做类似的事情:使我们的网络输出一个单一的标量值(所以n_out = 1),将标签转换为浮点数(飞机为 0.0,鸟为 1.0),并将其用作MSELoss的目标(批次中平方差的平均值)。这样做,我们将问题转化为一个回归问题。然而,更仔细地观察,我们现在处理的是一种性质有点不同的东西。
我们需要认识到输出是分类的:它要么是飞机,要么是鸟(或者如果我们有所有 10 个原始类别的话,还可能是其他东西)。正如我们在第四章中学到的,当我们必须表示一个分类变量时,我们应该切换到该变量的一种独热编码表示,比如对于飞机是[1, 0],对于鸟是[0, 1](顺序是任意的)。如果我们有 10 个类别,如完整的 CIFAR-10 数据集,这仍然有效;我们将只有一个长度为 10 的向量。
在理想情况下,网络将为飞机输出torch.tensor([1.0, 0.0]),为鸟输出torch.tensor([0.0, 1.0])。实际上,由于我们的分类器不会是完美的,我们可以期望网络输出介于两者之间的值。在这种情况下的关键认识是,我们可以将输出解释为概率:第一个条目是“飞机”的概率,第二个是“鸟”的概率。
将问题转化为概率的形式对我们网络的输出施加了一些额外的约束:
-
输出的每个元素必须在
[0.0, 1.0]范围内(一个结果的概率不能小于 0 或大于 1)。 -
输出的元素必须加起来等于 1.0(我们确定两个结果中的一个将会发生)。
这听起来像是在一个数字向量上以可微分的方式强制执行一个严格的约束。然而,有一个非常聪明的技巧正是做到了这一点,并且是可微分的:它被称为softmax。
7.2.4 将输出表示为概率
Softmax 是一个函数,它接受一个值向量并产生另一个相同维度的向量,其中值满足我们刚刚列出的表示概率的约束条件。Softmax 的表达式如图 7.8 所示。

图 7.8 手写 softmax
也就是说,我们取向量的元素,计算元素的指数,然后将每个元素除以指数的总和。在代码中,就像这样:
# In[7]:
def softmax(x):
return torch.exp(x) / torch.exp(x).sum()
让我们在一个输入向量上测试一下:
# In[8]:
x = torch.tensor([1.0, 2.0, 3.0])
softmax(x)
# Out[8]:
tensor([0.0900, 0.2447, 0.6652])
如预期的那样,它满足概率的约束条件:
# In[9]:
softmax(x).sum()
# Out[9]:
tensor(1.)
Softmax 是一个单调函数,即输入中的较低值将对应于输出中的较低值。然而,它不是尺度不变的,即值之间的比率不被保留。事实上,输入的第一个和第二个元素之间的比率为 0.5,而输出中相同元素之间的比率为 0.3678。这并不是一个真正的问题,因为学习过程将以适当的比率调整模型的参数。
nn模块将 softmax 作为一个模块提供。由于通常输入张量可能具有额外的批次第 0 维,或者具有编码概率的维度和其他维度,nn.Softmax要求我们指定应用 softmax 函数的维度:
# In[10]:
softmax = nn.Softmax(dim=1)
x = torch.tensor([[1.0, 2.0, 3.0],
[1.0, 2.0, 3.0]])
softmax(x)
# Out[10]:
tensor([[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652]])
在这种情况下,我们有两个输入向量在两行中(就像我们处理批次时一样),因此我们初始化nn.Softmax以沿着第 1 维操作。
太棒了!我们现在可以在模型末尾添加一个 softmax,这样我们的网络就能够生成概率:
# In[11]:
model = nn.Sequential(
nn.Linear(3072, 512),
nn.Tanh(),
nn.Linear(512, 2),
nn.Softmax(dim=1))
实际上,我们可以在甚至训练模型之前尝试运行模型。让我们试试,看看会得到什么。我们首先构建一个包含一张图片的批次,我们的鸟(图 7.9):
# In[12]:
img, _ = cifar2[0]
plt.imshow(img.permute(1, 2, 0))
plt.show()

图 7.9 CIFAR-10 数据集中的一只随机鸟(归一化后)
哦,你好。为了调用模型,我们需要使输入具有正确的维度。我们记得我们的模型期望输入中有 3,072 个特征,并且nn将数据组织成沿着第零维的批次。因此,我们需要将我们的 3 × 32 × 32 图像转换为 1D 张量,然后在第零位置添加一个额外的维度。我们在第三章学习了如何做到这一点:
# In[13]:
img_batch = img.view(-1).unsqueeze(0)
现在我们准备调用我们的模型:
# In[14]:
out = model(img_batch)
out
# Out[14]:
tensor([[0.4784, 0.5216]], grad_fn=<SoftmaxBackward>)
所以,我们得到了概率!好吧,我们知道我们不应该太兴奋:我们的线性层的权重和偏置根本没有经过训练。它们的元素由 PyTorch 在-1.0 和 1.0 之间随机初始化。有趣的是,我们还看到输出的grad_fn,这是反向计算图的顶点(一旦我们需要反向传播时将被使用)。
另外,虽然我们知道哪个输出概率应该是哪个(回想一下我们的class_names),但我们的网络并没有这方面的指示。第一个条目是“飞机”,第二个是“鸟”,还是反过来?在这一点上,网络甚至无法判断。正是损失函数在反向传播后将这两个数字关联起来。如果标签提供为“飞机”索引 0 和“鸟”索引 1,那么输出将被诱导采取这个顺序。因此,在训练后,我们将能够通过计算输出概率的argmax来获得标签:也就是说,我们获得最大概率的索引。方便的是,当提供一个维度时,torch.max会返回沿着该维度的最大元素以及该值出现的索引。在我们的情况下,我们需要沿着概率向量(而不是跨批次)取最大值,因此是第 1 维:
# In[15]:
_, index = torch.max(out, dim=1)
index
# Out[15]:
tensor([1])
它说这张图片是一只鸟。纯属运气。但我们通过让模型输出概率来适应手头的分类任务,现在我们已经运行了我们的模型对输入图像进行验证,确保我们的管道正常工作。是时候开始训练了。与前两章一样,我们在训练过程中需要最小化的损失。
7.2.5 用于分类的损失
我们刚提到损失是给概率赋予意义的。在第 5 和第六章中,我们使用均方误差(MSE)作为我们的损失。我们仍然可以使用 MSE,并使我们的输出概率收敛到[0.0, 1.0]和[1.0, 0.0]。然而,仔细想想,我们并不真正关心精确复制这些值。回顾我们用于提取预测类别索引的 argmax 操作,我们真正感兴趣的是第一个概率对于飞机而言比第二个更高,对于鸟而言则相反。换句话说,我们希望惩罚错误分类,而不是费力地惩罚一切看起来不完全像 0.0 或 1.0 的东西。
在这种情况下,我们需要最大化的是与正确类别相关联的概率,out[class_index],其中out是 softmax 的输出,class_index是一个包含 0 表示“飞机”和 1 表示“鸟”的向量,对于每个样本。这个数量--即与正确类别相关联的概率--被称为似然度(给定数据的模型参数的)。换句话说,我们希望一个损失函数在似然度低时非常高:低到其他选择具有更高的概率。相反,当似然度高于其他选择时,损失应该很低,我们并不真正固执于将概率提高到 1。
有一个表现出这种行为的损失函数,称为负对数似然(NLL)。它的表达式为NLL = - sum(log(out_i[c_i])),其中求和是针对N个样本,c_i是样本i的正确类别。让我们看一下图 7.10,它显示了 NLL 作为预测概率的函数。

图 7.10 预测概率的 NLL 损失函数
图表显示,当数据被分配低概率时,NLL 增长到无穷大,而当概率大于 0.5 时,它以相对缓慢的速度下降。记住,NLL 以概率作为输入;因此,随着可能性增加,其他概率必然会减少。
总结一下,我们的分类损失可以计算如下。对于批次中的每个样本:
-
运行正向传播,并从最后(线性)层获取输出值。
-
计算它们的 softmax,并获得概率。
-
获取与正确类别对应的预测概率(参数的似然度)。请注意,我们知道正确类别是什么,因为这是一个监督问题--这是我们的真实值。
-
计算其对数,加上一个负号,并将其添加到损失中。
那么,在 PyTorch 中我们如何做到这一点呢?PyTorch 有一个nn.NLLLoss类。然而(注意),与您可能期望的相反,它不接受概率,而是接受对数概率的张量作为输入。然后,它计算给定数据批次的我们模型的 NLL。这种输入约定背后有一个很好的原因:当概率接近零时,取对数是棘手的。解决方法是使用nn.LogSoftmax而不是nn.Softmax,后者会确保计算在数值上是稳定的。
现在我们可以修改我们的模型,使用nn.LogSoftmax作为输出模块:
model = nn.Sequential(
nn.Linear(3072, 512),
nn.Tanh(),
nn.Linear(512, 2),
nn.LogSoftmax(dim=1))
然后我们实例化我们的 NLL 损失:
loss = nn.NLLLoss()
损失将nn.LogSoftmax的输出作为批次的第一个参数,并将类别索引的张量(在我们的情况下是零和一)作为第二个参数。现在我们可以用我们的小鸟来测试它:
img, label = cifar2[0]
out = model(img.view(-1).unsqueeze(0))
loss(out, torch.tensor([label]))
tensor(0.6509, grad_fn=<NllLossBackward>)
结束我们对损失的研究,我们可以看看使用交叉熵损失如何改善均方误差。在图 7.11 中,我们看到当预测偏离目标时,交叉熵损失有一些斜率(在低损失角落,正确类别被分配了预测概率为 99.97%),而我们在开始时忽略的均方误差更早饱和,关键是对于非常错误的预测也是如此。其根本原因是均方误差的斜率太低,无法弥补错误预测的 softmax 函数的平坦性。这就是为什么概率的均方误差不适用于分类工作。

图 7.11 预测概率与目标概率向量之间的交叉熵(左)和均方误差(右)作为预测分数的函数--也就是在(对数)softmax 之前
7.2.6 训练分类器
好了!我们准备好重新引入我们在第五章写的训练循环,并看看它是如何训练的(过程如图 7.12 所示):
import torch
import torch.nn as nn
model = nn.Sequential(
nn.Linear(3072, 512),
nn.Tanh(),
nn.Linear(512, 2),
nn.LogSoftmax(dim=1))
learning_rate = 1e-2
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_fn = nn.NLLLoss()
n_epochs = 100
for epoch in range(n_epochs):
for img, label in cifar2:
out = model(img.view(-1).unsqueeze(0))
loss = loss_fn(out, torch.tensor([label]))
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("Epoch: %d, Loss: %f" % (epoch, float(loss))) # ❶
❶ 打印最后一张图像的损失。在下一章中,我们将改进我们的输出,以便给出整个时代的平均值。
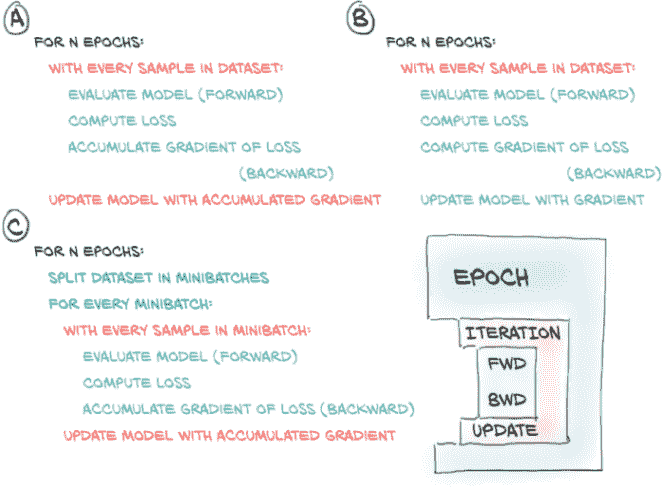
图 7.12 训练循环:(A)对整个数据集进行平均更新;(B)在每个样本上更新模型;(C)对小批量进行平均更新
更仔细地看,我们对训练循环进行了一点改变。在第五章,我们只有一个循环:在时代上(回想一下,一个时代在所有训练集中的样本都被评估完时结束)。我们认为在一个批次中评估所有 10,000 张图像会太多,所以我们决定有一个内部循环,在那里我们一次评估一个样本并在该单个样本上进行反向传播。
在第一种情况下,梯度在应用之前被累积在所有样本上,而在这种情况下,我们基于单个样本上梯度的非常部分估计来应用参数的变化。然而,基于一个样本减少损失的好方向可能不适用于其他样本。通过在每个时代对样本进行洗牌并在一次或(最好是为了稳定性)几个样本上估计梯度,我们有效地在梯度下降中引入了随机性。记得随机梯度下降(SGD)吗?这代表随机梯度下降,这就是S的含义:在洗牌数据的小批量(又称小批量)上工作。事实证明,遵循在小批量上估计的梯度,这些梯度是对整个数据集估计的梯度的较差近似,有助于收敛并防止优化过程在途中遇到的局部最小值中卡住。正如图 7.13 所示,来自小批量的梯度随机偏离理想轨迹,这也是为什么我们希望使用相当小的学习率的部分原因。在每个时代对数据集进行洗牌有助于确保在小批量上估计的梯度序列代表整个数据集上计算的梯度。
通常,小批量是一个在训练之前需要设置的固定大小,就像学习率一样。这些被称为超参数,以区别于模型的参数。
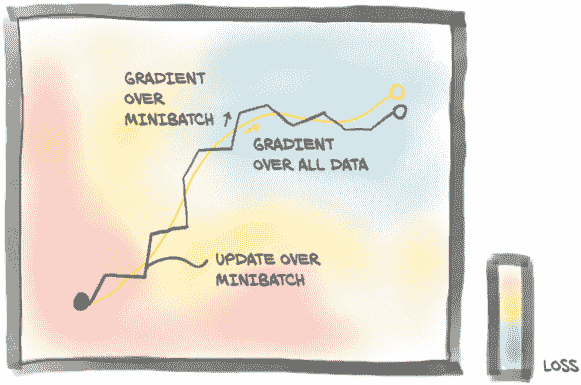
图 7.13 梯度下降在整个数据集上的平均值(浅色路径)与随机梯度下降,其中梯度是在随机选择的小批量上估计的。
在我们的训练代码中,我们选择了大小为 1 的小批量,一次从数据集中选择一个项目。torch.utils.data模块有一个帮助对数据进行洗牌和组织成小批量的类:DataLoader。数据加载器的工作是从数据集中抽样小批量,使我们能够选择不同的抽样策略。一个非常常见的策略是在每个时代洗牌数据后进行均匀抽样。图 7.14 显示了数据加载器对从Dataset获取的索引进行洗牌的过程。
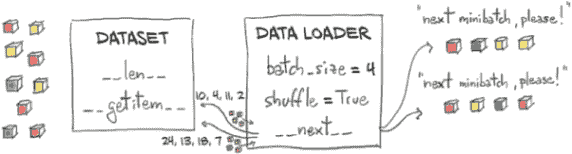
图 7.14 通过使用数据集来采样单个数据项来分发小批量数据的数据加载器
让我们看看这是如何完成的。至少,DataLoader构造函数需要一个Dataset对象作为输入,以及batch_size和一个布尔值shuffle,指示数据是否需要在每个 epoch 开始时进行洗牌:
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=True)
DataLoader可以被迭代,因此我们可以直接在新训练代码的内部循环中使用它:
import torch
import torch.nn as nn
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=True)
model = nn.Sequential(
nn.Linear(3072, 512),
nn.Tanh(),
nn.Linear(512, 2),
nn.LogSoftmax(dim=1))
learning_rate = 1e-2
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_fn = nn.NLLLoss()
n_epochs = 100
for epoch in range(n_epochs):
for imgs, labels in train_loader:
batch_size = imgs.shape[0]
outputs = model(imgs.view(batch_size, -1))
loss = loss_fn(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("Epoch: %d, Loss: %f" % (epoch, float(loss))) # ❶
❶ 由于洗牌,现在这会打印一个随机批次的损失--显然这是我们在第八章想要改进的地方
在每个内部迭代中,imgs是一个大小为 64 × 3 × 32 × 32 的张量--也就是说,64 个(32 × 32)RGB 图像的小批量--而labels是一个包含标签索引的大小为 64 的张量。
让我们运行我们的训练:
Epoch: 0, Loss: 0.523478
Epoch: 1, Loss: 0.391083
Epoch: 2, Loss: 0.407412
Epoch: 3, Loss: 0.364203
...
Epoch: 96, Loss: 0.019537
Epoch: 97, Loss: 0.008973
Epoch: 98, Loss: 0.002607
Epoch: 99, Loss: 0.026200
我们看到损失有所下降,但我们不知道是否足够低。由于我们的目标是正确地为图像分配类别,并最好在一个独立的数据集上完成,我们可以计算我们模型在验证集上的准确率,即正确分类的数量占总数的比例:
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size=64,
shuffle=False)
correct = 0
total = 0
with torch.no_grad():
for imgs, labels in val_loader:
batch_size = imgs.shape[0]
outputs = model(imgs.view(batch_size, -1))
_, predicted = torch.max(outputs, dim=1)
total += labels.shape[0]
correct += int((predicted == labels).sum())
print("Accuracy: %f", correct / total)
Accuracy: 0.794000
不是很好的性能,但比随机好得多。为我们辩护,我们的模型是一个相当浅的分类器;奇迹的是它居然工作了。这是因为我们的数据集非常简单--两类样本中很多样本可能有系统性差异(比如背景颜色),这有助于模型根据少量像素区分鸟类和飞机。
我们可以通过添加更多的层来为我们的模型增加一些亮点,这将增加模型的深度和容量。一个相当任意的可能性是
model = nn.Sequential(
nn.Linear(3072, 1024),
nn.Tanh(),
nn.Linear(1024, 512),
nn.Tanh(),
nn.Linear(512, 128),
nn.Tanh(),
nn.Linear(128, 2),
nn.LogSoftmax(dim=1))
在这里,我们试图将特征数量逐渐缓和到输出,希望中间层能更好地将信息压缩到越来越短的中间输出中。
nn.LogSoftmax和nn.NLLLoss的组合等效于使用nn.CrossEntropyLoss。这个术语是 PyTorch 的一个特殊之处,因为nn.NLLoss实际上计算交叉熵,但输入是对数概率预测,而nn.CrossEntropyLoss采用分数(有时称为对数几率)。从技术上讲,nn.NLLLoss是 Dirac 分布之间的交叉熵,将所有质量放在目标上,并且由对数概率输入给出的预测分布。
为了增加混乱,在信息理论中,这个交叉熵可以被解释为预测分布在目标分布下的负对数似然,经过样本大小归一化。因此,这两种损失都是模型参数的负对数似然,给定数据时,我们的模型预测(应用 softmax 后的)概率。在本书中,我们不会依赖这些细节,但当你在文献中看到这些术语时,不要让 PyTorch 的命名混淆你。
通常会从网络中删除最后一个nn.LogSoftmax层,并使用nn.CrossEntropyLoss作为损失函数。让我们试试:
model = nn.Sequential(
nn.Linear(3072, 1024),
nn.Tanh(),
nn.Linear(1024, 512),
nn.Tanh(),
nn.Linear(512, 128),
nn.Tanh(),
nn.Linear(128, 2))
loss_fn = nn.CrossEntropyLoss()
请注意,数字将与nn.LogSoftmax和nn.NLLLoss完全相同。只是一次性完成所有操作更方便,唯一需要注意的是,我们模型的输出将无法解释为概率(或对数概率)。我们需要明确通过 softmax 传递输出以获得这些概率。
训练这个模型并在验证集上评估准确率(0.802000)让我们意识到,一个更大的模型带来了准确率的提高,但并不多。训练集上的准确率几乎完美(0.998100)。这告诉我们什么?我们在两种情况下都过度拟合了我们的模型。我们的全连接模型通过记忆训练集来找到区分鸟类和飞机的方法,但在验证集上的表现并不是很好,即使我们选择了一个更大的模型。
PyTorch 通过nn.Model的parameters()方法(我们用来向优化器提供参数的相同方法)提供了一种快速确定模型有多少参数的方法。要找出每个张量实例中有多少元素,我们可以调用numel方法。将它们相加就得到了我们的总数。根据我们的用例,计算参数可能需要我们检查参数是否将requires_grad设置为True。我们可能希望区分可训练参数的数量与整个模型大小。让我们看看我们现在有什么:
# In[7]:
numel_list = [p.numel()
for p in connected_model.parameters()
if p.requires_grad == True]
sum(numel_list), numel_list
# Out[7]:
(3737474, [3145728, 1024, 524288, 512, 65536, 128, 256, 2])
哇,370 万个参数!对于这么小的输入图像来说,这不是一个小网络,是吗?即使我们的第一个网络也相当庞大:
# In[9]:
numel_list = [p.numel() for p in first_model.parameters()]
sum(numel_list), numel_list
# Out[9]:
(1574402, [1572864, 512, 1024, 2])
我们第一个模型中的参数数量大约是最新模型的一半。嗯,从单个参数大小的列表中,我们开始有了一个想法:第一个模块有 150 万个参数。在我们的完整网络中,我们有 1,024 个输出特征,这导致第一个线性模块有 3 百万个参数。这不应该出乎意料:我们知道线性层计算y = weight * x + bias,如果x的长度为 3,072(为简单起见忽略批处理维度),而y必须具有长度 1,024,则weight张量的大小需要为 1,024 × 3,072,bias大小必须为 1,024。而 1,024 * 3,072 + 1,024 = 3,146,752,正如我们之前发现的那样。我们可以直接验证这些数量:
# In[10]:
linear = nn.Linear(3072, 1024)
linear.weight.shape, linear.bias.shape
# Out[10]:
(torch.Size([1024, 3072]), torch.Size([1024]))
这告诉我们什么?我们的神经网络随着像素数量的增加不会很好地扩展。如果我们有一个 1,024 × 1,024 的 RGB 图像呢?那就是 3.1 百万个输入值。即使突然转向 1,024 个隐藏特征(这对我们的分类器不起作用),我们将有超过 30 亿个参数。使用 32 位浮点数,我们已经占用了 12 GB 的内存,甚至还没有到达第二层,更不用说计算和存储梯度了。这在大多数现代 GPU 上根本无法容纳。
7.2.7 完全连接的极限
让我们推理一下在图像的 1D 视图上使用线性模块意味着什么--图 7.15 展示了正在发生的事情。这就像是将每个输入值--也就是我们 RGB 图像中的每个分量--与每个输出特征的所有其他值进行线性组合。一方面,我们允许任何像素与图像中的每个其他像素进行组合,这可能与我们的任务相关。另一方面,我们没有利用相邻或远离像素的相对位置,因为我们将图像视为一个由数字组成的大向量。

图 7.15 使用带有输入图像的全连接模块:每个输入像素与其他每个像素组合以生成输出中的每个元素。
在一个 32 × 32 图像中捕捉到的飞机在蓝色背景上将非常粗略地类似于一个黑色的十字形状。如图 7.15 中的全连接网络需要学习,当像素 0,1 是黑色时,像素 1,1 也是黑色,依此类推,这是飞机的一个很好的指示。这在图 7.16 的上半部分有所说明。然而,将相同的飞机向下移动一个像素或更多像图的下半部分一样,像素之间的关系将不得不从头开始重新学习:这次,当像素 0,2 是黑色时,像素 1,2 是黑色,依此类推时,飞机很可能存在。更具体地说,全连接网络不是平移不变的。这意味着一个经过训练以识别从位置 4,4 开始的斯皮特火机的网络将无法识别完全相同的从位置 8,8 开始的斯皮特火机。然后,我们必须增广数据集--也就是在训练过程中对图像应用随机平移--以便网络有机会在整个图像中看到斯皮特火机,我们需要对数据集中的每个图像都这样做(值得一提的是,我们可以连接一个来自torchvision.transforms的转换来透明地执行此操作)。然而,这种数据增广策略是有代价的:隐藏特征的数量--也就是参数的数量--必须足够大,以存储关于所有这些平移副本的信息。
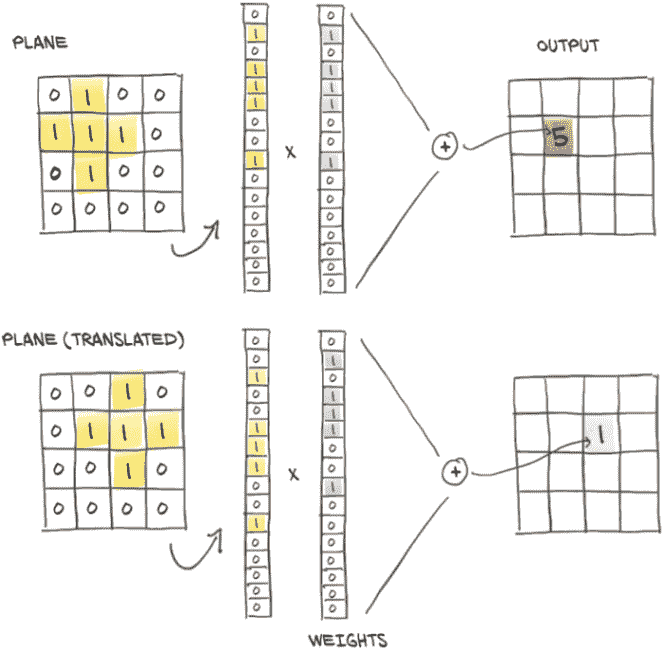
图 7.16 全连接层中的平移不变性或缺乏平移不变性
因此,在本章结束时,我们有了一个数据集,一个模型和一个训练循环,我们的模型学习了。然而,由于我们的问题与网络结构之间存在不匹配,我们最终过拟合了训练数据,而不是学习我们希望模型检测到的泛化特征。
我们已经创建了一个模型,允许将图像中的每个像素与其他像素相关联,而不考虑它们的空间排列。我们有一个合理的假设,即更接近的像素在理论上更相关。这意味着我们正在训练一个不具有平移不变性的分类器,因此如果我们希望在验证集上表现良好,我们被迫使用大量容量来学习平移副本。肯定有更好的方法,对吧?
当然,像这样的问题在这本书中大多是修辞性的。解决我们当前一系列问题的方法是改变我们的模型,使用卷积层。我们将在下一章中介绍这意味着什么。
7.3 结论
在本章中,我们解决了一个简单的分类问题,从数据集到模型,再到在训练循环中最小化适当的损失。所有这些都将成为你的 PyTorch 工具箱中的标准工具,并且使用它们所需的技能将在你使用 PyTorch 的整个期间都很有用。
我们还发现了我们模型的一个严重缺陷:我们一直将 2D 图像视为 1D 数据。此外,我们没有一种自然的方法来融入我们问题的平移不变性。在下一章中,您将学习如何利用图像数据的 2D 特性以获得更好的结果。⁹
我们可以立即利用所学知识处理没有这种平移不变性的数据。例如,在表格数据或我们在第四章中遇到的时间序列数据上使用它,我们可能已经可以做出很棒的事情。在一定程度上,也可以将其应用于适当表示的文本数据。¹⁰
7.4 练习
-
使用
torchvision实现数据的随机裁剪。-
结果图像与未裁剪的原始图像有何不同?
-
当第二次请求相同图像时会发生什么?
-
使用随机裁剪图像进行训练的结果是什么?
-
-
切换损失函数(也许是均方误差)。
-
训练行为是否会改变?
-
是否可能减少网络的容量,使其停止过拟合?
-
这样做时模型在验证集上的表现如何?
-
7.5 总结
-
计算机视觉是深度学习的最广泛应用之一。
-
有许多带有注释的图像数据集可以公开获取;其中许多可以通过
torchvision访问。 -
Dataset和DataLoader为加载和采样数据集提供了简单而有效的抽象。 -
对于分类任务,在网络输出上使用 softmax 函数会产生满足概率解释要求的值。在这种情况下,用 softmax 的输出作为非负对数似然函数的输入得到的损失函数是理想的分类损失函数。在 PyTorch 中,softmax 和这种损失的组合称为交叉熵。
-
没有什么能阻止我们将图像视为像素值向量,使用全连接网络处理它们,就像处理任何其他数值数据一样。然而,这样做会使利用数据中的空间关系变得更加困难。
-
可以使用
nn.Sequential创建简单模型。
¹ 这些图像是由加拿大高级研究所(CIFAR)的 Krizhevsky、Nair 和 Hinton 收集和标记的,并且来自麻省理工学院计算机科学与人工智能实验室(CSAIL)的更大的未标记 32×32 彩色图像集合:“8000 万小图像数据集”。
² 对于一些高级用途,PyTorch 还提供了IterableDataset。这可以用于数据集中随机访问数据代价过高或没有意义的情况:例如,因为数据是即时生成的。
³ 这在打印时无法很好地翻译;你必须相信我们的话,或者在电子书或 Jupyter Notebook 中查看。
⁴ 在这里,我们手动构建了新数据集,并且还想重新映射类别。在某些情况下,仅需要获取给定数据集的索引子集即可。这可以通过torch.utils.data.Subset类来实现。类似地,ConcatDataset用于将(兼容项的)数据集合并为一个更大的数据集。对于可迭代数据集,ChainDataset提供了一个更大的可迭代数据集。
⁵ 在“概率”向量上使用距离已经比使用MSELoss与类别编号要好得多——回想我们在第四章“连续、有序和分类值”侧边栏中讨论的值类型,对于类别来说,使用MSELoss没有意义,在实践中根本不起作用。然而,MSELoss并不适用于分类问题。
⁶ 对于特殊的二元分类情况,在这里使用两个值是多余的,因为一个总是另一个的 1 减。事实上,PyTorch 允许我们仅在模型末尾使用nn.Sigmoid激活输出单个概率,并使用二元交叉熵损失函数nn.BCELoss。还有一个将这两个步骤合并的nn.BCELossWithLogits。
⁷ 虽然原则上可以说这里的模型不确定(因为它将 48%和 52%的概率分配给两个类别),但典型的训练结果是高度自信的模型。贝叶斯神经网络可以提供一些补救措施,但这超出了本书的范围。
⁸ 要了解术语的简明定义,请参考 David MacKay 的《信息理论、推断和学习算法》(剑桥大学出版社,2003 年),第 2.3 节。
⁹ 关于平移不变性的同样警告也适用于纯粹的 1D 数据:音频分类器应该在要分类的声音开始时间提前或延后十分之一秒时产生相同的输出。
¹⁰词袋模型,只是对单词嵌入进行平均处理,可以使用本章的网络设计进行处理。更现代的模型考虑了单词的位置,并需要更高级的模型。
八、使用卷积进行泛化
本章涵盖
-
理解卷积
-
构建卷积神经网络
-
创建自定义
nn.Module子类 -
模块和功能 API 之间的区别
-
神经网络的设计选择
在上一章中,我们构建了一个简单的神经网络,可以拟合(或过拟合)数据,这要归功于线性层中可用于优化的许多参数。然而,我们的模型存在问题,它更擅长记忆训练集,而不是泛化鸟类和飞机的属性。根据我们的模型架构,我们猜测这是为什么。由于需要完全连接的设置来检测图像中鸟或飞机的各种可能的平移,我们有太多的参数(使模型更容易记忆训练集)和没有位置独立性(使泛化更困难)。正如我们在上一章中讨论的,我们可以通过使用各种重新裁剪的图像来增加我们的训练数据,以尝试强制泛化,但这不会解决参数过多的问题。
有一种更好的方法!它包括用不同的线性操作替换我们神经网络单元中的密集、全连接的仿射变换:卷积。
8.1 卷积的理由
让我们深入了解卷积是什么以及我们如何在神经网络中使用它们。是的,是的,我们正在努力区分鸟和飞机,我们的朋友仍在等待我们的解决方案,但这个偏离值得额外花费的时间。我们将对计算机视觉中这个基础概念发展直觉,然后带着超能力回到我们的问题。
在本节中,我们将看到卷积如何提供局部性和平移不变性。我们将通过仔细查看定义卷积的公式并使用纸和笔应用它来做到这一点——但不用担心,要点将在图片中,而不是公式中。
我们之前说过,将我们的输入图像以 1D 视图呈现,并将其乘以一个n_output_features × n_input_features的权重矩阵,就像在nn.Linear中所做的那样,意味着对于图像中的每个通道,计算所有像素的加权和,乘以一组权重,每个输出特征一个。
我们还说过,如果我们想要识别与对象对应的模式,比如天空中的飞机,我们可能需要查看附近像素的排列方式,而不太关心远离彼此的像素如何组合。基本上,我们的斯皮特火箭的图像是否在角落里有树、云或风筝并不重要。
为了将这种直觉转化为数学形式,我们可以计算像素与其相邻像素的加权和,而不是与图像中的所有其他像素。这相当于构建权重矩阵,每个输出特征和输出像素位置一个,其中距离中心像素一定距离的所有权重都为零。这仍然是一个加权和:即,一个线性操作。
8.1.1 卷积的作用
我们之前确定了另一个期望的属性:我们希望这些局部模式对输出产生影响,而不管它们在图像中的位置如何:也就是说,要平移不变。为了在应用于我们在第七章中使用的图像-作为-向量的矩阵中实现这一目标,需要实现一种相当复杂的权重模式(如果它太复杂,不用担心;很快就会好转):大多数权重矩阵将为零(对应于距离输出像素太远而不会产生影响的输入像素的条目)。对于其他权重,我们必须找到一种方法来保持与输入和输出像素相同相对位置对应的条目同步。这意味着我们需要将它们初始化为相同的值,并确保所有这些绑定权重在训练期间网络更新时保持不变。这样,我们可以确保权重在邻域内运作以响应局部模式,并且无论这些局部模式在图像中的位置如何,都能识别出来。
当然,这种方法远非实用。幸运的是,图像上有一个现成的、局部的、平移不变的线性操作:卷积。我们可以对卷积提出更简洁的描述,但我们将要描述的正是我们刚刚勾勒的内容——只是从不同角度来看。
卷积,或更准确地说,离散卷积¹(这里有一个我们不会深入讨论的连续版本),被定义为 2D 图像的权重矩阵,卷积核,与输入中的每个邻域的点积。考虑一个 3 × 3 的卷积核(在深度学习中,我们通常使用小卷积核;稍后我们会看到原因)作为一个 2D 张量
weight = torch.tensor([[w00, w01, w02],
[w10, w11, w12],
[w20, w21, w22]])
以及一个 1 通道的 MxN 图像:
image = torch.tensor([[i00, i01, i02, i03, ..., i0N],
[i10, i11, i12, i13, ..., i1N],
[i20, i21, i22, i23, ..., i2N],
[i30, i31, i32, i33, ..., i3N],
...
[iM0, iM1m iM2, iM3, ..., iMN]])
我们可以计算输出图像的一个元素(不包括偏置)如下:
o11 = i11 * w00 + i12 * w01 + i22 * w02 +
i21 * w10 + i22 * w11 + i23 * w12 +
i31 * w20 + i32 * w21 + i33 * w22
图 8.1 展示了这个计算的过程。
也就是说,我们在输入图像的i11位置上“平移”卷积核,并将每个权重乘以相应位置的输入图像的值。因此,输出图像是通过在所有输入位置上平移卷积核并执行加权求和来创建的。对于多通道图像,如我们的 RGB 图像,权重矩阵将是一个 3 × 3 × 3 矩阵:每个通道的一组权重共同贡献到输出值。
请注意,就像nn.Linear的weight矩阵中的元素一样,卷积核中的权重事先是未知的,但它们是随机初始化并通过反向传播进行更新的。还要注意,相同的卷积核,因此卷积核中的每个权重,在整个图像中都会被重复使用。回想自动求导,这意味着每个权重的使用都有一个跨越整个图像的历史。因此,损失相对于卷积权重的导数包含整个图像的贡献。
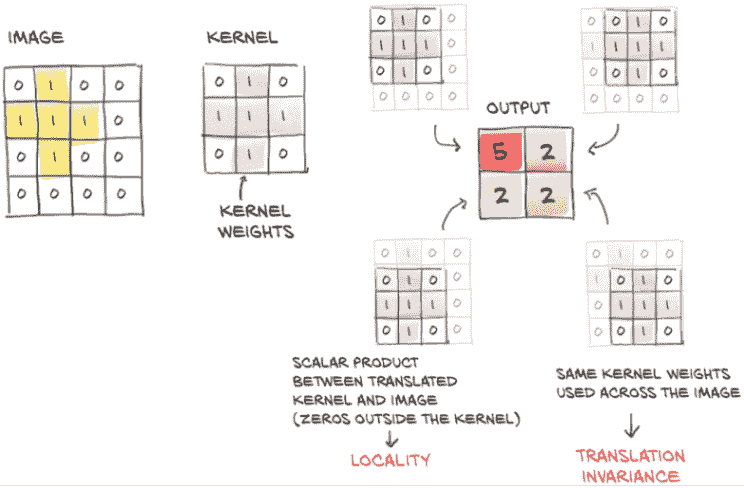
图 8.1 卷积:局部性和平移不变性
现在可以看到与之前所述的连接:卷积等同于具有多个线性操作,其权重几乎在每个像素周围为零,并且在训练期间接收相等的更新。
总结一下,通过转换为卷积,我们得到
-
对邻域进行局部操作
-
平移不变性
-
具有更少参数的模型
第三点的关键见解是,使用卷积层,参数的数量不取决于图像中的像素数量,就像在我们的全连接模型中一样,而是取决于卷积核的大小(3 × 3、5 × 5 等)以及我们决定在模型中使用多少卷积滤波器(或输出通道)。
8.2 卷积的实际应用
好吧,看起来我们已经花了足够的时间在一个兔子洞里!让我们看看 PyTorch 在我们的鸟类对比飞机挑战中的表现。torch.nn模块提供了 1、2 和 3 维的卷积:nn.Conv1d用于时间序列,nn.Conv2d用于图像,nn.Conv3d用于体积或视频。
对于我们的 CIFAR-10 数据,我们将使用nn.Conv2d。至少,我们提供给nn.Conv2d的参数是输入特征的数量(或通道,因为我们处理多通道图像:也就是,每个像素有多个值),输出特征的数量,以及内核的大小。例如,对于我们的第一个卷积模块,每个像素有 3 个输入特征(RGB 通道),输出中有任意数量的通道--比如,16。输出图像中的通道越多,网络的容量就越大。我们需要通道能够检测许多不同类型的特征。此外,因为我们是随机初始化它们的,所以即使在训练之后,我们得到的一些特征也会被证明是无用的。让我们坚持使用 3 × 3 的内核大小。
在所有方向上具有相同大小的内核尺寸是非常常见的,因此 PyTorch 为此提供了一个快捷方式:每当为 2D 卷积指定kernel_size=3时,它表示 3 × 3(在 Python 中提供为元组(3, 3))。对于 3D 卷积,它表示 3 × 3 × 3。我们将在本书第 2 部分中看到的 CT 扫描在三个轴中的一个轴上具有不同的体素(体积像素)分辨率。在这种情况下,考虑在特殊维度上具有不同大小的内核是有意义的。但现在,我们将坚持在所有维度上使用相同大小的卷积:
# In[11]:
conv = nn.Conv2d(3, 16, kernel_size=3) # ❶
conv
# Out[11]:
Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1))
❶ 与快捷方式kernel_size=3相比,我们可以等效地传递我们在输出中看到的元组:kernel_size=(3, 3)。
我们期望weight张量的形状是什么?卷积核的大小为 3 × 3,因此我们希望权重由 3 × 3 部分组成。对于单个输出像素值,我们的卷积核会考虑,比如,in_ch = 3 个输入通道,因此单个输出像素值的权重分量(以及整个输出通道的不变性)的形状为in_ch × 3 × 3。最后,我们有与输出通道一样多的权重组件,这里out_ch = 16,因此完整的权重张量是out_ch × in_ch × 3 × 3,在我们的情况下是 16 × 3 × 3 × 3。偏置的大小将为 16(为了简单起见,我们已经有一段时间没有讨论偏置了,但就像在线性模块的情况下一样,它是一个我们添加到输出图像的每个通道的常数值)。让我们验证我们的假设:
# In[12]:
conv.weight.shape, conv.bias.shape
# Out[12]:
(torch.Size([16, 3, 3, 3]), torch.Size([16]))
我们可以看到卷积是从图像中学习的方便选择。我们有更小的模型寻找局部模式,其权重在整个图像上进行优化。
2D 卷积通过产生一个 2D 图像作为输出,其像素是输入图像邻域的加权和。在我们的情况下,卷积核权重和偏置conv.weight都是随机初始化的,因此输出图像不会特别有意义。通常情况下,如果我们想要使用一个输入图像调用conv模块,我们需要使用unsqueeze添加零批次维度,因为nn.Conv2d期望输入为B × C × H × W形状的张量:
# In[13]:
img, _ = cifar2[0]
output = conv(img.unsqueeze(0))
img.unsqueeze(0).shape, output.shape
# Out[13]:
(torch.Size([1, 3, 32, 32]), torch.Size([1, 16, 30, 30]))
我们很好奇,所以我们可以显示输出,如图 8.2 所示:
# In[15]:
plt.imshow(output[0, 0].detach(), cmap='gray')
plt.show()

图 8.2 我们的鸟经过随机卷积处理后的样子。(我们在代码中作弊一点,以展示给您输入。)
等一下。让我们看看output的大小:它是torch.Size([1, 16, 30, 30])。嗯;我们在过程中丢失了一些像素。这是怎么发生的?
8.2.1 填充边界
我们的输出图像比输入图像小的事实是决定在图像边界做什么的副作用。将卷积核应用为 3×3 邻域像素的加权和要求在所有方向上都有邻居。如果我们在 i00 处,我们只有右侧和下方的像素。默认情况下,PyTorch 将在输入图片内滑动卷积核,获得width - kernel_width + 1 个水平和垂直位置。对于奇数大小的卷积核,这导致图像在每一侧缩小卷积核宽度的一半(在我们的情况下,3//2 = 1)。这解释了为什么每个维度都缺少两个像素。

图 8.3 零填充以保持输出中的图像大小
然而,PyTorch 给了我们填充图像的可能性,通过在边界周围创建幽灵像素,这些像素在卷积方面的值为零。图 8.3 展示了填充的效果。
在我们的情况下,当kernel_size=3时指定padding=1意味着 i00 上方和左侧有额外的邻居,这样原始图像的角落处甚至可以计算卷积的输出。³最终结果是输出现在与输入具有完全相同的大小:
# In[16]:
conv = nn.Conv2d(3, 1, kernel_size=3, padding=1) # ❶
output = conv(img.unsqueeze(0))
img.unsqueeze(0).shape, output.shape
# Out[16]:
(torch.Size([1, 3, 32, 32]), torch.Size([1, 1, 32, 32]))
❶ 现在有填充了
请注意,无论是否使用填充,weight和bias的大小都不会改变。
填充卷积有两个主要原因。首先,这样做有助于我们分离卷积和改变图像大小的问题,这样我们就少了一件事要记住。其次,当我们有更复杂的结构,比如跳跃连接(在第 8.5.3 节讨论)或我们将在第 2 部分介绍的 U-Net 时,我们希望几个卷积之前和之后的张量具有兼容的大小,以便我们可以将它们相加或取差异。
8.2.2 用卷积检测特征
我们之前说过,weight和bias是通过反向传播学习的参数,就像nn.Linear中的weight和bias一样。然而,我们可以通过手动设置权重来玩转卷积,看看会发生什么。
首先让我们将bias归零,以消除任何混淆因素,然后将weights设置为一个恒定值,以便输出中的每个像素得到其邻居的平均值。对于每个 3×3 邻域:
# In[17]:
with torch.no_grad():
conv.bias.zero_()
with torch.no_grad():
conv.weight.fill_(1.0 / 9.0)
我们本可以选择conv.weight.one_()--这将导致输出中的每个像素是邻域像素的总和。除了输出图像中的值会大九倍之外,没有太大的区别。
无论如何,让我们看看对我们的 CIFAR 图像的影响:
# In[18]:
output = conv(img.unsqueeze(0))
plt.imshow(output[0, 0].detach(), cmap='gray')
plt.show()
正如我们之前所预测的,滤波器产生了图像的模糊版本,如图 8.4 所示。毕竟,输出的每个像素都是输入邻域的平均值,因此输出中的像素是相关的,并且变化更加平滑。

图 8.4 我们的鸟,这次因为一个恒定的卷积核而变模糊
接下来,让我们尝试一些不同的东西。下面的卷积核一开始可能看起来有点神秘:
# In[19]:
conv = nn.Conv2d(3, 1, kernel_size=3, padding=1)
with torch.no_grad():
conv.weight[:] = torch.tensor([[-1.0, 0.0, 1.0],
[-1.0, 0.0, 1.0],
[-1.0, 0.0, 1.0]])
conv.bias.zero_()
对于位置在 2,2 的任意像素计算加权和,就像我们之前为通用卷积核所做的那样,我们得到
o22 = i13 - i11 +
i23 - i21 +
i33 - i31
它执行 i22 右侧所有像素与 i22 左侧像素的差值。如果卷积核应用于不同强度相邻区域之间的垂直边界,o22 将具有较高的值。如果卷积核应用于均匀强度区域,o22 将为零。这是一个边缘检测卷积核:卷积核突出显示了水平相邻区域之间的垂直边缘。

图 8.5 我们鸟身上的垂直边缘,感谢手工制作的卷积核
将卷积核应用于我们的图像,我们看到了图 8.5 中显示的结果。如预期,卷积核增强了垂直边缘。我们可以构建更多复杂的滤波器,例如用于检测水平或对角边缘,或十字形或棋盘格模式,其中“检测”意味着输出具有很高的幅度。事实上,计算机视觉专家的工作历来是提出最有效的滤波器组合,以便在图像中突出显示某些特征并识别对象。
在深度学习中,我们让核根据数据以最有效的方式进行估计:例如,以最小化我们在第 7.2.5 节中介绍的输出和地面真相之间的负交叉熵损失为目标。从这个角度来看,卷积神经网络的工作是估计一组滤波器组的核,这些核将在连续层中将多通道图像转换为另一个多通道图像,其中不同通道对应不同特征(例如一个通道用于平均值,另一个通道用于垂直边缘等)。图 8.6 显示了训练如何自动学习核。
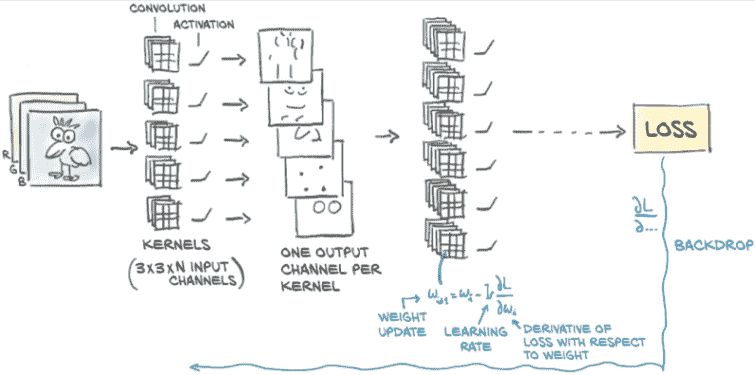
图 8.6 通过估计核权重的梯度并逐个更新它们以优化损失的卷积学习过程
8.2.3 深入探讨深度和池化
这一切都很好,但在概念上存在一个问题。我们之所以如此兴奋,是因为从全连接层转向卷积,我们实现了局部性和平移不变性。然后我们建议使用小卷积核,如 3 x 3 或 5 x 5:这确实是局部性的极致。那么大局观呢?我们怎么知道我们图像中的所有结构都是 3 像素或 5 像素宽的?好吧,我们不知道,因为它们不是。如果它们不是,我们的网络如何能够看到具有更大范围的这些模式?如果我们想有效解决鸟类与飞机的问题,我们真的需要这个,因为尽管 CIFAR-10 图像很小,但对象仍然具有跨越几个像素的(翼)跨度。
一种可能性是使用大型卷积核。当然,在极限情况下,我们可以为 32 x 32 图像使用 32 x 32 卷积核,但我们将收敛到旧的全连接、仿射变换,并丢失卷积的所有优点。另一种选项是在卷积神经网络中使用一层接一层的卷积,并在连续卷积之间同时对图像进行下采样。
从大到小:下采样
下采样原则上可以以不同方式发生。将图像缩小一半相当于将四个相邻像素作为输入,并产生一个像素作为输出。如何根据输入值计算输出值取决于我们。我们可以
-
对四个像素求平均值。这种平均池化曾经是一种常见方法,但现在已经不太受青睐。
-
取四个像素中的最大值。这种方法称为最大池化,目前是最常用的方法,但它的缺点是丢弃了其他四分之三的数据。
-
执行步幅卷积,只计算每第N个像素。具有步幅 2 的 3 x 4 卷积仍然包含来自前一层的所有像素的输入。文献显示了这种方法的前景,但它尚未取代最大池化。
我们将继续关注最大池化,在图 8.7 中有所说明。该图显示了最常见的设置,即取非重叠的 2 x 2 瓦片,并将每个瓦片中的最大值作为缩小比例后的新像素。
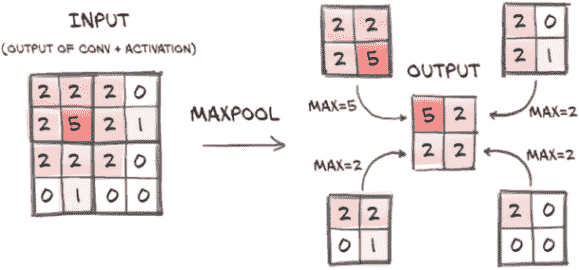
图 8.7 详细介绍了最大池化
直觉上,卷积层的输出图像,特别是因为它们后面跟着一个激活函数,往往在检测到对应于估计内核的某些特征(如垂直线)时具有较高的幅度。通过将 2×2 邻域中的最高值作为下采样输出,我们确保找到的特征幸存下采样,以弱响应为代价。
最大池化由nn.MaxPool2d模块提供(与卷积一样,也有适用于 1D 和 3D 数据的版本)。它的输入是要进行池化操作的邻域大小。如果我们希望将图像下采样一半,我们将使用大小为 2。让我们直接在输入图像上验证它是否按预期工作:
# In[21]:
pool = nn.MaxPool2d(2)
output = pool(img.unsqueeze(0))
img.unsqueeze(0).shape, output.shape
# Out[21]:
(torch.Size([1, 3, 32, 32]), torch.Size([1, 3, 16, 16]))
结合卷积和下采样以获得更好的效果
现在让我们看看如何结合卷积和下采样可以帮助我们识别更大的结构。在图 8.8 中,我们首先在我们的 8×8 图像上应用一组 3×3 内核,获得相同大小的多通道输出图像。然后我们将输出图像缩小一半,得到一个 4×4 图像,并对其应用另一组 3×3 内核。这第二组内核在已经缩小一半的东西的 3×3 邻域上有效地映射回输入的 8×8 邻域。此外,第二组内核获取第一组内核的输出(如平均值、边缘等特征)并在其上提取额外的特征。

图 8.8 通过手动进行更多卷积,展示叠加卷积和最大池化的效果:使用两个小的十字形内核和最大池化突出显示一个大的十字形。
因此,一方面,第一组内核在第一阶低级特征的小邻域上操作,而第二组内核有效地在更宽的邻域上操作,产生由前一特征组成的特征。这是一个非常强大的机制,使卷积神经网络能够看到非常复杂的场景--比我们的 CIFAR-10 数据集中的 32×32 图像复杂得多。
输出像素的感受野
当第二个 3×3 卷积内核在图 8.8 中的卷积输出中产生 21 时,这是基于第一个最大池输出的左上角 3×3 像素。它们又对应于第一个卷积输出左上角的 6×6 像素,而这又是由第一个卷积从左上角的 7×7 像素计算得出的。因此,第二个卷积输出中的像素受到 7×7 输入方块的影响。第一个卷积还使用隐式“填充”列和行来在角落产生输出;否则,我们将有一个 8×8 的输入像素方块通知第二个卷积输出中的给定像素(远离边界)。在花哨的语言中,我们说,3×3 卷积,2×2 最大池,3×3 卷积结构的给定输出神经元具有 8×8 的感受野。
8.2.4 将所有内容整合到我们的网络中
有了这些基本模块,我们现在可以继续构建用于检测鸟类和飞机的卷积神经网络。让我们以前的全连接模型作为起点,并像之前描述的那样引入nn.Conv2d和nn.MaxPool2d:
# In[22]:
model = nn.Sequential(
nn.Conv2d(3, 16, kernel_size=3, padding=1),
nn.Tanh(),
nn.MaxPool2d(2),
nn.Conv2d(16, 8, kernel_size=3, padding=1),
nn.Tanh(),
nn.MaxPool2d(2),
# ...
)
第一个卷积将我们从 3 个 RGB 通道转换为 16 个通道,从而使网络有机会生成 16 个独立特征,这些特征操作(希望)能够区分鸟和飞机的低级特征。然后我们应用Tanh激活函数。得到的 16 通道 32 × 32 图像通过第一个MaxPool3d池化为一个 16 通道 16 × 16 图像。此时,经过下采样的图像经历另一个卷积,生成一个 8 通道 16 × 16 输出。幸运的话,这个输出将由更高级的特征组成。再次,我们应用Tanh激活,然后池化为一个 8 通道 8 × 8 输出。
这会在哪里结束?在输入图像被减少为一组 8 × 8 特征之后,我们期望能够从网络中输出一些概率,然后将其馈送到我们的负对数似然函数中。然而,概率是一个一维向量中的一对数字(一个用于飞机,一个用于鸟),但在这里我们仍然处理多通道的二维特征。
回想一下本章的开头,我们已经知道我们需要做什么:将一个 8 通道 8 × 8 图像转换为一维向量,并用一组全连接层完成我们的网络:
# In[23]:
model = nn.Sequential(
nn.Conv2d(3, 16, kernel_size=3, padding=1),
nn.Tanh(),
nn.MaxPool2d(2),
nn.Conv2d(16, 8, kernel_size=3, padding=1),
nn.Tanh(),
nn.MaxPool2d(2),
# ... # ❶
nn.Linear(8 * 8 * 8, 32),
nn.Tanh(),
nn.Linear(32, 2))
❶ 警告:这里缺少重要内容!
这段代码给出了图 8.9 中显示的神经网络。

图 8.9 典型卷积网络的形状,包括我们正在构建的网络。图像被馈送到一系列卷积和最大池化模块,然后被拉直成一个一维向量,然后被馈送到全连接模块。
先忽略“缺少内容”的评论一分钟。让我们首先注意到线性层的大小取决于MaxPool2d的预期输出大小:8 × 8 × 8 = 512。让我们计算一下这个小模型的参数数量:
# In[24]:
numel_list = [p.numel() for p in model.parameters()]
sum(numel_list), numel_list
# Out[24]:
(18090, [432, 16, 1152, 8, 16384, 32, 64, 2])
对于这样小图像的有限数据集来说,这是非常合理的。为了增加模型的容量,我们可以增加卷积层的输出通道数(即每个卷积层生成的特征数),这将导致线性层的大小也增加。
我们在代码中放置“警告”注释是有原因的。模型没有运行的可能性:
# In[25]:
model(img.unsqueeze(0))
# Out[25]:
...
RuntimeError: size mismatch, m1: [64 x 8], m2: [512 x 32] at c:\...\THTensorMath.cpp:940
诚然,错误消息有点晦涩,但并不是太过复杂。我们在回溯中找到了linear的引用:回顾模型,我们发现只有一个模块必须有一个 512 × 32 的张量,即nn.Linear(512, 32),也就是最后一个卷积块后的第一个线性模块。
缺失的是将一个 8 通道 8 × 8 图像重塑为一个 512 元素的一维向量(如果忽略批处理维度,则为一维)。这可以通过在最后一个nn.MaxPool2d的输出上调用view来实现,但不幸的是,当我们使用nn.Sequential时,我们没有任何明确的方式查看每个模块的输出。
8.3 继承 nn.Module
在开发神经网络的某个阶段,我们会发现自己想要计算一些预制模块不涵盖的内容。在这里,这是一些非常简单的操作,比如重塑;但在第 8.5.3 节中,我们使用相同的构造来实现残差连接。因此,在本节中,我们学习如何制作自己的nn.Module子类,然后我们可以像预构建的模块或nn.Sequential一样使用它们。
当我们想要构建比仅仅一层接一层应用更复杂功能的模型时,我们需要离开nn.Sequential,转而使用能够为我们提供更大灵活性的东西。PyTorch 允许我们通过继承nn.Module来在模型中使用任何计算。
要对 nn.Module 进行子类化,至少需要定义一个接受模块输入并返回输出的 forward 函数。这是我们定义模块计算的地方。这里的 forward 名称让人想起了很久以前的一个时期,当模块需要定义我们在第 5.5.1 节中遇到的前向和后向传递时。使用标准的 torch 操作,PyTorch 将自动处理后向传递;实际上,nn.Module 从不带有 backward。
通常,我们的计算将使用其他模块--预制的如卷积或自定义的。要包含这些子模块,我们通常在构造函数 __init__ 中定义它们,并将它们分配给 self 以在 forward 函数中使用。它们将同时在我们模块的整个生命周期中保持其参数。请注意,您需要在执行这些操作之前调用 super().__init__()(否则 PyTorch 会提醒您)。
8.3.1 我们的网络作为 nn.Module
让我们将我们的网络编写为一个子模块。为此,我们在构造函数中实例化了所有之前传递给 nn.Sequential 的 nn.Conv2d、nn.Linear 等,然后在 forward 中依次使用它们的实例:
# In[26]:
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
self.act1 = nn.Tanh()
self.pool1 = nn.MaxPool2d(2)
self.conv2 = nn.Conv2d(16, 8, kernel_size=3, padding=1)
self.act2 = nn.Tanh()
self.pool2 = nn.MaxPool2d(2)
self.fc1 = nn.Linear(8 * 8 * 8, 32)
self.act3 = nn.Tanh()
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = self.pool1(self.act1(self.conv1(x)))
out = self.pool2(self.act2(self.conv2(out)))
out = out.view(-1, 8 * 8 * 8) # ❶
out = self.act3(self.fc1(out))
out = self.fc2(out)
return out
❶ 这种重塑是我们之前缺少的
Net 类在子模块方面等效于我们之前构建的 nn.Sequential 模型;但通过显式编写 forward 函数,我们可以直接操作 self.pool3 的输出并在其上调用 view 将其转换为 B × N 向量。请注意,在调用 view 时,我们将批处理维度保留为 -1,因为原则上我们不知道批处理中会有多少样本。
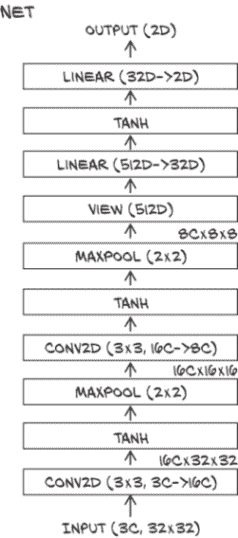
图 8.10 我们基准的卷积网络架构
在这里,我们使用 nn.Module 的子类来包含我们的整个模型。我们还可以使用子类来定义更复杂网络的新构建块。继续第六章中的图表风格,我们的网络看起来像图 8.10 所示的那样。我们正在对要在哪里呈现的信息做一些临时选择。
请记住,分类网络的目标通常是在某种意义上压缩信息,即我们从具有大量像素的图像开始,将其压缩为(概率向量的)类。关于我们的架构有两件事情值得与这个目标有关的评论。
首先,我们的目标反映在中间值的大小通常会缩小--这是通过在卷积中减少通道数、通过池化减少像素数以及在线性层中使输出维度低于输入维度来实现的。这是分类网络的一个共同特征。然而,在许多流行的架构中,如我们在第二章中看到的 ResNets 并在第 8.5.3 节中更多讨论的,通过在空间分辨率中进行池化来实现减少,但通道数增加(仍导致尺寸减小)。似乎我们的快速信息减少模式在深度有限且图像较小的网络中效果良好;但对于更深的网络,减少通常较慢。
其次,在一个层中,输出大小与输入大小没有减少:初始卷积。如果我们将单个输出像素视为一个具有 32 个元素的向量(通道),那么它是 27 个元素的线性变换(作为 3 个通道 × 3 × 3 核大小的卷积)--仅有轻微增加。在 ResNet 中,初始卷积从 147 个元素(3 个通道 × 7 × 7 核大小)生成 64 个通道。⁶ 因此,第一层在整体维度(如通道乘以像素)方面大幅增加数据流经过它,但对于独立考虑的每个输出像素,输出仍大致与输入相同。⁷
8.3.2 PyTorch 如何跟踪参数和子模块
有趣的是,在nn.Module中的属性中分配一个nn.Module实例,就像我们在早期的构造函数中所做的那样,会自动将模块注册为子模块。
注意 子模块必须是顶级属性,而不是嵌套在list或dict实例中!否则优化器将无法定位子模块(因此也无法定位它们的参数)。对于需要子模块列表或字典的模型情况,PyTorch 提供了nn.ModuleList和nn.ModuleDict。
我们可以调用nn.Module子类的任意方法。例如,对于一个模型,训练与预测等使用方式明显不同的情况下,可能有一个predict方法是有意义的。请注意,调用这些方法将类似于调用forward而不是模块本身--它们将忽略钩子,并且 JIT 在使用它们时不会看到模块结构,因为我们缺少第 6.2.1 节中显示的__call__位的等价物。
这使得Net可以访问其子模块的参数,而无需用户进一步操作:
# In[27]:
model = Net()
numel_list = [p.numel() for p in model.parameters()]
sum(numel_list), numel_list
# Out[27]:
(18090, [432, 16, 1152, 8, 16384, 32, 64, 2])
这里发生的情况是,parameters()调用深入到构造函数中分配为属性的所有子模块,并递归调用它们的parameters()。无论子模块嵌套多深,任何nn.Module都可以访问所有子参数的列表。通过访问它们的grad属性,该属性已被autograd填充,优化器将知道如何更改参数以最小化损失。我们从第五章中了解到这个故事。
现在我们知道如何实现我们自己的模块了--这在第 2 部分中我们将需要很多。回顾Net类的实现,并考虑在构造函数中注册子模块的实用性,以便我们可以访问它们的参数,看起来有点浪费,因为我们还注册了没有参数的子模块,如nn.Tanh和nn.MaxPool2d。直接在forward函数中调用这些是否更容易,就像我们调用view一样?
8.3.3 功能 API
当然会!这就是为什么 PyTorch 为每个nn模块都提供了functional对应项。这里所说的“functional”是指“没有内部状态”--换句话说,“其输出值完全由输入参数的值决定”。实际上,torch.nn.functional提供了许多像我们在nn中找到的模块一样工作的函数。但是,与模块对应项不同,它们不会像模块对应项那样在输入参数和存储参数上工作,而是将输入和参数作为函数调用的参数。例如,nn.Linear的功能对应项是nn.functional.linear,它是一个具有签名linear(input, weight, bias=None)的函数。weight和bias参数是函数调用的参数。
回到我们的模型,继续使用nn.Linear和nn.Conv2d的nn模块是有意义的,这样Net在训练期间将能够管理它们的Parameter。但是,我们可以安全地切换到池化和激活的功能对应项,因为它们没有参数:
# In[28]:
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(16, 8, kernel_size=3, padding=1)
self.fc1 = nn.Linear(8 * 8 * 8, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.tanh(self.conv1(x)), 2)
out = F.max_pool2d(torch.tanh(self.conv2(out)), 2)
out = out.view(-1, 8 * 8 * 8)
out = torch.tanh(self.fc1(out))
out = self.fc2(out)
return out
这比我们在第 8.3.1 节中之前定义的Net的定义要简洁得多,完全等效。请注意,在构造函数中实例化需要多个参数进行初始化的模块仍然是有意义的。
提示 虽然通用科学函数如tanh仍然存在于版本 1.0 的torch.nn.functional中,但这些入口点已被弃用,而是推荐使用顶级torch命名空间中的函数。像max_pool2d这样的更专业的函数将保留在torch.nn.functional中。
因此,功能方式也揭示了nn.Module API 的含义:Module是一个状态的容器,其中包含Parameter和子模块,以及执行前向操作的指令。
使用功能 API 还是模块化 API 是基于风格和品味的决定。当网络的一部分如此简单以至于我们想使用nn.Sequential时,我们处于模块化领域。当我们编写自己的前向传播时,对于不需要参数形式状态的事物,使用功能接口可能更自然。
在第十五章,我们将简要涉及量化。然后像激活这样的无状态位突然变得有状态,因为需要捕获有关量化的信息。这意味着如果我们打算量化我们的模型,如果我们选择非 JIT 量化,坚持使用模块化 API 可能是值得的。有一个风格问题将帮助您避免(最初未预料到的)用途带来的意外:如果您需要多个无状态模块的应用(如nn.HardTanh或nn.ReLU),最好为每个模块实例化一个单独的实例。重用相同的模块似乎很聪明,并且在这里使用标准 Python 时会给出正确的结果,但是分析您的模型的工具可能会出错。
现在我们可以自己制作nn.Module,并且在需要时还有功能 API 可用,当实例化然后调用nn.Module过于繁琐时。这是了解在 PyTorch 中实现的几乎任何神经网络的代码组织方式的最后一部分。
让我们再次检查我们的模型是否运行正常,然后我们将进入训练循环:
# In[29]:
model = Net()
model(img.unsqueeze(0))
# Out[29]:
tensor([[-0.0157, 0.1143]], grad_fn=<AddmmBackward>)
我们得到了两个数字!信息正确传递。我们现在可能意识不到,但在更复杂的模型中,正确设置第一个线性层的大小有时会导致挫折。我们听说过一些著名从业者输入任意数字,然后依靠 PyTorch 的错误消息来回溯线性层的正确大小。很烦人,对吧?不,这都是合法的!
8.4 训练我们的卷积网络
现在我们已经到了组装完整训练循环的时候。我们在第五章中已经开发了整体结构,训练循环看起来很像第六章的循环,但在这里我们将重新审视它以添加一些细节,如一些用于准确性跟踪的内容。在运行我们的模型之后,我们还会对更快速度有所期待,因此我们将学习如何在 GPU 上快速运行我们的模型。但首先让我们看看训练循环。
请记住,我们的卷积网络的核心是两个嵌套循环:一个是epochs上的外部循环,另一个是从我们的Dataset生成批次的DataLoader上的内部循环。在每个循环中,我们需要
-
通过模型传递输入(前向传播)。
-
计算损失(也是前向传播的一部分)。
-
将任何旧的梯度清零。
-
调用
loss.backward()来计算损失相对于所有参数的梯度(反向传播)。 -
使优化器朝着更低的损失方向迈出一步。
同时,我们收集并打印一些信息。所以这是我们的训练循环,看起来几乎与上一章相同--但记住每个事物的作用是很重要的:
# In[30]:
import datetime # ❶
def training_loop(n_epochs, optimizer, model, loss_fn, train_loader):
for epoch in range(1, n_epochs + 1): # ❷
loss_train = 0.0
for imgs, labels in train_loader: # ❸
outputs = model(imgs) # ❹
loss = loss_fn(outputs, labels) # ❺
optimizer.zero_grad() # ❻
loss.backward() # ❼
optimizer.step() # ❽
loss_train += loss.item() # ❾
if epoch == 1 or epoch % 10 == 0:
print('{} Epoch {}, Training loss {}'.format(
datetime.datetime.now(), epoch,
loss_train / len(train_loader))) # ❿
❶ 使用 Python 内置的 datetime 模块
❷ 我们在从 1 到 n_epochs 编号的 epochs 上循环,而不是从 0 开始
❸ 在数据加载器为我们创建的批次中循环遍历我们的数据集
❹ 通过我们的模型传递一个批次...
❺ ... 并计算我们希望最小化的损失
❻ 在摆脱上一轮梯度之后...
❼ ... 执行反向步骤。也就是说,我们计算我们希望网络学习的所有参数的梯度。
❽ 更新模型
❾ 对我们在 epoch 中看到的损失求和。请记住,将损失转换为 Python 数字并使用.item()是很重要的,以避免梯度。
❿ 除以训练数据加载器的长度以获得每批的平均损失。这比总和更直观。
我们使用第七章的Dataset;将其包装成DataLoader;像以前一样实例化我们的网络、优化器和损失函数;然后调用我们的训练循环。
与上一章相比,我们模型的重大变化是现在我们的模型是 nn.Module 的自定义子类,并且我们正在使用卷积。让我们在打印损失的同时运行 100 个周期的训练。根据您的硬件,这可能需要 20 分钟或更长时间才能完成!
# In[31]:
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=True) # ❶
model = Net() # # ❷
optimizer = optim.SGD(model.parameters(), lr=1e-2) # # ❸
loss_fn = nn.CrossEntropyLoss() # # ❹
training_loop( # ❺
n_epochs = 100,
optimizer = optimizer,
model = model,
loss_fn = loss_fn,
train_loader = train_loader,
)
# Out[31]:
2020-01-16 23:07:21.889707 Epoch 1, Training loss 0.5634813266954605
2020-01-16 23:07:37.560610 Epoch 10, Training loss 0.3277610331109375
2020-01-16 23:07:54.966180 Epoch 20, Training loss 0.3035225479086493
2020-01-16 23:08:12.361597 Epoch 30, Training loss 0.28249378549824855
2020-01-16 23:08:29.769820 Epoch 40, Training loss 0.2611226033253275
2020-01-16 23:08:47.185401 Epoch 50, Training loss 0.24105800626574048
2020-01-16 23:09:04.644522 Epoch 60, Training loss 0.21997178820477928
2020-01-16 23:09:22.079625 Epoch 70, Training loss 0.20370126601047578
2020-01-16 23:09:39.593780 Epoch 80, Training loss 0.18939699422401987
2020-01-16 23:09:57.111441 Epoch 90, Training loss 0.17283396527266046
2020-01-16 23:10:14.632351 Epoch 100, Training loss 0.1614033816868712
❶ DataLoader 对我们的 cifar2 数据集的示例进行批处理。Shuffling 使数据集中示例的顺序随机化。
❷ 实例化我们的网络 ...
❸ ... 我们一直在使用的随机梯度下降优化器 ...
❹ ... 以及我们在第 7.10 节中遇到的交叉熵损失
❺ 调用我们之前定义的训练循环
现在我们可以训练我们的网络了。但是,我们的鸟类观察者朋友在告诉她我们训练到非常低的训练损失时可能不会感到满意。
8.4.1 测量准确性
为了得到比损失更具可解释性的度量,我们可以查看训练和验证数据集上的准确率。我们使用了与第七章相同的代码:
# In[32]:
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=False)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size=64,
shuffle=False)
def validate(model, train_loader, val_loader):
for name, loader in [("train", train_loader), ("val", val_loader)]:
correct = 0
total = 0
with torch.no_grad(): # ❶
for imgs, labels in loader:
outputs = model(imgs)
_, predicted = torch.max(outputs, dim=1) # ❷
total += labels.shape[0] # ❸
correct += int((predicted == labels).sum()) # ❹
print("Accuracy {}: {:.2f}".format(name , correct / total))
validate(model, train_loader, val_loader)
# Out[32]:
Accuracy train: 0.93
Accuracy val: 0.89
❶ 我们这里不需要梯度,因为我们不想更新参数。
❷ 将最高值的索引作为输出给出
❸ 计算示例的数量,因此总数增加了批次大小
❹ 比较具有最大概率的预测类和地面真实标签,我们首先得到一个布尔数组。求和得到批次中预测和地面真实一致的项目数。
我们将转换为 Python 的 int--对于整数张量,这等同于使用 .item(),类似于我们在训练循环中所做的。
这比全连接模型要好得多,全连接模型只能达到 79%的准确率。我们在验证集上的错误数量几乎减半。而且,我们使用的参数要少得多。这告诉我们,模型在通过局部性和平移不变性从新样本中识别图像主题的任务中更好地泛化。现在我们可以让它运行更多周期,看看我们能够挤出什么性能。
8.4.2 保存和加载我们的模型
由于我们目前对我们的模型感到满意,所以实际上保存它会很好,对吧?这很容易做到。让我们将模型保存到一个文件中:
# In[33]:
torch.save(model.state_dict(), data_path + 'birds_vs_airplanes.pt')
birds_vs_airplanes.pt 文件现在包含了 model 的所有参数:即两个卷积模块和两个线性模块的权重和偏置。因此,没有结构--只有权重。这意味着当我们为我们的朋友在生产中部署模型时,我们需要保持 model 类方便,创建一个实例,然后将参数加载回去:
# In[34]:
loaded_model = Net() # ❶
loaded_model.load_state_dict(torch.load(data_path
+ 'birds_vs_airplanes.pt'))
# Out[34]:
<All keys matched successfully>
❶ 我们必须确保在保存和后续加载模型状态之间不更改 Net 的定义。
我们还在我们的代码库中包含了一个预训练模型,保存在 ../data/ p1ch7/birds_vs_airplanes.pt 中。
8.4.3 在 GPU 上训练
我们有一个网络并且可以训练它!但是让它变得更快会很好。到现在为止,我们通过将训练移至 GPU 来实现这一点并不奇怪。使用我们在第三章中看到的 .to 方法,我们可以将从数据加载器获取的张量移动到 GPU,之后我们的计算将自动在那里进行。但是我们还需要将参数移动到 GPU。令人高兴的是,nn.Module 实现了一个 .to 函数,将其所有参数移动到 GPU(或在传递 dtype 参数时转换类型)。
Module.to 和 Tensor.to 之间有一些微妙的区别。Module.to 是就地操作:模块实例被修改。但 Tensor.to 是非就地操作(在某种程度上是计算,就像 Tensor.tanh 一样),返回一个新的张量。一个影响是在将参数移动到适当设备后创建 Optimizer 是一个良好的实践。
如果有 GPU 可用,将事物移动到 GPU 被认为是一种良好的风格。一个好的模式是根据 torch.cuda.is_available 设置一个变量 device:
# In[35]:
device = (torch.device('cuda') if torch.cuda.is_available()
else torch.device('cpu'))
print(f"Training on device {device}.")
然后我们可以通过使用Tensor.to方法将从数据加载器获取的张量移动到 GPU 来修改训练循环。请注意,代码与本节开头的第一个版本完全相同,除了将输入移动到 GPU 的两行代码:
# In[36]:
import datetime
def training_loop(n_epochs, optimizer, model, loss_fn, train_loader):
for epoch in range(1, n_epochs + 1):
loss_train = 0.0
for imgs, labels in train_loader:
imgs = imgs.to(device=device) # ❶
labels = labels.to(device=device)
outputs = model(imgs)
loss = loss_fn(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train += loss.item()
if epoch == 1 or epoch % 10 == 0:
print('{} Epoch {}, Training loss {}'.format(
datetime.datetime.now(), epoch,
loss_train / len(train_loader)))
❶ 将图像和标签移动到我们正在训练的设备上的这两行是与我们之前版本的唯一区别。
对validate函数必须做出相同的修正。然后我们可以实例化我们的模型,将其移动到device,并像以前一样运行它:⁸
# In[37]:
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=True)
model = Net().to(device=device) # ❶
optimizer = optim.SGD(model.parameters(), lr=1e-2)
loss_fn = nn.CrossEntropyLoss()
training_loop(
n_epochs = 100,
optimizer = optimizer,
model = model,
loss_fn = loss_fn,
train_loader = train_loader,
)
# Out[37]:
2020-01-16 23:10:35.563216 Epoch 1, Training loss 0.5717791349265227
2020-01-16 23:10:39.730262 Epoch 10, Training loss 0.3285350770137872
2020-01-16 23:10:45.906321 Epoch 20, Training loss 0.29493294959994637
2020-01-16 23:10:52.086905 Epoch 30, Training loss 0.26962305994550134
2020-01-16 23:10:56.551582 Epoch 40, Training loss 0.24709946277794564
2020-01-16 23:11:00.991432 Epoch 50, Training loss 0.22623272664892446
2020-01-16 23:11:05.421524 Epoch 60, Training loss 0.20996672821462534
2020-01-16 23:11:09.951312 Epoch 70, Training loss 0.1934866009719053
2020-01-16 23:11:14.499484 Epoch 80, Training loss 0.1799132404908253
2020-01-16 23:11:19.047609 Epoch 90, Training loss 0.16620008706761774
2020-01-16 23:11:23.590435 Epoch 100, Training loss 0.15667157247662544
❶ 将我们的模型(所有参数)移动到 GPU。如果忘记将模型或输入移动到 GPU,将会出现关于张量不在同一设备上的错误,因为 PyTorch 运算符不支持混合 GPU 和 CPU 输入。
即使对于我们这里的小型网络,我们也看到了速度的显著增加。在大型模型上,使用 GPU 进行计算的优势更加明显。
在加载网络权重时存在一个小复杂性:PyTorch 将尝试将权重加载到与保存时相同的设备上--也就是说,GPU 上的权重将被恢复到 GPU 上。由于我们不知道是否要相同的设备,我们有两个选择:我们可以在保存之前将网络移动到 CPU,或者在恢复后将其移回。通过将map_location关键字参数传递给torch.load,更简洁地指示 PyTorch 在加载权重时覆盖设备信息:
# In[39]:
loaded_model = Net().to(device=device)
loaded_model.load_state_dict(torch.load(data_path
+ 'birds_vs_airplanes.pt',
map_location=device))
# Out[39]:
<All keys matched successfully>
8.5 模型设计
我们将我们的模型构建为nn.Module的子类,这是除了最简单的模型之外的事实标准。然后我们成功地训练了它,并看到了如何使用 GPU 来训练我们的模型。我们已经达到了可以构建一个前馈卷积神经网络并成功训练它来对图像进行分类的程度。自然的问题是,接下来呢?如果我们面对一个更加复杂的问题会怎么样?诚然,我们的鸟类与飞机数据集并不那么复杂:图像非常小,而且所研究的对象位于中心并占据了大部分视口。
如果我们转向,比如说,ImageNet,我们会发现更大、更复杂的图像,正确答案将取决于多个视觉线索,通常是按层次组织的。例如,当试图预测一个黑色砖块形状是遥控器还是手机时,网络可能正在寻找类似屏幕的东西。
此外,在现实世界中,图像可能不是我们唯一关注的焦点,我们还有表格数据、序列和文本。神经网络的承诺在于提供足够的灵活性,以解决所有这些类型数据的问题,只要有适当的架构(即层或模块的互连)和适当的损失函数。
PyTorch 提供了一个非常全面的模块和损失函数集合,用于实现从前馈组件到长短期记忆(LSTM)模块和变压器网络(这两种非常流行的顺序数据架构)的最新架构。通过 PyTorch Hub 或作为torchvision和其他垂直社区努力的一部分提供了几种模型。
我们将在第 2 部分看到一些更高级的架构,我们将通过分析 CT 扫描的端到端问题来介绍,但总的来说,探讨神经网络架构的变化超出了本书的范围。然而,我们可以借助迄今为止积累的知识来理解如何通过 PyTorch 的表现力实现几乎任何架构。本节的目的正是提供概念工具,使我们能够阅读最新的研究论文并开始在 PyTorch 中实现它--或者,由于作者经常发布他们论文的 PyTorch 实现,也可以在不被咖啡呛到的情况下阅读实现。
8.5.1 添加内存容量:宽度
鉴于我们的前馈架构,在进一步复杂化之前,我们可能想要探索一些维度。第一个维度是网络的宽度:每层的神经元数量,或者每个卷积的通道数。在 PyTorch 中,我们可以很容易地使模型更宽。我们只需在第一个卷积中指定更多的输出通道数,并相应增加后续层,同时要注意更改forward函数以反映这样一个事实,即一旦我们转换到全连接层,我们现在将有一个更长的向量:
# In[40]:
class NetWidth(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 32, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(32, 16, kernel_size=3, padding=1)
self.fc1 = nn.Linear(16 * 8 * 8, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.tanh(self.conv1(x)), 2)
out = F.max_pool2d(torch.tanh(self.conv2(out)), 2)
out = out.view(-1, 16 * 8 * 8)
out = torch.tanh(self.fc1(out))
out = self.fc2(out)
return out
如果我们想避免在模型定义中硬编码数字,我们可以很容易地将一个参数传递给init,并将宽度参数化,同时要注意在forward函数中也将view的调用参数化:
# In[42]:
class NetWidth(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.fc1 = nn.Linear(8 * 8 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.tanh(self.conv1(x)), 2)
out = F.max_pool2d(torch.tanh(self.conv2(out)), 2)
out = out.view(-1, 8 * 8 * self.n_chans1 // 2)
out = torch.tanh(self.fc1(out))
out = self.fc2(out)
return out
每一层指定通道和特征的数字与模型中的参数数量直接相关;其他条件相同的情况下,它们会增加模型的容量。就像之前所做的那样,我们可以看看我们的模型现在有多少参数:
# In[44]:
sum(p.numel() for p in model.parameters())
# Out[44]:
38386
容量越大,模型将能够处理输入的变化性就越多;但与此同时,过拟合的可能性也越大,因为模型可以使用更多的参数来记忆输入的不重要方面。我们已经探讨了对抗过拟合的方法,最好的方法是增加样本量,或者在没有新数据的情况下,通过对同一数据进行人工修改来增加现有数据。
在模型级别(而不是在数据上)我们可以采取一些更多的技巧来控制过拟合。让我们回顾一下最常见的几种。
8.5.2 帮助我们的模型收敛和泛化:正则化
训练模型涉及两个关键步骤:优化,当我们需要在训练集上减少损失时;和泛化,当模型不仅需要在训练集上工作,还需要在之前未见过的数据上工作,如验证集。旨在简化这两个步骤的数学工具有时被归纳为正则化的标签下。
控制参数:权重惩罚
稳定泛化的第一种方法是向损失中添加正则化项。这个项被设计成使模型的权重自行趋向于较小,限制训练使它们增长的程度。换句话说,这是对较大权重值的惩罚。这使得损失具有更加平滑的拓扑结构,从拟合单个样本中获得的收益相对较少。
这种类型的最受欢迎的正则化项是 L2 正则化,它是模型中所有权重的平方和,以及 L1 正则化,它是模型中所有权重的绝对值之和。它们都由一个(小)因子缩放,这是我们在训练之前设置的超参数。
L2 正则化也被称为权重衰减。这个名称的原因是,考虑到 SGD 和反向传播,L2 正则化项对参数w_i的负梯度为- 2 * lambda * w_i,其中lambda是前面提到的超参数,在 PyTorch 中简称为权重衰减。因此,将 L2 正则化添加到损失函数中等同于在优化步骤中减少每个权重的数量与其当前值成比例的量(因此,称为权重衰减)。请注意,权重衰减适用于网络的所有参数,如偏置。
在 PyTorch 中,我们可以通过向损失中添加一个项来很容易地实现正则化。在计算损失后,无论损失函数是什么,我们都可以迭代模型的参数,对它们各自的平方(对于 L2)或abs(对于 L1)求和,并进行反向传播:
# In[45]:
def training_loop_l2reg(n_epochs, optimizer, model, loss_fn,
train_loader):
for epoch in range(1, n_epochs + 1):
loss_train = 0.0
for imgs, labels in train_loader:
imgs = imgs.to(device=device)
labels = labels.to(device=device)
outputs = model(imgs)
loss = loss_fn(outputs, labels)
l2_lambda = 0.001
l2_norm = sum(p.pow(2.0).sum()
for p in model.parameters()) # ❶
loss = loss + l2_lambda * l2_norm
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train += loss.item()
if epoch == 1 or epoch % 10 == 0:
print('{} Epoch {}, Training loss {}'.format(
datetime.datetime.now(), epoch,
loss_train / len(train_loader)))
❶ 用 abs()替换 pow(2.0)以进行 L1 正则化
然而,PyTorch 中的 SGD 优化器已经有一个weight_decay参数,对应于2 * lambda,并且在更新过程中直接执行权重衰减,如前所述。这完全等同于将权重的 L2 范数添加到损失中,而无需在损失中累积项并涉及 autograd。
不要过分依赖单个输入:Dropout
一种有效的对抗过拟合策略最初是由 2014 年多伦多 Geoff Hinton 小组的 Nitish Srivastava 及其合著者提出的,题为“Dropout:一种简单防止神经网络过拟合的方法”(mng.bz/nPMa)。听起来就像是我们正在寻找的东西,对吧?dropout 背后的想法确实很简单:在整个网络中随机将一部分神经元的输出置零,其中随机化发生在每个训练迭代中。
该过程有效地在每次迭代中生成具有不同神经元拓扑的略有不同的模型,使模型中的神经元在发生过拟合时的记忆过程中有更少的协调机会。另一个观点是 dropout 扰乱了模型生成的特征,产生了一种接近增强的效果,但这次是在整个网络中。
在 PyTorch 中,我们可以通过在非线性激活函数和后续层的线性或卷积模块之间添加一个nn.Dropout模块来实现模型中的 dropout。作为参数,我们需要指定输入被置零的概率。在卷积的情况下,我们将使用专门的nn.Dropout2d或nn.Dropout3d,它们会将输入的整个通道置零:
# In[47]:
class NetDropout(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv1_dropout = nn.Dropout2d(p=0.4)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.conv2_dropout = nn.Dropout2d(p=0.4)
self.fc1 = nn.Linear(8 * 8 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.tanh(self.conv1(x)), 2)
out = self.conv1_dropout(out)
out = F.max_pool2d(torch.tanh(self.conv2(out)), 2)
out = self.conv2_dropout(out)
out = out.view(-1, 8 * 8 * self.n_chans1 // 2)
out = torch.tanh(self.fc1(out))
out = self.fc2(out)
return out
注意,在训练期间通常会激活 dropout,而在生产中评估经过训练的模型时,会绕过 dropout,或者等效地将概率分配为零。这通过Dropout模块的train属性来控制。请记住,PyTorch 允许我们通过调用在两种模式之间切换
model.train()
或
model.eval()
在任何nn.Model子类上。调用将自动复制到子模块,因此如果其中包含Dropout,它将在后续的前向和后向传递中相应地行为。
保持激活在适当范围内:批量归一化
在 2015 年,谷歌的 Sergey Ioffe 和 Christian Szegedy 发表了另一篇具有开创性意义的论文,名为“批量归一化:通过减少内部协变量转移加速深度网络训练”(arxiv.org/abs/1502.03167)。该论文描述了一种对训练有多种有益影响的技术:使我们能够增加学习率,使训练不那么依赖初始化并充当正则化器,从而代替了 dropout。
批量归一化背后的主要思想是重新缩放网络的激活输入,以便小批量具有某种理想的分布。回顾学习的机制和非线性激活函数的作用,这有助于避免输入到激活函数过于饱和部分,从而杀死梯度并减慢训练速度。
在实际操作中,批量归一化使用小批量样本中在该中间位置收集的均值和标准差来移位和缩放中间输入。正则化效果是因为模型始终将单个样本及其下游激活视为根据随机提取的小批量样本的统计数据而移位和缩放。这本身就是一种原则性的增强。论文的作者建议使用批量归一化消除或至少减轻了对 dropout 的需求。
在 PyTorch 中,批量归一化通过nn.BatchNorm1D、nn.BatchNorm2d和nn.BatchNorm3d模块提供,取决于输入的维度。由于批量归一化的目的是重新缩放激活的输入,自然的位置是在线性变换(在这种情况下是卷积)和激活之后,如下所示:
# In[49]:
class NetBatchNorm(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv1_batchnorm = nn.BatchNorm2d(num_features=n_chans1)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.conv2_batchnorm = nn.BatchNorm2d(num_features=n_chans1 // 2)
self.fc1 = nn.Linear(8 * 8 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = self.conv1_batchnorm(self.conv1(x))
out = F.max_pool2d(torch.tanh(out), 2)
out = self.conv2_batchnorm(self.conv2(out))
out = F.max_pool2d(torch.tanh(out), 2)
out = out.view(-1, 8 * 8 * self.n_chans1 // 2)
out = torch.tanh(self.fc1(out))
out = self.fc2(out)
return out
与 dropout 一样,批量归一化在训练和推断期间需要有不同的行为。实际上,在推断时,我们希望避免特定输入的输出依赖于我们向模型呈现的其他输入的统计信息。因此,我们需要一种方法来进行归一化,但这次是一次性固定归一化参数。
当处理小批量时,除了估计当前小批量的均值和标准差之外,PyTorch 还更新代表整个数据集的均值和标准差的运行估计,作为近似值。这样,当用户指定时
model.eval()
如果模型包含批量归一化模块,则冻结运行估计并用于归一化。要解冻运行估计并返回使用小批量统计信息,我们调用model.train(),就像我们对待 dropout 一样。
8.5.3 深入学习更复杂的结构:深度
早些时候,我们谈到宽度作为第一个要处理的维度,以使模型更大,从某种意义上说,更有能力。第二个基本维度显然是深度。由于这是一本深度学习书,深度是我们应该关注的东西。毕竟,深层模型总是比浅层模型更好,不是吗?嗯,这取决于情况。随着深度增加,网络能够逼近的函数的复杂性通常会增加。就计算机视觉而言,一个较浅的网络可以识别照片中的人的形状,而一个更深的网络可以识别人、头部上半部分的脸和脸部内的嘴巴。深度使模型能够处理分层信息,当我们需要理解上下文以便对某些输入进行分析时。
还有另一种思考深度的方式:增加深度与增加网络在处理输入时能够执行的操作序列的长度有关。这种观点--一个执行顺序操作以完成任务的深度网络--对于习惯于将算法视为“找到人的边界,寻找边界上方的头部,寻找头部内的嘴巴”等操作序列的软件开发人员可能是迷人的。
跳过连接
深度带来了一些额外的挑战,这些挑战阻碍了深度学习模型在 2015 年之前达到 20 层或更多层。增加模型的深度通常会使训练更难收敛。让我们回顾反向传播,并在非常深的网络环境中思考一下。损失函数对参数的导数,特别是早期层中的导数,需要乘以许多其他数字,这些数字来自于损失和参数之间的导数操作链。这些被乘以的数字可能很小,生成越来越小的数字,或者很大,由于浮点近似而吞噬较小的数字。归根结底,长链的乘法将使参数对梯度的贡献消失,导致该层的训练无效,因为该参数和类似的其他参数将无法得到适当更新。
2015 年 12 月,Kaiming He 和合著者提出了残差网络(ResNets),这是一种使用简单技巧的架构,使得非常深的网络能够成功训练( arxiv.org/abs/1512.03385)。该工作为从几十层到 100 层深度的网络打开了大门,超越了当时计算机视觉基准问题的最新技术。我们在第二章中使用预训练模型时遇到了残差网络。我们提到的技巧是:使用跳跃连接来绕过一组层,如图 8.11 所示。

图 8.11 我们具有三个卷积层的网络架构。跳跃连接是NetRes与NetDepth的区别所在。
跳跃连接只是将输入添加到一组层的输出中。这正是在 PyTorch 中所做的。让我们向我们简单的卷积模型添加一层,并让我们使用 ReLU 作为激活函数。带有额外一层的香草模块如下所示:
# In[51]:
class NetDepth(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.conv3 = nn.Conv2d(n_chans1 // 2, n_chans1 // 2,
kernel_size=3, padding=1)
self.fc1 = nn.Linear(4 * 4 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.relu(self.conv1(x)), 2)
out = F.max_pool2d(torch.relu(self.conv2(out)), 2)
out = F.max_pool2d(torch.relu(self.conv3(out)), 2)
out = out.view(-1, 4 * 4 * self.n_chans1 // 2)
out = torch.relu(self.fc1(out))
out = self.fc2(out)
return out
向这个模型添加一个类 ResNet 的跳跃连接相当于将第一层的输出添加到第三层的输入中的forward函数中:
# In[53]:
class NetRes(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.conv3 = nn.Conv2d(n_chans1 // 2, n_chans1 // 2,
kernel_size=3, padding=1)
self.fc1 = nn.Linear(4 * 4 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.relu(self.conv1(x)), 2)
out = F.max_pool2d(torch.relu(self.conv2(out)), 2)
out1 = out
out = F.max_pool2d(torch.relu(self.conv3(out)) + out1, 2)
out = out.view(-1, 4 * 4 * self.n_chans1 // 2)
out = torch.relu(self.fc1(out))
out = self.fc2(out)
return out
换句话说,我们将第一个激活的输出用作最后一个的输入,除了标准的前馈路径。这也被称为恒等映射。那么,这如何缓解我们之前提到的梯度消失问题呢?
想想反向传播,我们可以欣赏到在深度网络中的跳跃连接,或者一系列跳跃连接,为深层参数到损失创建了一条直接路径。这使得它们对损失的梯度贡献更直接,因为对这些参数的损失的偏导数有机会不被一长串其他操作相乘。
已经观察到跳跃连接对收敛特别是在训练的初始阶段有益。此外,深度残差网络的损失景观比相同深度和宽度的前馈网络要平滑得多。
值得注意的是,当 ResNets 出现时,跳跃连接并不是新鲜事物。Highway 网络和 U-Net 使用了各种形式的跳跃连接。然而,ResNets 使用跳跃连接的方式使得深度大于 100 的模型易于训练。
自 ResNets 出现以来,其他架构已经将跳跃连接提升到了一个新水平。特别是 DenseNet,提出通过跳跃连接将每一层与数个下游层连接起来,以较少的参数实现了最先进的结果。到目前为止,我们知道如何实现类似 DenseNets 的东西:只需将早期中间输出算术地添加到下游中间输出中。
在 PyTorch 中构建非常深的模型
我们谈到了在卷积神经网络中超过 100 层。我们如何在 PyTorch 中构建该网络而不至于在过程中迷失方向?标准策略是定义一个构建块,例如(Conv2d,ReLU,Conv2d) + 跳跃连接块,然后在for循环中动态构建网络。让我们看看实践中是如何完成的。我们将创建图 8.12 中所示的网络。

图 8.12 我们带有残差连接的深度架构。在左侧,我们定义了一个简单的残差块。如右侧所示,我们将其用作网络中的构建块。
我们首先创建一个模块子类,其唯一任务是为一个块提供计算--也就是说,一组卷积、激活和跳跃连接:
# In[55]:
class ResBlock(nn.Module):
def __init__(self, n_chans):
super(ResBlock, self).__init__()
self.conv = nn.Conv2d(n_chans, n_chans, kernel_size=3,
padding=1, bias=False) # ❶
self.batch_norm = nn.BatchNorm2d(num_features=n_chans)
torch.nn.init.kaiming_normal_(self.conv.weight,
nonlinearity='relu') # ❷
torch.nn.init.constant_(self.batch_norm.weight, 0.5)
torch.nn.init.zeros_(self.batch_norm.bias)
def forward(self, x):
out = self.conv(x)
out = self.batch_norm(out)
out = torch.relu(out)
return out + x
❶ BatchNorm 层会抵消偏差的影响,因此通常会被省略。
❷ 使用自定义初始化。kaiming_normal_ 使用正态随机元素进行初始化,标准差与 ResNet 论文中计算的一致。批量归一化被初始化为产生初始具有 0 均值和 0.5 方差的输出分布。
由于我们计划生成一个深度模型,我们在块中包含了批量归一化,因为这将有助于防止训练过程中梯度消失。我们现在想生成一个包含 100 个块的网络。这意味着我们需要做一些严肃的剪切和粘贴吗?一点也不;我们已经有了想象这个模型可能是什么样子的所有要素。
首先,在init中,我们创建包含一系列ResBlock实例的nn.Sequential。nn.Sequential将确保一个块的输出被用作下一个块的输入。它还将确保块中的所有参数对Net可见。然后,在forward中,我们只需调用顺序遍历 100 个块并生成输出:
# In[56]:
class NetResDeep(nn.Module):
def __init__(self, n_chans1=32, n_blocks=10):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.resblocks = nn.Sequential(
*(n_blocks * [ResBlock(n_chans=n_chans1)]))
self.fc1 = nn.Linear(8 * 8 * n_chans1, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.relu(self.conv1(x)), 2)
out = self.resblocks(out)
out = F.max_pool2d(out, 2)
out = out.view(-1, 8 * 8 * self.n_chans1)
out = torch.relu(self.fc1(out))
out = self.fc2(out)
return out
在实现中,我们参数化了实际层数,这对实验和重复使用很重要。此外,不用说,反向传播将按预期工作。毫不奇怪,网络收敛速度要慢得多。它在收敛方面也更加脆弱。这就是为什么我们使用更详细的初始化,并将我们的NetRes训练学习率设置为 3e - 3,而不是我们为其他网络使用的 1e - 2。我们没有训练任何网络到收敛,但如果没有这些调整,我们将一事无成。
所有这些都不应该鼓励我们在一个 32×32 像素的数据集上寻求深度,但它清楚地展示了如何在更具挑战性的数据集(如 ImageNet)上实现这一点。它还为理解像 ResNet 这样的现有模型实现提供了关键要素,例如在torchvision中。
初始化
让我们简要评论一下早期的初始化。初始化是训练神经网络的重要技巧之一。不幸的是,出于历史原因,PyTorch 具有不理想的默认权重初始化。人们正在努力解决这个问题;如果取得进展,可以在 GitHub 上跟踪(github.com/pytorch/pytorch/issues/18182)。与此同时,我们需要自己修复权重初始化。我们发现我们的模型无法收敛,查看了人们通常选择的初始化方式(权重较小的方差;批量归一化的输出为零均值和单位方差),然后在网络无法收敛时,将批量归一化的输出方差减半。
权重初始化可能需要一个完整的章节来讨论,但我们认为那可能有些过分。在第十一章中,我们将再次遇到初始化,并使用可能是 PyTorch 默认值的内容,而不做过多解释。一旦你进步到对权重初始化的细节感兴趣的程度--可能在完成本书之前--你可能会重新访问这个主题。
8.5.4 比较本节中的设计
我们在图 8.13 中总结了我们每个设计修改的效果。我们不应该过分解释任何具体的数字--我们的问题设置和实验是简单的,使用不同的随机种子重复实验可能会产生至少与验证准确性差异一样大的变化。在这个演示中,我们保持了所有其他因素不变,从学习率到训练的时代数;在实践中,我们会通过变化这些因素来获得最佳结果。此外,我们可能会想要结合一些额外的设计元素。
但是可能需要进行定性观察:正如我们在第 5.5.3 节中看到的,在讨论验证和过拟合时,权重衰减和丢弃正则化,比批量归一化更具有更严格的统计估计解释作为正则化,两个准确率之间的差距要小得多。批量归一化更像是一个收敛助手,让我们将网络训练到接近 100%的训练准确率,因此我们将前两者解释为正则化。
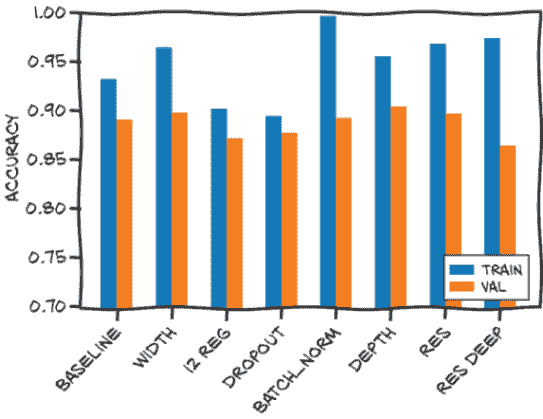
图 8.13 修改后的网络表现都相似。
8.5.5 它已经过时了
深度学习从业者的诅咒和祝福是神经网络架构以非常快的速度发展。这并不是说我们在本章中看到的内容一定是老派的,但对最新和最伟大的架构进行全面说明是另一本书的事情(而且它们很快就会不再是最新和最伟大的)。重要的是我们应该尽一切努力将论文背后的数学精通地转化为实际的 PyTorch 代码,或者至少理解其他人为了相同目的编写的代码。在最近的几章中,您已经希望积累了一些将想法转化为 PyTorch 中实现模型的基本技能。
8.6 结论
经过相当多的工作,我们现在有一个模型,我们的虚构朋友简可以用来过滤她博客中的图像。我们所要做的就是拿到一张进入的图像,裁剪并调整大小为 32 × 32,看看模型对此有何看法。诚然,我们只解决了问题的一部分,但这本身就是一段旅程。
我们只解决了问题的一部分,因为还有一些有趣的未知问题我们仍然需要面对。其中一个是从较大图像中挑选出鸟或飞机。在图像中创建物体周围的边界框是我们这种模型无法做到的。
另一个障碍是当猫弗雷德走到摄像头前会发生什么。我们的模型会毫不犹豫地发表关于猫有多像鸟的观点!它会高兴地输出“飞机”或“鸟”,也许概率为 0.99。这种对远离训练分布的样本非常自信的问题被称为过度泛化。当我们将一个(假设良好的)模型投入生产中时,我们无法真正信任输入的情况下,这是主要问题之一(遗憾的是,这是大多数真实世界案例)。
在本章中,我们已经在 PyTorch 中构建了合理的、可工作的模型,可以从图像中学习。我们以一种有助于我们建立对卷积网络直觉的方式来做到这一点。我们还探讨了如何使我们的模型更宽更深,同时控制过拟合等影响。虽然我们仍然只是触及了表面,但我们已经比上一章更进一步了。我们现在有了一个坚实的基础,可以面对在深度学习项目中遇到的挑战。
现在我们熟悉了 PyTorch 的约定和常见特性,我们准备着手处理更大的问题。我们将从每一章或两章呈现一个小问题的模式转变为花费多章来解决一个更大的、现实世界的问题。第 2 部分以肺癌的自动检测作为一个持续的例子;我们将从熟悉 PyTorch API 到能够使用 PyTorch 实现整个项目。我们将在下一章开始从高层次解释问题,然后深入了解我们将要使用的数据的细节。
8.7 练习
-
更改我们的模型,使用
kernel_size=5传递给nn.Conv2d构造函数的 5 × 5 内核。-
这种变化对模型中的参数数量有什么影响?
-
这种变化是改善还是恶化了过拟合?
-
你能描述
kernel_size=(1,3)会做什么吗? -
这种卷积核会如何影响模型的行为?
-
-
你能找到一张既不含鸟也不含飞机的图像,但模型声称其中有一个或另一个的置信度超过 95%吗?
-
你能手动编辑一张中性图像,使其更像飞机吗?
-
你能手动编辑一张飞机图像,以欺骗模型报告有鸟吗?
-
这些任务随着容量较小的网络变得更容易吗?容量更大呢?
-
8.8 总结
-
卷积可用作处理图像的前馈网络的线性操作。使用卷积可以产生参数更少的网络,利用局部性并具有平移不变性。
-
将多个卷积层及其激活函数依次堆叠在一起,并在它们之间使用最大池化,可以使卷积应用于越来越小的特征图像,从而在深度增加时有效地考虑输入图像更大部分的空间关系。
-
任何
nn.Module子类都可以递归收集并返回其自身和其子类的参数。这种技术可用于计数参数、将其馈送到优化器中或检查其值。 -
函数式 API 提供了不依赖于存储内部状态的模块。它用于不持有参数且因此不被训练的操作。
-
训练后,模型的参数可以保存到磁盘并用一行代码加载回来。
¹PyTorch 的卷积与数学的卷积之间存在微妙的差异:一个参数的符号被翻转了。如果我们情绪低落,我们可以称 PyTorch 的卷积为离散互相关。
² 这是彩票票据假设的一部分:许多卷积核将像丢失的彩票一样有用。参见 Jonathan Frankle 和 Michael Carbin,“The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks,” 2019,arxiv.org/abs/1803.03635。
³ 对于偶数大小的卷积核,我们需要在左右(和上下)填充不同数量。PyTorch 本身不提供在卷积中执行此操作的功能,但函数torch.nn.functional.pad可以处理。但最好保持奇数大小的卷积核;偶数大小的卷积核只是奇数大小的。
⁴ 无法在nn.Sequential内执行此类操作是 PyTorch 作者明确的设计选择,并且长时间保持不变;请参阅@soumith 在github.com/pytorch/pytorch/issues/2486中的评论。最近,PyTorch 增加了一个nn.Flatten层。
⁵ 我们可以从 PyTorch 1.3 开始使用nn.Flatten。
⁶ 由第一个卷积定义的像素级线性映射中的维度在 Jeremy Howard 的 fast.ai 课程中得到强调(www.fast.ai)。
⁷ 在深度学习之外且比其更古老的,将投影到高维空间然后进行概念上更简单(比线性更简单)的机器学习通常被称为核技巧。通道数量的初始增加可以被视为一种类似的现象,但在嵌入的巧妙性和处理嵌入的模型的简单性之间达到不同的平衡。
⁸ 数据加载器有一个pin_memory选项,将导致数据加载器使用固定到 GPU 的内存,目的是加快传输速度。然而,我们是否获得了什么是不确定的,因此我们不会在这里追求这个。
⁹ 我们将重点放在 L2 正则化上。L1 正则化--在更一般的统计文献中因其在 Lasso 中的应用而广为流行--具有产生稀疏训练权重的吸引人特性。
¹⁰ 该主题的开创性论文是由 X. Glorot 和 Y. Bengio 撰写的:“理解训练深度前馈神经网络的困难”(2010 年),介绍了 PyTorch 的Xavier初始化( mng.bz/vxz7)。我们提到的 ResNet 论文也扩展了这个主题,提供了之前使用的 Kaiming 初始化。最近,H. Zhang 等人对初始化进行了调整,以至于在他们对非常深的残差网络进行实验时不需要批量归一化(arxiv.org/abs/1901.09321)。