标签：Autoformer Term 预测 Series 分解 序列 mathcal mathrm

原始题目：Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting
中文翻译：Autoformer:用于长期序列预测的自相关分解变压器
发表时间：2021年
平台：Advances in Neural Information Processing Systems
文章链接：https://proceedings.neurips.cc/paper/2021/hash/bcc0d400288793e8bdcd7c19a8ac0c2b-Abstract.html
开源代码：https://github.com/thuml/Autoformer

摘要

延长预测时间是实际应用的关键需求，如极端天气预警和长期能源消耗规划。本文研究了时间序列的长期预测问题。先验基于变换的模型采用各种自注意机制来发现长程依赖关系。然而，长期未来复杂的时间模式阻碍了模型找到可靠的依赖关系。此外，变压器为了长串联效率，不得不采用稀疏版本的逐点自关注，导致信息利用瓶颈。超越变形金刚，我们将Autoformer设计为一种具有自相关机制的新型分解架构。我们打破了级数分解的预处理惯例，将其作为深度模型的基本内部块进行了更新。这种设计使Autoformer具有复杂时间序列的渐进分解能力。此外，受随机过程理论的启发，我们设计了基于序列周期性的自相关机制，在子序列层面进行相关性发现和表示聚合。自相关在效率和准确性方面都优于自注意。在长期预测中，Autoformer产生了最先进的准确性，在六个基准上相对提高了38%，涵盖了五个实际应用：能源、交通、经济、天气和疾病。代码在此存储库中可用：https://github.com/thuml/Autoformer.

1. 引言

时间序列预测已广泛应用于能源消耗、交通和经济规划、天气和疾病传播预测。在这些现实世界的应用中，一个紧迫的需求是将预测时间延长到遥远的未来，这对长期规划和预警非常有意义。因此，在本文中，我们研究了时间序列的长期预测问题，其特征是预测的时间序列的长度很大。最近的深度预测模型[41，17，20，28，23，29，19，35]取得了很大的进展，尤其是基于Transformer的模型。得益于自关注机制，Transformers在为序列数据建模长期依赖性方面获得了巨大优势，这使得能够建立更强大的大模型[7，11]。

然而，在长期环境下，预测任务极具挑战性。首先，直接从长期时间序列中发现时间相关性是不可靠的，因为相关性可能会被纠缠的时间模式所掩盖。其次，由于序列长度的二次复杂性，具有自注意机制的正则变换器在计算上不适合长期预测。先前基于Transformer的预测模型[41，17，20]主要集中于提高对稀疏版本的自我关注。虽然性能显著提高，但这些模型仍然使用逐点表示聚合。因此，在效率提高的过程中，由于稀疏的逐点连接，它们将牺牲信息利用率，从而成为时间序列长期预测的瓶颈。

为了解释复杂的时间模式，我们试图采用分解的思想，这是时间序列分析的标准方法[1，27]。它可以用于处理复杂的时间序列，并提取更可预测的成分。然而，在预测上下文下，它只能用作过去序列的预处理，因为未来是未知的[15]。这种常见用法限制了分解的能力，并忽略了分解组件之间未来潜在的交互。因此，我们试图超越分解的预处理使用，并提出一种通用架构来赋予深度预测模型以渐进分解的内在能力。此外，分解可以解开纠缠的时间模式，突出时间序列的固有特性[15]。得益于此，我们试图利用序列的周期性来翻新自我关注中的逐点连接。我们观察到，周期之间处于相同相位的子序列往往表现出相似的时间过程。因此，我们试图基于序列周期性导出的过程相似性来构建序列级连接。

基于上述动机，我们提出了一种原始的Autoformer来代替变压器进行长期时间序列预测。Autoformer仍然遵循残差和编码器-解码器结构，但将Transformer更新为分解预测架构。通过嵌入我们提出的分解块作为内部算子，Autoformer可以逐步将长期趋势信息与预测的隐藏变量分离开来。这种设计允许我们的模型在预测过程中交替分解和细化中间结果。受随机过程理论[8，24]的启发，Autoformer引入了一种自相关机制来代替自注意，该机制基于序列的周期性来发现子序列的相似性，并从潜在周期中聚合相似的子序列。该串行机制实现了长度为L的序列的O（L log L）复杂性，并通过将逐点表示聚合扩展到子序列级别来打破信息利用瓶颈。Autoformer在六个基准上实现了最先进的精度。贡献概述如下：

• 为了解决长期未来复杂的时间模式，我们将Autoformer作为一种分解架构，并设计内部分解块，以赋予深度预测模型内在的渐进分解能力。
• 我们提出了一种在序列级别上具有相关性发现和信息聚合的自相关机制。我们的机制超越了以前的自关注家族，可以同时提高计算效率和信息利用率。
• 在六个基准的长期设置下，Autoformer实现了38%的相对改善，涵盖了五个现实世界的应用：能源、交通、经济、天气和疾病。

2. 相关工作

2.1 时间序列预测模型

由于时间序列预测的巨大重要性，各种模型已经得到了很好的发展。许多时间序列预测方法都是从经典工具开始的[32，9]。ARIMA[6，5]通过差分将非平稳过程转换为平稳过程来解决预测问题。滤波方法也用于序列预测[18，10]。此外，递归神经网络（RNN）模型用于对时间序列的时间相关性进行建模[36，26，40，22]。DeepAR[28]将自回归方法和RNN相结合，对未来序列的概率分布进行建模。LSTNet[19]引入了具有递归跳跃连接的卷积神经网络（CNNs），以捕捉短期和长期的时间模式。基于注意力的RNN[39，30，31]引入时间注意力来探索用于预测的长程依赖性。此外，许多基于时间卷积网络（TCN）的工作[34，4，3，29]试图用因果卷积对时间因果关系进行建模。这些深度预测模型主要关注通过递归连接、时间注意或因果卷积进行的时间关系建模。

最近，基于自注意机制的Transformer[35，38]在序列数据方面显示出强大的能力，如自然语言处理[11，7]、音频处理[14]甚至计算机视觉[12，21]。然而，由于记忆和时间中序列长度L的二次复杂性，将自关注应用于长期时间序列预测在计算上是禁止的。LogTrans[20]在Transformer中引入了局部卷积，并提出了LogSparse注意，以选择遵循指数递增区间的时间步长，这将复杂性降低到O（L（log L）2）。Reformer[17]提出了局部敏感哈希（LSH）注意，并将复杂性降低到O（L log L）。Informer[41]扩展了具有基于KL散度的ProbeSparse注意力的Transformer，并实现了O（L log L）复杂性。请注意，这些方法基于vanilla Transformer，并试图将自注意机制改进为稀疏版本，该版本仍然遵循逐点依赖和聚合。在本文中，我们提出的自相关机制基于时间序列的固有周期性，可以提供串行连接。

2.2 时间序列的分解

作为时间序列分析的一种标准方法，时间序列分解[1，27]将时间序列分解为几个组成部分，每个组成部分代表更可预测的模式的基本类别之一。它主要用于探索随时间推移的历史变化。对于预测任务，在预测未来序列[15，2]之前，总是使用分解作为历史序列的预处理，例如具有趋势季节性分解的Prophet[33]和具有基扩展的N-BEATS[23]以及具有矩阵分解的DeepGLO[29]。然而，这种预处理受到历史序列的平面分解效应的限制，并忽视了长期未来序列底层模式之间的层次互动。本文将分解思想从一个新的渐进维度引入。我们的Autoformer将分解作为深度模型的内部块，它可以在整个预测过程中逐步分解隐藏序列，包括过去的序列和预测的中间结果。

3. Autoformer

时间序列预测问题是在给定过去的长度I序列的情况下预测未来最可能的长度-O序列，表示为输入-I-预测-O。长期预测设置是预测长期的未来，即更大的O。如上所述，我们强调了长期序列预测的困难：处理复杂的时间模式，打破计算效率和信息利用的瓶颈。为了解决这两个挑战，我们将分解作为内置块引入深度预测模型，并提出将Autoformer作为分解架构。此外，我们还设计了自相关机制来发现基于周期的依赖关系，并从底层周期中聚合相似的子序列。

3.1 分解架构

我们将Transformer[35]更新为深度分解架构（图1），包括内部串联分解块、自相关机制以及相应的编码器和解码器。

序列分解块 为了学习长期预测环境中复杂的时间模式，我们采用了分解的思想[1，27]，它可以将序列分为趋势周期和季节部分。这两个部分分别反映了该系列的长期进展和季节性。然而，对于未来的系列来说，直接分解是不可行的，因为未来是未知的。为了解决这一困境，我们提出了一个级数分解块作为Autoformer的内部操作（图1），它可以从预测的中间隐藏变量中逐步提取长期平稳趋势。具体地说，我们调整移动平均线来平滑周期性波动，并突出长期趋势。对于长度为L的输入序列\(\mathcal{X}\in\mathbb{R}^{L\times d}\)，过程为：

\[\begin{aligned} &X_{t} =\mathrm{AvgPool}(\mathrm{Padding}(\mathcal{X})) \\ &\mathcal{X}_{\mathbf{s}} ={\mathcal X}-{\mathcal X}_{\mathrm{t}}, \end{aligned}\tag{1} \]

其中\(\mathcal{X}_{\mathrm{s}},\mathcal{X}_{\mathrm{t}}\in\mathbb{R}^{L\times d}\)分别表示季节性部分和提取的趋势周期部分。我们采用AvgPool（·）进行移动平均，并进行填充操作，以保持序列长度不变。我们使用Xs，Xt=SeriesDecomp（X）来总结上述方程，它是一个模型内部块。

模型输入 编码器部分的输入是过去的I时间步长\(\mathcal{X}_{\mathrm{en}}\in\mathbb{R}^{I\times d}\)。作为一种分解架构（图1），Autoformer解码器的输入包含季节部分\(\chi_{\mathrm{des}}\in\mathbb{R}^{(\frac I2+O)\times d}\)和趋势循环部分\(\mathcal{X}_{\mathrm{det}}\in\mathbb{R}^{(\frac{I}{2}+O)\times d}\)。每个初始化由两个部分组成：从编码器输入\(\mathcal{X}_{\mathrm{en}}\)的后半部分分解的长度为\(\frac{I}{2}\)的分量，以提供最近的信息，长度为O的占位符由标量填充。其公式如下：

\[\begin{aligned} \mathcal{X}_{\mathrm{ens}},\mathcal{X}_{\mathrm{ent}}& =\mathrm{SeriesDecomp}(\mathcal{X}_{\mathrm{en}\frac{I}{2}:I}) \\ \mathcal{X}_{\mathrm{des}}& =\mathrm{Concat}(\mathcal{X}_{\mathrm{ens}},\mathcal{X}_{0}) \\ \mathcal{X}_{\mathrm{det}}& =\mathrm{Concat}(\mathcal{X}_{\mathrm{ent}},\mathcal{X}_{\mathrm{Mean}}), \end{aligned}\tag{2} \]

其中\(\mathcal{X}_{\mathrm{ens}},\mathcal{X}_{\mathrm{ent}}\in\mathbb{R}^{\frac{I}{2}\times d}\)分别表示\(\chi_{\mathrm{en}}\)的季节性和趋势性循环部分，\(\mathcal{X}_{0},\mathcal{X}_{\mathrm{Mean}}\in\mathbb{R}^{O\times d}\)分别代表用零填充的占位符和Xen的平均值。

图1：Autoformer架构。编码器通过序列分解块（蓝色块）消除了长期趋势循环部分，并专注于季节模式建模。解码器逐步累积从隐藏变量中提取的趋势部分。来自编码器的过去季节信息由编码器-解码器自相关（解码器中的中心绿色块）使用。

编码器 如图1所示，编码器专注于季节性零件建模。编码器的输出包含过去的季节性信息，并且将被用作交叉信息以帮助解码器细化预测结果。假设我们有N个编码器层。第l个编码器层的总体方程总结为\(\mathcal{X}_{\mathrm{en}}^{l}=\mathrm{Encoder}(\mathcal{X}_{\mathrm{en}}^{l-1})\)。具体如下：

\[\begin{aligned}\mathcal{S}_{\text{en}}^{l,1},_{-}&=\text{SeriesDecomp}\Big(\text{Auto-Correlation}(\mathcal{X}_{\text{en}}^{l-1})+\mathcal{X}_{\text{en}}^{l-1}\Big)\\\mathcal{S}_{\text{en}}^{l,2},_{-}&=\text{SeriesDecomp}\Big(\text{FeedForward}(\mathcal{S}_{\text{en}}^{l,1})+\mathcal{S}_{\text{en}}^{l,1}\Big),\end{aligned}\tag{3} \]

其中"_"是已消除的趋势部分。\(\mathcal{X}_{\mathrm{en}}^{l}=\mathcal{S}_{\mathrm{en}}^{l,2},l\in\{1,\cdots,N\}\)表示第l个编码器层的输出，\(\mathcal{X}_{\mathrm{en}}^{0}\)是嵌入的\(\mathcal{X}_{\mathrm{en}}\)。\(\mathcal{S}_{\mathrm{en}}^{l,i},i\in\{1,2\}\)分别表示第l层中第i个级数分解块之后的季节分量。我们将在下一节中详细描述Auto-Correlation（·），它可以无缝地取代自我关注。

解码器 解码器包括两个部分：趋势周期分量的累积结构和季节分量的堆叠自相关机制（图1）。每个解码器层都包含内部自相关和编码器-解码器自相关，它们可以分别细化预测和利用过去的季节信息。请注意，该模型在解码器过程中从中间隐藏变量中提取潜在趋势，使Autoformer能够逐步细化趋势预测，并消除干扰信息，以便在自相关中发现基于周期的相关性。假设有M个解码器层。利用来自编码器的潜在变量\(\mathcal{X}_{\mathrm{en}}^{N}\)，第l解码器层的方程可以概括为\(\mathcal{X}_{\mathrm{de}}^{l}=\mathrm{Decoder}(\mathcal{X}_{\mathrm{de}}^{l-1},\mathcal{X}_{\mathrm{en}}^{N})\)。解码器可以形式化如下：

\[\begin{aligned} \mathcal{S}_{\mathrm{de}}^{l,1},\mathcal{T}_{\mathrm{de}}^{l,1}& =\text{SeriesDecomp}\Big(\text{Auto-Correlation}(\mathcal{X}_{\mathrm{de}}^{l-1})+\mathcal{X}_{\mathrm{de}}^{l-1}\Big) \\ \mathcal{S}_{\mathrm{de}}^{l,2},\mathcal{T}_{\mathrm{de}}^{l,2}& =\text{SeriesDecomp}\Big(\text{Auto-Correlation}(\mathcal{S}_{\mathrm{de}}^{l,1},\mathcal{X}_{\mathrm{cn}}^{N})+\mathcal{S}_{\mathrm{de}}^{l,1}\Big) \\ \mathcal{S}_{\mathrm{de}}^{l,3},\mathcal{T}_{\mathrm{de}}^{l,3}& =\mathrm{SeriesDecomp}\Big(\mathrm{FeedForward}(\mathcal{S}_{\mathrm{de}}^{l,2})+\mathcal{S}_{\mathrm{de}}^{l,2}\Big) \\ \mathcal{T}_{\mathrm{de}}^{l}& ={\mathcal T}_{\mathrm{de}}^{l-1}+{\mathcal W}_{l,1}*{\mathcal T}_{\mathrm{de}}^{l,1}+{\mathcal W}_{l,2}*{\mathcal T}_{\mathrm{de}}^{l,2}+{\mathcal W}_{l,3}*{\mathcal T}_{\mathrm{de}}^{l,3}, \end{aligned}\tag{4} \]

其中，\(\mathcal{X}_{\mathrm{de}}^{l}=\mathcal{S}_{\mathrm{de}}^{l,3},l\in\{1,\cdots,M\}\)表示第l解码器层的输出。从\(\mathcal{X}_{\mathrm{des}}\)嵌入\(\mathcal{X}_{\mathrm{de}}^{0}\)用于深度变换，\(\mathcal{T}_{\mathrm{de}}^{0}=\mathcal{X}_{\mathrm{det}}\)用于累加。\(\mathcal{S}_{\mathrm{de}}^{l,i},\mathcal{T}_{\mathrm{de}}^{l,i},i\in\{1,2,3\}\)分别表示第l层第i个序列分解块后的季节性分量和趋势周期性分量。\(\mathcal{W}_{l,i},i\in\{1,2,3\}\)表示第i个提取的趋势\(\mathcal{T}_{\mathrm{de}}^{l,i}\)的投影。

图2：自相关（左）和时延聚合（右）。我们利用快速傅立叶变换来计算自相关R（τ），它反映了时延的相似性。然后，基于所选择的延迟τ，将相似的子过程滚动到相同的索引，并通过R（τ）进行聚合。

最终预测是两个精细分解分量的总和，即\({\mathcal W}_{\mathcal S}*{\mathcal X}_{\mathrm{de}}^{M}+{\mathcal T}_{\mathrm{de}}^{M}\)，其中\(\mathcal{W}_{\mathcal{S}}\)是将深度变换的季节分量\(\mathcal{X}_{\mathrm{de}}^{M}\)投影到目标维度。

3.2 自相关机制

如图2所示，我们提出了具有串联连接的自相关机制，以扩大信息利用率。自相关通过计算序列自相关来发现基于周期的相关性，并通过时间延迟聚合来聚合相似的子序列。

基于周期的依赖性可以观察到，周期之间相同的相位位置自然会提供相似的子过程。受随机过程理论[8，24]的启发，对于实离散过程\(\{{\mathcal{X}_{t}}\}\)，我们可以通过以下方程获得自相关\(\mathcal{R}_{\mathcal{X}\mathcal{X}}(\tau)\)：

\[\mathcal{R}_{\mathcal{X}\mathcal{X}}(\tau)=\lim_{L\to\infty}\frac{1}{L}\sum_{t=1}^{L}\mathcal{X}_{t}\mathcal{X}_{t-\tau}.\tag{5} \]

\(\mathcal{R}_{\mathcal{X}\mathcal{X}}(\tau)\)反映了{Xt}与其τ滞后序列{Xt-τ}之间的时延相似性。如图2所示，我们使用自相关R（τ）作为估计周期长度τ的非标准化置信度。然后，我们选择最可能的k周期长度τ1，··，τk。基于周期的依赖性是由上述估计的周期导出的，并且可以通过相应的自相关来加权。

时间延迟聚合基于周期的依赖关系连接估计周期之间的子序列。因此，我们提出了时延聚合块（图2），它可以基于选定的时延τ1，···，τk滚动序列。该操作可以对齐处于估计周期相同相位的相似子序列，这与自关注族中的逐点积聚合不同。最后，我们通过softmax归一化置信度来聚合子序列。

对于长度为L的单头情况和时间序列X，在投影仪之后，我们得到查询Q、密钥K和值V。因此，它可以无缝地取代自注意。自相关机制是：

\[\begin{aligned} \tau_{1},\cdots,\tau_{k}& =\underset{\tau\in\{1,\cdots,L\}}{\arg\text{Topk}}{ ( \mathcal{R}_{\mathcal{Q},\mathcal{K}}(\tau))} \\ \widehat{\mathcal R}_{\mathcal{Q},\mathcal{K}}(\tau_{1}),\cdots,\widehat{\mathcal R}_{\mathcal{Q},\mathcal{K}}(\tau_{k})& =\text{SoftMax}\left(\mathcal{R}_{\mathcal{Q},\mathcal{K}}(\tau_{1}),\cdots,\mathcal{R}_{\mathcal{Q},\mathcal{K}}(\tau_{k})\right) \\ \operatorname{Auto-Correlation}(\mathcal{Q},\mathcal{K},\mathcal{V})& =\sum_{i=1}^{k}\mathrm{Roll}(\mathcal{V},\tau_{i})\widehat{\mathcal{R}}_{Q,\mathcal{K}}(\tau_{i}), \end{aligned}\tag{6} \]

其中arg-Topk（·）是得到Topk自相关的自变量，并且设k=bc×log-Lc，c是超参数。RQ，K是级数Q和K之间的自相关。Roll（X，τ）表示对具有时间延迟τ的X的运算，在此期间，偏移超过第一个位置的元素在最后一个位置重新引入。对于编码器-解码器自相关（图1），K、V来自编码器\(\chi_{\mathrm{en}}\)，并将调整大小为长度O，Q来自解码器的前一块。

图3：自相关与自我关注家庭。全注意力[35]（a）适应所有时间点之间的完全连接。稀疏注意力[17，41]（b）基于所提出的相似性度量来选择点。LogSparse Attention[20]（c）选择遵循指数递增区间的点。自相关（d）侧重于基础时期之间的子序列的连接。

对于Autoformer中使用的多头版本，具有\(d_{model}\)通道的隐藏变量h头，第i头的查询、键和值为\(\mathcal{Q}_{i},\mathcal{K}_{i},\mathcal{V}_{i}\in\mathbb{R}^{L\times\frac{d_{\mathrm{model}}}{h}},i\in\{1,\cdots,h\}\)。过程是：

\[\begin{gathered} \mathrm{MultiHead}(\mathcal{Q},\mathcal{K},\mathcal{V}) =\mathcal{W}_\text{output}*\text{Concat}(\text{head}_1,\cdots,\text{head}_h) \\ \mathrm{where~head}_{i} =\operatorname{Auto-Correlation}(\mathcal{Q}_i,\mathcal{K}_i,\mathcal{V}_i). \end{gathered}\tag{7} \]

高效计算 对于基于周期的依赖关系，这些依赖关系指向处于基础周期相同相位的子进程，并且本质上是稀疏的。在这里，我们选择最可能的延迟，以避免选择相反的相位。因为我们聚合长度为L的O（log L）序列，所以方程6和7的复杂度为O（L log L）。对于自相关计算（方程5），给定时间序列{Xt}，RX X（τ）可以根据Wiener–Khinchin定理[37]通过快速傅立叶变换（FFT）计算：

\[\begin{aligned}\mathcal{S}_{\mathcal{X}\mathcal{X}}(f)&=\mathcal{F}\left(\mathcal{X}_{t}\right)\mathcal{F}^{*}\left(\mathcal{X}_{t}\right)=\int_{-\infty}^{\infty}\mathcal{X}_{t}e^{-i2\pi tf}\mathrm{d}t\overline{\int_{-\infty}^{\infty}\mathcal{X}_{t}e^{-i2\pi tf}\mathrm{d}t}\\\mathcal{R}_{\mathcal{X}\mathcal{X}}(\tau)&=\mathcal{F}^{-1}\left(\mathcal{S}_{\mathcal{X}\mathcal{X}}(f)\right)=\int_{-\infty}^{\infty}\mathcal{S}_{\mathcal{X}\mathcal{X}}(f)e^{i2\pi f\tau}\mathrm{d}f,\end{aligned}\tag{8} \]

其中\(\tau\in\{1,\cdots,L\}\)，F表示FFT，F−1是其逆。*表示共轭运算，并且\(\mathcal{S}_{\mathcal{X}{\mathcal{X}}}({f})\)在频域中。注意，{1，··，L}中所有滞后的序列自相关可以通过FFT同时计算。因此，自相关实现了O（L log L）复杂度。

**自相关与自关注家族 ** 不同于点自关注家族，自相关呈现了串联连接（图3）。具体来说，对于时间依赖性，我们基于周期性找到子序列之间的依赖性。相比之下，自关注族只计算分散点之间的关系。尽管一些自关注[20，41]考虑了局部信息，但它们仅利用这一点来帮助点依赖性发现。对于信息聚合，我们采用时间延迟块来聚合来自底层周期的相似子序列。相比之下，自我关注通过点积来聚合所选的点。自相关具有固有的稀疏性和子序列级表示聚合，可以同时提高计算效率和信息利用率。

4. 实验

我们在六个真实世界的基准上广泛评估了所提出的Autoformer，涵盖了五个主流时间序列预测应用：能源、交通、经济、天气和疾病。

数据集 以下是对六个实验数据集的描述：（1）ETT[41]数据集包含从变压器收集的数据，包括2016年7月至2018年7月期间每15分钟记录一次的负载和油温。（2） Electricity1数据集包含了2012年至2014年321名客户的小时用电量。（3） Exchange[19]记录了1990年至2016年期间八个不同国家的每日汇率。（4） Traffic2是加州交通部每小时收集的数据，描述了旧金山湾区高速公路上不同传感器测量的道路占用率。（5） Weather3在2020年全年每10分钟记录一次，其中包含21个气象指标，如气温、湿度等。（6）ILI4包括2002年至2021年间美国疾病控制和预防中心每周记录的流感样疾病（ILI）患者数据，该数据描述了ILI患者的比例和患者总数。我们遵循标准协议，按照时间顺序将所有数据集划分为训练集、验证集和测试集，ETT数据集的比例为6:2:2，其他数据集的比率为7:1:2。

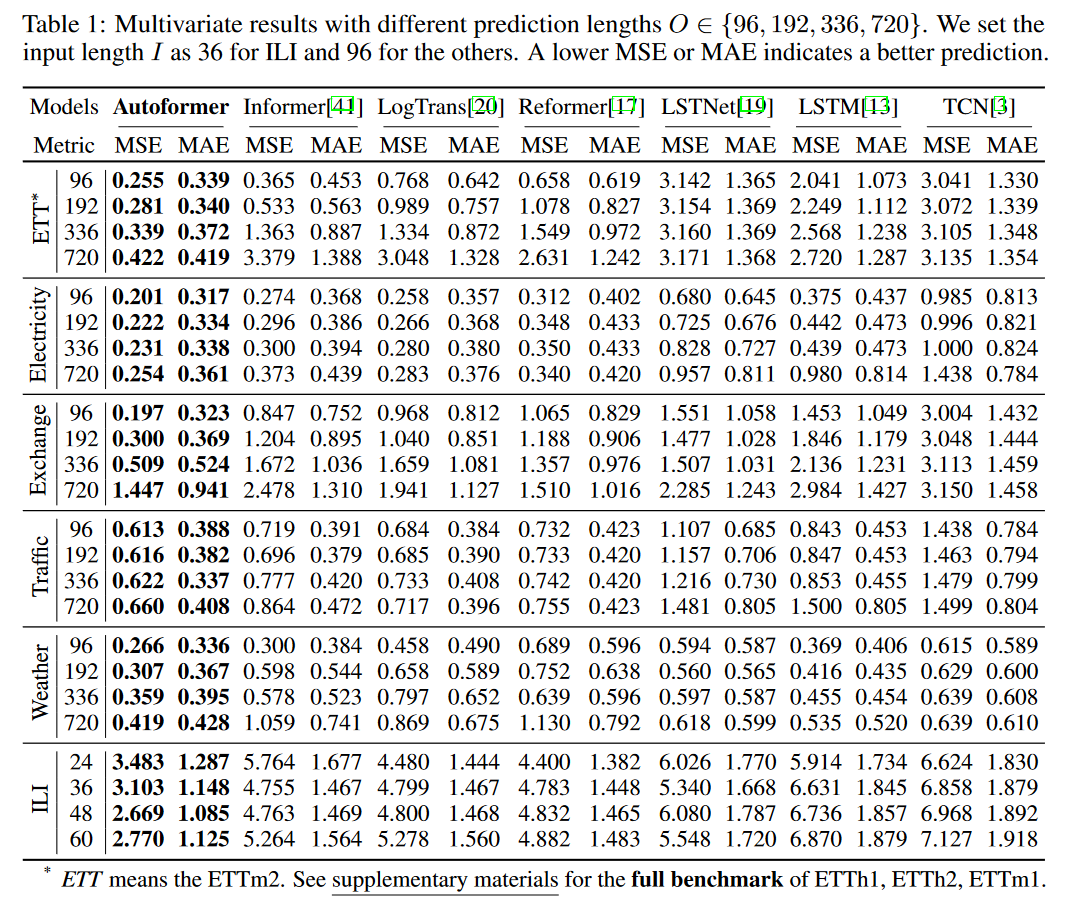
表1：具有不同预测长度O∈{96,192,336,720}的多变量结果。我们将ILI的输入长度I设置为36，将其他的设置为96。较低的MSE或MAE指示更好的预测。

实现细节 我们的方法是用L2损失进行训练的，使用ADAM[16]优化器，初始学习率为10-4。批量大小设置为32。训练过程在10个时期内提前停止。所有实验重复三次，在PyTorch[25]中实现，并在单个NVIDIA TITAN RTX 24GB GPU上进行。自相关的超参数c在1到3的范围内，以权衡性能和效率。标准偏差和灵敏度分析见补充资料。Autoformer包含2个编码器层和1个解码器层。

基线我们包括10种基线方法。对于多变量设置，我们选择了三个最新的基于转换器的模型：Informer[41]、Reformer[17]、LogTrans[20]，以及两个基于RNN的模型：LSTNet[19]、LSTM[13]和基于CNN的TCN[3]作为基线。对于单变量设置，我们包括更具竞争力的基线：N-BEATS[23]、DeepAR[28]、Prophet[33]和ARMIA[1]。

表2：在典型数据集上，具有不同预测长度O∈{96192336720}的单变量结果。我们将输入长度I设置为96。较低的MSE或MAE指示更好的预测。

4.1 主要结果

为了比较不同未来范围下的性能，我们固定输入长度，并评估具有广泛预测长度范围的模型：96192336720。这种设置正好符合长期预测的定义。以下是多变量和单变量设置的结果。

多变量结果 对于多变量设置，Autoformer在所有基准和所有预测长度设置中都实现了一致的最新性能（表1）。特别是，在输入96-预测336设置下，与之前最先进的结果相比，Autoformer给出了74%（1.334→0.339）MSE ETT减少18%（0.280→0.231）在电力方面，61%（1.357→0.509）在交易所，15%（0.733→0.622）和21%（0.455→0.359）。对于ILI的输入36-predict-60设置，Autoformer使43%（4.882→2.770）MSE降低。总体而言，Autoformer在上述设置中产生了38%的平均MSE降低。请注意，Autoformer在没有明显周期性的Exchange数据集中仍然提供了显著的改进。详见补充资料。此外，我们还可以发现，随着预测长度O的增加，Autoformer的性能变化相当稳定。这意味着Autoformer保留了更好的长期鲁棒性，这对现实世界的实际应用有意义，如天气预警和长期能耗规划。

单变量结果 我们在表2中列出了两个典型数据集的单变量结果。与广泛的基线相比，我们的Autoformer在长期预测任务中仍然达到了最先进的性能。特别是，对于输入96-预测336设置，我们的模型实现了14%（0.180→0.145）在具有明显周期性的ETT数据集上的MSE减少。对于没有明显周期性的Exchange数据集，Autoformer超过其他基线17%（0.611→0.508），并显示出更大的长期预测能力。此外，我们发现ARIMA[1]在Exchange数据集的输入-96-预测-96设置中表现最好，但在长期设置中失败。ARIMA的这种情况可以得益于其对非平稳经济数据的固有能力，但受到现实世界序列复杂时间模式的限制。

4.2 消融研究

表3：MSE度量的多变量ETT分解消融。我们的将我们的渐进式架构应用到其他模型中。Sep采用两个模型分别预测预分解的季节性和趋势性周期成分。与Origin相比，Promotion是MSE的减少。

分解架构使用我们提出的渐进分解架构，其他模型可以获得一致的提升，特别是随着预测长度O的增加（表3）。这验证了我们的方法可以推广到其他模型，并释放其他依赖性学习机制的能力，缓解复杂模式造成的分心。此外，我们的体系结构优于预处理，尽管后者使用了更大的模型和更多的参数。特别是，预分解甚至可能带来负面影响，因为它忽略了组件在长期未来的相互作用，如Transformer[35]predict-720，Informer[41]predict-336。

自相关与自注意家族 如表4所示，我们提出的自相关在各种输入-预测-输出设置下实现了最佳性能，这验证了串联连接与点式自注意相比的有效性（图3）。此外，我们还可以观察到，自相关是表4最后一列的记忆效率，可用于长序列预测，如输入-336-预测-1440。

表4：多变量ETT中自相关和自我注意的比较。我们用不同的自注意来代替自形成器中的自相关。“-”表示内存不足。

4.3 模型分析

时间序列分解 如图4所示，如果没有我们的序列分解块，预测模型就无法捕捉季节部分的增长趋势和峰值。通过添加序列分解块，Autoformer可以逐步从序列中聚合和细化趋势周期部分。这种设计也便于学习季节性部分，尤其是波峰和波谷。这验证了我们提出的渐进分解架构的必要性。

图4：最后一个解码器层的学习季节性X M de和趋势周期性T M de的可视化。我们在解码器中从左到右逐渐添加分解块。此案例来自ETT数据集的输入-96-预测-720设置。为了清晰起见，我们将线性增长添加到原始数据中。

依赖性学习 图5（a）中标记的时间延迟大小表示最可能的时间段。我们学习的周期性可以指导模型通过Roll（X，τi），i∈{1，··，6}来聚合来自周期的相同或相邻相位的子序列。在最后一个时间步长（下降阶段），与自我注意相比，自动关联充分利用了所有相似的子序列，没有遗漏或错误。这验证了Autoformer可以更充分、更准确地发现相关信息。

复杂的季节性建模 如图6所示，Autoformer从深度表示中学习的滞后可以指示原始序列的真实季节性。例如，每日记录的Exchange数据集的学习滞后显示了月度、季度和年度（图6（b））。对于每小时记录的交通数据集（图6（c）），学习到的滞后将间隔显示为24小时和168小时，这与真实世界场景的每日和每周时段相匹配 。这些结果表明，Autoformer可以从深度表示中捕捉真实世界序列的复杂季节性，并进一步提供人类可解释的预测。

图5：学习依赖关系的可视化。为了清晰起见，我们选择自相关的前6个时延大小τ1、··、τ6，并将它们标记为原始序列（红线）。对于自我关注，关于最后一个时间步长的前6个相似点（红星）也用橙色点标记。

图6：学习滞后的统计数据。对于测试集中的每个时间序列，我们计算解码器为输入-96-预测-336任务学习的前10个滞后。图（a）-（d）为密度直方图。

**效率分析 ** 我们比较了训练阶段基于自相关和基于自我注意的模型（图7）的运行记忆和时间。所提出的Autoformer在内存和时间上都显示了O（L log L）的复杂性，并实现了更好的长期序列效率。

图7：效率分析。对于内存，我们在Autoformer中将自相关替换为自注意族，并用输入96记录内存。对于运行时间，我们运行自相关或自关注103次，以获得每一步的执行时间。输出长度呈指数级增长。

5. 结论

本文研究了时间序列的长期预测问题，这是现实应用的迫切需求。然而，复杂的时间模式阻碍了模型学习可靠的依赖关系。我们提出了Autoformer作为一种分解架构，通过嵌入序列分解块作为内部算子，它可以从中间预测中逐步聚合长期趋势部分。此外，我们设计了一种高效的自相关机制，在序列级别上进行相关性发现和信息聚合，这与以前的自注意家族形成了鲜明的对比。Autoformer可以自然地实现O（L log L）的复杂性，并在广泛的真实世界数据集中产生一致的最先进的性能。

标签：Autoformer,Term,预测,Series,分解,序列,mathcal,mathrm
From： https://www.cnblogs.com/zhangdoudou/p/18076905