原理图
- 一般pcb板的原理图的电源是恒压源
电路定理
1. 欧姆定理
\[R=\frac{U}{I} \]2.戴维宁定理(电压源等效)
任何一个线性有源二端网络对外都可以等效为一个电压源,其中电压源的电动势是该有源二端网络的开路电压,电压源的内阻是有源二端网络除源后的无源二端网络的等效电阻,这就是戴维宁定理。
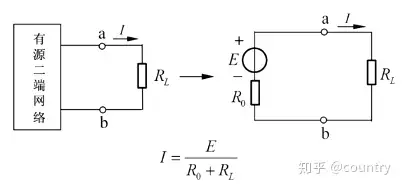
note:现实中,我们遇到大多数电路都是恒压源,所以它在MCU的电路分析中很重
推荐案例:第1章-直流电路分析理论-1.14戴维宁定理 - 知乎 (zhihu.com)
3.诺顿定理(电流源等效)
含独立源的线性电阻单口网络N,就端口特性而言,可以等效为一个电流源和电阻的并联
4. 基尔霍夫定律
KCL:流入电路中某节点的电流之和等于流出电流之和
\[\Sigma_{I_{流入}}=\Sigma_{I_{流出}} \]LVL:闭合回路中电压升之和等于电压降之和
\[\Sigma_{V_{回路}}=0 \]推荐使用的案例 :基尔霍夫定律 - 知乎 (zhihu.com)
5. 电容公式
电压与电流之间的关系
\[u(t_{0})=\frac{q(t_{0})}{C}=\frac{1}{C}\int^{t_{0}}_{-\infty}i(t)dt \cdots 积分公式\\ i(t_0)=C \frac{\mathrm{d} u}{\mathrm{d}{t}}=C \dot{u} \cdots 微分公式 \]电容器:防止电压的突变---从积分公式中可看出
6. 电感公式
\[i(t_0)=-\frac{1}{L}\int^{t_0}_{-\infty}u(t)dt \cdots 积分公式\\ u(t_0)=-L\frac{di}{dt}=-Li^{'} \cdots 微分公式 \]电感器:防止电流的突变---从积分公式中可看出
7. 阻抗
\[Z=R+j\omega L +\frac{1}{j\omega C}=R+j(\omega L - \frac{1}{\omega C}) \]\(\omega=2 \pi f\)是角频率
8. 焦耳定律
在\(t_{0}\)时刻,输入电阻的全部能量是(写成积分形式)
\[W=\int^{t_{0}}_{-\infty}p_tdt=\int^{t_{0}}_{-\infty}u_t i_tdt=R\int^{t_{0}}_{-\infty}i_t^2dt= G\int^{t_{0}}_{-\infty}u_t^2dt \]电阻选型
假设有一个LED灯需要被点亮,LED灯的额定电压\(V_{led}\)和额定电压\(I_{led}\)通过datasheet可以查询,电路中的\(V_{dd}=3.3V\),请问串联多少欧姆电阻?

电阻分到的电压 \(V_{R}=V_{dd}-V_{led}\)
欧姆定律计算电阻 \(R=\frac{V_R}{I_{led}}\)
电池说明
生活中常见的电池电源都是恒压源
常见的电池表示有两个单位:
- 20000\(mAh\)毫安时:在标准电压3.7V的电压下,以20A的电流放电,可以放电一小时
- 74\(Wh\)瓦时:以74W的功率放电,可以放电一小时
已知\(P=UI\),上述两个单位如何转换?U是多少?
对于\(mAh\),有一个假设,在3.7V的标准电压输出下(默认的标准电压,固定值),对于电流的放电速度。
现实中的实例,移动电源(锂电池,20000\(mAh\)),默认其标准电压为3.7V,注意不是输出电压,所以二者的转换公式为
\[74Wh=74000mWh=20000mAh \times 3.7V \]当移动电源的输出电压为5V时,根据其Wh单位,可换算
\[\frac{74Wh}{5V}=\frac{74\times 1000 mWh}{5V}=14800mAh \]继电器
弱点控制强电

用D、E(MCU电路IO的高低电平)控制A、B、C(强电电路)的常闭、常开
三极管&&MOS管
三极管在电路中的作用:
- 开关作用
- 放大作用,放大电信号
NPN三极管&&PNP三级管
P:positive 正极
N:negative 负极
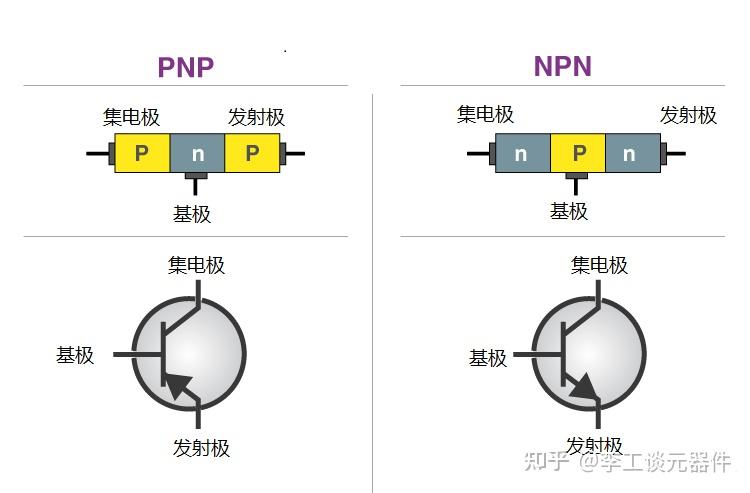
- PNP:当基极为低电压时,电路open,方向为二极管的正向导通(低电压有效)
- NPN:当基极为高电压时,电路opne,方向为二极管的正向导通(高电压有效)
N沟道MOS管&&P沟道MOS管
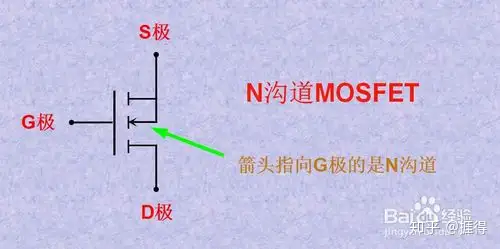
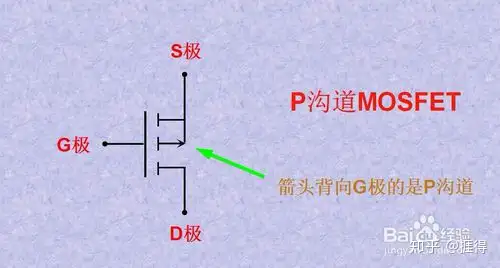
与三极管相比,功耗更小一些
运算放大器(比较器)
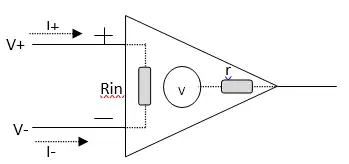
可以理解为:
if(V+>V-)
{
out=v;
}
else
{
out=0;
}