模拟退火，优雅的暴力

我认为有必要摘抄一下提单上的简介

ZX 写的

前言：本片适用于 模拟退火入门-进阶

模拟退火（SA） 是一种 随机化算法。当一个问题的方案数量极大（甚至是无穷的）而且不是一个单峰函数时，我们常使用模拟退火求解。

一般的，很多题都可以用模拟退火水过，在OI界称之 [优雅的暴力]

模拟退火算法入门

先用一句话概括(再借OIWIKI)：模拟退火=如果新状态的解更优则修改答案，否则以一定概率接受新状态

就是先随机出一个答案，如果这个答案是当前最优的就更新最优答案，反之则以一定概率认为这个答案可能更接近最优答案，而接受这个答案

下面是重点：如何 随机出一个答案 和 确定接受新状态的概率（并且要使随机出的答案尽可能接近最优解）

这就要引入一个新概念 退火

退火=固体退火原理，指固体在高温下徐徐冷却的事情

模拟退火的实现也近似固体退火原理，先有三个参数表示初始温度 \(T_0\) ，降温系数 \(d\) ，终止温度 \(T_k\) 。其中 \(T_0\) 是一个比较大的数，\(d\) 是一个非常接近 1 但是小 1 的数， \(T_k\) 是一个接近0的正数。

先将温度T初始成 \(T_0\) ，每一次将 \(T*=d\) ,直到 \(T\) 到达\(T_k\)

OIwiki的图：![](https://oi-wiki.org/misc/images/simulated-annealing.gif)

现在我们开始解决如何 随机出一个答案 和 确定接受新状态的概率

1. 随机出一个答案：根据题目而变，但一般是随机出的，但是和简单的随机不同，这个答案一般是根据先有的解（注意，不一定是最优解，因为有一定概率我们接受了一个可能更接近最优答案的答案），在此基础随机出的

2. 确定接受新状态的概率：一般比较固定,常见写法是 if (exp(-delta（随机出一个答案-当前最优解） / t（当前温度）) > (double)rand() / RAND_MAX;)接受新状态

模拟退火算法进阶

1. 关于参数

模拟退火的参数基本上决定了代码的准确性，一般的， \(T_0\) 越高， \(T_k\) 越低（ \(T_k >0\) ），\(d\) 越接近 \(1\) ，模拟退火越准确， 但时间越长，建议在写模拟退火是要卡卡参数

2. 关于随机数

模拟退火的精髓就在随机数上，随机数的随机性，循环周期基本上决定了准确度，随机性差，循环周期短的很可能将模拟退火卡掉，建议参考这来优化随机数

3. 关于时间

模拟退火是一个不太稳定的算法 （谁叫他随机），单次可能找不到最优解，一般的要多次运行，有一个 clock() 函数，返回程序运行时间，建议在不超时的情况下尽可能多跑

一般的，可以这样while ((double)clock()/CLOCKS_PER_SEC < MAX_TIME（一个小于时限的参数）) SA()（进行模拟退火）;

模拟退火算法例题

计算几何(基本思想：在当前点上尝试)

• P1337 [JSOI2004]平衡点 / 吊打XXX
• P5544 [JSOI2016]炸弹攻击1
• P4035 [JSOI2008]球形空间产生器(注意精度)
• P4703 偷上网
• CF2C Commentator problem
• P4274 [NOI2004] 小H的小屋
• SP4587 FENCE3 - Electric Fences

最优序列(基本思想：在当前序列上重新构造)

• P3936 Coloring
• P2503 [HAOI2006]均分数据
• P2538 [SCOI2008]城堡
• P3878 [TJOI2010]分金币
• P4966 基地建设

其他(一般是数据太水的)

• P4360 [CEOI2004]锯木厂选址

• P1742 最小圆覆盖 (注意精度)

  其他（参考文献等）

  广告1：如果你没有学习过模拟退火，看这里

广告2：如果你没有学习过模拟退火，看这里

更新日志

2021：08：05 更正 P4360 数据过水，且正解非退火

补充

这个图非常形象的展现了模拟退火的精髓，仔细看，这个图中有多个峰值，而红色的线正是逐个跑到峰值上来回判断。

我们先来讲最基础的模拟退火，也就是动图上的二维平面。

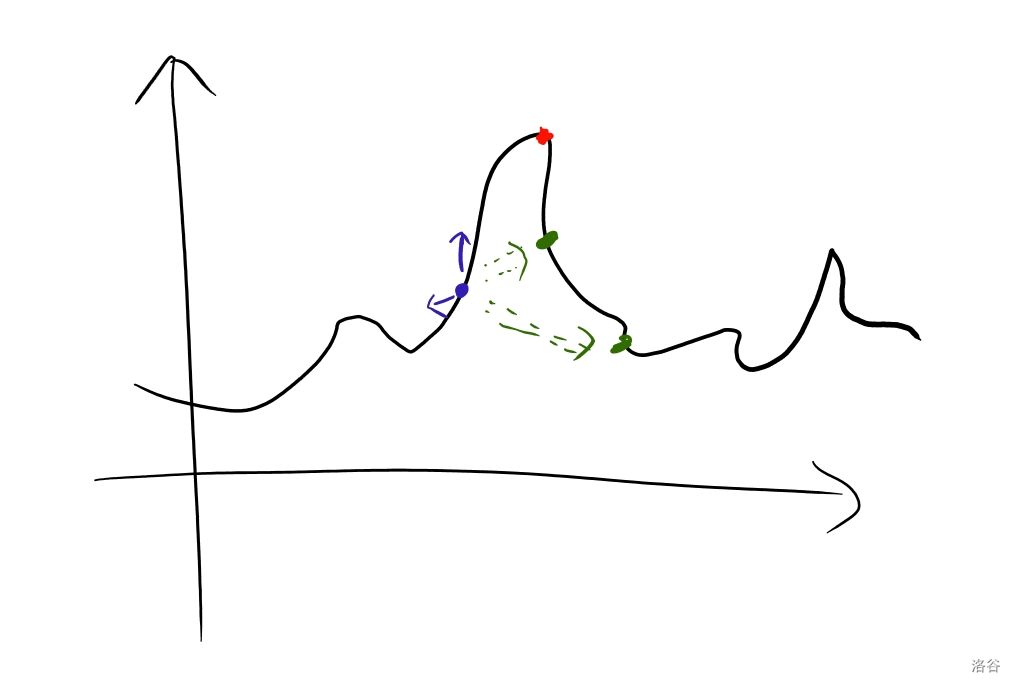
如图，这是一个有多峰值的图，我们要找到峰值最高的，也就是红点。

那么，我们在一开始，会随机到一个点（蓝点），此时它有两种方式，一个是向两边扩散（分别是箭头的方向，哪边大就走哪边，这是贪心策略），另一种是随机到一个点，例如，它可以直接瞬移随机到别的点（绿）。在这两种方法之间，便是 随机出一个答案 和 确定接受新状态的概率。然后使答案更接近最优解。

退火，是一个物理上的名词，过程的话，见上面：

先有三个参数表示初始温度 \(T_0\) ，降温系数 \(d\) ，终止温度 \(T_k\) 。其中 \(T_0\) 是一个比较大的数，\(d\) 是一个非常接近 1 但是小 1 的数， \(T_k\) 是一个接近0的正数。先将温度T初始成 \(T_0\) ，每一次将 \(T*=d\) ,直到 \(T\) 到达\(T_k\)

对于具体操作，上面讲的也比较详细。

主要说说，模拟退火应用场景。

主要分几种情况

• 几何，求距离类问题
• Dp，贪心，在转移 DP，或者在 贪心部分，使用模拟退火来解决。
• 瞎搞

随机化的技巧，对于这个还是有一些帮助的 ：https://oi-wiki.org//misc/random/。我也没自己细看，反正就是用一些科技，一般拍拍子，是不用的，但是模拟退火却很注重随机化的平均，均匀。

就像，洛谷P1337，某人使用高科技rand，只跑了一次模拟退火，就过了，而我，还 while …… 到时限停止，来退火，虽然过了，但是是同样的代码交很多遍才过。

例题

P1337 [JSOI2004]平衡点 / 吊打XXX

对于这个题，就是模拟退火的板子，直接疯狂的模拟退火，然后这相当于是一个二维上的找峰值，之前演示的都是一维。你只需要对于每一个答案，去暴力算一下其贡献，然后不停的模拟退火，这道题为什么可以模拟退火呢？
在一个很大的答案，他周边不可能一下变得很小，最多也是变小一点，甚至有可能变大，所以只一个多峰值的。
PS：通过调整参数，调整步长，来控制模拟退火，挺有趣的，像极了我第一次玩scartch，调整代码参数改变游戏一样。

int n;
struct node{
	double u,v,w;
}a[N],now;
double dist(double x,double y){
	double res=0;
	for(int i=1;i<=n;i++){
		res+=sqrt((x-a[i].u)*(x-a[i].u) + (y-a[i].v)*(y-a[i].v))*a[i].w;
	}return res;
}void sa(){
	now.u=(rand()%10000)*2-10000,now.v=(rand()%10000)*2-10000,now.w=dist(now.u,now.v); 
	for(double T = 1000;T >= 1e-8;T *= 0.99){
		double xx=now.u+((rand()%10000)*2-10000)*T;
		double yy=now.v+((rand()%10000)*2-10000)*T;
		double ww=dist(xx,yy);
		if(ww < now.w) now={xx,yy,ww};
		else if(exp(-(ww-now.w)/T)*RAND_MAX>rand())	now={xx,yy,now.w};		
	}
}
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].u>>a[i].v>>a[i].w;
	
	while((double)clock()/CLOCKS_PER_SEC<0.99) sa();
	printf("%.3lf %.3lf",now.u,now.v);
}

我用的是普通rand，但建议用科技。