首页 > 其他分享 >矩阵乘法与矩阵快速幂

矩阵乘法与矩阵快速幂

时间：2024-02-27 18:02:29浏览次数：24  
标签：begin end int 矩阵 long bmatrix 快速 乘法

矩阵乘法与矩阵快速幂

1 矩阵乘法

1.1 定义

对于两个矩阵 $A,B$，其中 $A$ 大小为 $n\times m$ ，$B$ 大小为 $m\times p$，则这两个矩阵可以做乘法，得到的矩阵 $C$ 的大小为 $n\times p$。

例如：
$$
A=\begin{bmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
\end{bmatrix}\
B=\begin{bmatrix}
b_{11} & b_{12}\
b_{21} & b_{22}\
b_{31} & b_{32}
\end{bmatrix}
$$
则有：
$$
C=AB=\begin{bmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
\end{bmatrix}\begin{bmatrix}
b_{11} & b_{12}\
b_{21} & b_{22}\
b_{31} & b_{32}
\end{bmatrix}=\begin{bmatrix}
a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31} & a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}\
a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31} & a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}
\end{bmatrix}
$$

1.2 注意点

  • 只有当矩阵 $A,B$ 满足 $A$ 的列数等于 $B$ 的行数时，才能进行矩阵乘法。
  • 矩阵乘法不满足交换律（这点很重要）

1.3 代码

提供一个封装模板。

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef long long LL;
const int Maxn = 205;

int n, m, p;

struct matrix {
	int n, m, p[Maxn][Maxn];
	matrix operator * (const matrix &b) const {
		matrix a = *this, c;
		c.n = a.n, c.m = b.m;
		for(int i = 1; i <= a.n; i++) {
			for(int j = 1; j <= a.m; j++) {
				for(int k = 1; k <= b.m; k++) {
					c.p[i][k] += a.p[i][j] * b.p[j][k];
				}
			}
		}
		return c;
	}
	void print() {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= m; j++) {
				cout << p[i][j] << " ";
			}
			cout << '\n';
		}
	}
}A, B, C;

signed main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	A.n = n, A.m = m;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			cin >> A.p[i][j];
		}
	}
	cin >> p;
	B.n = m, B.m = p;
	for(int i = 1; i <= m; i++) {
		for(int j = 1; j <= p; j++) {
			cin >> B.p[i][j];
		}
	}
	C = A * B;
	C.print();
	return 0;
}

2 矩阵快速幂

2.1 定义

仿照着数字的快速幂，我们也能快速求出矩阵的幂。

定义矩阵的幂为：$A^n=A\cdot A\cdot A\cdot A\cdots$

这很明显需要满足原矩阵为正方形。

2.2 用途

矩阵快速幂的经典应用就是加速递推。

直接举几个例子。

2.2.1 「例 1」Fibonacci 第 n 项

Problem

求斐波那契数列第 $n$ 项后四位（$n\le10^9$）

Solution

第一眼：这不是递推板题吗！

然而 $n\le10^9$，$O(n)$ 暴力绝对爆炸。

我们运用矩阵快速幂加速递推。

接下来我们来求一下递推式（注意掌握方法）：

$①$ 我们先来写出 $F_n$ 的部分：
$$
\begin{bmatrix}
F_n \
\
\end{bmatrix}=\begin{bmatrix}
1 & 1\
\ &
\end{bmatrix}\begin{bmatrix}
F_{n-1} \
F_{n-2}
\end{bmatrix}
$$
$②$ 接下来我们关注右边的第二个矩阵，发现他们的下标相差 $1$，因此左边的矩阵应该是 $\begin{bmatrix}
F_n \
F_{n-1}
\end{bmatrix}$ 。

$③$ 最后补全整个式子：
$$
\begin{bmatrix}
F_n \
F_{n-1} \
\end{bmatrix}=\begin{bmatrix}
1 & 1\
1 & 0
\end{bmatrix}\begin{bmatrix}
F_{n-1} \
F_{n-2}
\end{bmatrix}
$$
因此我们对于矩阵 $\begin{bmatrix}
1 & 1\
1 & 0
\end{bmatrix}$ 不断做快速幂，然后乘上 $\begin{bmatrix}
F_{1} \
F_{0}
\end{bmatrix}$ 即可。

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef long long LL;
const int Maxn = 205;

int n, mod;

struct matrix {
	int n, m, p[Maxn][Maxn];
	void init() {
		n = 0, m = 0, memset(p, 0, sizeof p);
	}
	matrix operator * (const matrix &b) const {
		matrix a = *this, c;
		c.init();
		c.n = a.n, c.m = b.m;
		for(int i = 1; i <= a.n; i++) {
			for(int j = 1; j <= a.m; j++) {
				for(int k = 1; k <= b.m; k++) {
					c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % mod) % mod;
				}
			}
		}
		return c;
	}
	matrix operator ^ (const int &o) const {
		matrix res, a = *this; int b = o;
		res.init();
		res.n = res.m = 2;
		res.p[1][1] = res.p[2][2] = 1;
		while(b) {
			if(b & 1) {
				res = res * a;
			}
			a = a * a;
			b >>= 1;
		}
		return res;
	}
	void print() {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= m; j++) {
				cout << p[i][j] << " ";
			}
			cout << '\n';
		}
	}
}A;

signed main() {
	ios::sync_with_stdio(0);
	cin >> n >> mod; 
	A.p[1][1] = A.p[1][2] = A.p[2][1] = 1;
	A.n = A.m = 2;
	A = A ^ (n - 1);
	cout << A.p[1][1];
	return 0;
}

2.2.2 「例 2」P207 迷路

Solution

我们发现如果边权为 $1$ ，那么直接将矩阵 $T$ 次方即可。

但是此时边权不为 $1$，所以不能这样做。

但是我们又会发现这个边权居然最高才 $9$，因此我们考虑一下分层图的思路。

将一个点拆成 $9$ 个点并顺次相连，这样能将边权转化为 $1$。举个例子：

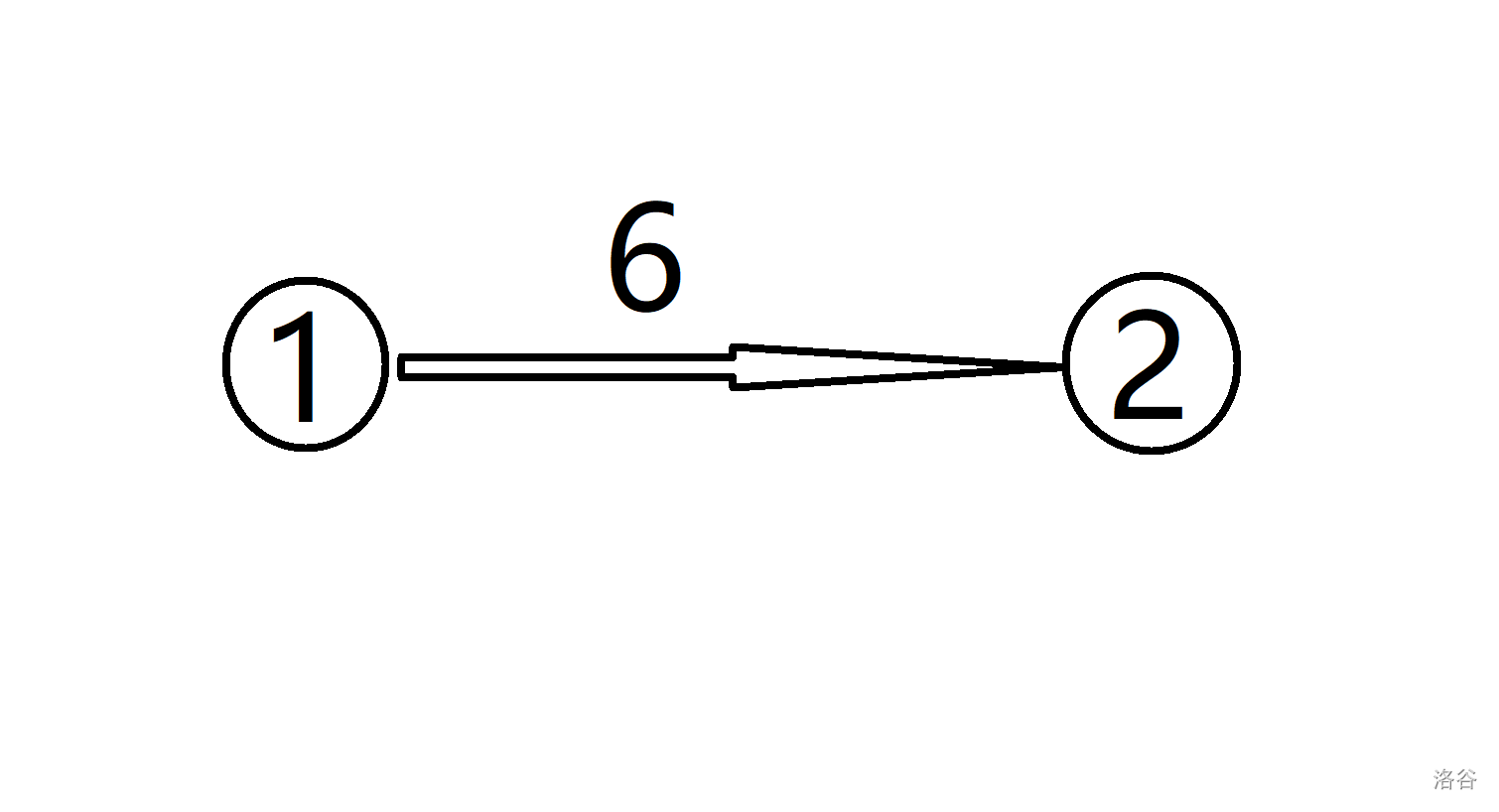
对于这样一条边，我们将 $1$ 和 $2$ 两个点拆开，然后将他们按照原先边权连起来，如下图：

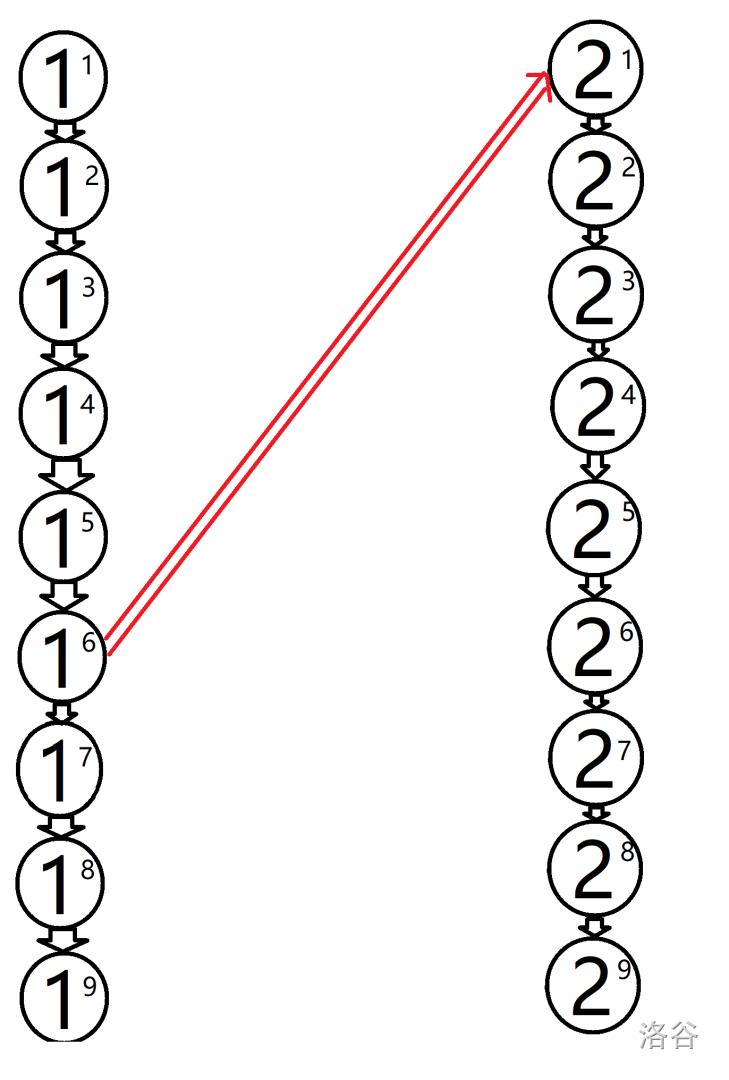
这样从 $1_1$ 走到 $2_1$，经过的边权仍然是 $6$，但我们就转化成了边权为 $1$ 的图。

注意最后统计答案时统计的是点 $n_1$ 的值而非 $n$ 的所有值的和。

接下来注意细节即可。

Code

#include <bits/stdc++.h>

/*
我们发现如果边权为 1，那就是一道求 t 次方的大板子题
然而这题有边权，所以不能这么干
我们考虑分层图的思想，既然边权才 9，那我们直接将一个点暴力拆成九个点，然后边权就能转化为 1
这下就是大板子题了，在求 t 次方即可 
*/

using namespace std;

typedef long long LL;
const int Maxn = 205;
const int Mod = 2009;

int n, t, m;

struct matrix {
	int n, m, p[Maxn][Maxn];
	void init() {
		n = 0, m = 0, memset(p, 0, sizeof p);
	}
	matrix operator * (const matrix &b) const {
		matrix a = *this, c;
		c.init();
		c.n = a.n, c.m = b.m;
		for(int i = 1; i <= a.n; i++) {
			for(int j = 1; j <= a.m; j++) {
				for(int k = 1; k <= b.m; k++) {
					c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % Mod) % Mod;
				}
			}
		}
		return c;
	}
	matrix operator ^ (const int &o) const {
		matrix res, a = *this; int b = o;
		res.init();
		res.n = res.m = a.n;
		for(int i = 1; i <= n; i++) {
			res.p[i][i] = 1;
		}
		while(b) {
			if(b & 1) {
				res = res * a;
			}
			a = a * a;
			b >>= 1;
		}
		return res;
	}
	void print() {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= m; j++) {
				cout << p[i][j] << " ";
			}
			cout << '\n';
		}
	}
}A;

signed main() {
	ios::sync_with_stdio(0);
	cin >> n >> t;
	m = n * 9;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= 8; j++) {
			A.p[9 * (i - 1) + j][9 * (i - 1) + j + 1] = 1;
		}
	}
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) {
			char ch;
			cin >> ch;
			if(ch > '0') {
				A.p[9 * (i - 1) + ch - '0'][9 * (j - 1) + 1] = 1;
			}
		}
	}
	A.n = A.m = m;
	A = A ^ t;
	cout << A.p[1][9 * (n - 1) + 1];
	return 0;
}

2.2.3 「例 3」佳佳的 Fibonacci

Problem

求 $(F_1+2F_2+3F_3+\cdots+nF_n)\bmod{m}$ 的值。

Solution

我们还是运用矩阵快速幂。

但是我们发现这个形式似曾相识，还记得求区间修改区间查询的 BIT 时候的式子吗？他和这个形式是一样的。

我们还是再来推一遍：

先设 $S_i=F_1+F_2+\cdots+F_i$

然后有：
$$
\begin{aligned}原式&=F_1+2F_2+3F_3+\cdots+nF_n\&=n\times S_n-S_{n-1}-S_{n-2}-\cdots-S_1\&=n\times S_n-\sum_{i=1}^{n-1}S_i \end{aligned}
$$
然后我们再令 $P_n=\sum_{i=1}^{n-1}S_i $，则此时原式就可以化为：
$$
n\times S_n-P_n
$$
接下来我们递推 $S_n,P_n$ 来得到原式。

还是分步讨论：

$①$ 写出关于 $P_n$ 的部分。注意到 $P_n=P_{n-1}+S_{n-1}$：

$\begin{bmatrix}
P_n \
\ \
\ \

\end{bmatrix}=\begin{bmatrix}
1 & 1 & 0 & 0\
& & & \
& & & \
& & &
\end{bmatrix}\begin{bmatrix}
P_{n-1} \
S_{n-1} \
\ \

\end{bmatrix}$

$②$ 注意到右边第二个矩阵要满足 $S$ 与 $P$ 下标相等，所以左边还要满足。又注意到 $S_{n}=S_{n-1}+F_n$，所以再补全一部分：

$\begin{bmatrix}
P_n \
S_n \
\ \

\end{bmatrix}=\begin{bmatrix}
1 & 1 & \ &\ \
0 & 1 & 1 &\ \
& & & \
& & &
\end{bmatrix}\begin{bmatrix}
P_{n-1} \
S_{n-1} \
F_n \

\end{bmatrix}$

$③$ 又注意到右边 $F$ 的下标比 $S$ 的下标多 $1$，因此左边应该是 $F_{n+1}$。又注意到 $F_{n+1}=F_n+F_{n-1}$，所以补全为：

$\begin{bmatrix}
P_n \
S_n \
F_{n+1} \
F_n
\end{bmatrix}=\begin{bmatrix}
1 & 1 & 0 & 0 \
0 & 1 & 1 & 0 \
0 & 0 & 1 & 1\
0 & 0 & 1 & 0
\end{bmatrix}\begin{bmatrix}
P_{n-1} \
S_{n-1} \
F_n \
F_{n-1}
\end{bmatrix}$

然后实现即可。

Code

十年 OI 一场空，不开 long long 见祖宗。

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef long long LL;
const int Maxn = 205;

int n, mod;

struct matrix {
	int n, m, p[Maxn][Maxn];
	void init() {
		n = m = 0;
		memset(p, 0, sizeof p);
	}
	void print() {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= m; j++) {
				cout << p[i][j] << " ";
			}
			cout << '\n';
		}
	}
	matrix operator * (const matrix &b) const {
		matrix a = *this, c;
		c.init();
		c.n = a.n, c.m = b.m;
		for(int i = 1; i <= a.n; i++) {
			for(int j = 1; j <= a.m; j++) {
				for(int k = 1; k <= b.m; k++) {
					c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % mod) % mod;
				}
			}
		}
		return c;
	}
	matrix operator ^ (const int &b) const {
		int p = b;
		matrix a = *this, res;
		res.init();
		res.n = res.m = a.n;
		for(int i = 1; i <= a.n; i++) {
			res.p[i][i] = 1;
		}
		while(p) {
			if(p & 1) {
				res = res * a;
			}
			a = a * a;
			p >>= 1;
		} 
		return res;
	}
}A, F;

signed main() {
	ios::sync_with_stdio(0);
	cin >> n >> mod;
	A.init(), F.init();
	A.n = A.m = 4;
	A.p[1][1] = A.p[1][2] = A.p[2][2] = A.p[2][3] = A.p[3][3] = A.p[3][4] = A.p[4][3] = 1;
	F.n = 4, F.m = 1;
	F.p[3][1] = 1;
	A = A ^ n;
	A = A * F;
	cout << (n * A.p[2][1] % mod - A.p[1][1] + mod)	% mod;
	return 0;
}

标签：begin,end,int,矩阵,long,bmatrix,快速,乘法
From： https://www.cnblogs.com/dzbblog/p/18037440

相关文章

  • Hybird App开发，一种快速实现纯血鸿蒙App开发的理念
    2024年1月18日的开发者（HDC）大会上，就官宣了“纯血鸿蒙”操作系统即将于2024年3季度正式投产。与此同时，支付宝、京东、小红书、微博、高德地图、中国移动等在内的超百个头部应用都启动了鸿蒙原生应用开发，鸿蒙开发者日新增注册量已过万，同时众多985、211高校接连开设HarmonyOS相关课程......
  • Python函数每日一讲 - 简洁快速学会globals()函数
    引言在Python中，globals()函数是一个强大的工具，它允许您访问全局命名空间中的所有变量和函数。本文将深入探讨globals()函数的语法、用法以及实际应用场景，帮助大家更好地理解和使用这个函数。语句概览globals()函数的语法如下：globals()函数实例下面是globals()函数......
  • GitHub项目如何快速稳定涨星，让Star飞一会
    GitHub现在已经成了日常开发中必不可少的网站，日常工作和学习中要用到好多上面的开源项目，评价项目质量好坏的一个重要标准就是看Star和Fork的数量，如果看到个Star超过100以上的，基本上这个项目是靠谱的，如果超过1000过，那已经算是很流行了，至于一万以上的，基本上都是如雷贯耳的存在了。......
  • 像闪电般击碎天空吧——快速轻量化模型之 SDXL-Lightning
    SDXL-Lightning是一个由ByteDance（字节跳动）开发的文本到图像的生成模型，其主要贡献在于其高速的生成能力和轻量化的设计。模型的特点快速生成：SDXL-Lightning能够在几步之内生成高质量的1024px图像，这使得它在生成速度上具有优势。这种快速生成的能力使得SDXL-Lightning可以......
  • 如何在三维地球上快速拉白模以辅助建筑规划设计？
       通过以下方法可以在三维地球上快速拉白模以辅助建筑规划设计。 方法/步骤下载三维地图浏览器http://www.geosaas.com/download/map3dbrowser.exe，安装完成后桌面上出现”三维地图浏览器“图标。 2、双击桌面图标打开”三维地图浏览器“ 3、点击“要素标......
  • ES6技巧（快速解构赋值、数组去重、数组转对象）
    1.如何将a,b的值快速互换leta=1;letb=2;[a,b]=[b,a]解析：首先，我们有变量 a 被赋值为 1，变量 b 被赋值为 2。然后，[a,b]=[b,a] 这行代码实际上是将数组 [b,a] 解构赋值给了数组 [a,b]。在解构赋值过程中，右侧的数组 [b,a] 中的值会被依次赋给左侧......
  • 系统设计中的快速估算技巧
    拿到一堆数据，去做架构也好，设计也好，可行性分析也好，工程上需要的是严谨。但是也有很多场景，比如即时的问题争辩和讨论，我们往往需要的是快速、直接的估算，这样的数据显然不需要非常精确，甚至可以说它一定会非常粗略，我们的目标往往只停留在“量级”的级别，但是我们依然可以对方案有......
  • LoRA 微调和低秩矩阵
    LoRA（Low-RankAdaptation）是一种技术，旨在有效调整大型语言模型，以适应特定任务，而无需重新训练整个模型。在论文《LORA:LOW-RANKADAPTATIONOFLARGELANGUAGEMODELS》（https://arxiv.org/abs/2106.09685）中给出了具体方法：通过对模型中的参数进行低秩更新，来实现对大型预训练语言模......
  • Accurately computing running variance —— 已知两个数列各自的均值和方差，如何快速
    原内容来自：https://www.johndcook.com/blog/standard_deviation/计算公式：该种计算方式可以只保存历史数据的平方和，与历史数据的和。相关前文：已知两个数列各自的均值和方差，如何快速求出两个数列拼合后的均值和方差......
  • 已知两个数列各自的均值和方差，如何快速求出两个数列拼合后的均值和方差
    问题：数列A为[1,2,3,4,5,6,7,8,9]，已知数列A的均值和方差和个数为mean_x，var_x，size_x数列B为[20,21,22,23,24,25,26,27,28,29]，已知数列B的均值和方差和个数为mean_y，var_y，size_y现在将数列A与数列B拼合为数列Z，则数列Z为[1,2,3,4,5,6,7,8,9,20,......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99