省流:被吊打了
自己开的一个坑,死也要填完它。
希望我随手写下的笔记对您的学习有所帮助(也不太可能)。
更改日志
2024/01/08:开坑,写了树的直径和换根DP,写不动了(((
2024/01/08 晚上:更新了最小点覆盖和最大独立集,看来精神还可以,顶着明天做手术的风险
2024/01/09:修改错误+增补解释说明(主要在换根DP处)。
学习背景
看着那么多dalao会树型DP,我这个小蒟蒻也来挑战一下。
结果还是被dalao吊打(悲
正片开始
了解树型DP
字面意思,树型DP就是在树上做 DP 或是 DP 过程中有树的特征。树形结构拥有递归特征,所以常以子树作为划分阶段的单位。
树型DP的状态常常形如 DP[u][...] ,表示以 \(u\) 为根的子树……的信息(如最大收益、最小花费等)。
树型DP实现常常采用记忆化搜索,由子节点提供给父节点信息去转移到答案,与 DP 的性质类似(由子节点(子问题)转移到父节点(较大的问题)),也会有父节点为子节点或兄弟节点提供信息的情况。
树的直径
树的直径就是树上最远的两个点之间的距离,连接这两点的路径被称为树的最长链
例题
P2610 [ZJOI2012] 旅游
(别看我一上来就丢出一道紫题,这可是水紫(逃))
题目描述
到了难得的暑假,为了庆祝小白在数学考试中取得的优异成绩,小蓝决定带小白出去旅游~~
经过一番抉择,两人决定将 T 国作为他们的目的地。
T 国的国土可以用一个凸 \(n\) 边形来表示,\(n\) 个顶点表示 \(n\) 个入境/出境口。
T 国包含 \(n-2\) 个城市,每个城市都是顶点均为 \(n\) 边形顶点的三角形(换而言之,城市组成了关于 T 国的一个三角剖分)。两人的旅游路线可以看做是连接 \(n\) 个顶点中不相邻两点的线段。
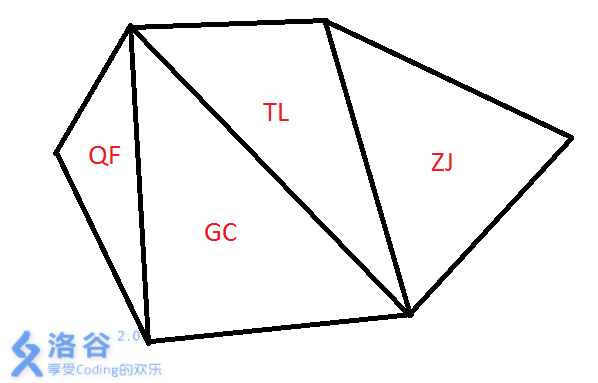
为了能够买到最好的纪念品,小白希望旅游路线上经过的城市尽量多。作为小蓝的好友,你能帮帮小蓝吗?
输入格式
每个输入文件中仅包含一个测试数据。
第一行包含两个由空格隔开的正整数 \(n\),\(n\) 的含义如题目所述。
接下来有 \(n-2\) 行,每行包含三个整数 \(p,q,r\), 表示该城市三角形的三个顶点的编号(T 国的 \(n\) 个顶点按顺时间方向从 \(1\) 至 \(n\) 编号)。
输出格式
输出文件共包含一行,表示最多经过的城市数目。(一个城市被当做经过当且仅当其与线路有至少两个公共点)
说明/提示
对于 \(20\%\) 的数据,\(n\le 2000\)。
对于 \(100\%\) 的数据,\(4\le n \le 200000\)。
解法(怎么感觉开始写题解了)
分析
第一眼看到这题没想到怎么用树型DP,连建图都不会,后面想到可以把一个城市看成一个点,如果两个城市有发生冲突的公共边,就在这两个点之间建一条边。
那怎么知道是不是公共边呢?用个 map 统计就好啦(要先把三个数排序哦!)。
这里是可以确定这是一颗树的,那不就可以树型DP了吗。
那这个要求“旅游路上经过的城市尽量多”就可以抽象为“在树上找一条最长路径”,就可以直接求树的直径了。
那么树的直径又要何去求呢?
其实可以找一个点 \(u\) 作为树根(无根树变为有根树),直径的长度就是从点 \(u\) 出发的最长链长度+从点 \(u\) 出发的次长链长度,就是类似于两条链在点 \(u\) 接上了。
但是不知道点 \(u\) 是哪个点怎么办?其实可以随便找一个点作为根(无根树变为有根树),然后对这棵树进行 DFS 维护每个点的从此点出发的最长链长度和从此点出发的次长链长度,最后取个 max 即可。
设状态
我们设 \(dp_{u,0}\) 为从点 \(u\) 出发的最长链长度, \(dp_{u,1}\) 为从点 \(u\) 出发的次长链长度。
转移
设点 \(u\) 的第 \(i\) 个儿子为点 \(v_{ i}\) ,则有:
-
若 \(dp_{v_i,0}+1 > dp_{u,0}\),说明有更优的最长链,则将当前的最长链
贬变为次长链,再更新最长链,就是 \(dp_{u,1}=dp_{u,0},dp_{u,0}=dp_{v,0}+1\)。 -
再看,若 \(dp_{v_i,0}+1 \le dp_{u,0}\) 且 \(dp_{v_i,0}+1 > dp_{u,1}\),说明有更优的次长链,则将当前的次长链扔掉,再更新次长链,就是 \(dp_{u,1}=dp_{v,0}+1\)。
解
边界为 \(dp_{u,0/1}=0\),目标解为 \(\max(dp_{u,0}+dp_{u,1})\),即每个点的最长链长度+次长链长度的最大值即为答案。
CODE(不就是题解吗):
#include<bits/stdc++.h>
using namespace std;
map<pair<int,int>,int>mp;//记录的map
int n,ret,x,y,z,dp[200010][2];
vector<int>g[200010];
void sort1(int &x,int &y,int &z){//这个不必解释,三个数排序
if(x>y){
swap(x,y);
}if(y>z){
swap(y,z);
}if(x>y){
swap(x,y);
}
}void dfs(int u,int x){
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(v!=x){
dfs(v,u);//先要DFS
if(dp[v][0]+1>dp[u][0]){//转移
dp[u][1]=dp[u][0],dp[u][0]=dp[v][0]+1;
}else if(dp[v][0]+1>dp[u][1]){
dp[u][1]=dp[v][0]+1;
}
}
}ret=max(ret,dp[u][0]+dp[u][1]);//取max
}int main(){
scanf("%d",&n);
for(int i=1;i<=n+2;i++){
scanf("%d%d%d",&x,&y,&z);
sort1(x,y,z);//排序
if(mp[make_pair(x,y)]!=0){//若之前统计到过这条边了
g[i].push_back(mp[make_pair(x,y)]);
g[mp[make_pair(x,y)]].push_back(i);//与之前map里记录的城市建边
}if(mp[make_pair(y,z)]!=0){//同上
g[i].push_back(mp[make_pair(y,z)]);
g[mp[make_pair(y,z)]].push_back(i);
}if(mp[make_pair(x,z)]!=0){//同上
g[i].push_back(mp[make_pair(x,z)]);
g[mp[make_pair(x,z)]].push_back(i);
}mp[make_pair(x,y)]=i,mp[make_pair(y,z)]=i,mp[make_pair(x,z)]=i;//把标记改为这个城市
}dfs(1,-1);
printf("%d",ret+1);//还要加一,就是点(城市)的数量=边的数量+1
return 0;
}
换根DP
2024/01/08:我可能暂时就写这俩了,树的重心还没学会,到时候再写啊。
有一些树型DP中,转移不仅和子树内有关,还有可能和子树外的节点有关(注意这里,后面有考),此时就要二次扫描与换根:
第一次扫描:任选一个点 \(u\) 为根,在这个有根树上进行 DFS,回溯时自底向上转移,由子节点转移父节点,就是普通的一次树型DP。
第二次扫描:以 \(u\) 为根开始对整棵树 DFS ,递归前使用自顶向下更新,用父节点的值更新子节点的值,计算出“换根”后得到的解。
例题
P2986 [USACO10MAR] Great Cow Gathering G
题目描述
Bessie 正在计划一年一度的奶牛大集会,来自全国各地的奶牛将来参加这一次集会。当然,她会选择最方便的地点来举办这次集会。
每个奶牛居住在 \(N\) 个农场中的一个,这些农场由 \(N-1\) 条道路连接,并且从任意一个农场都能够到达另外一个农场。
道路 \(i\) 连接农场 \(A_i\) 和 \(B_i\),长度为 \(L_i\)。集会可以在 \(N\) 个农场中的任意一个举行。另外,每个牛棚中居住着 \(C_i\) 只奶牛。
在选择集会的地点的时候,Bessie 希望最大化方便的程度(也就是最小化不方便程度)。
比如选择第 \(X\) 个农场作为集会地点,它的不方便程度是其它牛棚中每只奶牛去参加集会所走的路程之和(比如,农场 \(i\) 到达农场 \(X\) 的距离是 \(20\),那么总路程就是 \(C_i\times 20\))。
帮助 Bessie 找出最方便的地点来举行大集会。
输入格式
第一行一个整数 \(N\) 。
第二到 \(N+1\) 行:第 \(i+1\) 行有一个整数 \(C_i\)。
第 \(N+2\) 行到 \(2N\) 行:第 \(i+N+1\) 行为 \(3\) 个整数:\(A_i,B_i\) 和 \(L_i\)。
输出格式
一行一个整数,表示最小的不方便值。
提示
\(1\leq N\leq 10^5\),\(1\leq A_i\leq B_i\leq N\),\(0 \leq C_i,L_i \leq 10^3\)。
解法
朴素做法
这题我们可以先来考虑朴素的做法,枚举每一个节点作为集会地点,然后 DFS 统计出不方便程度,接着取 min ,时间复杂度巨大,考虑优化。
设状态
设 \(u\) 的儿子是 \(v_i\)。
设 \(dp_{u}\) 是以 \(u\) 为根的子树中所有节点到点 \(u\) 的不方便程度,\(sum_u\) 是以 \(u\) 为根的子树中奶牛的总只数,\(w\) 是点 \(v_i\) 与点 \(u\) 之间的距离。
转移
可以思考由 \(dp_{v_i}\) 转移至 \(dp_{u}\),发现其实可以直接用 \(dp_{v_i} + sum_{v} \times w\) 就可以转移到 \(dp_u\) 了,代表以 \(v_i\) 为根的子树中所有节点到点 \(v_i\) 的不方便程度 \(+\) 以 \(v_i\) 为根的子树中奶牛的总只数 \(\times\) 点 \(v_i\) 与点 \(u\) 之间的距离。
所以,设 \(u\) 为整棵树的根, \(dp_u = \sum \left( dp_{v_i}+sum_{v_i}\times w \right)\),$sum_u=c_u+ \sum sum_v $ ,就是指点 \(u\) 的奶牛数 \(+\) 点 \(u\) 所有子树中的奶牛数。
解
这样可求出每个点为根时的所有奶牛到此点的不方便程度,最后取 min 即可,时间复杂度 \(\mathcal{O}(n^{2})\)。
二次扫描+换根法
可以看到就算朴素做法就算优化也无法满分,\(\mathcal{O}(n^{2})\) 的时间复杂度在 \(10^{5}\) 的数据下任然会超时,但我们可以继续优化,这就是二次扫描+换根法。
我们可以画一张假设的图:
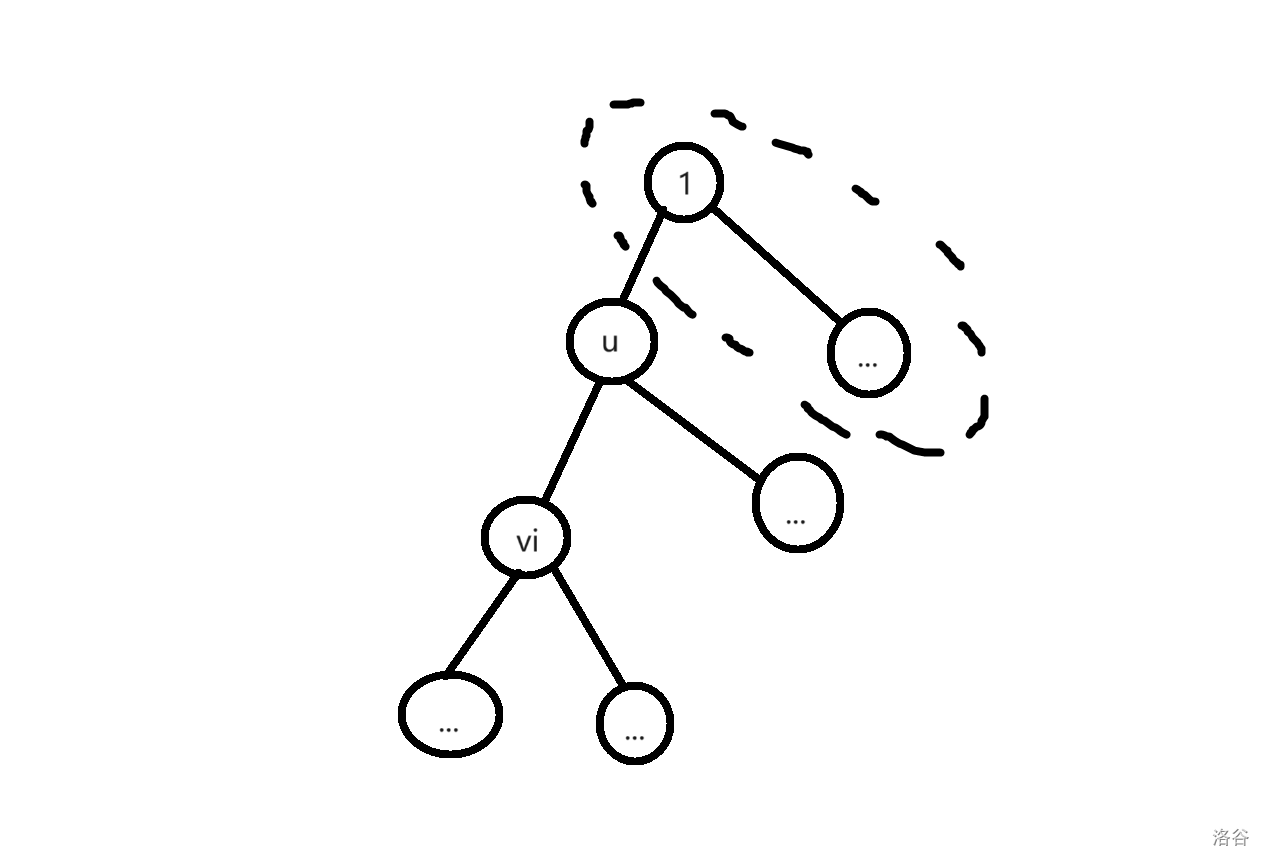
(真的大大小小,画技不好,嫌丑轻喷!)
一次转移
首先 DFS 一遍以 \(u\) 为根的子树,那么结束后 \(dp_u\) 中存的是是以 \(u\) 为根的子树中所有节点到点 \(u\) 的不方便程度,\(sum_u\) 中存的是以 \(u\) 为根的子树中所有节点住的奶牛的总只数
二次转移
根据上面那张图,第一遍 DFS 后 \(dp_u\) 中存的就是除了虚线框出来的节点到点 \(u\) 的不方便程度。
考虑怎么求虚线框出来的所有节点到点 \(u\) 的不方便程度。
其实可以想,虚线框出来的所有节点到点 \(u\) 的不方便程度就是所有虚线框出来的节点到点 \(1\) (就是点 \(u\) 的父节点)的不方便程度 \(+\) 虚线框出来的所有奶牛一起从点 \(1\) 到点 \(u\) 的总不方便值。
设从点 \(1\) 到点 \(u\) 的距离是 \(w\)(根据上面的图, \(1\) 是 \(u\) 的父节点):
-
所有虚线框出来的点到点 \(1\) (就是点 \(u\) 的父节点)的距离就是 \(\left(dp_1-dp_u-sum_u \times w\right)\),代表以点 \(1\) 为根的子树中所有点到点 \(1\) 的不方便值 \(-\) 以点 \(u\) 为根的子树中所有点到点 \(u\) 的不方便值 \(-\) 点 \(u\) 为根的子树中所有奶牛一起从点 \(u\) 到点 \(1\) 的总不方便值(就是以点 \(u\) 为根的子树中的奶牛数 \(\times\) 从点 \(u\) 到点 \(1\) 的距离)。
-
虚线框出来的所有奶牛一起从点 \(1\) 到点 \(u\) 的总不方便值就是 \(\left(sum_1-sum_{u}\right) \times w\),代表以点 \(1\) 为根的子树中的奶牛只数减去以点 \(u\) 为根的子树中的奶牛只数 \(\times\) 点 \(1\) 到点 \(u\) 之间的距离(解释同上朴素算法转移)。
最后将这两个加一下就行了:
\(dp_{u}=dp_{u} + \left(dp_1-dp_{u}-sum_{u} \times w\right)+\left(sum_1-sum_{u}\right) \times w\)。
这里可以推出公式,设 \(u\) 的儿子是 \(v_i\),从 \(u\) 到 \(v_i\) 的距离是 \(w\) (这里的 \(u\) 和上面的 \(u\) 没有任何关系,上面的仅是为了有助于推出公式):
\(dp_{v_i}=dp_{v_i} + \left(dp_u-dp_{v_i}-sum_{v_i} \times w\right)+\left(sum_u-sum_{v_i}\right) \times w\)。
解
这样我们就可以在第二次 DFS 是求出每个节点作为根时,所有奶牛到这个点的不方便程度了,最后答案为 \(\min(dp_{u})\) ,时间复杂度 \(\mathcal{O}(n)\),可以轻松过掉 \(10^{5}\) 的数据。
其实这里的二次扫描就是就是一开始讲二次扫描+换根法时提到的“转移不仅和子树内有关,还有可能和子树外的节点有关”。
二次扫描+换根法CODE(朴素的就不放了):
#include<bits/stdc++.h>
using namespace std;
int n,x,y,z,c[100010];
long long ret,dp[100010],sum[100010];
struct node{
int v,w;
};
vector<node>g[100010];
void dfs(int u,int x){
sum[u]=c[u];
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v,w=g[u][i].w;//v就是儿子,w是距离
if(v!=x){/特判
dfs(v,u);//先回溯,再转移,这就是自底向上
sum[u]+=sum[v];//统计以u为根的子树中的奶牛只数
dp[u]+=dp[v]+sum[v]*w;//先求出以u为根的子树中所有节点到点u的不方便程度和以u为根的子树中所有节点住的奶牛的总只数。
}
}
}void dfs1(int u,int x){
for(int i=0;i<g[u].size();
int v=g[u][i].v,w=g[u][i].w;//同上
if(v!=x){//同上
dp[v]+=(dp[u]-dp[v]-1ll*sum[v]*w)+1ll*(sum[u]-sum[v])*w;//再加上没有加上的(就如上面图片的虚线框出部分)不方便程度
sum[v]=sum[u];//整个的奶牛数
ret=min(ret,dp[v]);//找答案取min
dfs1(v,u);//先转移,再递归,这就是自顶向下
}
}
}int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&c[i]);
}for(int i=1;i<=n-1;i++){
scanf("%d%d%d",&x,&y,&z);
g[x].push_back((node){y,z});//双向建边
g[y].push_back((node){x,z});
}dfs(1,0);//先统计以它为根的子树
ret=dp[1];//设初值
dfs1(1,0);//再统计没统计到的,二次扫描
printf("%lld",ret);
return 0;
}
练习题
P1364 医院设置
题目描述
设有一棵二叉树,如图:
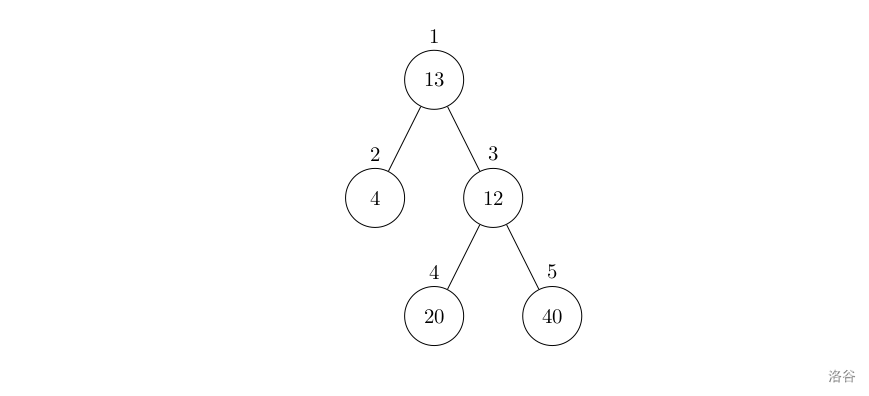
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 \(1\)。如上图中,若医院建在 \(1\) 处,则距离和 \(=4+12+2\times20+2\times40=136\);若医院建在 \(3\) 处,则距离和 \(=4\times2+13+20+40=81\)。
输入格式
第一行一个整数 \(n\),表示树的结点数。
接下来的 \(n\) 行每行描述了一个结点的状况,包含三个整数 \(w, u, v\),其中 \(w\) 为居民人口数,\(u\) 为左链接(为 \(0\) 表示无链接),\(v\) 为右链接(为 \(0\) 表示无链接)。
输出格式
一个整数,表示最小距离和。
提示
数据规模与约定
对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 100\),\(0 \leq u, v \leq n\),\(1 \leq w \leq 10^5\)。
做法
这不就是来送AC的吗
其实可以发现,这题和例题很像,只是点之间的距离是 \(1\),输入还不一样,于是我们就可以直接在代码上改改就过了没有一点难度好吧。
输入怎么改就不需要我说了吧,懂得都懂。
CODE(这还是练习题吗):
#include<bits/stdc++.h>//解释同上
using namespace std;
int n,x,y,z,c[100010];
long long ret,dp[100010],sum[100010];
struct node{
int v,w;
};
vector<node>g[100010];
void dfs(int u,int x){
sum[u]=c[u];
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v,w=g[u][i].w;
if(v!=x){
dfs(v,u);
sum[u]+=sum[v];
dp[u]+=dp[v]+sum[v]*w;
}
}
}void dfs1(int u,int x){
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v,w=g[u][i].w;
if(v!=x){
dp[v]+=(dp[u]-dp[v]-1ll*sum[v]*w)+1ll*(sum[u]-sum[v])*w;
sum[v]=sum[u];
ret=min(ret,dp[v]);
dfs1(v,u);
}
}
}int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&c[i],&x,&y);
if(x!=0){
g[i].push_back((node){x,1});//1代表距离为1,正好就满足了两题的共同点
g[x].push_back((node){i,1});
}if(y!=0){
g[i].push_back((node){y,1});
g[y].push_back((node){i,1});
}
}dfs(1,0);
ret=dp[1];
dfs1(1,0);
printf("%lld",ret);
return 0;
}
最小点覆盖
最小点覆盖是指从图中选出尽量少的点,使得图中所有的边都有和选中的点相连。
设状态
可以这样想:
设 \(dp_{u,0}\) 代表点 \(u\) 被选中了,以点 \(u\) 为根的子树被覆盖时,以点 \(u\) 为根的子树中被选中的点数个数;\(dp_{u,1}\) 代表点 \(u\) 没被选中,以点 \(u\) 为根的子树被覆盖时,以点 \(u\) 为根的子树中被选中的点数个数。
转移
于是,我们可以推到(设 \(u\) 的儿子是 \(v_i\)):
-
\(dp_{u,0}\) 代表点 \(u\) 被选中了,那么所有与点 \(u\) 相连的边都被覆盖了,那么子节点 \(v_i\) 选不选均可,则有 \(dp_{u,0}=dp_{u,0}+min\left(dp_{v_i,0},dp_{v_i,1}\right)\)。
-
\(dp_{u,1}\) 代表点 \(u\) 没被选中,那么所有与点 \(u\) 相连的边都没有被覆盖,为了所有边都被覆盖,那么子节点 \(v_i\) 必须选,则有 \(dp_{u,1}=dp_{u,1}+dp_{v_i,0}\)。
解
设根为 \(rt\),则答案就是 \(\min\left(dp_{rt,0},dp_{rt,1}\right)\)。
例题
P2016 战略游戏
好多绿+的题啊
题目背景
Bob 喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。
题目描述
他要建立一个古城堡,城堡中的路形成一棵无根树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能瞭望到所有的路。
注意,某个士兵在一个结点上时,与该结点相连的所有边将都可以被瞭望到。
请你编一程序,给定一树,帮 Bob 计算出他需要放置最少的士兵。
输入格式
第一行一个整数 \(n\),表示树中结点的数目。
第二行至第 \(n+1\) 行,每行描述每个结点信息,依次为:一个整数 \(i\),代表该结点标号,一个自然数 \(k\),代表后面有 \(k\) 条无向边与结点 \(i\) 相连。接下来 \(k\) 个整数,分别是每条边的另一个结点标号 \(r_1,r_2,\cdots,r_k\),表示 \(i\) 与这些点间各有一条无向边相连。
对于一个 \(n\) 个结点的树,结点标号在 \(0\) 到 \(n-1\) 之间,在输入数据中每条边只出现一次。保证输入是一棵树。
输出格式
输出文件仅包含一个整数,为所求的最少的士兵数目。
提示
数据规模与约定
对于全部的测试点,保证 \(1 \leq n \leq 1500\)。
解法
这不就是最小点覆盖模板题吗??直接套进去就行了!!
就是把放士兵的节点看作选中的点就行了。
CODE(其实可以直接当模板了):
#include<bits/stdc++.h>
using namespace std;
int n,m,dp[2010][2];
vector<int>g[2010];
void dfs(int u,int x){
dp[u][1]=1;//初始化
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(v==x){//特判
continue;
}dfs(v,u);//自底向上
dp[u][0]+=dp[v][1];//可爱的转移,解释见上文
dp[u][1]+=min(dp[v][0],dp[v][1]);
}
}int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int u,v,k;
scanf("%d%d",&u,&k);
for(int j=1;j<=k;j++){//这题建图有点奇怪……
scanf("%d",&v);
g[u].push_back(v);
g[v].push_back(u);
}
}dfs(0,-1);
printf("%d",min(dp[0][0],dp[0][1]));
return 0;
}
最大独立集
最小点覆盖是指从图中选出尽量多的点,使得这些点之间没有边相连。
设状态
设 \(dp_{u,0}\) 代表点 \(u\) 被选中了,以点 \(u\) 为根的子树中被选中的点数个数;\(dp_{u,1}\) 代表点 \(u\) 没被选中,以点 \(u\) 为根的子树中被选中的点数个数。
转移
于是,我们可以推到(设 \(u\) 的儿子是 \(v_i\)):
-
\(dp_{u,0}\) 代表点 \(u\) 被选中了,那么子节点 \(v_i\) 不可能被选中,则有 \(dp_{u,0}=\Sigma dp_{v_i,1}\)。
-
\(dp_{u,1}\) 代表点 \(u\) 没被选中,那么子节点 \(v_i\) 选不选均可,则有 \(dp_{u,1}=\Sigma \max\left(dp_{v_i,0},dp_{v_i,1}\right)\)。
解
设根为 \(rt\),则答案就是 \(\max\left(dp_{rt,0},dp_{rt,1}\right)\)。
例题
P1352 没有上司的舞会
众所周知的题目
题目描述
某大学有 \(n\) 个职员,编号为 \(1\ldots n\)。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 \(r_i\),但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入格式
输入的第一行是一个整数 \(n\)。
第 \(2\) 到第 \((n + 1)\) 行,每行一个整数,第 \((i+1)\) 行的整数表示 \(i\) 号职员的快乐指数 \(r_i\)。
第 \((n + 2)\) 到第 \(2n\) 行,每行输入一对整数 \(l, k\),代表 \(k\) 是 \(l\) 的直接上司。
输出格式
输出一行一个整数代表最大的快乐指数。
提示
数据规模与约定
对于 \(100\%\) 的数据,保证 \(1\leq n \leq 6 \times 10^3\),\(-128 \leq r_i\leq 127\),\(1 \leq l, k \leq n\),且给出的关系一定是一棵树。
又是一道模板题,直接套最大独立集模板就行了。
只是这里的选择顶点的价值不再是 \(1\),而是这个人的快乐成都。
CODE(又是可以直接当模板了):
#include<bits/stdc++.h>
using namespace std;
int n,u,v,mx,fa[20010],r[20010],dp[20010][10];
vector<int>g[20010];
void dfs(int u){
dp[u][1]=r[u];//初始化为快乐程度
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
dfs(v);
dp[u][0]+=max(dp[v][0],dp[v][1]);//转移
dp[u][1]+=dp[v][0];
}
}int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&r[i]);
}for(int i=1;i<n;i++){
scanf("%d%d",&u,&v);
fa[u]=1;//标记他有上司
g[v].push_back(u);
}for(int i=1;i<=n;i++){
if(fa[i]==0){//是根
dfs(i);
mx=max(dp[i][0],dp[i][1]);//取max
break;
}
}printf("%d",mx);
return 0;
}
咕咕咕
标签:int,sum,笔记,leq,DP,树型,节点,dp,为根 From: https://www.cnblogs.com/scyqwq/p/18035177