[NOIP2008 提高组] 火柴棒等式
题目描述
给你 \(n\) 根火柴棍,你可以拼出多少个形如 \(A+B=C\) 的等式?等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数(若该数非零,则最高位不能是 \(0\))。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示:
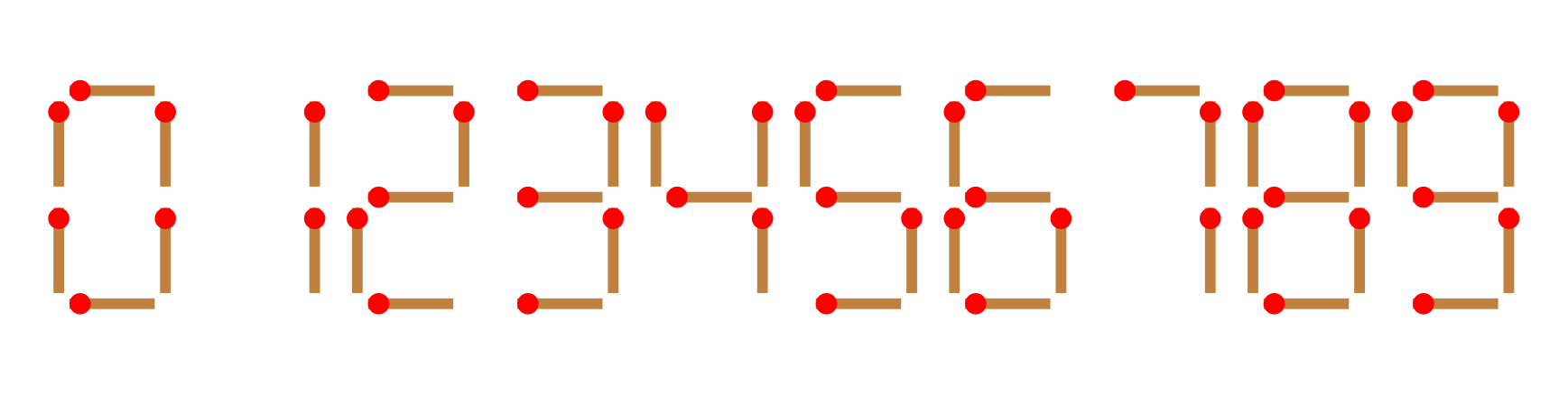
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 \(A\neq B\),则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式(\(A,B,C\geq0\));
- \(n\) 根火柴棍必须全部用上。
输入格式
一个整数 \(n(1 \leq n\leq 24)\)。
输出格式
一个整数,能拼成的不同等式的数目。
样例 #1
样例输入 #1
14
样例输出 #1
2
样例 #2
样例输入 #2
18
样例输出 #2
9
提示
【输入输出样例 1 解释】
\(2\) 个等式为 \(0+1=1\) 和 \(1+0=1\)。
【输入输出样例 2 解释】
\(9\) 个等式为
\(0+4=4\)、\(0+11=11\)、\(1+10=11\)、\(2+2=4\)、\(2+7=9\)、\(4+0=4\)、\(7+2=9\)、\(10+1=11\)、\(11+0=11\)。
noip2008 提高第二题
2.题解
2.1 错误思路:子集枚举
思路
思路错误在只考虑到了每个数位数都是1的情况,然后利用子集枚举选取两个(有重复),三个(无重复)的情况分别进行讨论,若满足条件ans++
但是对于可能存在的两位数情况,过于繁多,无法进行有效讨论,最后废弃
代码
#include <iostream>
using namespace std;
// 定义每个数字所需的火柴棍数量
int matchsticks[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
// 函数用于计算数字num所需的火柴棍数量
int countMatchsticks(int num) {
if (num == 0) return matchsticks[0];
int count = 0;
while (num > 0) {
count += matchsticks[num % 10];
num /= 10;
}
return count;
}
int main() {
int n;
cin >> n;
int totalMatches = 0;
// 统计总共拥有的火柴棍数量
for (int i = 0; i <= 1000; ++i) {
totalMatches += countMatchsticks(i);
}
int count = 0;
// 枚举所有可能的等式
for (int i = 0; i <= 1000; ++i) {
for (int j = 0; j <= 1000; ++j) {
int k = i + j;
// 如果三个数所需的火柴棍数量之和等于n减去加号和等号的火柴棍数量
if (countMatchsticks(i) + countMatchsticks(j) + countMatchsticks(k) == n - 4) {
++count;
}
}
}
cout << count << endl;
return 0;
}
2.2 循环枚举
思路
我上面只考虑了[0,9]几个数组成所需的火柴数,我若是能通过题给范围 0 <= n <= 24, 判断出能组成的最大数是多少,通过循环枚举将范围内所有数所需的火柴数记录下里,再进行判断即可。
考虑极端情况:要使一个数最大,那么另一个加数消耗的火柴数肯定越少越好,同时组成的新的和肯定也要消耗火柴越少越好。
除去我们 + 和 = 所需的四个火柴 n - 4 <= 20
// 定义每个数字所需的火柴棍数量
int matchsticks[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
这里我们观察一下,发现数字1消耗的火柴数最少,所以选择的加数为 1(1111可作为加数也可以作为和),而另一个加数经过判断 20 < 1111 + 1 = 1112(21根火柴) < 1110 + 1 = 1111(22根) 均刚好超过了20根火柴,实际上不会有比这消耗更少火柴棒的情况了,所以只需要讨论[0,1111]内的数即可
代码
#include <iostream>
using namespace std;
// 定义每个数字所需的火柴棍数量
int matchsticks[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
// 函数用于计算数字num所需的火柴棍数量
int countMatchsticks(int num) {
if (num == 0) return matchsticks[0];
int count = 0;
while (num > 0) {
count += matchsticks[num % 10];
num /= 10;
}
return count;
}
int main() {
int n;
cin >> n;
int totalMatches = 0;
// 统计总共拥有的火柴棍数量
for (int i = 0; i <= 1111; ++i) {
totalMatches += countMatchsticks(i);
}
int count = 0;
// 枚举所有可能的等式
for (int i = 0; i <= 1111; ++i) {
for (int j = 0; j <= 1111; ++j) {
int k = i + j;
// 如果三个数所需的火柴棍数量之和等于n减去加号和等号的火柴棍数量
if (countMatchsticks(i) + countMatchsticks(j) + countMatchsticks(k) == n - 4) {
++count;
}
}
}
cout << count << endl;
return 0;
}