大暴力
应用:求解线性方程
前置知识:矩阵操作
对于方程组
\[\begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = m_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = m_2 \\ \cdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = m_n \\ \end{cases} \]我们将他的系数和结果掏出来组成一个\(n \times (n + 1)\)的矩阵来模拟消元操作
目标:把矩阵化成一个上三角的形式
\[\begin{bmatrix} 1 & a_{12}' & a_{13}' & \cdots & a_{1n}' & b_1' \\ 0 & 1 & a_{23}' & \cdots & a_{2n}' & b_2'\\ \cdots \\ & & && 1 & b_n' \end{bmatrix} \]直观理解:
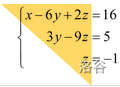
那么我们就能解出\(x_n\),再一步步回代即可
步骤:
eg:
\[\begin{bmatrix}0.02&0.01&0&0&0.02\\2&2&1&0&1\\0&1&2&1&4\\0&0&100&200&800\end{bmatrix} \]枚举待消主元,对于第\(i\)个主元,进行如下操作:
1.找到系数非零行
我们找到当前主元的系数绝对值最大且不为0的行,把他换到第\(i\)行来作为上三角的一部分,然后把剩下行中的该主元消掉,变成
\[\begin{bmatrix}2&2&1&0&1\\0.02&0.01&0&0&0.02\\0&1&2&1&4\\0&0&100&200&800\end{bmatrix} \]2.化简第\(i\)行系数
把主元的系数化为1,方便后续操作
\[\begin{bmatrix}1&1&0.5&0&0.5\\0.02&0.01&0&0&0.02\\0&1&2&1&4\\0&0&100&200&800\end{bmatrix} \]3.消元
枚举后边的行,对于枚举到的第\(k(k \in [i + 1,n])\)行,在上一步的简化下,该行每个系数所减去的值就是该行主元的系数乘上第\(i\)行对应系数得到的值
\[\begin{bmatrix}1&1&0.5&0&0.5\\0.02 - 1 \times0.02&0.01 - 1\times0.02&0 - 0.5\times0.02&0&0.02 - 0.5 \times 0.02\\0&1&2&1&4\\0&0&100&200&800\end{bmatrix} \]依次搞过去就行了,大模拟
特判
-
无解:出现\(0,0,0,\cdots , b_i' \neq 0\)的情况
-
无穷解:上述情况中\(b_i' = 0\)
EXTRA:
异或方程组
取模方程组
P4035 [JSOI2008] 球形空间产生器
设球心\(O(x_1,x_2,\cdots,x_n)\)
对于第\(i,i + 1\)个点而言,满足
\[\sum\limits_{j = 1}^{n}(a_{i,j} - x_j)^2 = \sum\limits_{j = 1}^{n}(a_{i + 1,j} - x_j)^2 \]二次方刚好约掉,化简一下就是
\[\sum\limits_{j = 1}^{n}2(a_{i+1,j} - a_{i,j})x_j = \sum\limits_{j = 1}^{n}(a_{i + 1,j}^2 - a_{i,j}^2) \]\(n + 1\)个点,刚好\(n\)个方程,造就完了
开关问题
已知初始状态\(p_i\),每操作一个开关,与它相关的开关(各开关间的关系给定)也变为相反的状态,求达到目标状态\(q_i\)的方案数
首先有几个点要明确一下
-
结果与顺序无关
-
一个开关只需操作一次(第二次操作会抵消掉第一次操作,相当于没操作)
虽然似乎很显然,但其实挺重要的
我们把关系放到一个矩阵中,\(a_{i,j} = 1\)表示操作开关\(j\)会影响开关\(i\)
这样定义是因为\(j\)表示未知数(主元),\(i\)代表一个方程,矩阵\(a\)相当于是一个系数的角色,所以这么搞
设第\(i\)个开关操作了\(x_i\)次
那么对于第\(i\)个开关来说,他的最终状态就是所有与它有关(包括他自己)的开关操作完后的最终态,即\(a_{i,j} \times x_i\)
接下来考虑用什么运算叠加每一个开关造成的影响
这时有一个性质2来了:所有开关至多操作一次
也就是说:\(\forall x_i,x_i \leqslant 1\)
进一步的,\(a_{i,j} \times x_i\)非\(0\)即\(1\)
结合经验,奇数个操作改变状态,偶数个不改变
所以可以使用异或
那么就得到了
\[\begin{cases}p_1 \oplus a_{11}x_1\oplus a_{12}x_2 \oplus \cdots a_{1n}x_n = q_1\\p_2 \oplus a_{21}x_1\oplus a_{22}x_2 \oplus \cdots a_{2n}x_n=q_2\\ \cdots\\ p_n \oplus a_{n1}x_1\oplus a_{n2}x_2 \oplus \cdots a_{nn}x_n = q_n \end{cases} \]但似乎有一个问题:这样的方程组怎么解呢,它又有几个解(即题目中的方案数)呢?
解法可以参考线性方程组的解法,加(没有减的转化,因为不需要化简系数)改异或,考虑解的数量
对于方程来说只有三种情况:无解,唯一解,无穷解
前两个好说,我们来想想无穷解的内涵
无穷解就是出现了有若干个变量可以取任意值,这些变量通常称为自由元
假设有\(k\)个自由元,结合\(x_i \in\{0,1\}\),那方案数就是这些自由元取值的组合,为\(2^k\)
P2973 [USACO10HOL] Driving Out the Piggies G
设每个节点被污染的概率是\(x_i\),度数是\(d_i\)
古典概型,所以只有加或乘
考虑炸弹如何转移到\(i\)节点
- 节点1:要么瞬间爆炸,要么从别的点转移回来,并且炸弹没炸
- 其他节点:只可能转移而来
但这样太抽象了不像方程组,而且看上去是实时更新的
但是次数没有限制,不可能是遍历若干次后更新更出来的
其实可以这样理解:这些方程是最终态满足的条件
那就解罢
注,严格的证明涉及到期望,先咕咕
一个\(n\times m\),由\(0,1,2\)组成的矩阵,每次操作可以选取一个方格,使得它加上\(2\)之后对\(3\)取模,周围的四个方格加上\(1\)后对\(3\)取模,请你在\(2nm\)操作次数内让整个矩阵变成\(0\)。输出一种方案
其实这个题略微类似于开关问题,只不过那道题模数是\(2\)
先明确这道题中除法统一改为求逆元
设每个方格被修改次数是\(x_{i,j}\),初始值\(a_{i,j}\)
类比开关问题可得:\(x_{i,j} \leqslant 2\)
一个方格受左邻右舍的影响,则有
\[a_{i,j} + 2 \times x_{i,j} + 1 \times(x_{i - 1,j} + x_{i + 1,j} + x_{i,j + 1} + x_{i,j - 1}) \equiv 0 \pmod 3 \]这样一来有个难点:\(x_{i,j}\)如何用一维表示
要不直接开个三维数组吧
对于\(x_{i,j}\),他“头上”的矩形中有\((i - 1) \times m\)个数,他是这一行的第\(j\)个,那他的编号就是\((i - 1) \times m + j\)
接下来构造方案
我想想
对于自由元,直接取零,对于非自由元,移项后再翻成正的,取最终值
搞就完了
(PS:这道题中一个数的逆元就是他自己(doge))
标签:0.02,times,开关,cdots,bmatrix,oplus,高斯消 From: https://www.cnblogs.com/MLP123/p/18017890