【单调栈】
首先我们有一个最简单的方法:\(O(n^3)\) 枚举左右端点,然后再求中间的最小值,最后乘起来得到这段矩形组成的最大面积。
求最小值,我们考虑到ST表,我们可以用它优化到 \(O(n^2)\)。
接下来我们考虑转换枚举思路:
我们发现,一个矩形的大小,由它的左右端点,和它中间的最低高度。
于是我们考虑枚举每一个矩形为最低高度,求这个矩形能往外“扩展”到哪里。
对于我们的矩形 \(x\),其实我们就是求 \(1\sim x-1\) 中最靠近 \(x\) 的比 \(h[x]\) 低的矩形,和右边比 \(h[x]\) 低的矩形。
这就可以用线段树维护,至少为x。
我们顺着上面思考,当一个矩形作为最低点,我们只需要考虑左右两边把这个矩形“拦”下来的地方。
所谓“拦”,就是第一个高度更低的地方。
我们观察到:如果一个矩形高度更低,位置更靠右,那么它就更可能把 \(h[x]\) 拦下来。
换句话说,如果两个矩形 \(i,j\),其中 \(i\) 的高度更高,位置也更左,它就不可能把 \(h[x]\) 拦下来,因为 \(j\) 一定会先拦,而且 \(j\) 拦不下来的 \(i\) 也一定拦不下来。
这个时候我们 \(i\) 就被 \(j\) “完爆” 了。
(完爆更普遍的定义:如果 \(a\) 的各项属性都优于 \(b\),那 \(a\) 完爆 \(b\))
发现到:我们只需要存下所有没有被“完爆”的矩形即可。
按顺序从 \(1\sim n\) 枚举,存下所有不会被“完爆”的矩形。
我们观察到:这些不被完爆的矩形,高度一定是单调递增的。
因为如果有一个不递增了,它之前高度更高的都会被完爆,所以高度更高的一定不会被存下来。
现在我们知道了:我们需要保留所有不被完爆的矩形,并且这些矩形的高度是单调递增的。
接下来我们需要知道:如何保留所有不被完爆的矩形。
用一个类似数学归纳法的想法思考:
我们现在已经把 \(1\sim k\) 的不完爆矩形存下来了,现在加入第 \(k + 1\) 个矩形。
因为第 \(k+1\) 个矩形位置比 \(1\sim k\) 的矩形都更靠右,所以所有高度高于 \(h[k+1]\) 的矩形都会被 \(k+1\) 完爆。
而 \(1\sim k\) 的不完爆矩形是单调的,所以只会有末尾连续几个会被完爆。
把这些被完爆的矩形去掉,然后加入 \(k+1\),就形成了 \(1\sim k+1\) 的不完爆矩形。
因为最末端的反而会先被去掉,所以我们考虑用栈维护。
现在我们知道了:如何保留所有不被完爆的矩形。
接下来我们需要知道:记录不完爆矩形和找左右端点有什么关系。
显然,当我们加入 \(k+1\) 时,第一个不被去掉的矩形就是可以把 \(k+1\) 的左边拦下来的矩形。
同理,我们可以反方向再做一遍这个过程,就可以求出每个矩形右边拦下来的矩形。
【单调(双端)队列】
不妨以求最大值为例。
按照我们的“完爆”思想进行思考:
如果窗口内两个数 \(a[i],a[j]\),满足 \(i<j,a[i]<a[j]\),那么 \(a[i]\) 就被 \(a[j]\) 完爆。
我们只需要在新来的加入时,把所有比新来的小的元素弹出即可。
因为新来的一定在窗口中活的更久,而且新来的更大,所以只要比新来的小,就被新来的完爆。
同理用数学归纳法可知:不完爆数一定是单调递减的。
所以我们考虑维护一个双端队列 \(q\):
(因为左边可能因为时间被弹出,右边的可能会被完爆弹出,要用双端队列)
首先先把 \(q\) 中所有过时的数弹出,因为我们是从左到右扫的,所以要弹的都在左边连续。
然后我们把所有比新来的小的数弹出,因为 \(q\) 中的数是单调递减的,所以比新来的小的都会在右边连续。
注意:我们从窗口里装满了 k 个数时开始输出,注意判断队列是否为空、大小关系。
【应用单调队列优化——多重背包】
首先有一个朴素的思路:一重循环枚举每一类物品,一重循环枚举背包容积,一重循环枚举第 \(i\) 类物体选的个数。
接下来我们考虑优化:
\(dp[i][j]\) 表示前 \(i\) 种物品,恰好 \(j\) 体积的最大价值。
不妨 \(m_i=3,w_i=2\),要求 \(dp[i][j]\)。
\(dp[i][7]\leftarrow dp[i-1][1,3,5,7]\)。
\(dp[i][9]\leftarrow dp[i-1][3,5,7,9]\)。
我们发现,第二维就是一个滑动窗口,每次往右滑 \(w_i\)。
如果 \(v_i=0\),那求 \(dp[i][j]\) 的过程就是用滑动窗口求最大值。
但是,\(v_i\neq 0\),我们细看如何求 \(dp[i][...]\)。
\(dp[i][7]=\max\{dp[i-1][1]+3v_i,dp[i-1][3]+2v_i,dp[i-1][5]+v_i,dp[i-1][7]\}\)。
\(dp[i][9]=\max\{dp[i-1][3]+3v_i,dp[i-1][5]+2v_i,dp[i-1][7]+v_i,dp[i-1][9]\}\)。
这两个东西并不完全就是滑动窗口,但是我们发现一个特点:\(dp[i-1][3,5,7]\) 都有,只是 \(v_i\) 的个数变了,
只要 \(j\) 多了一个 \(w_i\),外面加上的数就少一个 \(v_i\)。
所以我们的 \(j\) 实际上是在一个等差数列上滑动窗口,公差为 \(w[i]\)。
我们只需要枚举首项为 \(0\sim w[i]-1\),然后求出每一种首项的 dp,我们就求完了 \(dp[i][0\sim W]\)。
下面详细讨论如何求一个首项为 \(j\),公差为 \(w[i]\) 的数列答案。
不如把我们要求的设为 \(dp[i][j+k\times w[i]]\)。
\(dp[i][j+k\times w[i]]=\max\{dp[i-1][j+t\times w[i]]+(k-t)\times v[i]\}\).
\(dp[i-1][j+t\times w[i]]+(k-t)\times v[i]=(dp[i-1][j+t\times w[i]] - t\times v[i] + k\times v[i])\)。
而其中 \(k\times v[i]\) 是一个常数,所以我们只要 \(dp[i-1][j+t\times w[i]]-t\times v[i]\) 最大,那么整体就最大。
所以我们的单调队列的判断条件是:若 \(dp[i-1][j+k\times w[i]]-k\times v[i] \geq dp[i-1][j+q.back()\times w[i]]-q.back()\times w[i]\),那么当前队尾就被完爆了。
把所有被完爆的弹出,然后加入 \(k\)。
注意:单调队列里存的是 k,即物品 \(i\) 的使用个数。
然后我们发现:队头的就是使得 \(dp[i-1][j+t\times w[i]]-t\times v[i]\) 最大的 \(t\)。
也就是说,最优的 \(dp[i][j+k\times w[i]]\) 是从 \(t\) 转移过来的。
整理一下思路:
-
初值:因为我们的 dp 设的是 “恰好”,所以初值为 \(-\infty\)。
-
递推:
先一个循环 \(i\leftarrow 1\sim n\),枚举前 \(i\) 种物品。
然后循环 \(j\leftarrow 0\sim w[i]-1\),循环滑动窗口的首项。
再循环 \(k\leftarrow 0\sim [\frac{W-j}{w[i]}]\),取 \(k\) 个物品 \(i\)。
接下来我们要求所有形如 \(dp[i][j+k\times w[i]]\) 的值。(以下滑动窗口)
若取了 \((k-t)\) 个物品 \(i\),答案是 \(dp[i-1][j+t\times w[i]]+(k-t)\times v[i]\)。
(实际上,只需要做到中括号里少一个 \(w[i]\),外面就多一个 \(v[i]\),就可以了)
因为我们最内层循环就是枚举 \(t\) 的,所有和 \(t\) 不相干的都相当于常数,可以分离,还剩 \(dp[i-1][j+t\times w[i]] - t\times v[i]\)。
我们需要求这种东西的最大值。
-
如果 \(k-q.front()>m[i]\),说明物品 \(i\) 取的个数太多了,即滑出窗口;
-
如果 \(dp[i-1][j+k\times w[i]]-k\times v[i]\geq dp[i-1][j+q.back()\times w[i]]-q.back\times v[i]\),队尾就被新来的完爆;
-
所有该弹的弹完之后,加入 \(k\);
-
现在的队头一定是最大的,用 \(q.front()\) 代入式子求即可。
-
-
我们已经求了 \(dp[1\sim n][0\sim W]\),因为我们的 dp 定义为“恰好”,所以我们需要循环 \(dp[n][0\sim W]\) 取最大。
-
复杂度 \(O(nW)\)。
【使用场景】
如果一个 dp 的转移方程可以变成:\(dp[i]=\max\{f(j)\}+g(i),h(i)\leq j\leq i\) 的形式,\(h(i)\) 是一个随着 i 增加而增加的函数,它就可以用单调队列优化。
注意:这里的 \(f(j)\) 指 “把 dp[i] 推出来的位置”,它不一定是体积、价值等题目中明确有变量表示的东西,因此,我们在做题时可能需要自己手动变形,把 \(f(j)\) 变形出来。
\(f(j)\) 仅关于 j 的原因:单调队列的作用实际上是替代掉了一重循环,所以如果 f(j) 在判断条件里面和 i 有关,那么在 i 变动的时候单调队列里面也会变,这样就太麻烦了(实际上更精确的说法,是不涉及任何更高层的循环变量)。
比如多重背包里面的三重循环,队列是开在第二层下的,并且是在第三层下面更新的。
实际上,如果判断条件里面多一个关于 \(j\) 的数(非参数),那么第二层每动一次,单调队列里每一个数都要变,于是单调性就不满足了,得重新排一遍。
【斜率优化】
斜率、截距等定义就不再赘述。
【引入】
假设我们有一张收入表,上面记录了几家公司在不同年份的收入。
不妨假设每家公司的收入都很稳定,这让它们的收入在表上呈直线,现在我们想研究某年哪家收入最高。
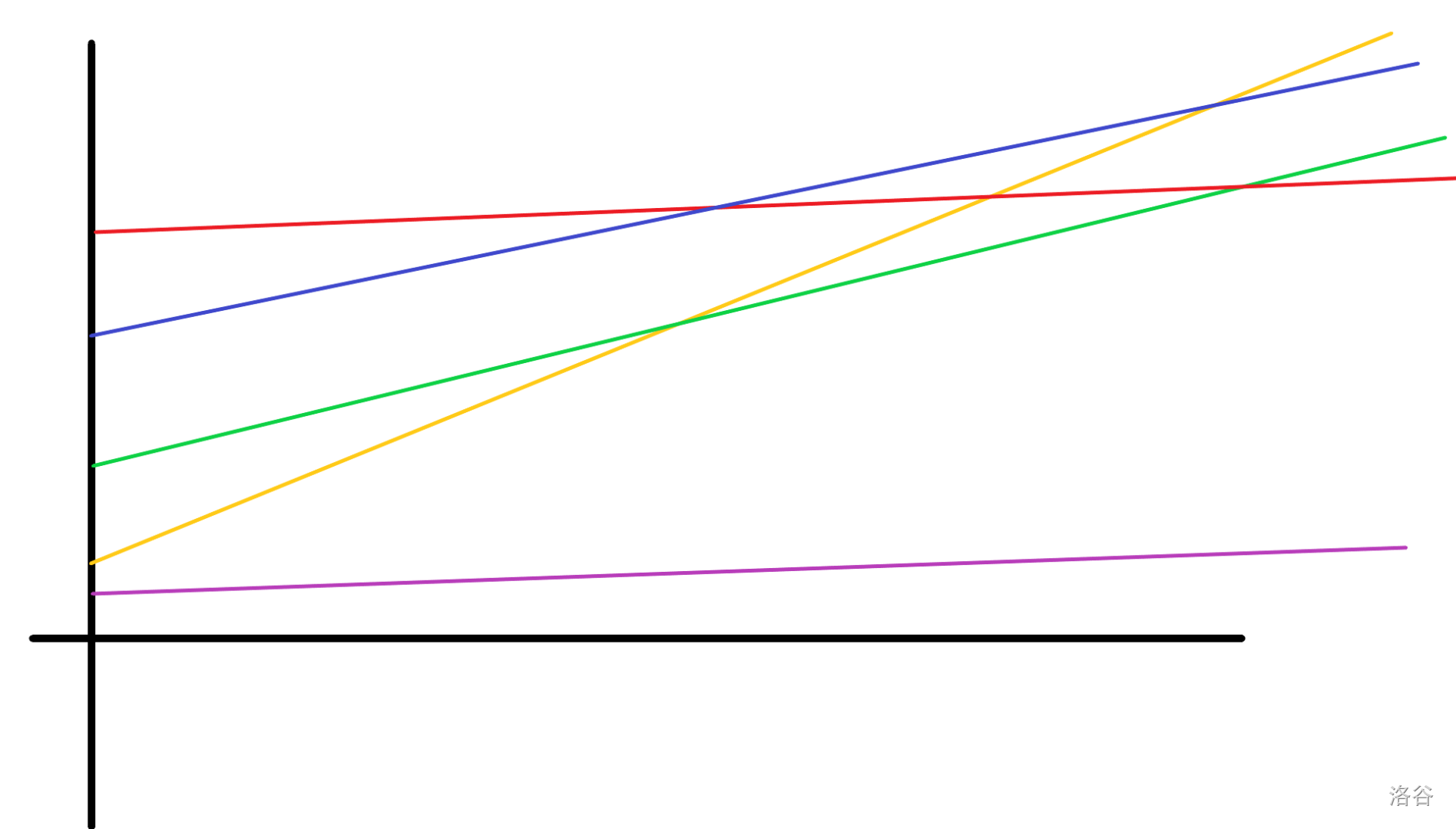
不如把横坐标看为时间,纵坐标看为收入。
我们发现,斜率在这里表示公司收入增长速度,纵截距表示公司初始资金。
显然,紫色公司一定不可能是答案,因为它被其他公司完爆了。
但是我们发现,绿色公司明明没有被任何公司完爆,它却始终无法出头。于是这家绿色公司就是多余状态,需要去除。
但是绿色公司为什么无法出头?我们发现,在绿色超越其他所有公司之前,先被黄色超越了,而被超越意味着以后黄色都比绿色强,于是绿色永无出头之日。
接下来我们研究一个更细的情况。(自动忽略完爆情况)
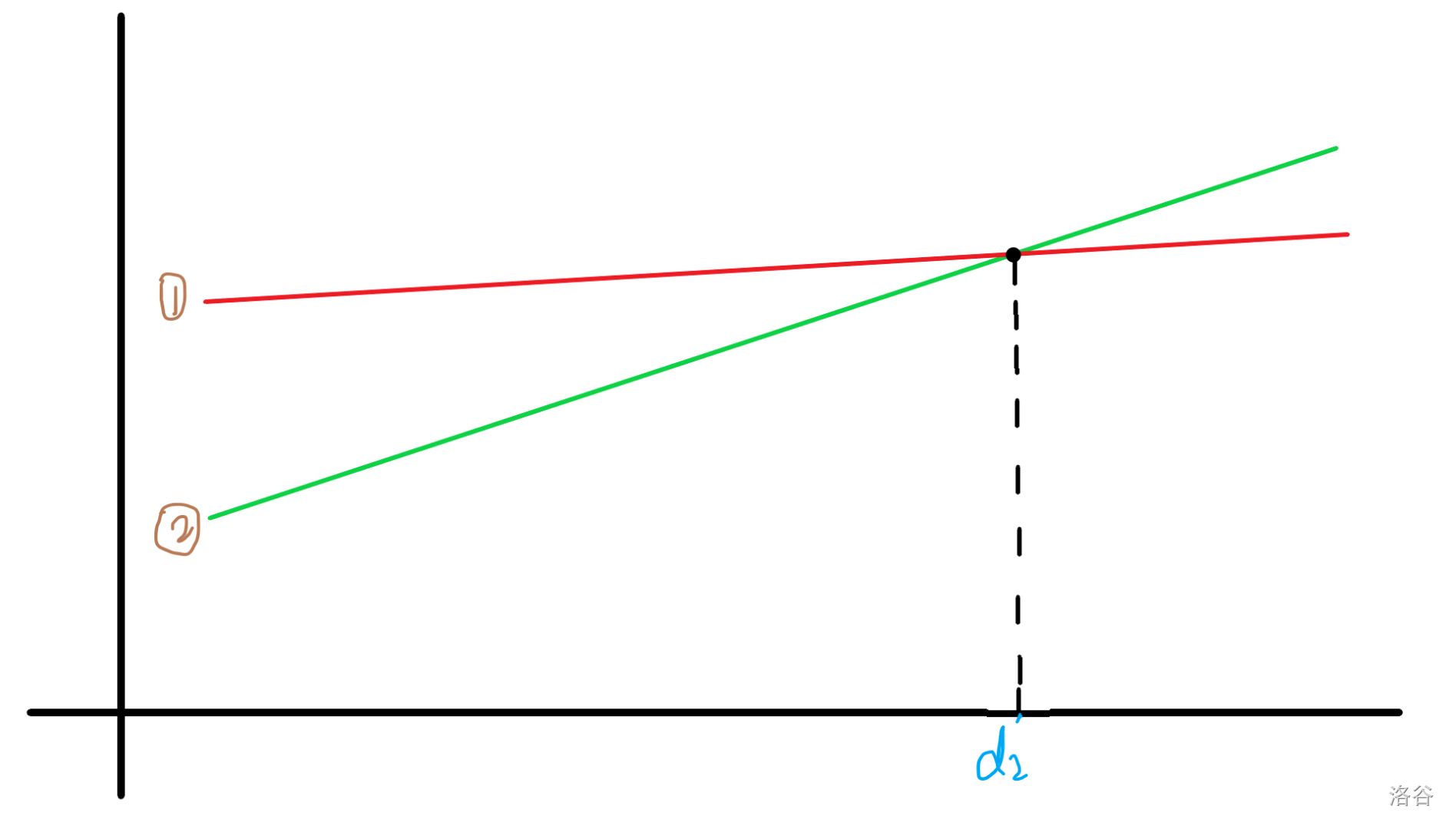
假设现在只有两条线,分别是 1、2 号。
我们定义 \(d_i\) 为:第 \(i\) 条线超过其他所有线的时间点,\(t_i\) 为:第 \(i\) 条线第一次被其他线超过的时间点(初始不算)。
显然,在这张图中 \(d_1=0,t_1=d_2,t_2=+\infty\)。现在再加入第三条线。
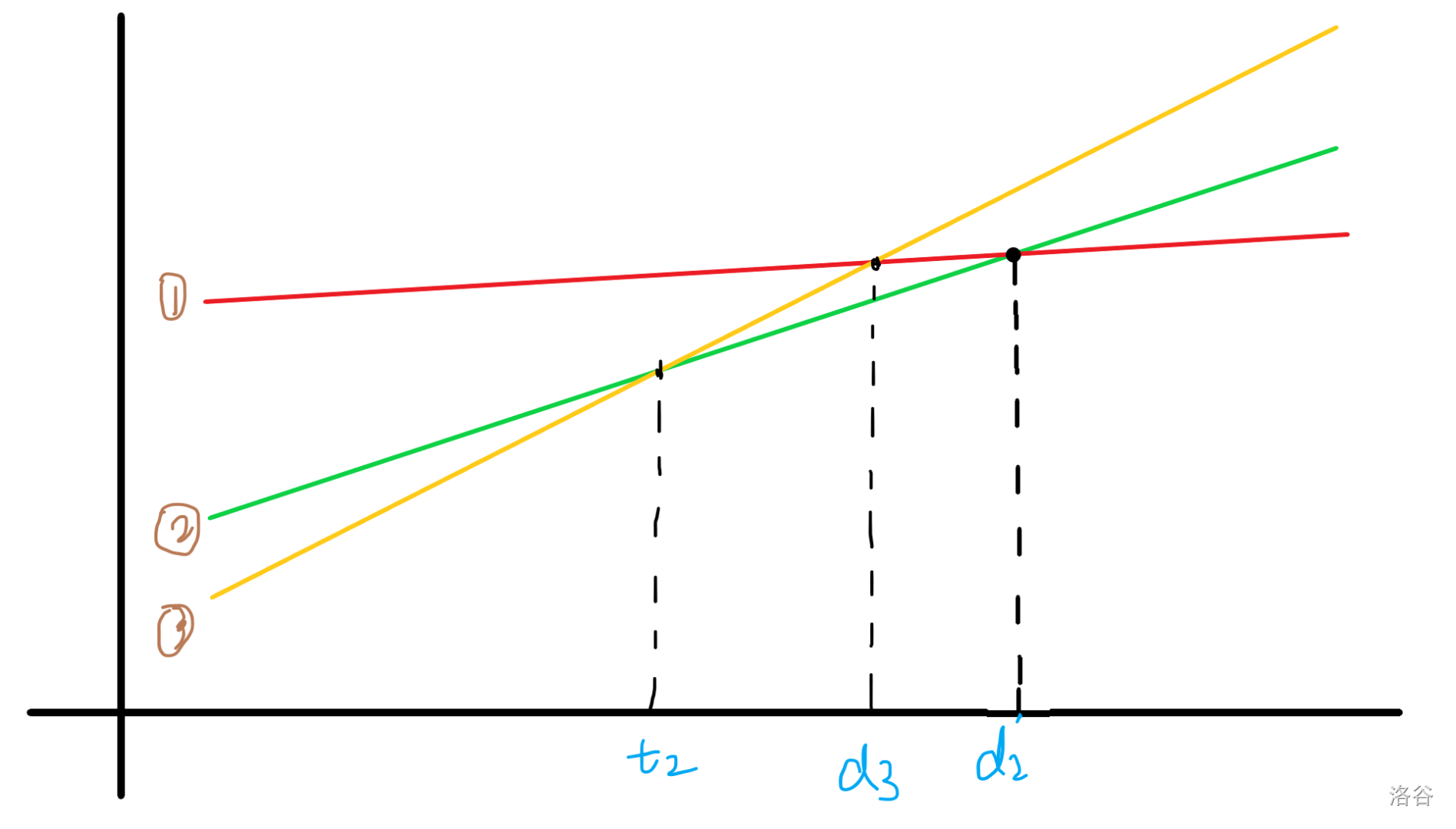
这个时候我们发现,这个时候 \(t_2\leq d_2\),这说明在绿色出头之前,他就被打下去了。
并且,因为黄色的斜率更大,绿色以后永远不可能比黄色大,所以在我们发现一条线在超越一切之前又先被超越了,那这条线段就不再有意义。这件事的条件是新来的线段斜率更大。
我们可以把这个说法变得更加具象化:如果一条线与 之前斜率最大的线 的交点 的横坐标 \(>\) 这条线与新线的交点的横坐标,那么这条线就没有存在的必要了。
这里进行详细解释:
-
为什么超越一切的地方就在 "与之前斜率最大的线的交点" ?
以红线超越一切的地方为例。
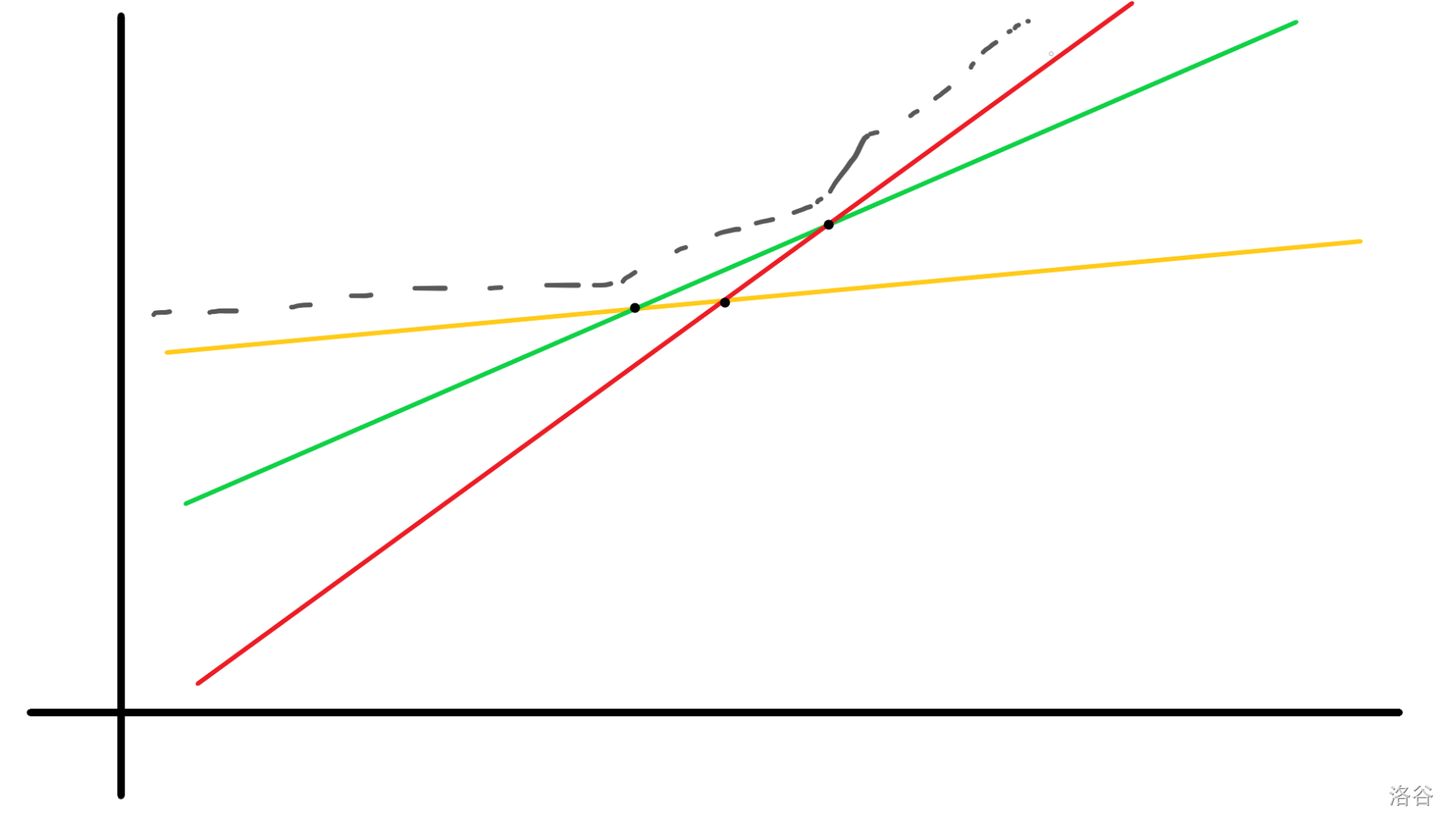
反证法,如果不在这里,说明在这个交点之上,还有另外斜率更小的线(黄线),是截距导致了这条线的交点更靠右。可是,因为黄线在这个交点之上,说明红线与黄线的交点一定比绿线与黄线的交点更靠左。
所以,绿线超越一切的地方,要比红线更晚,但是绿线却在更早之前被红线超越,那么按照我们的说法,绿线根本就不应该存在。矛盾。
所以命题得证,超越一切的地方就在 “与之前斜率最大的线的交点处”。这个命题的得证也证明了另一个命题:如果存在四条线 \(a,b,c,d,k_a\leq k_c,k_b\leq k_d\),那么 \(a,b\) 的交点一定比 \(c,d\) 的交点更靠左(不严格)。
-
我们发现了一个很神奇的单调性:随着时间增加,加入的线段的斜率也随之增加,所以新诞生的交点也往右走。
不要忘了我们的目的:求出某时刻最高的线段。
我们发现,这个东西用单调队列可以很好的处理:
一般用单调队列维护的东西只分四个步骤:
-
新加入的会把队尾元素弹出。实际上,不妨设当前队尾元素是 \(a\),队尾的倒数第二个元素是 \(b\),新加入的元素是 \(c\)。
如果 \(c\) 与 \(a\) 的交点比 \(b\) 与 \(a\) 的交点更靠左,那么 \(a\) 就可以弹出了。这是因为两点:我们的单调性说明队尾的后两个元素已经是斜率最大的元素了,而我们上面推出的结论可以知道,与 \(a\) 的超越时刻就是 与 \(b\) 的交点 了。而当 \(a\) 在超越一切之前先被别人超越了,\(a\) 就不再有价值。注意这里涉及了队尾的两个元素。
-
队头会因为过期出队。在这里,过期就代表在我们问的时刻时,队头的元素由于斜率太小,已经被后来的线超越了。这个时候因为队头的斜率小,之后不可能超回来,所以队头此时也可以弹掉。
-
加入新的线。
-
我们想要的答案是什么:队头就是我们想要的线。
-
经过这么分析,我们发现我们可以快速求出某一时刻最高点是哪条线了。
但是这个和 dp 有什么关系?
因为在我们的 dp 中,有时可以把问题变成类似于 “ 若干条直线,求某横坐标上的最高线段 ” 的问题。
【适用场景】
在上面的单调队列优化中,我们强调了一件事:\(f(j)\) 必须仅关于 \(j\),但是在这里,我们可以用斜率优化让这个条件变得宽松。
若我们可以把转移方程改成 \(dp[i]=\max\{k(j)\times x(i)+b(j)\}+t(i)\) 的形式,我们就可以考虑斜率优化。
在这里,\(k(j)\) 就相当于上面的斜率,\(b(j)\) 就相当于截距,\(x(i)\) 相当于查询的横坐标。
我们来综合考虑一下斜率优化需要满足什么条件。
-
转移方程改写为 \(dp[i]=\max\{k(j)\times x(i)+b(j)\}+t(i)\) 的形式,其中每个函数都是仅关于各自的变量。
-
如果是求 \(\max\),那么 \(k(j)\) 必须单调不减,这个条件相当于上面这件事的条件就是新加入的斜率更大。 如果是求 \(\min\) 就相反。如果不满足这个条件,那么加入线段就要加到中间去,效率降低(当然用优先队列和线段树也可以做)。
-
\(x(i)\) 随着 \(i\) 的增加单调不减,这个无关 \(\max\) 还是 \(\min\),因为这个的意义在于问问题的时刻是不减的,所以队头的元素不会出队又入队。
值得注意的是,我们虽然说是斜率优化,但是 \(x(i)\) 并不一定是一个关于 \(i\) 的一次函数:因为我们不在乎横坐标是什么,之间有什么关系,我们只需要不减。
另外,一开始我们设计出的转移方程可能并不满足斜率优化的形式,但是我们可以变形方程,让它符合条件。
【一些题目】
在这题里面,我们的物品没有体积,价值是 \(1\sim 6\),我们要做一个布尔型多重背包,并且第二维设为价值(当然把体积看为 \(1\sim 6\),第二维做体积也可以)。
因为是布尔型,所以我们并不关心大小,只关心真假,因此我们的只需要记下来最新的 true 即可。
我们可以用一个 pair 代替双端队列,记录当前窗口内是否有 true,和这个 true 的位置。如果循环中滑出窗口,就改为 false;如果碰到一个新的 true,就更新这个 pair。
在这题中,我们需要做两次背包。
对于 FJ:
我们的物品体积为 1,价值为 \(v\),且我们的多重背包第二维要做价值,然后求最小体积。(最少硬币数)
对于店主:
硬币数是无限的,这提醒我们要用完全背包。实际上,我们确实按照完全背包的方法求最小体积即可。
最后,因为 FJ 付的钱可能比 FJ 需要付的钱要多很多,所以我们最后求答案的时候需要枚举 \(T\sim M\!A\!X\!N\),其中 \(M\!A\!X\!N\) 表示 FJ 的硬币总和。(如果 dp 完毕,目标状态是 \(+\infty\),说明没法凑出这个金额)
注意点:初值是 \(+\infty\),需要滚动数组优化。
斜率优化,需要自己把转移方程变形。
定义:\(dp[i]\) 表示在 \(i\) 时刻发一次车,所有在 \(i\) 时刻之前的人的等待时间总和的最小值。
注意到因为在 \(i\) 时刻发车后,所有 \(i\) 时刻之前到的人一定都走了,因此这个状态定义有无后效性。
枚举上一次发车的时间点,注意到发车时间一定是一个人到达的时间,不妨设上一次发车时间为 \(j\)。
因为我们在第 \(i\) 时刻发车,所以在 \((i-m, i)\) 之间绝对不能发车,否则无法在 \(i\) 时刻回到人大附中,即 \(j\leq i-m\)。
有转移方程 \(dp[i]=\min\{dp[j]+\sum (i - t_k)\},j\leq i-m,t_k\in (j,i)\)。即 在 \(j\) 时刻发车的最小等待时间 + 在 \((j,i]\) 时刻到的人的等待时间总和。
\(\sum(i-t_k)=(cnt[i]-cnt[j])\times i - (sum[i]-sum[j])\)。
其中,\(cnt[x]\) 表示前 \(x\) 个时刻到的人数量,\(sum[x]\) 表示前 \(x\) 个时刻到的人的到达时刻之和。显然这两个东西可以预处理。
所以,\(dp[i]=\min\{dp[j]+(cnt[i]-cnt[j])\times i-(sum[i]-sum[j])\}\)
接下来,我们开始变形!
\(dp[i]=\min\{dp[j]+(cnt[i]-cnt[j])\times i-(sum[i]-sum[j])\}\)
\(dp[i]=\min\{dp[j]+cnt[i]\times i-cnt[j]\times i-sum[i]+sum[j]\}\)
\(dp[i]=\min\{-cnt[j]\times i + (dp[j]+sum[j])\} + cnt[i]\times i-sum[i]\)
我们发现现在的转移方程很标准:\(k(j)=-cnt[j],x(i)=i,b(j)=dp[j]+sum[j],t(i)=cnt[i]\times i-sum[i]\)。
于是我们现在就可以进行斜率优化了。
注意,\(j\) 可以用来更新的首要条件是 \(j\leq i-m\)。
整理一下:
-
因为我们可能在最后一个人到来前一秒开车,所以我们的 dp 范围应当是 \([1,mx+m)\);
-
在 dp 过程中,只有 \(i-m>0\) 时才考虑往队列中加入新元素(\(i-m\));
-
斜率优化单调队列四步:(左闭右开写法)
-
弹队尾。新加入的元素是 \(i-m\),我们设直线 \(l_1:y=k(q[r-2])\times x+b(q[r-2])\),\(l_2:y=k(q[r-1])\times x+b(q[r-2])\),\(l_3:y=k(i-m)\times x+b(i-m)\)。(注意,必有 \(k_{l_1}>k_{l_2}>k_{l_3}\))
按照我们上面的结论,如果 \(l_1,l_2\) 交点的横坐标 \(>\) \(l_2,l_3\) 交点的横坐标,那 \(l_2\) 永无出 (低) 头之日。
所以我们写一个函数 \(cal(i,j)\) 表示 \(y=k(i)x+b(i),y=k(j)x+b(j)\) 的交点的横坐标。
若 \(cal(q[r-2],q[r-1])>cal(q[r-1],i-m)\),则可弹出队尾;
-
加入新元素。我们就加入 \(i-m\),即可能会用来更新的状态;
-
弹队头。如果 \(cal(q[l],q[l+1])\) 的交点横坐标 \(<x(i)\),就弹队头(队头可能是最低的时间段过去了);
-
求答案。此时的队头就是所有可以用来更新的状态中,最小的那一个。
-
-
最终答案:循环 \(dp[mx]\sim dp[mx+m-1]\) 求最小,\(mx\) 为到达时间最晚的那个。
注意:特判 \(cal()\) 中两条线斜率相等的情况,因为 \(k()\) 非严格递增。
注意:这题刚好 \(b()\) 也满足单调递增,否则我们需要写一个判断队尾被完爆的判断。(截距大,斜率也大)
斜率优化。调了 1 week。
考虑 dp: \(dp[i]\) 表示将第二个锯木厂建在第 \(i\) 棵树的最小代价(显然锯木厂建在树的位置最好)。
那么枚举第一个锯木厂的位置 \(j\): \(dp[i]=\min\{sum - w[j] \times d[j] - (w[i] - w[j]) \times d[i]\} (1 \leq j < i)\),其中 \(w[j]\) 为 \(1\sim j\) 的重量之和,\(d[j]\) 为 \(j\) 到山脚的距离,\(sum\) 为所有树去山脚的代价。(按照 总代价 - 第一个锯木厂节省的 - 第二个锯木厂节省的)
开始变形。
\(dp[i]=\min\{sum - w[j] \times d[j] - (w[i] - w[j]) \times d[i]\}\)
\(dp[i]=\min\{sum - w[j] \times d[j] - w[i]\times d[i] + w[j]\times d[i]\}\)
\(dp[i]=\min\{w[j]\times d[i]-w[j]\times d[j]\}+sum-w[i]\times d[i]\)
这已经是一个 \(dp[i]=K(j)X(i)+B(j)+T(i)\) 的形式了,但是发现一个问题:\(K(j)\) 递增,\(X(i)\) 递减,于是我们把 \(K(),X()\) 同时取相反数。
\(dp[i]=\min\{(-w[j])\times (-d[i])-w[j]\times d[j]\}+sum-w[i]\times d[i]\)
此时令 \(K(j)=-w[j],X(i)=-d[i],B(j)=-w[j]\times d[j],T(i)=sum-w[i]\times d[i]\),就是斜率优化的模板。
接下来有若干个注意点:
-
求 \(sum\) 的时候,一定要先求 \(d\) 的前缀(每棵树到山脚的距离),然后立刻循环求 \(sum\),不要把 \(w\) 也搞了前缀和再循环求;
-
因为可能几棵树堆在一起,\(K()\) 可能相等,要加特判;
-
因为 \(i\) 是第二个锯木厂的选址,所以从 2 开始枚举,同时因此我们的单调队列里面一开始就要存一个 \(1\) 作为更新的初始状态(当然,如果就是要从 1 开始循环也不是不行);
-
因为枚举状态是 \(j<i\),严格小于,所以要在加入元素 \(i\) 对应的元素之前就更新 \(dp[i]\);
-
如果判断队头过时的 while 放在 dp 更新之前,应该是 \(X(i)\),如果在更新之后,应该是 \(X(i+1)\);
-
在判断队头过时的时候,判断条件应该是 \(X(i+1)\) 而非 \(i+1\) !!!!