树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链。
——百度百科

重链剖分

概念 1 重儿子

一个父节点的所有儿子中，子树节点最大（siz 最大）的节点。

记为 son[u]=v。

概念2 轻儿子

父节点所有儿子中，除过重儿子的所有节点。

概念3 重边

由父亲节点和重儿子连接成的边。

概念4 轻边

由父亲节点和轻儿子连接成的边。

概念5 重链

由多条重边连成的链。

概念5 轻边

由多条轻边连成的链。

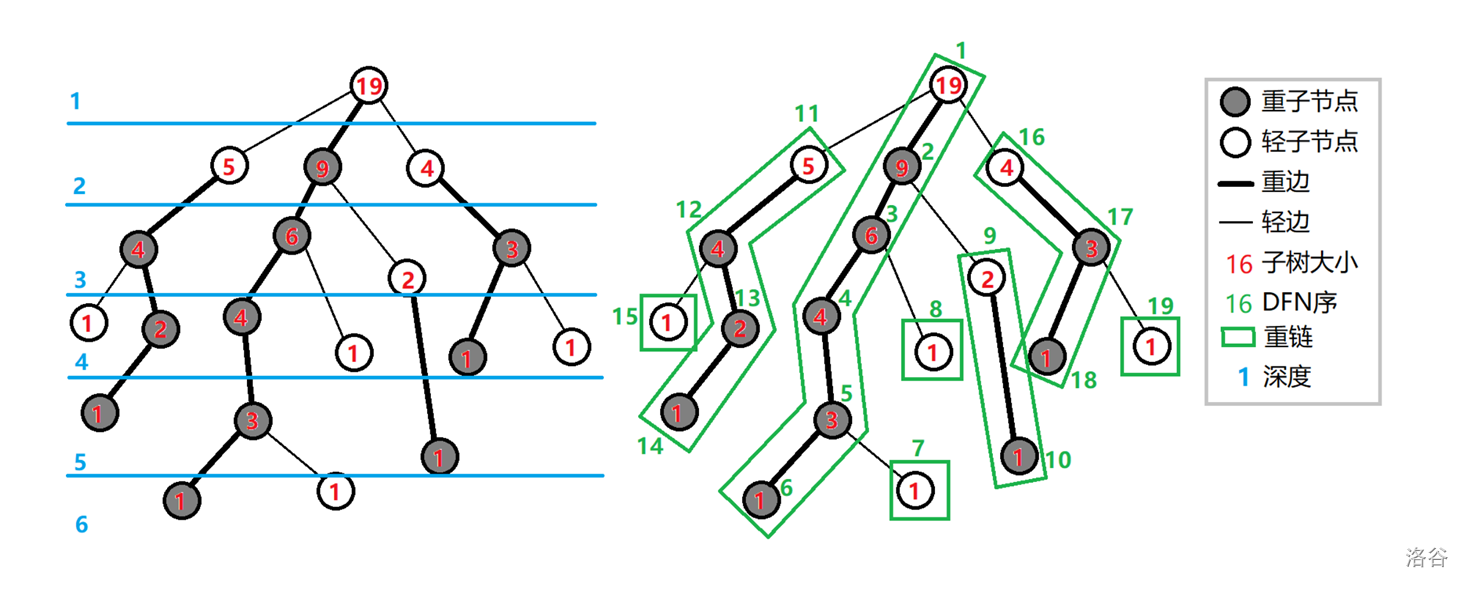
实现思路

1. 对于一个节点先找出它所在的子树大小，同时我们可以得到它的所有子节点的子树大小 siz[v]，这样我们可以得到此节点的重儿子。

例如，点 1 的三个儿子分别是 2,3,4。
2 所在的子树大小为 5，
3 所在的子树大小为 2，
4 所在的子树大小为 6，
那么 1 的重儿子就是 4。

2. 在 dfs 的过程中顺便记录节点 u 的父亲 f[u]，从根节点的深度 dep[u]等。

3. 再来一遍 dfs，连接重链，标记每个节点的 dfs 序，处理出每个节点所在重链的顶点 top[u]和节点编号 id[u]。

代码实现

第一遍 dfs

作用主要是找出每个节点的深度和重儿子。

int son[500010],deep[500101],f[500101];
int siz[500010];
//son：重儿子
//deep：节点深度
//f:节点的父节点 
void dfs1(int u,int fa)
{
	f[u]=fa;
	deep[u]=deep[fa]+1;
	siz[u]=1;
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[son[u]]<siz[v])
		son[u]=v;
	}
}

第二遍 dfs

作用主要是求出每条重链的顶点和节点的 dfs 序。

//rk：节点编号 
//id：dfn序
//top:重链顶端 
void dfs2(int u,int t)
{

	top[u]=t;
	if(son[u])dfs2(son[u],t);
	id[u]=++cnt;
	rk[cnt]=u;
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==son[u]||v==f[u])continue;
		dfs2(v,v);
	}
}

这样就完成了树链剖分的基础操作（链式前向星存图）。