底和项
讨论底(floor,最大整数)函数和项(ceiling,最小整数)函数,对于所有实数 \(x\),其定义如下:
\(\lfloor x \rfloor=\) 小于或等于 x 的最大整数;
\(\lceil x \rceil=\) 大于或等于 x 的最小整数。
接下来我们来了解底函数和项函数的图形,其在直线 \(f(x)=x\) 的上方和下方形成阶梯状的模式。
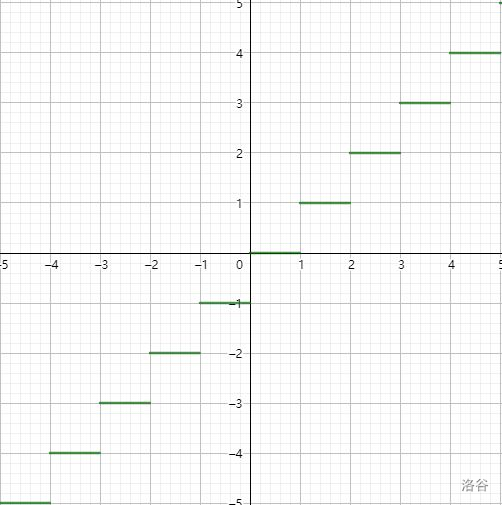
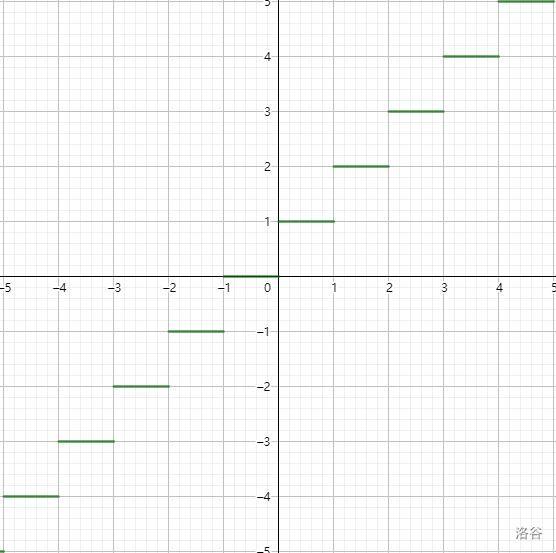
观察图形,底函数位于直线 \(f(x)=x\) 上或其下方,有 \(\lfloor x \rfloor≤x\);类似地,有 \(\lceil x \rceil≥x\),当然,这两函数在整数点的值相等:
\(\lfloor x \rfloor=x⇔x\) 是整数 \(⇔\lceil x \rceil=x\)。(用记号 \(⇔\) 表示“当且仅当”)
此外,当它们不相等时,项函数恰好比底函数大 \(1\):
\(\lceil x \rceil-\lfloor x \rfloor=[x\) 不是整数 \(]\)。
如果将对角线向下平移一个单位,它就完全在底函数下方,就有 \(x-1<\lfloor x \rfloor\);类似地,有 \(x+1>\lceil x \rceil\),组合起来有:
\(x-1<\lfloor x \rfloor<x<\lceil x \rceil<x+1\)。
最后,这些函数关于两个坐标轴互为反射:
\(\lfloor -x \rfloor=-\lceil x \rceil;\lceil -x \rceil=-\lfloor x \rfloor\)。
下面给出四条法则来说明这些事实:(\(x\) 为实数,\(n\) 为整数)
\(\lfloor x \rfloor=n⇔n≤x<n+1\);
\(\lfloor x \rfloor=n⇔x-1<n≤x\);
\(\lceil x \rceil=n⇔n-1<x≤n\);
\(\lceil x \rceil=n⇔x≤n<x+1\)。
有可能将一个整数移进或移出底或者项:
\(\lfloor x+n \rfloor=\lfloor x \rfloor+n\)。
但是一般不能将一个常数因子移出去:\(\lfloor nx \rfloor≠n\lfloor x \rfloor\)。
再给一些显然的法则:
\(x<n⇔\lfloor x \rfloor<n\);
\(n<x⇔n<\lceil x \rceil\);
\(x≤n⇔\lceil x \rceil≤n\);
\(n≤x⇔n≤\lfloor x \rfloor\)。
\(x\) 和 \(\lfloor x \rfloor\) 之间的差称为 \(x\) 的分数部分(fractional part)。其记号:
\(\{x\}=x-\lfloor x \rfloor\)。
可以称 \(\lfloor x \rfloor\) 是 \(x\) 的整数部分。
下面推导一下 \(\lfloor x+y \rfloor\),记 \(x=\lfloor x \rfloor+\{x\}\) 和 \(y=\lfloor y \rfloor+\{y\}\),那么就有 \(\lfloor x+y \rfloor=\lfloor x \rfloor+\lfloor y \rfloor+\lfloor \{x\}+\{y\} \rfloor\),又因为 \(0≤\{x\}+\{y\}<2\),那么会发现 \(\lfloor x+y \rfloor\) 要么等于 \(\lfloor x \rfloor+\lfloor y \rfloor\);要么等于 \(\lfloor x \rfloor+\lfloor y \rfloor+1\)。
标签:,lfloor,lceil,函数,整数,rfloor,rceil From: https://www.cnblogs.com/Exotic-sum/p/18010769