标签：结点 int sum 查集合并 fnd

【并查集是什么】

并查集是用来表示一些不相交集合的算法。

它可以很快地处理两个点之间是否在一个连通块中。

【并查集的特点】

动态合并集合；
合并之后就不能拆开了。

并查集开始前，先按顺序把初始集合编号。

（初始也不一定每个都是单个元素）

【并查集的实现】

数据结构分类：抽象结构、存储结构。

抽象结构：画出来的形式（就像一棵树画在纸上，有结点也有边）；
存储结构：实现代码的形式（vector数组）。

并查集的抽象结构：一些集合。

存储结构：树。

把并查集比作一些小组，小组之间会合并。

初始集合 1~n 编号。

\(p_i = x\) 表示：\(i\) 的上级是 \(x\)。

初始：\(p_i = i\)。（每个人自成一组）

并（unn）：每次合并 \(x\)、\(y\)，令 \(p_x = y\)。

合并时，把 \(x\) 和 \(y\) 所在组合并，\(x\)、\(y\) 未必就是组长。

并查集的存储结构很像森林。

如果把 \(i\) 连向 \(p_i\)，差不多就是森林。

所以，\(p_i\) 可以近似看作 \(i\) 的父结点。

森林中，一棵树的根结点（组长）有一个自环。（初始化）

查（fnd）：只要两个元素所在组的组长相同，这两个元素必定在同一组（不可能重复）。

如果一个元素的 \(p\) 就是自己，这个元素就是组长。

（这个元素没有其他父结点）

并，需要通过查来实现：

合并 \(x\) 和 \(y\) 的组，只把 \(x\) 的组长的父结点变成 \(y\) 的组长（如果 \(x\) 和 \(y\) 同组就啥也不干）。

查 \(y\) 组的时候，不会影响，因为不会跑到 \(x\) 去。

查 \(x\) 组的时候，到了原本的根结点也不会停，因为此时的原根结点的父结点不是自己，而是 \(y\) 的组长，于是会返回 \(y\) 组长。

合并两个组，只和两个组的组长有关系，和其他任何无关。


void init() {
    for (int i = 1; i <= n; i++)
        p[i] = i;
}

int fnd(int x) {
    if (p[x] == x)
        return x;
    return fnd(x);
}

void unn(int x, int y) {
    int xx = fnd(x), yy = fnd(y);
    if (xx == yy)
        return ;
    p[xx] = yy;
}

【优化：路径压缩与按秩合并】

注：仅一个优化可能是不够的。

两个优化板子题

【按秩合并：小树连大树】

这里有两棵树，我们要合并它们。

那我们是把规模小的连向规模大的，还是大的连向小的？

是小的连大的，这个优化可以把查询复杂度优化到 \(\log\) 级别。

证明：查询时每往上走一个，当前子树规模至少乘二。

如果是大连小，就有可能构造出一条链，就变成 \(O(size)\) 了。

void unn(int x, int y) {
    int xx = fnd(x), yy = fnd(y);
    if (xx == yy)
        return ;
    if (sz[xx] > sz[yy])
        swap(xx, yy);
    p[xx] = yy;
    sz[yy] += sz[xx];
}

【路径压缩：缩小深度】

因为我们的fnd是一步一步往上走的，而且我们只关心根结点是谁。

所以，我们希望每个点距离根结点都要更近一些。

如果一个结点距离根结点很远，其实我们可以把它的父结点直接改成根，这样不影响查询结果。

而且，我们进行每一次查询时，因为是不断往上递归的。

所以，这条递归上去的路径上的所有点，我们回溯时都可以把它的父结点改成根结点。

等我们下次再查询的时候，只要往上走一步，就直接到根结点了。

int fnd(int x) {
    if (p[x] == x)
        return x;
    return p[x] = fnd(p[x]);
}

【类似树上前缀和的并查集】

Experience

还是需要两个优化。

这里的难点：两个组合并之后，它们的经验依然可能不同。

考虑一个类似树上前缀和的手法：

加经验值，只在根结点上加。

一个点的经验值，就是从它到根结点路径上所有点上的经验值的和。

但是，我们合并的时候，在这之前两个集合的经验是不能共享的，我们这么合并却都算了进去。

所以，我们在合上去的那棵树的根结点，减去另一个根结点上的经验。（类似于补偿回来）

举个栗子：我们合并这两颗树。

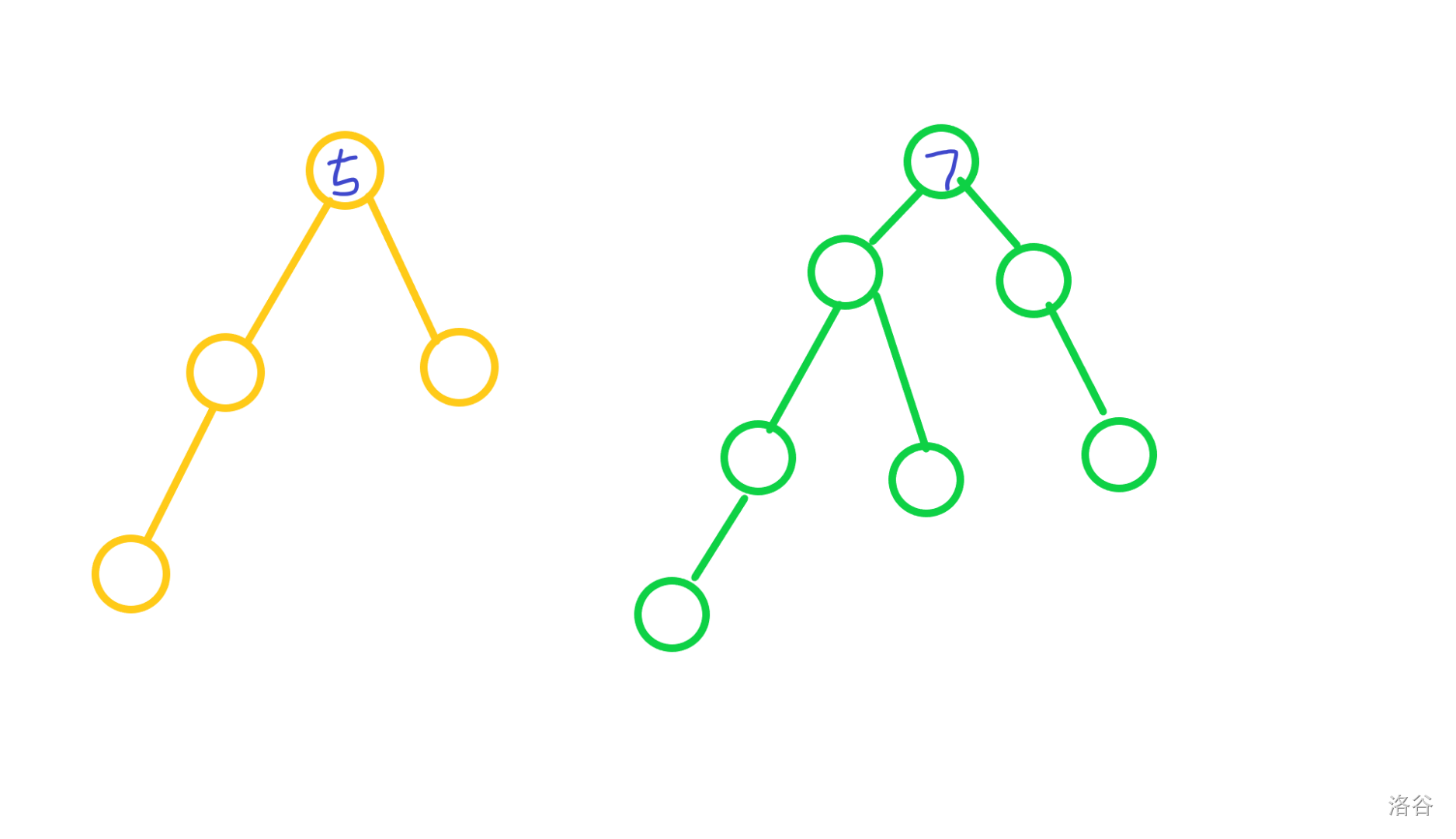
合完变成这样：

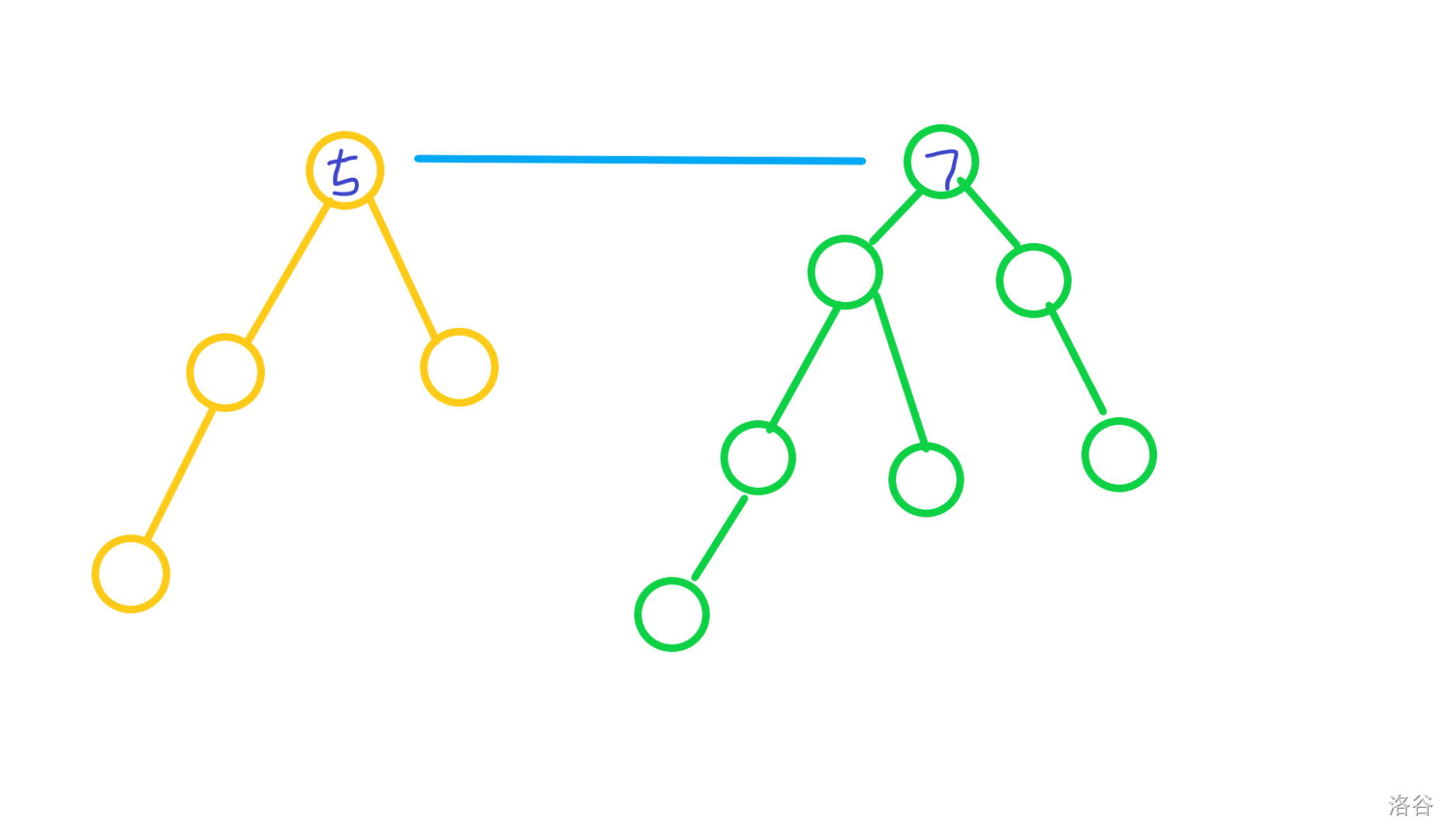
但是左边黄树的点本来应该是 5 经验，合并之后都变成 12 经验了。

于是我们补偿。

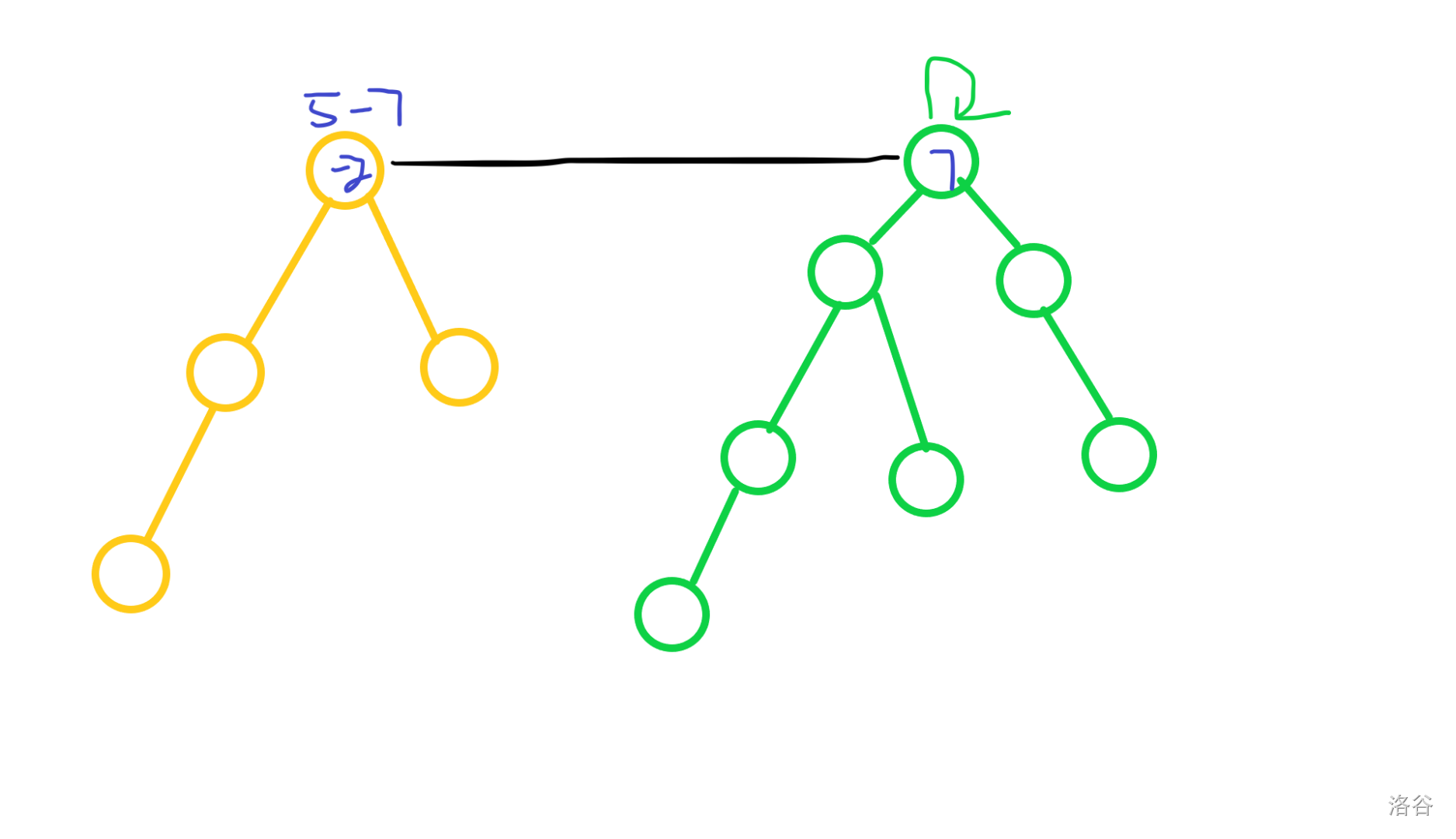
这样左边的经验值就对了。

以后再给这组加经验，就直接在新根结点加即可。

（因为从黄到绿根，一定恰好经过黄根一遍，我们在黄根减掉即可）

【怎么进行两个优化】

首先按秩合并一定可以，因为我们都没有关心谁连谁的问题。

但是，路径压缩怎么进行？

我们定义 \(sum_x\) 为 \(x\) 的经验值。

如果不进行路径压缩，\(sum_x\) 就要不停通过 \(p_x\) 递归，每递归一次就把递归到的结点的经验值加到 \(sum_x\) 上，这显然是可行的。

但是，我们发现：一个点的 \(sum\)，等于它到根结点路径上的所有点的经验值之和。

我们进行一个这样的操作：递归的时候顺手把上面的经验加到相邻的下面

（如果上面的就是根结点就不加了，因为下面输出的时候会加）。

输出的时候输出这个点的经验加根结点的经验（如果本身就是根结点就不加了）。

例子：

假设我们要算最下面的点的经验。

当他递归到根的时候，返回；

退到了经验 2 的点，因为上面是根结点，所以直接返回；

退到了经验 3 的点，上面不是跟结点，加：

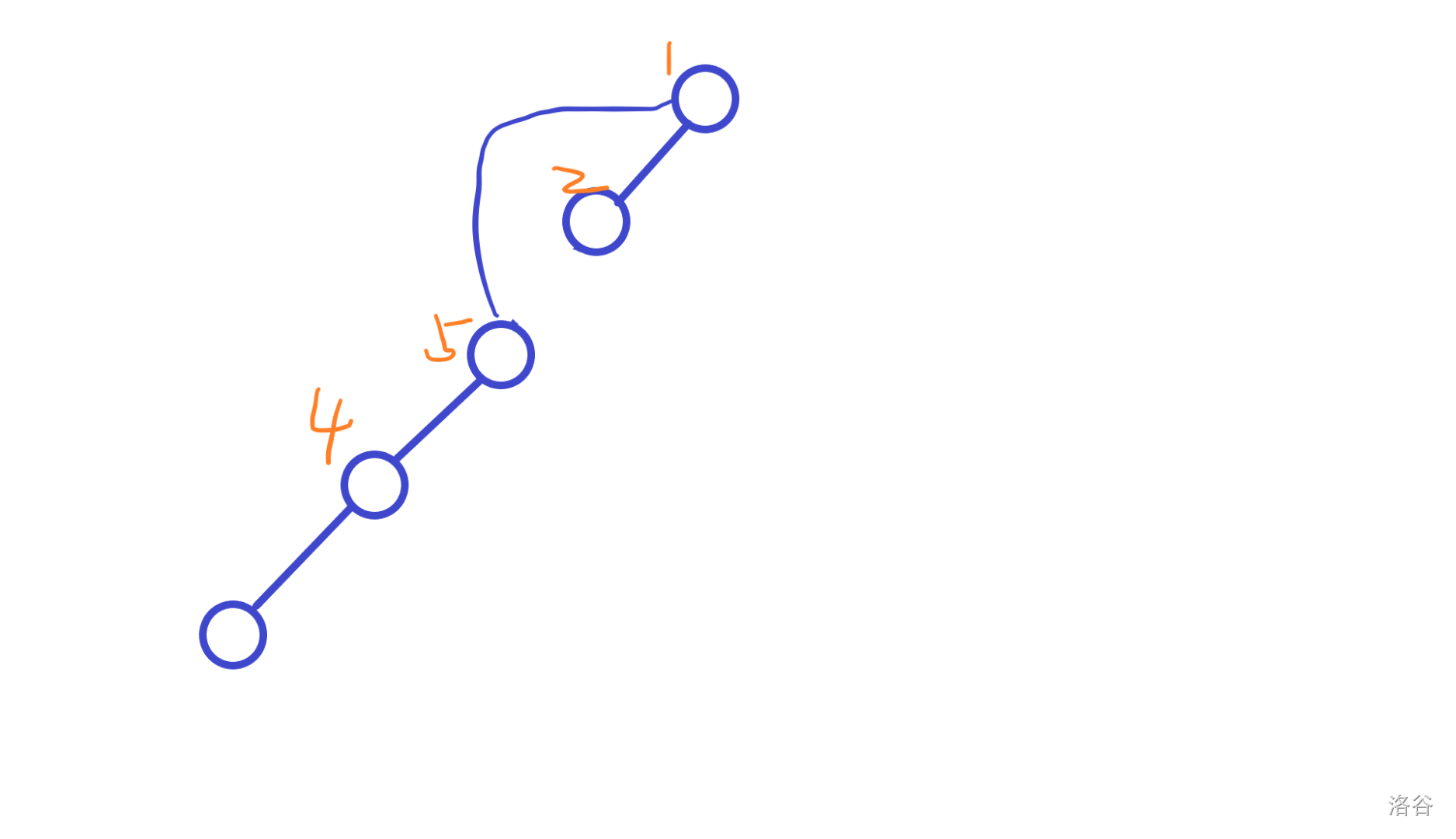
再退，退到经验 4 的点，加：

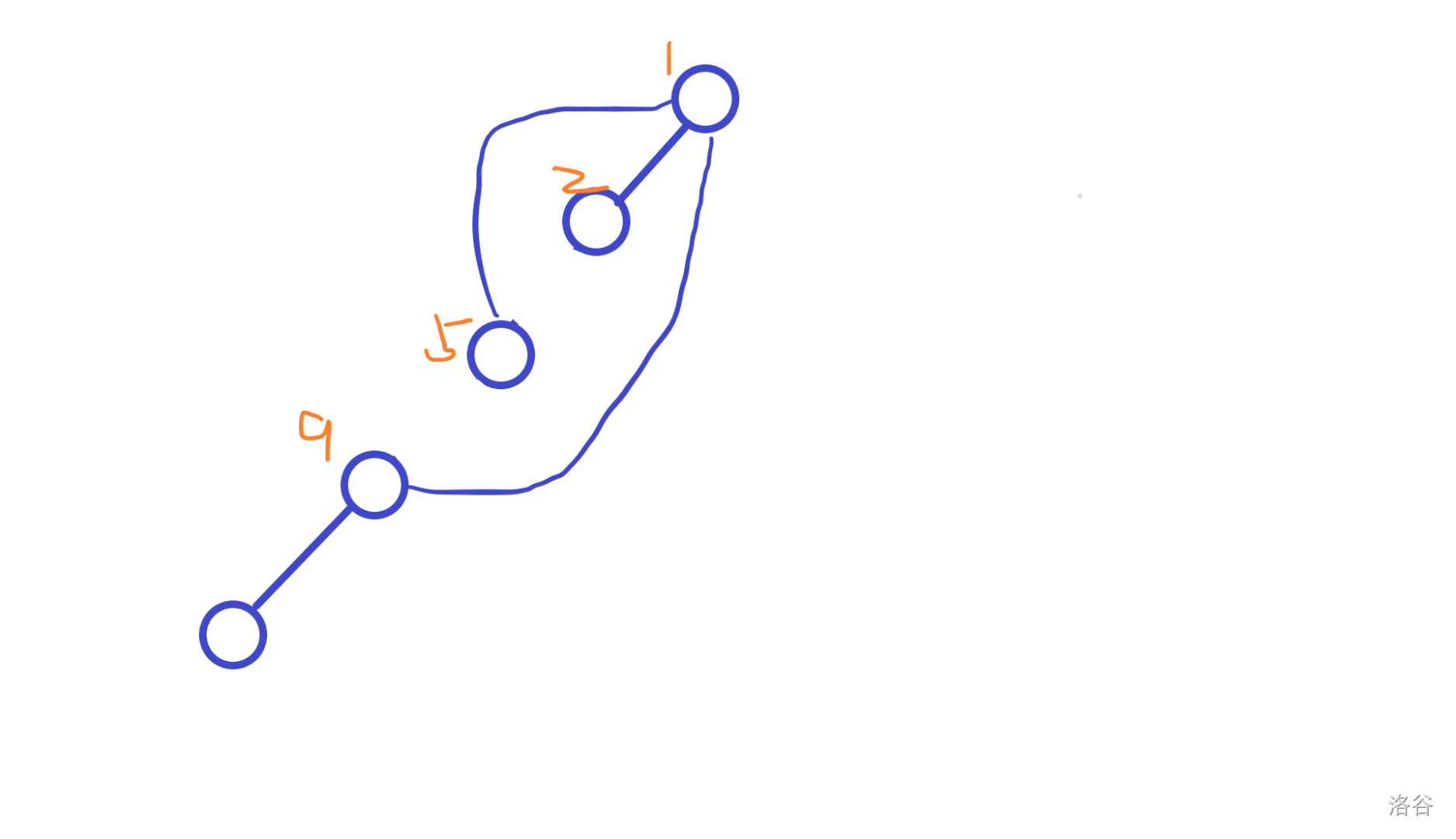
注意，加的不是3，而是5 。

我们可以发现，这相当于把从父结点到根结点的儿子都加了。

（类似前缀和递推）

于是我们最下面的点经验值变成 9。

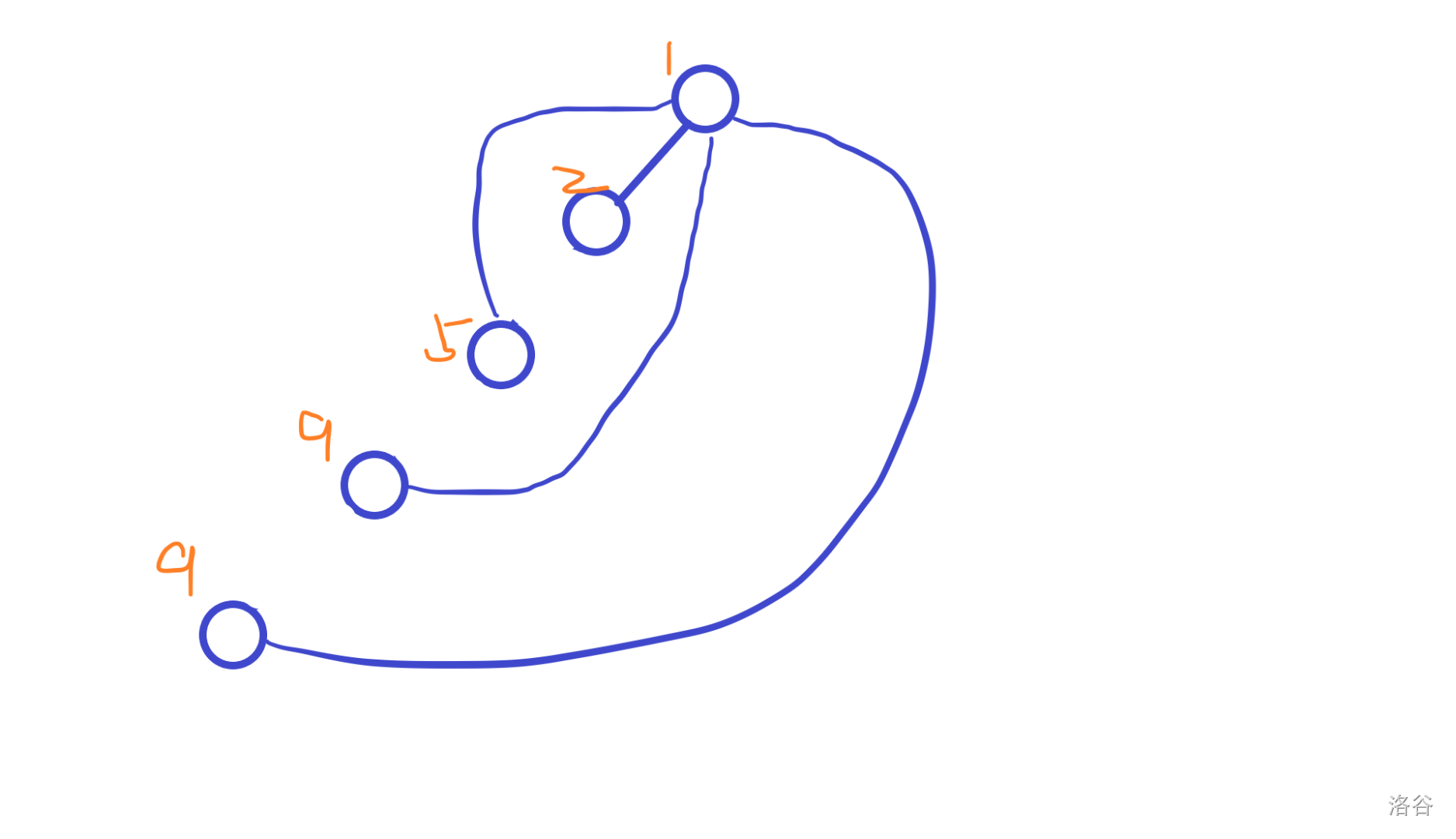
而此时我们查询这个路径上任何一个点，按照上面输出的规则，都是正确的。

#include <bits/stdc++.h>
using namespace std;

int n, m, x, y, v;
string s; 
//p[i]表示i与谁在一组,sz[i]表示i代表的组的集合个数
//sum[i]为i的标记，i到跟的路径标记之和为i的经验值 
int p[200005], sz[200005], sum[200005]; 
void init() {
	for (int i = 1; i <= n; i++)
		p[i] = i, sz[i] = 1, sum[i] = 0;
} 
int fnd(int x) {//返回x所在组的代表 
	if (p[x] == x)
		return x;
	int rt = fnd(p[x]);//先记录根是谁
	//这说明此次是有效路径压缩 ，且因为已经递归压缩了p[x]，故此时只压缩了p[x]这个点
	if (p[x] != rt) 
		sum[x] += sum[p[x]]; 
	return p[x] = rt; //路径压缩，每个点直连根节点 
}
void unn(int x, int y) {//合并x,y所在组
	int rx = fnd(x), ry = fnd(y);//x,y所在组代表 
	if (rx == ry) //是同一组 
		return ;
	if (sz[rx] > sz[ry])//确保小连大 
		swap(rx, ry);
	//rx一方的点，在rx多减一次sum[ry],在ry多加一次 sum[ry]，值仍然正确；ry一边则不受影响 
	sz[ry] += sz[rx], sum[rx] -= sum[ry];
	p[rx] = ry;//rx合并进了ry组 
}
int main()
{
	cin >> n >> m; 
	init();
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == "join") {
			cin >> x >> y;
			unn(x, y);
		}
		else if (s == "add") {
			cin >> x >> v;
			sum[fnd(x)] += v;//直接加到根，因为本组所有路径恰好算根一次 
		}
		else {
			cin >> x;
			if (fnd(x) == x) //根到根的路径只有自己 
				cout << sum[x] << endl; 
			else
				cout << sum[x] + sum[fnd(x)] << endl;
		}
	}
    return 0;
}

【带权并查集】

类似于上面的 \(sum\)，这里的权应该是一个合并的时候顺手就维护了的属性。（不用写边结构体）

银河英雄传说

这题里面带的权就是到根结点（头部飞船）的距离。

注意：这里还是只有根结点会带权，其他点在合并的时候千万别动！！！

求两个点之间的距离，就是两个点到头部飞船的距离之差。

Parity Game

定义点：一次回答（l 和 r）。

这题的权就是奇偶性（01）.

两个点在一个集合，只当它们存在一个共同端点，或者可以通过若干个其他有共同端点的点到达。

两个点之间的距离就是它们之间有奇数个还是偶数个1。

（因为a+b和a-b同奇偶，所以求距离只要到根的距离相加即可，不用考虑同侧）

如果在一个集合里面有矛盾的（和是0，却有一个是1），就有问题。

【改造问题】

【离线倒序】

Closing the Farm

这题是不断删边，但是并查集只能处理合并的关系。

考虑把所有操作存下来，再倒过来，就变成不断加边了。

如果有加有删，就另想他法吧（可持久化？）。

【类拆点】

团伙

定义点是一个人。

朋友的关系是传递的，但是敌人的关系却不是。

考虑对每一个点 \(i\)，\(i+n\) 是他的 “敌人窝点”。

他的每一个敌人，和他的敌人窝点成为朋友。

这样就把敌人关系也改成传递的了。

答案：

一开始 ans 是 n。

只要是朋友关系合并了，ans 就减一（不是敌人窝点的朋友）。

如果是敌人窝点，优先让实际的人作为根

食物链

每个点拆成三个：同类，吃它的，被它吃的

【洛谷题单：并查集基础】

并查集模板模板，没什么好说的。
村村通顺手统计一下集合个数。
家谱不知道为啥用 getchar() 莫名其妙T了几回。
Milk Vists S WA了一次，因为忘记特判两个点在一起。
Closing the Farm 离线倒序。
MooTube 一开始没想出来倒序（完全倒过来）有啥用，但是后来想到离线可以随便排序，然后降序一排就A了。（边写成升序了卡了三分钟）
团伙拆成俩。
食物链一开始没有想好拆出来的三种点之间的关系。
Parity Game 离散化写错一下。
银河英雄传说

int fnd(int x) {
    if (p[x] == x)
        return x;
    p[x] = fnd(p[x]);
    dis[x] = dis[p[x]] + 1;
    return p[x];
}

这段代码有两个错误。

第一个：

定义的 \(dis_x\)：x到根结点的距离，是可能 “跳跃”的

所以，不能写+1，因为你根本 \(p_x\) 和父结点不是一回事。

第二个：

在更新 \(dis\) 之前，\(p_x\) 已经被更新过了，导致 \(dis\) 一直加的是现在根结点的距离。（也就是不会变）

所以，用旧 \(p_x\) 更新 \(dis\)，就不能先更新 \(p_x\) 。

正确写法：

int fnd(int x) {
    if (p[x] == x)
          return x;
    int fa = fnd(p[x]);
    dis[x] += dis[p[x]];
    return p[x] = fa;
}

【CF 的 EDU】

step1

Disjoint Sets Union 按秩合并+路径压缩板子。
Disjoint Sets Union2 额外记录 sz, mx, mn。
Experience 经典路径压缩时记录属性，类似前缀和。
Cutting a graph 离线倒序。

step2

People are leaving 注意不能按秩合并，而且这题卡输入输出！！！
Parking 上一题的环形版
Restructuring Company 加一个nxt数组，但是这题居然也卡输入！！！
Bosses 普普通通。
Bipartite Graph 小小的拆点。
First Non-Bipartite Edge 和 I 大同小异，一开始没看到是二分图就要输出 -1 挂了一次。

【选做题】

修复公路板子。

扩散注意要除以二。

星球大战开了一堆数组记录有没有被炸掉，改了 5 分钟。

Monkeys 有意思！

首先，并查集不能处理分开（掉下来），所以离线倒序。

其次，考虑带权并查集，类似 Experience 的方式。

\(d_i\) 是猴子 \(i\) 掉落的时间，路径压缩的时候顺便更新。

让 1 号猴子作为永远的根结点。

（这也说明不能按秩合并）

每只猴子的掉落时间，就是从它到根结点的和。

每次合并时，如果哪边有 1，另一边的根结点的 \(t\) 就更新为当前时间。

因为 1 是永远的根结点，所以 1 上边不会有其他点，所以不会有时间会被重复计算。

最后还有一个小细节，一定要先压缩一遍路径才输出，因为路径压缩相当于更新一遍。

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 2e5 + 5;

int n, m;
int p[N], sz[N], d[N];

void init() {
	for (int i = 1; i <= n; i++) {
		p[i] = i;
		sz[i] = 1;
	}
}

int fnd(int x) {
	if (p[x] == x)
		return x;
	int rt = fnd(p[x]);
	d[x] += d[p[x]];
	return p[x] = rt;
}

void unn(int x, int y, int t) {
	x = fnd(x);
	y = fnd(y);
	if (x == y)
		return ;
	if (x == 1) {
		p[y] = 1;
		d[y] = t;
	}
	else if (y == 1) {
		p[x] = 1;
		d[x] = t;
	}
	else {
		p[x] = y;
		d[x] = 0;
	}
}

int l[N] = {0}, r[N] = {0};

struct Query {
    int u, v;
} q[N * 2];

bool ql[N] = {};
bool qr[N] = {};

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> l[i] >> r[i];
    for (int i = 1, p, h; i <= m; i++) {
        cin >> p >> h;
        q[i].u = p;
        if (h == 1)
        	q[i].v = l[p];
        else
        	q[i].v = r[p];
        
        if (h == 1)
        	ql[p] = true;
        else
			qr[p] = true;
    }
    
    init();
    for (int i = 1; i <= n; i++) {
        if (!ql[i] && l[i] != -1)
            unn(i, l[i], 0);
        if (!qr[i] && r[i] != -1)
            unn(i, r[i], 0);
    }

    for (int i = m; i >= 1; i--) 
        unn(q[i].u, q[i].v, i);
    
    for (int i = 1; i <= n; i++) {
        fnd(i);
        cout << d[i] - 1 << endl;
    }
    return 0;
}

标签：结点,int,sum,查集,合并,fnd
From： https://www.cnblogs.com/FLY-lai/p/18007919

并查集