本文参考《从一到无穷大》(作者:George $\cdot$ Gamow)第 $4$ 章
笔者知识浅薄,只是阅后拙见。可能有错漏之处,望高明的读者赐教。
什么是四维空间
众所周知,我们生活的三维空间中,确定物体的位置需要 $3$ 个坐标:长,宽,高。
四维空间,就是有 $4$ 个维度。那么,第四维是什么?
让我们想象一个情境:
有一天,你放学回家,兴奋地跟爸爸说:
“今天在物理课上,老师带我们去实验室做了一个有趣的实验,告诉我们飞机是怎么飞起来的。”
你的这句话完整的描述了一个“事件”(请允许我在这里加引号,后面会解释的)。
爸爸是如何确定这个“事件”的?
-
你告诉爸爸这个“事件”发生的时间(“今天在物理课上”)。
-
你告诉爸爸这个“事件”发生的地点(“实验室”)。
通过时间和地点,爸爸就能准确地确定你说的是物理老师做实验,而不是保洁阿姨打扫卫生(做完实验后一片狼藉)。
“地点”从物理的角度可以理解为“事件”的三维空间坐标。
那么“时间”自然可以理解为“事件”的第四维坐标。
通过三维空间坐标+一维时间坐标,就可以在我们生活的时空中确定一个“事件”。
小结
四维 = 三维空间 + 时间
如何理解四维物体
作为三维空间中的生物,我们无法想象一个真正的四维空间。
根据刚才的定义,时间是第四个维度。
所以,我们可以把四维物体理解为 一个三维物体在一段特定时间内的状态集合。
这样的四维物体,就可以描述为一个“事件”。
举个栗子:
(下文所有“立方体”均不考虑时间线的长度)
众所周知,三维立方体有 $8$ 个顶点,$12$ 条棱,$6$ 个面。
它的二维投影长这样:
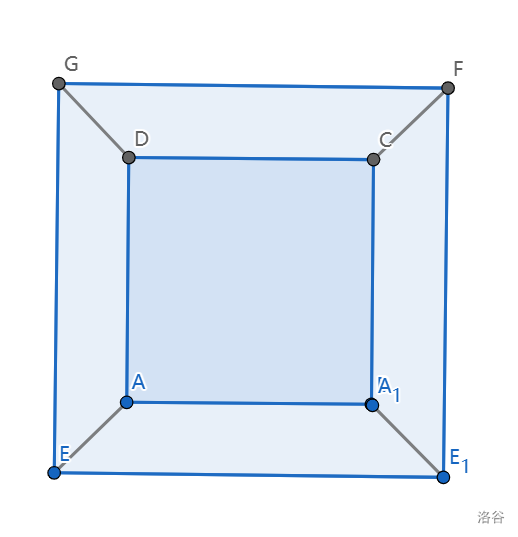
原谅我可怜的geogebra水平
(这不是我们常见的样子,但是为了理解四维立方体的投影,用这个更好)
现在我们尝试着用时空观来重定义这个东西。
9:30,数学老师在黑板上画了一个二维正方形 $HIJK$。
10:00,值日生把它擦了。
这个在9:30~10:00存在的二维正方形其实就是一个三维立方体。
或者说,正方形在时间维度上移动一段距离,它经过的轨迹形成立方体。
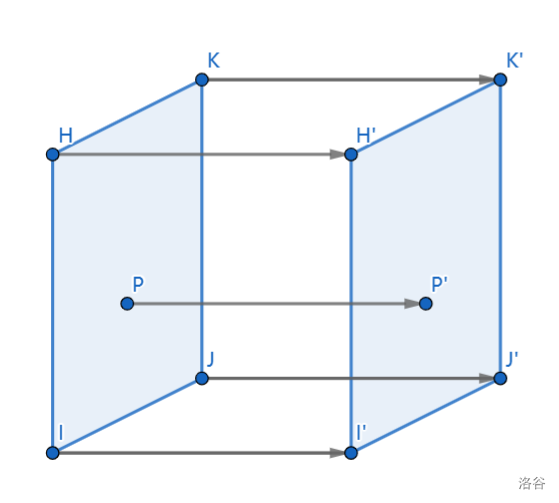
上图中水平方向代表时间,$HIJK$ 是9:30的正方形,$H'I'J'K'$ 是10:00的正方形,$HH',II',JJ',KK'$ 是时间线(第三维)。
这图看完应该懂了吧
接下来让我们开始幻想理解四维超立方体!
根据之前的经验,四维超立方体就是存在于特定时间的三维立方体。
5.1,数学老师让你做一个立方体模型(当然是三维的)。
6.1,你在一个奇怪的角落看到它,把它拆了并扔进垃圾桶。
于是我们有了一个四维超立方体(一个存在于5.1-6.1的三维立方体)
现在让我们来数一数这个四维超立方体有多少顶点、棱(线)和面。
-
点:5.1做出来的时候有 $8$ 个,6.1被拆的时候有 $8$ 个,一共 $16$ 个。非常显然。
-
线:5.1做出来的时候有 $12$ 条,6.1被拆的时候有 $12$ 条。在这一个月中,$8$ 个顶点分别引出 $1$ 条时间线,还有 $8$ 条。一共是 $32$ 条。
-
面:5.1做出来的时候有 $6$ 个,6.1被拆的时候有 $6$ 个。在这一个月中,$12$ 条边分别和顶点引出的 $2$ 条时间线组成$1$个面,还有 $12$ 个。一共是 $24$ 个。
是的我故意没放图,但是没有图也可以靠空想分析得出四维超立方体的一些特点,就像上面我们做的一样。
四维超立方体在三维空间的投影在屏幕上的投影:
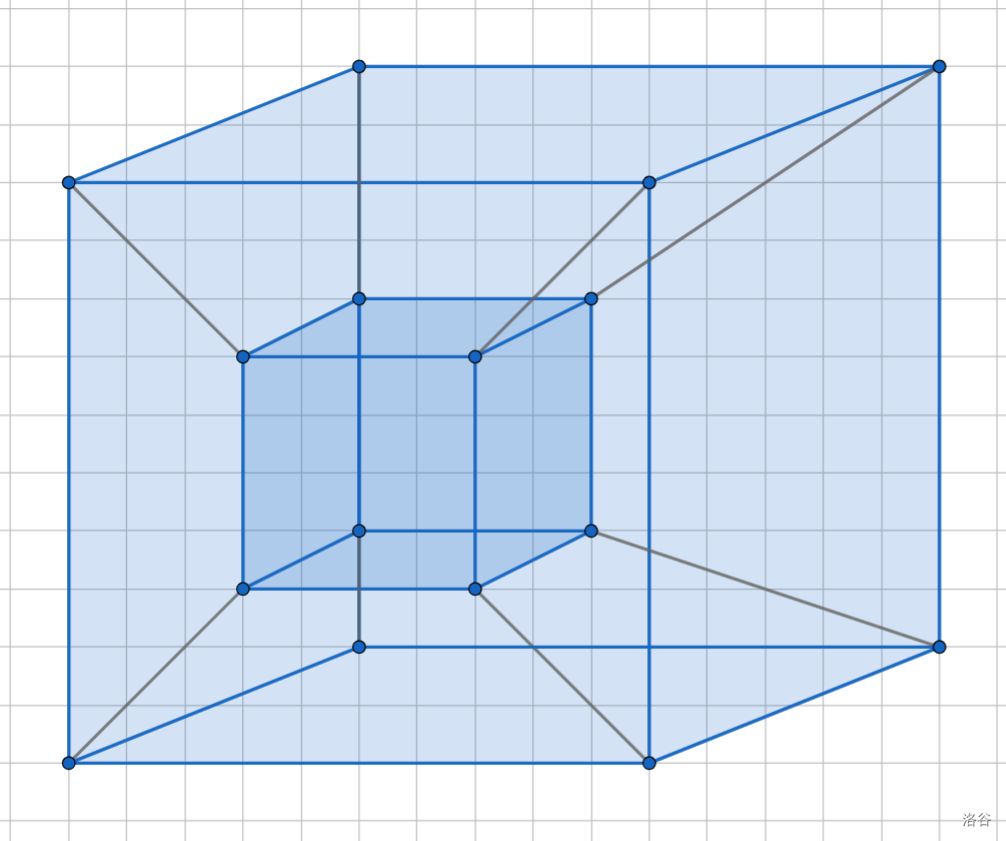
不信自己数一下顶点、边和面的数量
灰色是时间线
小结
四维物体=存在于特定时间段的三维物体
一些术语:
-
世界线:描述一个独立的粒子生命史的线(就是我
瞎编的“时间线”) -
世界带:组成复合物体的一束世界线(“$12$ 条边分别和顶点引出的 $2$ 条时间线组成$1$个面”就是一个世界带,整个超立方体也可以认为是一个世界带)
物理老师说写 $500$ 字我怎么写了这么多。。。
后面的时空等价和四维距离先咕了,等我有时间再写。
srds大概率会一直咕着