目录
前言
人工智能Alphago,成为最顶尖的围棋大师,不由得让人产生探索它背后的算法的兴趣。
在搜索空间巨大的围棋问题中,Alphago是通过什么算法能在较短的时间搜索每一个局面的(近似)最优解?
Alphago使用的算法如下:
- 蒙特卡洛树搜索
- 残余卷积神经网络 - 用于游戏评估和移动先验概率估计的策略和价值网络
- 用于通过自我游戏训练网络的强化学习
蒙特卡洛树搜索的适用范围
蒙特卡洛树搜索算法本质上是一种启发式搜索算法。
通过蒙特卡洛方法设计出较为准确的估价函数,使得问题在仅需迭代较少的次数就能得出(近似)最优解。
通常,在博弈问题中可以采用蒙特卡洛数搜索。
对于以下情况特别适用:
-
搜索空间特别大
-
采用传统方法(如:dp,贪心)直接设计出特别通用的估价函数(比如围棋)
蒙特卡洛树搜索的作用
蒙特卡洛树算法用于求当前局面如何决策是最优的。
算法有什么用要先明确。
在围棋中,每次再对手走完一步新局面产生的时候,都要重新运行蒙特卡洛树算法找出面对当前局面自己的最优解。
算法流程
前置:蒙特卡洛方法
用途:评估当前局面选取哪个决策最优
以围棋为例,难以直接用传统的dp,贪心等方法涉及出估价函数。
这时可以采用蒙特卡洛方法:
对于每个局面,随机轮流走棋,直到最后定出胜负。
在随机走大量次数的时候,取获胜次数最多的。
这时一个正确性难以保证的伪算法:
对于某个局面的某步决策,如果对方有几乎所有情况都将处于劣势,但是只要有一种情况必胜,那么这样的决策是绝对不可能采取的。
但是直接采用上面的蒙特卡洛方法恰恰容易采取这样的决策,因为这种决策胜率特别高。
流程
算法的设计思路:
类似人的下棋思维,在考虑当前步骤如何走的时候:
先根据棋感在脑中选取最可能的几步,再想对手对于自己走完这步的最可能的几种做法,
以此类推,求出自己认为对自己最有利的方法。
蒙特卡洛树采取类似的思路,用蒙特卡洛方法求估价函数的过程就是利用模拟自己走哪步,对手走哪步选出对自己最有力利的。
具体流程:
简单描述:
蒙特卡洛树搜索每次从根开始,依次进行选择,扩展,模拟,回溯四个步骤完成一次迭代。
在限定的时间或迭代次数中尽可能多的进行迭代,然后取从根开始评估次数最多的一个儿子即为求出的最优解。

将结点看成到某一步决策之后的局面,将边看成某种决策。
首先,明确每个点在每次迭代只会至多被遍历一次,每次迭代的目的是为了更新评估和胜利次数。
注意:评估次数只在每次迭代回溯时更新一条链。
对每个节点记录两个值:
\(w_v:\) v结点的胜利次数。
\(n_v:\) v结点的评估次数。
选择(算法的核心)
首先将结点分类:
- born:从来没有被评估过。
- active:自己之前被评估过至少一次,下一步所有可能的决策能到的点中存在born的点(从来没有被评估过的)。
- die:自己被评估过,在下一步所有可能的决策能到的点不存在born的点(从来没被评估过的)。
从根开始如果一个结点是die,就选儿子中最优的一个,搜索下去,知道找到第一个active的点,设为u。
在u的所有儿子中,随便选一个born的点进行第二步扩展。
如何在儿子中选择最优的:(蒙特卡洛树搜索算法的核心)
\[UCT(v)=w_v/n_v+c\sqrt{\ln(t)/n_v} \]\(t:\) 总评估次数,等于当前所有die和active点的 \(n_i\) 值之和。
\(c:\)参数,一般取\(\sqrt2\)
ln在c++中直接用\(log(t)\)
调参方法:c越大,评估次数越少的结点越可能评估到。
UCT的函数图像如下,由于后半段的存在使得某些一开始没有被评估到的结点也能被照顾到:

采用\(UCT\) 函数获得估价可以基本上解存在某种胜率高但是能让对手必胜的不合法情况。(尽可能避免了蒙特卡洛方法的弊端)
一开始,评估次数较少的时候胜率对选择一个结点的影响不那么大,随着评估次数的增加,胜率的影响越来越大。
UCT函数的核心是做到搜索次数少的时候不会完全受胜率影响,某些一开始胜率不高,但是后面胜率逐渐升高的最优决策能考虑到。
扩展
找到要扩展的点就把这个点建立出来,初值:\(n_i=w_i=0\)
然后进入第三步模拟。
模拟
采用蒙特卡洛策略,依次随机决策,直到最后确定胜负。
回溯
确定胜负后从扩展时新建立的点开始依次不断向父亲更新\(n_i,w_i\)的值。
若胜利:n++,w++
若失败:w++
若平局:n+=0.5
实现上,只需要存active和die的结点。
并且判断当前局面决策哪一步最优,只需要在到达一定的迭代次数之后取当前根结点评估次数最多的儿子即可。
优化
使用估价函数选择要扩展的点,而不是完全随机
按照传统方法涉及出估价函数,优先选择更好的结点扩展,从大到小。
每次将估价函数随机打乱一下可以确保估价一样的被随机访问到。
比如:五子棋第一步直接走中间是一定不会劣势的。
适当剪枝
在一些基本上不可能出现的决策可以不进行扩展。
比如不合法的情况,或者大概率处于劣势的情况(五子棋下在角上)
拓展
alphago采用了哪些优化?
1.模拟
alphago的模拟没有采用完全随机的方式,而是基于了一些既定策略和神经网络优化。
- 一种带有手工特征的浅层 softmax 神经网络:采用自定义快速走棋策略的标准走棋评估
- 估值网络:基于 13 层卷积神经网络的位置评估,训练自 Alpha Go 自我对弈的三千万个不同位置(没有任何两个点来自同一场游戏)
而 alphago zero 迈出了更远的一步,他们根本就不进行模拟,而是用一个 19 层 CNN 残差神经网络直接评估当前节点。(神经网络可以输出位置评估,得出每个位置的概率向量)
也就是说,利用神经网络,无需模拟,直接能算出每个位置的概率,可以说是直接消除了玄学问题。
2. 选择:
既然已经不是真的通过「模拟」的出赢的次数和已经评估的次数,那么我们之前通过 UCT 值的大小来向下搜索、选择一个未访问的叶子节点的方法也需要作出相应修改。
函数变为:
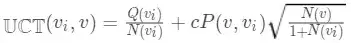
其中 \(UCT(v_i, v)\) 表示从状态(节点) \(v_i\) 转移到 v 的价值评估,\(P(v_i, v)\) 表示从状态 v_i 转移到 v 的概率,
或者用一个术语叫做「移动的先验概率」,这个概率是用策略网络训练出来的,基于人类游戏数据集的受监督学习。
有趣的是,在 Deepmind 的蒙特卡洛树搜索变种里,由于监督学习策略网络在实际中表现更好,因此它的结果被用来估测行动先验概率)。
那么强化学习策略网络的目的是生成 3 千万位置数据集,用于训练估值网络(估值网络就是我们上一步说的用来替代「模拟」的网络)。而在 Alphago Zero 中只有一个网络,它既是估值网络也是策略网络。
它完全通过从随机初始状态开始进行自我对弈训练。并行训练多个网络,在每个检查点,基于当前最优的神经网络,评选出最优的网络用来生成训练数据。
总结
蒙特卡洛搜索算法是一种采用蒙特卡洛方法的和UCT函数进行估价的启发式搜索算法。
采用优秀的估价函数使得在搜索空间中用较少的迭代次数就能得到(近似)最优解。
算法流程上:为了确定当前局面什么决策最优。经过多次从根开始的迭代,经过选择、扩展、模拟、回溯构建蒙特卡洛搜索树,选取访问次数最多的儿子为最优决策。
清晰记忆UCT函数的计算方法是关键。
优化方向:
-
按额外常规的方法设计估价函数,先访问最优的而不是完全随机。(为了保证估价相同的随机进行,可以先随机打乱。)
-
剪枝:减掉不合法和大概率不优
参考文献
蒙特卡洛树搜索最通俗入门指南 - 知乎 (zhihu.com)
蒙特卡洛树搜索 MCTS 入门_python class-CSDN博客
标签:估价,笔记,次数,搜索,蒙特卡洛,最优,评估 From: https://www.cnblogs.com/xulongkai/p/18001397