1.0写在前面
原题目为:浅谈后缀平衡树以及关于后缀平衡树非惰性删除操作正确性的思考和惰性删除操作的实现。

本文的主题是我对于后缀平衡树非惰性删除操作正确性的思考(就是上面那段话)。
感谢 jd 的图片。
2.0后缀平衡树的具体实现
2.1什么是后缀平衡树
是维护一个字符串后缀的数据结构,保证中序遍历后的结果为按照字典序排序后的结果。
2.2如何实现
毫无疑问,需要使用平衡树,因为它的特性(后面会说),推荐使用 Treap 或 SGT(本文使用)等期望树高 \(\log n\) 的平衡树(即高速平衡树)。
如果不会 SGT,可以参考一下这篇文章:link。
再提一下节点存储的信息,显然不能存一个字符串,否则空间直接到了 \(O(n^2)\),原地起飞,那我们可以将每个后缀的首字母在原字符串中的下标存进去,达到同样的效果,空间复杂度 \(O(n)\)。
2.3插入
和替罪羊树基本无异,关键在于比较。
大家都知道,两个字符串的比较,需要一位一位的比下去,故复杂度为 \(O(n)\),但如果采用这种方法,单次插入最坏复杂度为 \(O(n \log n)\),原地爆炸
考虑优化。
我们插入后缀时是从后往前插,那么,再插这一位时,那么它的下一位(字符串中),已经插入完毕,那么如果在比较是,如果两个后缀的首字符不同就比较他们后一位在平衡数中的排名,单次复杂度为 \(O( \log^2 n)\)。
但很显然,依然达不到 \(O(\log n)\) 的标准,那该怎么优化呢,来,我们思考一个问题,我们只需要知道两个字符串在树中的排名的比较结果,具体排名并不需要知道。
那我们给每一个节点定义一个区间 \([l,r]\),以及一个比较值,对于这个节点的比较值我们取 \(\frac{l+r}{2}\),那么它的左节点的区间为 \([l,\frac{l+r}{2}]\),比较值为 \(\frac{3l+r}{4}\),右节点为 \([\frac{l+r}{2},r]\),比较值为 \(\frac{l+3r}{4}\),很显然,对于根节点以及其左右节点的比较值,同样满足 BST 的性质,那我们就可以根据以上思路,来进行插入时的比较:
对于一个节点和一个插入的后缀,如果其首字符相同,就返回两个后缀分别删去首字母后的字符串在树中的比较值的比较结果,反之就返回首字母的字典序比较结果。
单次时间复杂度 \(O(\log n)\)。
bool cmp(int x,int y) { return (s[x]!=s[y]?s[x]<s[y]:t[x+1].tag<t[y+1].tag); }
void ins(int &x,int k,double dl,double dr) {
if (!x) {
x=k;
t[x].tag=(dl+dr)/2,t[x].ch[0]=t[x].ch[1]=0,t[x].sizt=1;// 新建节点
} else {
if (cmp(k,x)) ins(t[x].ch[0],k,dl,t[x].tag);// 字典序比本后缀串小
else ins(t[x].ch[1],k,t[x].tag,dr);// 字典序比本后缀串大
upd(x);
if (ifrbu(x)) rbu(x,dl,dr);// 重构
}
return;
}
2.4查询
这里的查询是查询一个字符串的出现次数(查询排名的什么直接把板子糊上去即可),先查询原字符串后加上一个字符 'Z'+1 的排名(包含原字符串的字典序最大的后缀),再求一下将原字符串最末位字符减一后再加上一个字符 'Z'+1(字典序比原字符串小的后缀中最大的后缀)的排名,两个结果一减即可。
因为不确定字符串是否出现过,只能暴力比较。
代码如下:
bool cmpp(char *str,int len,int x) {
for (int i=1;i<=len;i++,x=(x?x-1:0)) {
if (str[i]<s[x]) return 1;
if (str[i]>s[x]) return 0;
}
return 0;
}
int ask(int x,char *str,int len) {
if (!x) return 0;
if (cmpp(str,len,x)) return ask(t[x].ch[0],str,len);// 字典序比本后缀小
else return t[t[x].ch[0]].sizt+1+ask(t[x].ch[1],str,len);// 字典序比本后缀大
}
2.5重构
具体为什么这么操作下文会说(其实就是 SGT 的板子,但原板子有两种拍扁的方法,有一种不能用,下文会说)。
bool ifrbu(int x) { return t[x].sizt*A<(double)std::max(t[t[x].ch[0]].sizt+1,t[t[x].ch[1]].sizt+1); }// 判断是否需要重构
void rbuflatten(int x) {// 拍扁
if (!x) return;
rbuflatten(t[x].ch[0]);
lur[++luc]=x;
rbuflatten(t[x].ch[1]);
}
int rbubuild(int l,int r,double dl,double dr) {// 重建
if (l>r) return 0;
int mid=(l+r>>1);double dm=(dl+dr)/2;
t[lur[mid]].ch[0]=rbubuild(l,mid-1,dl,dm);
t[lur[mid]].ch[1]=rbubuild(mid+1,r,dm,dr);
t[lur[mid]].tag=dm;
upd(lur[mid]);
return lur[mid];
}
void rbu(int &x,double dl,double dr) { luc=0,rbuflatten(x),x=rbubuild(1,luc,dl,dr); }
3.0关于后缀平衡树非惰性删除正确性的思考
没错,现在才正式开始
注意,标题为思考,并非严谨的证明。
先把代码贴上:
void del(int &x,int k,double dl,double dr) {
if (!x) return;
if (x==k) {
if (!t[x].ch[0] or !t[x].ch[1]) {
int tmp=x;x=(t[x].ch[0]|t[x].ch[1]);
upd(x);
if (ifrbu(x)) rbu(x,dl,dr);
} else {
int y=t[x].ch[0],f=x;
while (t[y].ch[1]) {
f=y;
t[f].sizt--;
y=t[y].ch[1];
}
if (f==x) t[y].ch[1]=t[x].ch[1];
else {
t[y].ch[0]=t[x].ch[0];
t[y].ch[1]=t[x].ch[1];
t[f].ch[1]=0;
}
x=y;
t[x].tag=(dl+dr)/2;
upd(x);
if (ifrbu(x)) rbu(x,dl,dr);
}
} else {
if (cmp(k,x)) del(t[x].ch[0],k,dl,t[x].tag);
else del(t[x].ch[1],k,t[x].tag,dr);
upd(x);
if (ifrbu(x)) rbu(x,dl,dr);
}
return;
}
先来说明一下上述算法逻辑。
对于一棵后缀平衡树,如果要删除节点字典序大于本节点,就去右子树搜,反之去左子树搜,直到要删除节点为本节点,如果左右子树有一颗为空(或全为空),就将 x=(t[x].ch[0]|t[x].ch[1])(因为任何数或上 \(0\) 都不变),如果左右子树均不为空,就去找 \(x\) 的后继(即左子树中最大的节点),将其换上,复杂度均摊 \(O(\log n)\)。
哪里有问题呢,就是在找后继并将其换到指定节点时,不能保证后继的左子树为空,但事实呢,我们可以从重构树的形状考虑。
首先我们需要知道一个事情,对于一棵 SGT 其重构后的形状取决于 SGT 的节点的数量。
那么当一棵 SGT 的节点个数恰好等于 \(2^k-1\) 时,如下图:
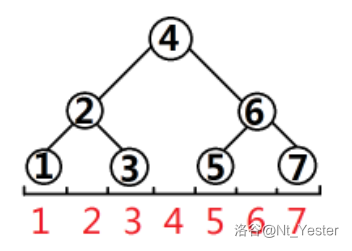
他重构后的形状就是一颗完美二叉树,那如果不是呢,假设它的节点个数为 \(2^k-3\) 难不成它的右子树正好缺三个节点??
当然不是,我们来看几组图(子树大小 \([4,8]\))。
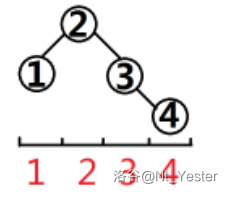
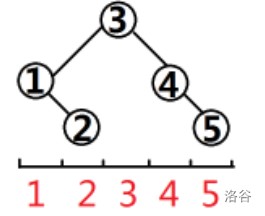

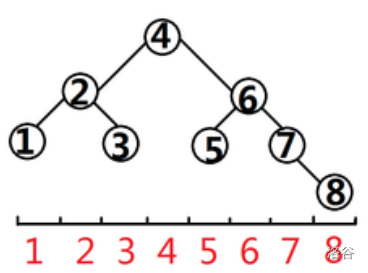
可以发现一棵树的形状是由它的左右子树大小决定的(子树大小等于 \(2^k-1\) 时也一样),其实这就像一个递归,
那递归总需要有一个递归边界吧,很显然,当子树大小为 \(3,2,1\) 时为边界,当子树大小为 \(3\) 时它长这个样子:
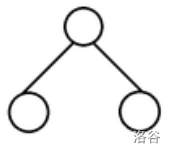
大小为 \(2\) 时长这个样子:
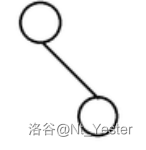
大小为 \(1\) 时长这个样子:

那么我们就可以按照以上三种情况推导出任意大小的 SGT 的形状。
显而易见,对一棵重构后的 SGT,它的所有没有右儿子的节点,一定没有左儿子,因为只有一个儿子的节点,一定是某个叶子节点的父亲(由上述三种情况推导而出)。
那么既然在树中没有一个节点只有左儿子没有右儿子,那么,我们在删除时,去找指定节点的前驱就不会出现把前驱的左子树扔掉,换上指定节点的左子树的情况。
所以非惰性删除操作没有错误。
但注意了,我们上面讨论的是重构后的结果,它所对应的重构算法是这么写的:
int rbubuild(int l,int r,double dl,double dr) {
if (l>r) return 0;
int mid=(l+r>>1);double dm=(dl+dr)/2;
t[lur[mid]].ch[0]=rbubuild(l,mid-1,dl,dm);
t[lur[mid]].ch[1]=rbubuild(mid+1,r,dm,dr);
t[lur[mid]].tag=dm;
upd(lur[mid]);
return lur[mid];
}
void rbu(int &x,double dl,double dr) { luc=0,rbuflatten(x),x=rbubuild(1,luc,dl,dr); }
而不是:
int rbubuild(int l,int r,double dl,double dr) {
if (l>=r) return 0;
int mid=(l+r>>1);double dm=(dl+dr)/2;
t[lur[mid]].ch[0]=rbubuild(l,mid,dl,dm);
t[lur[mid]].ch[1]=rbubuild(mid+1,r,dm,dr);
t[lur[mid]].tag=dm;
upd(lur[mid]);
return lur[mid];
}
void rbu(int &x,double dl,double dr) { luc=0,rbuflatten(x),x=rbubuild(1,luc+1,dl,dr); }
如果使用第二种,就会锅掉(比如我),因为他重构以后不保证所有没有右儿子的节点,一定没有左儿子,如:
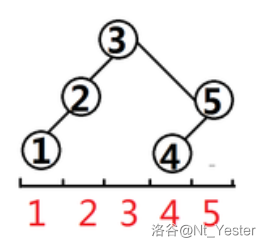
如果你用了,就会锅掉。
3.1关于插入
那万一插入时插入出来了一个有有左儿子,没有右儿子的节点呢。
那很显然,这棵树是失衡的,怎么证呢,令:
\[y_1=\alpha \times sizt_{fa}=\alpha \times (sizt_{lch}+sizt_{rch}+1)=\alpha \times (sizt_{lch}+1) \]\[y_2=sizt_{lch}+1 \]很显然 \(y_1\) 的斜率比 \(y_2\) 要小,且均为正比例函数,且 \(sizt_{lch} \geq 1\),所以两条射线在图像上没有交点,且 \(y_1\) 总是在 \(y_2\) 下面,故只要存在有有左儿子,没有右儿子的节点,那么就会被重构掉,成为只有右儿子没有左儿子的节点。
3.2另外
吐槽一下,按照以上说法,ifrbu 应该这么写:
bool ifrbu(int x) { return t[x].sizt*A<(double)std::max(t[t[x].ch[0]].sizt+1,t[t[x].ch[1]].sizt+1); }
但是这样写也能过板子:
bool ifrbu(int x) { return t[x].sizt*A<(double)std::max(t[t[x].ch[0]].sizt,t[t[x].ch[1]].sizt); }
只能说数据太水了。
4.0后缀平衡树惰性删除的实现
先咕着,明天补。
标签:dl,ch,浅谈,后缀,mid,int,平衡,dr,节点 From: https://www.cnblogs.com/NtYester/p/16783424.html