\(dp_{i, j}\) 表示第一个人走到 \(i\) ,第二个人走到 \(j\) 的方案数量。环上的情况先把每个点按照拓扑序排序,相同环上的点放在一起。
但是有可能在环上游走。
非常抱歉,昨天有很多东西是错的,以下内容感谢 \(\textrm{liuhangxin}\) 的帮助指正。
所以开一个辅助数组 \(g_{i, j}\) 用来记录 后面的人准备走出环上,前面的人刚走到新的环上的时候形成的局面 为 \((i, j)\) (如果两个人都在同一个环上那定义为两个人都刚刚走到新的环上),\(dp_{i, j}\) 用来记录 两个人准备走出环上的时候形成的局面 为 \((i, j)\) 。显然,\(dp\) 和 \(g\) 是互相转移的。容易把起点和终点的问题用建立虚点转化掉。
\(dp\) 向 \(g\) 的转移是容易的,所以关键的问题是 \(g\) 向 \(dp\) 的转移。
转移大概以下几类,以下默认 \(x\) 是在前面的那个:
\[\begin{aligned}\\& 如果 x 是单点 \\& g_{x, y} \rightarrow dp_{x, y} \\& \\& 如果 x 和 y 不在一个环上 \\& k * g_{x, y} \rightarrow dp_{pre_x, y} (环上的前一个点要特殊处理)\\& (k - 1) * g_{x, y} \rightarrow dp_{x', y} (otherwise)\\& \\& 如果 x 和 y 在一个环上,由于对称性哪个在前面无所谓 \\& \\& if(x = y) \\& \frac{k(k - 1)}{2}g_{x, x} \rightarrow dp_{x', y'} (x' = pre_x \lor y' = pre_x)\\& (\frac{k(k - 1)}{2} - 1)g_{x, x} \rightarrow dp_{x', y'} (otherwise,必须覆盖至少一次)\\& else \\& ① \frac{k(k + 1)}{2}g_{x, y} \rightarrow dp_{pre_y, pre_x} (刚好覆盖整个图一圈,注意上面那类没有这种情况)\\& ②(\frac{k(k + 1)}{2} - 1)g_{x, y} \rightarrow dp_{x', y'} (x' \in [x, pre_y], y' \in [y, pre_x] ,两个的路径不交,注意要排除掉前面那种情况。)\\& ③(\frac{k(k - 1)}{2} - 1)g_{x, y} \rightarrow dp_{x', y'} (x' \in [y, pre_x), y' \in [y, pre_x) ,两个的路径相交,但不覆盖整个圈)\\& ④(\frac{k(k - 1)}{2} - 1)g_{x, y} \rightarrow dp_{x', y'} (x' \in [x, pre_y), y' \in [x, pre_y) ,两个的路径相交,但不覆盖整个圈)\\& ⑤\frac{k(k - 1)}{2}g_{x, y} \rightarrow dp_{x', y'} (x' \in [y, pre_x), y' \in [pre_x, pre_y) ,两个的路径相交,覆盖整个圈)\\& ⑥\frac{k(k - 1)}{2}g_{x, y} \rightarrow dp_{x', y'} (x' \in [pre_y, pre_x), y' \in [x, pre_y) ,两个的路径相交,覆盖整个圈)\\& ⑦\frac{k(k - 1)}{2}g_{x, y} \rightarrow dp_{x', y'} (x' = pre_x \lor y' = pre_y) \end{aligned} \]这其中要特别注意的是 \(③④\) 两种转移的区间可能为空,要进行特判。我调了一早上 \(⑤⑥\) 两个区间其实是有交集的,具体见下图。在 \(k = 1\) 时,只存在转移 \(①②\) 。当然, \(k = 0\) 时答案为 \(0\) 。
有一些具有对称性的情况没写应该知道吧((,题目很良心的保证没有自环,算是减少了一下讨论量?
我知道这个很毒瘤,所以我放了一张图
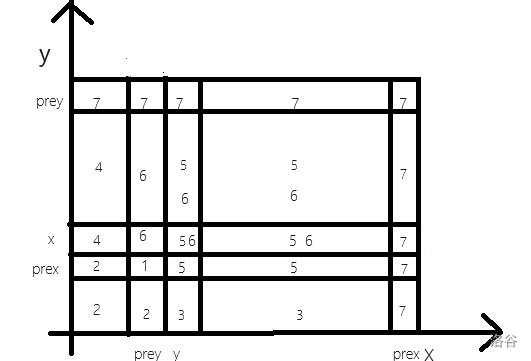
看到这张图,你肯定会这道题了。每个转移就是一个矩形加操作,非常的好写,非常的没有细节。