这篇题解中,我将从线段树的角度重新讲解,同时提出一个扩展。
我们可以用权值线段树维护最长连续段:线段树每个节点维护 \(L,R,M,S\) 分别表示这个区间的左边连续段长度、右边连续段长度、最大连续段长度、区间长度,这样就可以实现区间合并。
这样建的线段树如图:
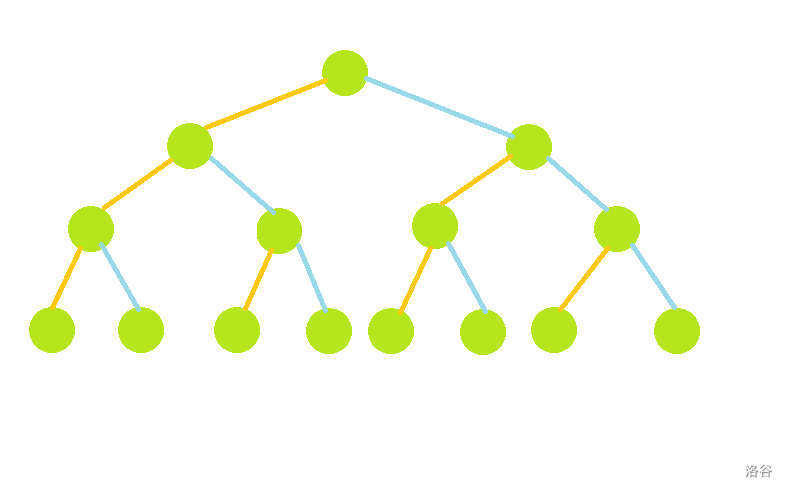
其中橙色线段代表左儿子,蓝色线段代表右儿子,下同。
为了方便后文叙述,“层”从下往上、从 \(0\) 开始编号,层的最大编号为 \(k\),每一层的节点从 \(0\) 开始编号。
考虑一个异或 \(x\) 的操作,比如 \(x=5\),如果固定底层的节点不变,则线段树会长这个样子:
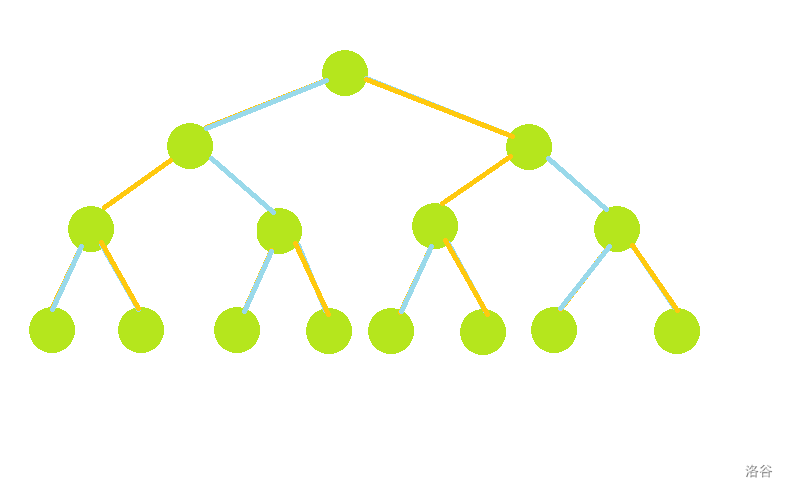
可以发现,实际上是把第 \(1\) 层和第 \(3\) 层的节点交换左右儿子。
实际上,对于异或 \(x\) 的操作,若 \(x\) 二进制第 \(i\) 位(从低到高,从 \(0\) 开始编号)为 \(1\),则将线段树第 \(i+1\) 层的左右儿子交换。
对于所有的异或 \(x\) 的操作,线段树的节点会有很多重合部分,把所有的操作的线段树建出来并合并,则会是这个样子:
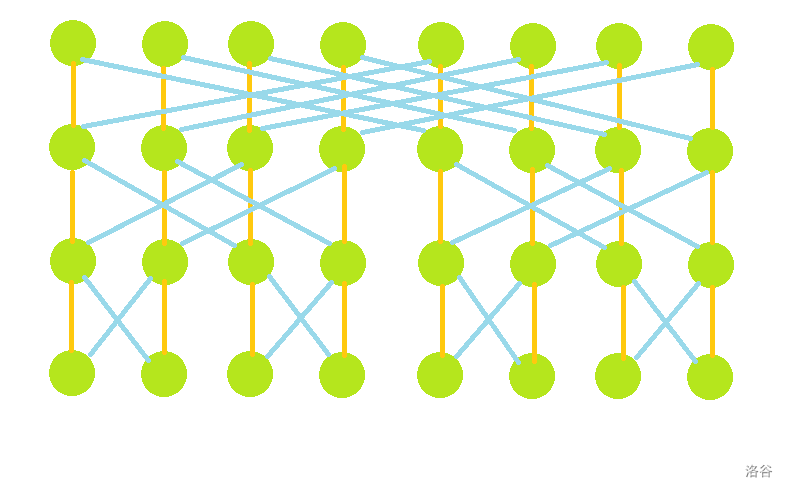
有几个性质:
- 对于第 \(i(i>0)\) 层第 \(j\) 个节点,它的左儿子是第 \(i-1\) 层第 \(j\) 个节点,右儿子是第 \(i-1\) 层第 \(j\bigoplus 2^i\) 个节点,其中 \(a\bigoplus b\) 表示 \(a\) 和 \(b\) 的按位异或。
- 对于第 \(k\) 层第 \(j\) 个节点,以这个点为根的线段树是异或 \(j\) 操作后的线段树。
对于本题,第 \(k\) 层节点的 \(M\) 值便是答案。
实际上,由于是线段树,它可以维护区间合并。也就是说,下标异或的背景下,可以 \(O(\log n)\) 求一般的可以区间合并的区间查询,但不支持快速修改(如图,一个底层节点涉及的节点是 \(O(n)\) 的)。
比如有以下问题:
- 这题的基础上可以加一个值域区间的限制。
- 给定长度为 \(2^m\) 的序列 \(a\),\(q\) 次询问给定 \(l,r,x\) 求 \(\max_{i=l}^r a_{i\bigoplus x}\),\(1\leq m \leq 20\),\(1\leq q \leq 2^{20}\),\(0\leq a_i\leq 10^9\)。
- 给定大小为 \(n\) 的集合 \(a\),\(q\) 次询问给定 \(x,k\),求 \(a\) 里的数异或上 \(x\) 后,集合的第 \(k\) 小值,\(1\leq n,q \leq 2^{20}\),\(0\leq a_i\leq 2^{20}\)。
#include <bits/stdc++.h>
using namespace std;
const int M = 21, N = 1 << 19 | 5;
int m = 19, n = 1 << m, q, t, x, y;
struct node{
int l, r, m, p;
}s[2][N];
void pushup(node &u, node &l, node &r)
{
u.l = l.p ? l.l + r.l : l.l;
u.r = r.p ? r.r + l.r : r.r;
u.m = max(l.r + r.l, max(l.m, r.m));
u.p = l.p & r.p;
}
int main()
{
scanf("%d%d", &q, &t);
while(q -- ) scanf("%d", &x), s[0][x] = {1, 1, 1, 1};
for(int i = 1, x = 1, y = 0; i <= m; i ++ , x ^= 1, y ^= 1)
for(int j = 0; j < n; j ++ )
pushup(s[x][j], s[y][j], s[y][j ^ (1 << i - 1)]);
while(t -- ) scanf("%d", &x), y ^= x, printf("%d\n", s[1][y].m);
return 0;
}