一. 后缀自动机的定义
SAM(Suffix Automaton) 是一种有限状态自动机,仅可以接受一个字符串的所有后缀。
如果您不懂自动机,那么换句话说:
SAM 是一个有向无环图。
称每个结点为状态,边为状态间的转移,每个转移标有一个字母,同一节点引出的转移不同。
SAM 存在一个源点 \(S\),称为初始状态,其它各结点均可从源点出发到达。也存在一个或多个终止状态 \(T\),每一条从 \(S\) 出发至 \(T\) 的路径所组成的字符串即为字符串的后缀。而对于这个字符串的每个后缀也必定在 SAM 的某条从 \(S\) 至 \(T\) 的路径上。
满足条件的同时,SAM 的点数是最少的。
接下来展示一个简单的 SAM:(以 abbb 为例)

红点为源点,蓝点为终止节点。箭头全部从左向右。
abbb 的所有后缀:
b: 1->5
bb: 1->5->6
bbb: 1->5->6->7
abbb: 1->2->3->4->7
二. \(\text{endpos}\) 数组
设 \(\text{endpos(t)}\),表示对于字符串 \(s\) 的任意一个非空字符串 \(t\),每一个 \(t\) 在 \(s\) 中出现的位置的右端。
如 abaabacaab,\(\text{endpos(ab)}=\{2,5,10\}\)。
显然会出现有两个不同子串 \(t_1,t_2\),而 \(\text{endpos}(t_1)=\text{endpos}(t_2)\),如 abaabacaab,\(\text{endpos(ab)=endpos(b)}=\{2,5,10\}\)。
那么我们称在 abaabacaab 里,ab,b 为同一个 \(\text{endpos}\) 等价类。
对于 \(\text{endpos}\),有几个引理:
引理 \(1:\) 对于一个字符串中的两个子串 \(u,v\),若 \(\text{endpos(u)=endpos(v)}\),那么一个将是另一个的后缀
显然成立。因为若 \(v\) 不是 \(u\) 的后缀,那么必定有一个 \(v\) 的最后一位字符就必然不等于 \(u\) 的最后一位字符。
例子:
aabab
endpos(b)=endpos(ab)={3,5}
u=ab,v=b
引理 \(2:\) 对于一个字符串的子串 \(u,v(|u|\ge|v|)\),那么必然有 \(\text{endpos}(u)\subseteq \text{endpos}(v)\) 或 \(\text{endpos}(u)\cap\text{endpos}(v)=\varnothing\)
即要么其中一个的 \(\text{endpos}\) 包含另一个的,要么两者的 \(\text{endpos}\) 没有交集。
显然有可能 \(\text{endpos}\) 两者无交集。而若两者的 \(\text{endpos}\) 有交集,那么不妨设 \(x\) 被 \(\text{endpos}(v)\) 包含且不被 \(\text{endpos}(u)\) 包含,那么由于两者 \(\text{endpos}\) 有交集,那么 \(v\) 的必然为 \(u\) 后缀,那么显然 \(x\) 必然被 \(\text{endpos}(u)\) 包含。
例子:
原串:abacabbacabca
//example1:
u=aba,v=aca
endpos(u)={3}
endpos(v)={5,10}
//example2:
u=aca,v=ca
endpos(u)={5,10}
endpos(v)={5,10,13}
引理 \(3:\) 每个 \(\text{endpos}\) 等价类里的子串升序排序后长度连续,且前一个串是这个串的后缀。
也很显然。若字符串 \(u,v\) 在同一个 \(\text{endpos}\) 等价类里,且 \(u\) 的长度严格小于 \(v\) 的长度且 \(u,v\) 长度不连续。由引理 \(1\) 显然 \(u\) 是 \(v\) 的后缀,那么 \(u,v\) 中间的那部分子串减去某个前缀后加上 \(u\) 显然亦为同一个 \(\text{endpos}\) 等价类里。
例子:
原串:acabaacbacaba
u=aba
v=acaba
endpos(u)=endpos(v)={5,13}
w=(c)+aba=caba,endpos(w)={5,13}
三. \(\text{parent tree}\)
虽然 \(\text{endpos}\) 还有引理,不过涉及到 \(\text{parent tree}\),就必要先讲这个。
考虑对于一个字符串 \(s\),如果我们在 \(s\) 前面加上一个字符 \(c\),那么会将 \(\text{endpos}(s)\) 分成若干份(也可能是一份)。
举个例子,还是 acabaacba,对于 ba,\(\text{endpos}(ba)=\{5,9\}\)。我们发现我们可以在 ba 前面加上 a 或 c,那么就变为 aba、cba,而 \(\text{endpos}(aba)=\{5\},\text{endpos}(cba)=\{9\}\),正好将 \(\text{endpos}(ba)\) 分成两份。
由于引理 \(2\),那么两个非后缀关系的子串的 \(\text{endpos}\) 必无交集,所以考虑对于一个字符串的子串的 \(\text{endpos}\) 等价集为节点,那么这些分割关系构成了树形结构。
由于此时是个森林,考虑用一个超级根聚合起森林。
而空串的等价集为全集(它无处不在),所以用空寂作为超级根。
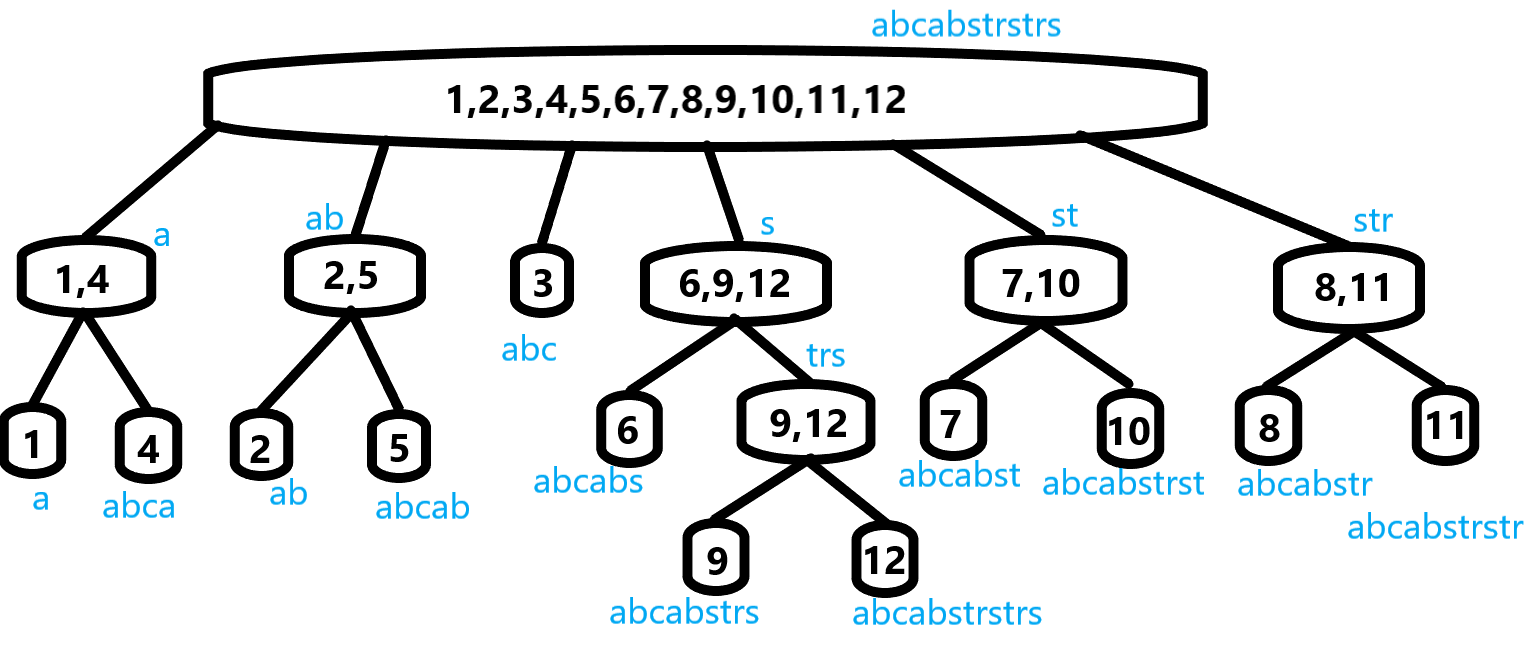
那么,我们以 abcabstrstrs 为原串建一个 \(\text{parent tree}\):
引入一个概念:我们称等价类 \(u\) 中的最长子串 \(len_u\) 指的是:该等价类 \(u\) 的所有子串中长度最长的子串。
那么每个节点旁边蓝色的就是代表当前节点(等价类)的最长子串。
结点中的数字为 \(\text{endpos}\) 集。
这时,我们就引出新的 \(\text{endpos}\) 引理:
引理 \(4\):若两个等价类 \(p,q\),\(p\) 在 \(\text{parent tree}\) 上是 \(q\) 的父亲,那么 \(p\) 的最长子串的长度 \(+1\),等于 \(q\) 的最短子串的长度。
我们考虑在一个等价类中的某个子串前再添加一个字符,显然,若选择的子串是这个等价类中的最长子串,形成的字符串就归于其儿子的等价类中,否则就仍在这个等价类中。
如果选择的是最长子串,那这个新形成的字符串肯定这个儿子等价类 中最短的一个。
引理 \(5:\) 等价类的数量是 \(O(n)\) 级别的。
如果说在一张图上表示一个字符串的所有子串,那么显然可以建 trie。
但是 trie 的节点数是 \(O(n^2)\) 的。
考虑 \(\text{parent tree}\) 的节点数量。
对于一个原串中的等价类,其中的最长子串 \(s\),在 \(s\) 前添加一个字符且新字符串仍为原串子串,那么对于新的字符串 \(t\),必然会得到若干个新的等价类,这一过程相当于 在 \(\text{parent tree}\) 中将父亲分裂成儿子。
考虑在 \(s\) 前加入两个不同字符,成为新字符串 \(t_1,t_2\),那么必定 \(\text{endpos}(t_1)\cap\text{endpos}(t_2)=\varnothing\),因为 \(\text{endpos}(t_1)\) 和 \(\text{endpos}(t_2)\) 必定不被包含。
所以,对于每个等价类集,最多分割出的大小不会超过原字符串集合大小。由于 \(\text{parent tree}\) 一共只有 \(n\) 个叶子结点,所以是 \(O(n)\) 的。
四. 后缀自动机的构建
后缀自动机的本质,是通过 \(\text{parent tree}\) 来维护的。
我们用 \(fa_u\) 表示在 \(\text{parent tree}\) 中 \(u\) 的直接父亲。
我们之前在 \(\text{parent tree}\) 已经知道了在子串前面加字符的做法,那么现在讨论关于在后面加字符的做法。
用 \(ch_{u,c}\) 表示在 \(u\) 结点对应的等价类的最长子串后面加上一个字符 \(c\) ,形成的新字符串所属的等价类对应的结点。
也就是 \(\text{endpos(ch}_{u,c})=\text{endpos}(len_{(\text{endpos(u)})+'c'})\)
可能有点绕,举个例子:
abcabstrs 的等价类在 \(u\) 节点,我们给它加上 t,就变成了 abcabstrst,其等价类在 \(10\) 节点。那么 \(ch_{u,'t'-'a'}=v\)。
SAM 的一个合法的连边方案应该满足,从源点出发到达点 \(u\) 经过的边形成的字符串,应该是点 \(u\) 的等价类的一个字符串,也就意味着,形成的字符串应该是点 \(u\) 的字符串的后缀。
我们先以 AABAB 为例子。
由于单张图片上传大小太大,所以我直接画出整个自动机 AABAB。显然现在的自动机有误,待会解释。
下图蓝色表示边上转移的字符,灰色表示点。

首先将空节点 \(1\) 加入。
然后加入字符 A,即 \(2\) 号节点。
加入 AA,即 \(3\) 号节点。由于 A 是 AA 的后缀,所以直接从 \(2\to 3\),转移为 A。
\(3\) 的后缀:
A: 1->2
AA: 1->2->3
加入 AAB,即 \(4\) 号节点。先连接 \(3\to 4\),转移是 B。但是 \(1,2\) 号节点都没有字符为 B 的出边,于是连接 \(1\to4,2\to4\),转移是 B。
\(4\) 的后缀:
B: 1->4
AB: 1->2->4
AAB: 1->2->3->4
加入 AABA,即 \(5\) 号节点。直接连接 \(4\to 5\)。
\(5\) 的后缀:
A: 1->2
BA: 1->4->5
ABA: 1->2->4->5
AABA: 1->2->3->4->5
加入 AABAB,此时与 \(4\) 时同理,连接 \(2\to 6,1\to 6\)。
\(6\) 的后缀:
B: 1->6
AB: 1->2->6
BAB: 1->4->6
ABAB: 1->2->4->5->6
AABAB: 1->2->3->4->5->6
检查一下这个自动机。从 \(1,2\) 号点出发,有两条字符为 B 的边,显然不符合 SAM 的性质。
我们考虑新建一个节点 \(7\),其字符串为 \(4,6\) 节点的最长公共后缀,即 AB。

我们考虑关于 \(7\) 的连边。
首先 \(1\to7,2\to7\),转移为 \(B\)。然后连接 \(7\to5\),转移为 A。这样,保证了 \(5\) 也满足。
\(4,5,6\) 的后缀:
4:
B: 1->7
AB: 1->2->7
AAB: 1->2->3->4
5:
A: 1->2
BA: 1->7->5
ABA: 1->2->7->5
AABA: 1->2->3->4->5
6:
B: 1->7
AB: 1->2->7
BAB: 1->7->5->6
ABAB: 1->2->7->5->6
AABAB: 1->2->3->4->5->6
我们看看 AABABA 的 SAM:

五. SAM 的代码实现
刚才我们已经模拟出了一个 SAM,现在我们考虑它如何用代码实现。
先放代码。代码中的 \(len,ch,fa\) 等如上文,只是用结构体表示第一维。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+3;
int n,last=1,tot=1,ans;
char s[N];
struct SAM{
int len,fa;
int ch[26];
SAM(){memset(ch,0,sizeof(ch));len=0;}
}sam[N];
inline void add(int c){
int p=last,np=++tot;
last=np;
sam[np].len=sam[p].len+1;
while(p&&!sam[p].ch[c]){
sam[p].ch[c]=np;
p=sam[p].fa;
}
if(!p)sam[np].fa=1;
else{
int q=sam[p].ch[c];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else{
int nq=++tot;
sam[nq]=sam[q];
sam[nq].len=sam[p].len+1;
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[c]==q){
sam[p].ch[c]=nq;
p=sam[p].fa;
}
}
}
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)add(s[i]-'a');
return 0;
}
一步一步讲解。
struct SAM{
int len,fa;
int ch[26];
SAM(){memset(ch,0,sizeof(ch));len=0;}
}sam[N];
inline void add(int c){
int p=last;
np=++tot;
last=np;
sam[np].len=sam[p].len+1;
//......
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)add(s[i]-'a');
return 0;
}
构建 SAM 的方法是增量法,即 SAM 每次吞进一个字符,对于这个字符而改变内部结构,再吞进下一个字符,以此类推。
每次吞字符的行为之间需要传递一些信息,除了以上提到的 \(fa\) 和 \(ch\) 照例保留外,还需要传递一个 \(last\) 变量,表示上一次添加字符后的串 \(s\) 所属的等价类。
显然,上一次加完字符后的串 \(s\) ,一定是 \(last\) 这个等价类的最长子串。
所以在最长子串 \(s\) 后加上了一个字符 \(c\) 形成了一个新串 \(t\),根据引理 \(4\),\(t\) 将会归到一个新的等价类里。
所以我们开一个新点 \(np\) ,表示 \(t\) 所属的新等价类对应的结点。
\(\therefore len_{np}=len_p+1\)
struct SAM{
int len,fa;
int ch[26];
SAM(){memset(ch,0,sizeof(ch));len=0;}
}sam[N];//将len、ch、fa存进结构体
inline void add(int c){
int p=last;//当前最长子串所在的等价类
np=++tot;//新等价类
last=np;//更新 last
sam[np].len=sam[p].len+1;//引理4得
//......
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)add(s[i]-'a');//增量法
return 0;
}
inline void add(int c){
//......
while(p&&!sam[p].ch[c]){
sam[p].ch[c]=np;
p=sam[p].fa;
}
//......
}
遍历新串后缀,到第一个出现过的子串为止。
每当我们加入一个新字符,可能之前某些子串的出现位置(即 \(\text{endpos}\) 中的元素)就会变多。
比如当前加到第 \(n\) 位,有些新子串从来没出现过,需要多开一个 \(\{n\}\) 的等价类包含它们;有些新子串曾经出现过,它们的 \(\text{endpos}\) 中就多一个 \(n\) 。
这一段就是找到这些新子串的出现位置。对于新子串 \(t\),它必然是加上新字符前的原字符串的某后缀,再拼接上我们现在加的这个字符 \(c\)。
既然是后缀关系,对于拼上 \(c\) 的新串 \(t\),一定存在某长度的后缀,使得长度小于它的其它后缀都出现过。
比如 ABCABSTRSTR,给它加上一个 S,那么 只有ABCABSTRSTRS,BCABSTRSTRS,CABSTRSTRS...TRS,RS,S 以及 \(\varnothing\) 的 \(\text{endpos}\) 会发生改变。
然而,在这些子串中,TRS,RS,S 和 \(\varnothing\) 在之前就出现过,所以它们在它们原有的 \(\text{endpos}\) 的基础上加上 \(11\);而其余的就直接归类于 \(11\)。
为了区分这些子串之前有没有出现过,考虑遍历后缀,找到这个第一个出现过的后缀。
又因为在一个字符串前面加一个字符等价于将其 \(\text{endpos}\) 分裂,即在 \(\text{parent tree}\) 上分裂出子树。
反过来看,相当于删去前面的字符,那么就相当于在 \(\text{parent tree}\) 上原地不动(不发生分裂)或者往上跳 \(fa\)。
所以通过跳 \(fa\) 来遍历后缀。
inline void add(int c){
//......
while(p&&!sam[p].ch[c]){//p的判断表示防止跳出parent tree;!sam[p].ch[c] 表示p+'c'的最长子串是否曾经出现过
sam[p].ch[c]=np;//如果没有出现过,那么它的endpos直接为np
p=sam[p].fa;//跳fa操作
}
//......
}
inline void add(int c){
//...
if(!p)sam[np].fa=1;
else{
int q=sam[p].ch[c];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else{
int nq=++tot;
sam[nq]=sam[q];
sam[nq].len=sam[p].len+1;
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[c]==q){
sam[p].ch[c]=nq;
p=sam[p].fa;
}
}
}
}
分三个部分。
- 根作为它的父节点
if(!p)sam[np].fa=1;
这种比较容易,从 \(p\) 向上爬,如果一直爬到了根还没有 break,那么说明没有节点能做它的 \(fa\),那么只有根可以,那么直接认根做父节点。
- \(len_q=len_p+1\)
int q=sam[p].ch[c];
else if(sam[q].len==sam[p].len+1)sam[np].fa=q;
设 \(q=sam_p.ch_c\),我们需要知道 \(p\) 的最长子串 \(+c\) 是否是 \(q\) 的最长子串。
换句话说:
\(p\) 在第一个有 \(c\) 边的祖先停下了,\(q\) 即为 \(p\) 的 \(c\) 出边到达的节点。
其中一种情况是 \(p\) 的最长子串 \(+c\) 就是 \(q\) 的最长子串。
因为这个串是最长子串,显然同等价类的其它子串都是它的后缀。所以它的后缀也会添加 \(\{n\}\)。
那么我们直接令这整个集合 \(q\) 成为 \(np\)(它对应 \(\{n\}\) 等价类)的 \(fa\) 即可。
举个例子:
比如现在到了 ABCABSTRS,要加入 T,\(np\) 的最长子串即为 ABCABSTRST,在等价类 \(\{10\}\)。
然后我们通过跳 \(fa\),算出了最长的曾经出现过的后缀 ST。
那么 \(q\) 即为 \(sam_{p,'t'-'a'}\),然后这个等价类最长子串就是 ST,所以 \(fa_{np}=q\),也就是在 \(\text{parent tree}\) 上 ST 是 ABCABSTRST 的父亲,也就是说 \(\{7,10\}\) 是 \(\{10\}\) 父亲。
int q=sam[p].ch[c];//取出q
else if(sam[q].len==sam[p].len+1)//q的最长子串=p的最长子串+c,即q的长度=p长度+1
sam[np].fa=q;//q成为np的fa
- \(len_q≠len_p+1\)
else{
int nq=++tot;
sam[nq]=sam[q];
sam[nq].len=sam[p].len+1;
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[c]==q){
sam[p].ch[c]=nq;
p=sam[p].fa;
}
}

比如像 \(7\) 号节点。
显然 \(len_p+1\) 不总是一定为 \(len_q\)。
既然我们需要一个可以做 \(p\) 的父亲的点,那么我们就构造一个 \(u\) 的父节点,设它为 \(nq\)。
所以 \(nq\) 的最长子串就是 \(p\) 的最长子串 \(+c\)。
\(\therefore len_{nq}=len_p+1\)
\(nq\) 在分裂以前与 \(q\) 的差别在且仅在于 \(\text{endpos}\),而在后面加一个字符能转移到哪里,就不在 \(\text{endpos}\) 决定的范围内了。
考虑 \(ch\),它表示的是在后面加字符后归在的等价类,显然 \(ch_{nq}\) 和 \(ch_q\) 其实没有区别。那么直接令 \(nq\) 继承 \(q\) 的 \(ch\)。
最后是 \(fa\)。\(fa_q\) 之前和 \(q\) 在树上成父子关系,根据引理 \(4\),当时的 \(len_{fa_q}+1\) 必然等于 \(q\) 最小子串长度。
而 \(q\) 的最小子串在 \(nq\) 等价类里。
\(fa_{nq}=fa_q,fa_q=fa_{np}=nq\)
举个例子:
aabab 在加入第二个 b 时子串 ab 已经存在,所以 ab 的 \(\text{endpos}\) 集合变为 \(\{3,5\}\),这样原来第一个 b 表示 aab,ab,b,它们的 \(\text{endpos}\) 都是 \(3\),而现在只能表示 aab 的 \(\text{endpos}\) 是\(3\),而 ab,b 的 \(\text{endpos}\) 是 \(3,5\),所以需要一个新的点来维护,同时这样操作也保证了如果在后面加入 c,只会增加 c,bc,abc 的 \(\text{endpos}\) 而不会增加 aabc 的 \(\text{endpos}\)。
但是有些结点的 \(ch_c\) 指向的是 \(q\),而分裂后,这些 \(ch_{c}\) 需要指向 \(nq\)。
所以考虑对于 \(p\) 不断往上 \(fa\)。判断条件为 \(sam_{p,ch_c}=q\)。
即 \(q\) 的 \(\text{endpos}\) 不包含 \(\{n\}\),而 \(p\) 的最长子串 \(+c\) 的 \(\text{endpos}\) 包含 \(\{n\}\)。
所以令这条边连向新的节点 \(nq\),不断操作即可。
\(nq\) 的出边就是 \(q\) 的出边,然后 \(q\) 的所有除地面上地链上地入边都搬到了 \(nq\) 上面去。
这就讲完了代码部分。
六. 复杂度
七. 练习题目
给你一个长为 \(n\) 的字符串,求不同的子串的个数。
\(n\le 10^5\)
对于一个给定的长度为 \(n\) 的字符串,求出它的第 \(k\) 小子串。
标签:子串,SAM,sam,后缀,text,len,fa,endpos,自动机 From: https://www.cnblogs.com/trsins/p/17970738\(1≤n≤5×10^5\)