标签：suf 后缀 笔记 数组 SA 排序 rk

后缀数组 SA 学习笔记

后缀数组处理字符串后缀排名，公共子串类问题十分优秀，可以在部分情况下替代后缀自动机（SAM），本文主要讲解后缀数组的实现过程和部分例题。

正文

定义

后缀：从 \(i\) 开始到字符串结束的一个特殊子串，本文用 \(suf(i)\) 表示从 \(i\) 开始的后缀。

后缀数组 SA：SA 是一维数组，\(SA_i\) 表示所有后缀按字典序排序之后，第 \(i\) 名的后缀的开始位子，即 \(suf(SA_i)\) 在所有后缀中字典序排序是第 \(i\) 名。

名次数组 rk：rk 是一维数组，\(rk_i\) 表示后缀 \(suf(i)\) 和所有后缀按字典序排序后的排名。

倍增算法

前置知识：基数排序。

使用倍增方法，对字符开始的 \(2^k\) 长度的子字符串进行排序，求出其 rk 值。（这里 rk 允许相同）

当 \(2^k\) 大于 \(n\) 以后我们的后缀数组 SA 已经求出。

在求 \(2^k\) 长度的排序时，\(2^{k-1}\) 的排序已经求出，一个长度为 \(2^k\) 的段可以由两个长度为 \(2^{k-1}\) 的段合并得到。

那么把从 \(i\) 开始的前 \(2^{k-1}\) 位之前的排序结果的 rk，看做第一关键字，把后 \(2^{k-1}\) 的排序结果看做第二关键字，对关键字排序从而求出整个排序结果。

附一张 2009 年集训队论文的图：

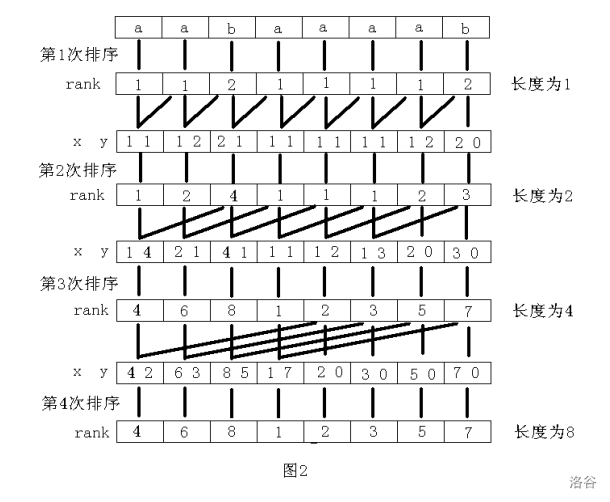
这里的 \(x\) 为第一关键字，\(y\) 为第二关键字。

在排序时使用基数排序，可以利用上次的排序结果，直接排序好第二关键字。

#include<bits/stdc++.h>
using namespace std;

const int maxn=2e6+5;

int n,m=128;
int sa[maxn],rk[maxn],b[maxn],tmp[maxn];

char s[maxn];

int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);
    for(int i=1;i<=n;i++) ++b[rk[i]=s[i]];
    for(int i=1;i<=m;i++) b[i]+=b[i-1];
    for(int i=n;i;i--) sa[b[rk[i]]--]=i;
    for(int i=1;i<=n;i++) tmp[i]=rk[i];
    int t=0;
    for(int i=1;i<=n;i++)
    {
        if(tmp[sa[i]]==tmp[sa[i-1]]) rk[sa[i]]=t;
        else rk[sa[i]]=++t;
    }
    m=t;

    for(int l=1;l<n;l=l<<1)
    {
        int t=0;
        for(int i=n-l+1;i<=n;i++) tmp[++t]=i;
        for(int i=1;i<=n;i++) if(sa[i]>l) tmp[++t]=sa[i]-l;
        for(int i=1;i<=m;i++) b[i]=0;
        for(int i=1;i<=n;i++) b[rk[tmp[i]]]++;
        for(int i=1;i<=m;i++) b[i]+=b[i-1];
        for(int i=n;i;i--) sa[b[rk[tmp[i]]]--]=tmp[i];//基数排序

        for(int i=1;i<=n;i++) tmp[i]=rk[i];//读取上次排名，修改本次rk
        t=0;
        for(int i=1;i<=n;i++)
        {
            if(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+l]==tmp[sa[i-1]+l]) rk[sa[i]]=t;
            else rk[sa[i]]=++t;//过程中允许排名相同
        }
        m=t;
    }
    for(int i=1;i<=n;i++) printf("%d ",sa[i]);
}

SA-IS

先留个坑

关于后缀数组的应用

定义

height 数组：\(height_i=LCP(suf(SA_i),suf(SA_{i-1}))\)。

求 height 数组

如果直接去求 height 数组是 \(O(n^2)\) 的，并没有利用 SA 的优秀性质。

但这里有一个妙不可言的证明，可以把两者联系起来。

排序后，越接近的两个后缀，他们的 \(LCP\) 肯定越大。数学语言就是 \(|rk_i-rk_j|<|rk_i-rk_k|\)，有 \(LCP(suf(i),suf(j))\ge LCP(suf(i),suf(k))\)。

设 \(h_i=height_{rk_i}\)，我们有：

\[h_i\ge h_{i-1}-1 \]

画一张图：

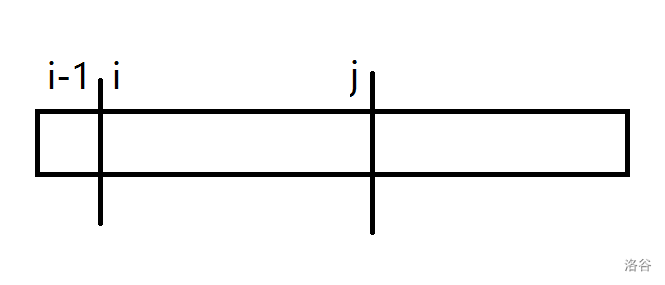
其中 \(s_{i-1}\) 到 \(s_j\) 是的长度 \(j-(i-1)+1\) 等于 \(h_{i-1}=height_{rk_{i-1}}\)。

也就是说，\(s_{i-1}\) 到 \(s_j\) 是 \(suf(i-1)\) 和 \(suf(i-2)\) 的最长公共后缀（\(LCP\)）。

那么 \(s_i\) 到 \(s_j\) 这一段区间肯定能够找到和其一样的区间，所以 \(h_i=height_{rk_i}\) 至少为 \(j-i+1\)，即 \(h_{i-1}-1\)。

得证。

height 数组的实际运用

height 数组的实际运用有很多，这里先提出一个运用，后面例题再分析：

求 \(LCP(suf(i),suf(j))\ (i\neq j)\)。

不妨设 \(rk_i < rk_j\)。

理解一下，有

\[LCP(suf(i),suf(j))=\min_{k=rk_i+1}^{rk_j} height_k \]

上图：

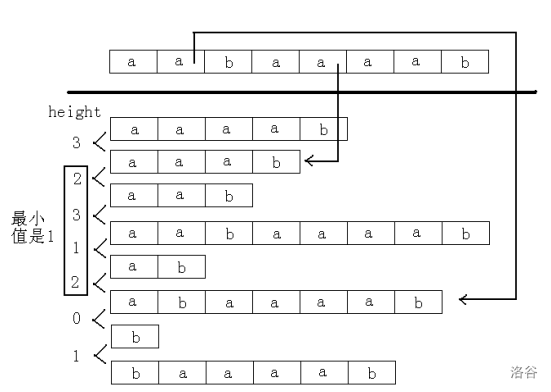
不难证明上述结论，留作读者自己思考。

例题

下次补。

标签：suf,后缀,笔记,数组,SA,排序,rk
From： https://www.cnblogs.com/binbinbjl/p/17964417