Meaning
在二维平面内,有位置不同且不存在三点共线的 \(R\) 个红点和 \(B\) 个黑点,判断是否能用一些互不相交的线段连接每一个点,使得每条线段的两端都分别是黑点和白点。
Solution
当 \(R\ne{B}\) 时,显然无法实现红点与黑点的两两组合,故题干所述的情况一定不存在。
当 \(R=B\) 时,我们考虑一种连线的方式(事先给所有红点带上 \(1\) 的权值,给所有黑点带上 \(-1\) 的权值):先找到纵坐标最小的一列点,以其中任意一个点作为坐标原点重新构建平面直角坐标系。接下来,以这个坐标原点为顶点,向 \(y\) 轴正方向做一条射线。然后,将射线上除端点外所有点的权值累加起来,并将该射线绕着端点顺时针旋转,直到该射线过平面中其他的点。重复此操作并累加权值,直到累加值与端点的权值之和为 \(0\)。
由于射线最后扫过的点可以为累加值做出与端点相反的贡献,使得累加值为端点权值的相反数,故最后扫过的点一定与端点异色。而由于保证任意三点不共线,可以在这个点与端点之间连一条符合题意的线段。而且,由于顶点权值与累加值之和为 \(0\),所以这条线段上方、下方的红点与黑点的个数均分别相等。将线段上方、下方的两部分取出,重复上述的操作,直到某一部分只剩下一个红点和一个黑点。由于在这几个部分独立且均满足 \(R=B\),所以这一组操作可以完成,且没有任何两条线段相交。
综上所述,当 \(R=B\) 时,题干所述的情况一定存在。
下面,我们利用样例 \(1\) 来演示一下上述过程。
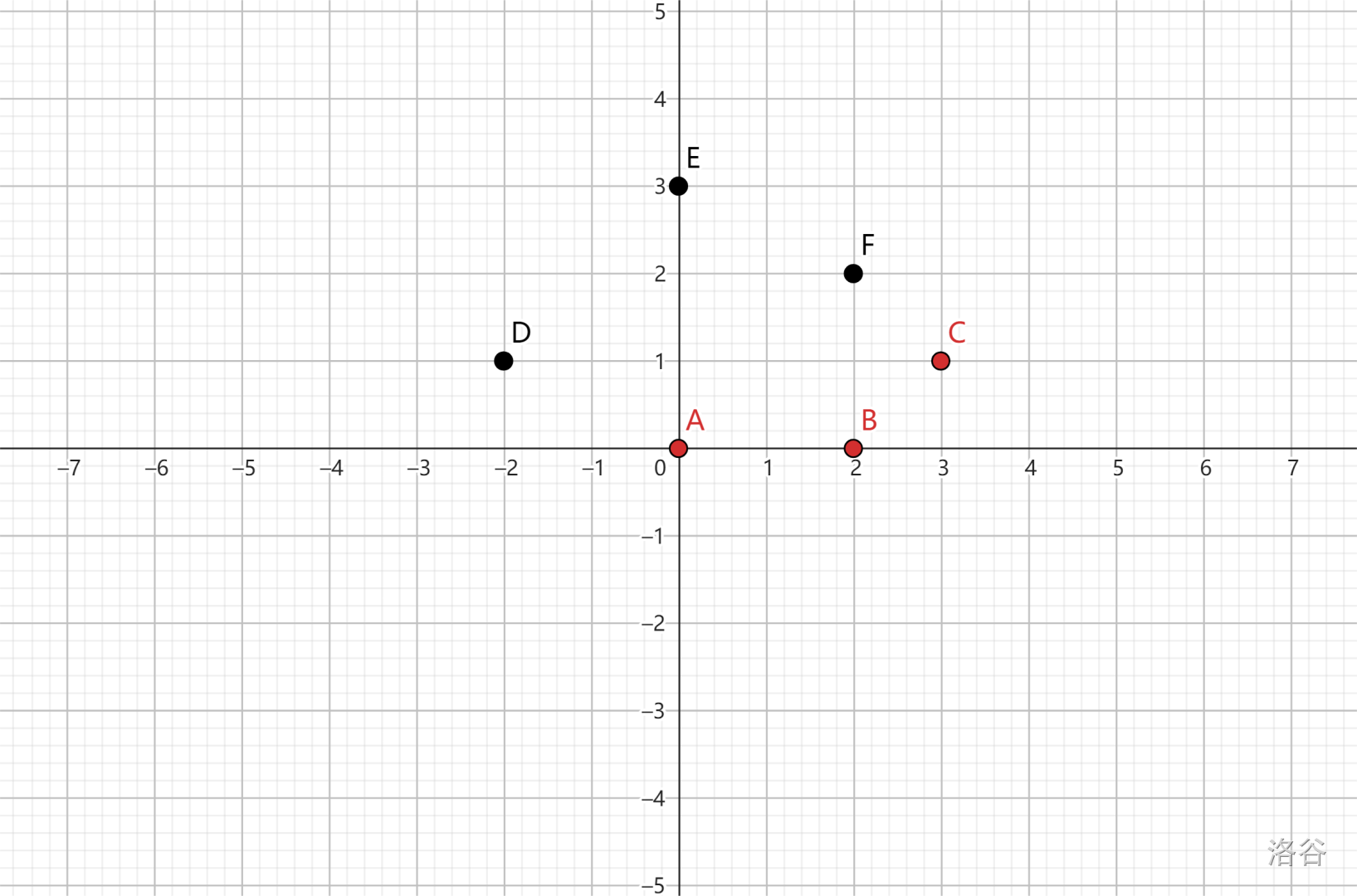
如图,我们找到点 \(D\) 并进行扫描。
- 射线 \(DE\),累加值 \(-1\),端点权值 \(-1\),扫描继续。
- 射线 \(DF\),累加值 \(-2\),端点权值 \(-1\),扫描继续。
- 射线 \(DC\),累加值 \(-1\),端点权值 \(-1\),扫描继续。
- 射线 \(DB\),累加值 \(0\),端点权值 \(-1\),扫描继续。
- 射线 \(DA\),累加值 \(1\),端点权值 \(-1\),扫描结束。
因此,我们连接 \(DA\)。

由于没有下半部分,只考虑上半部分。找到新的坐标原点为点 \(E\)。经过扫描,连接 \(EB\)。
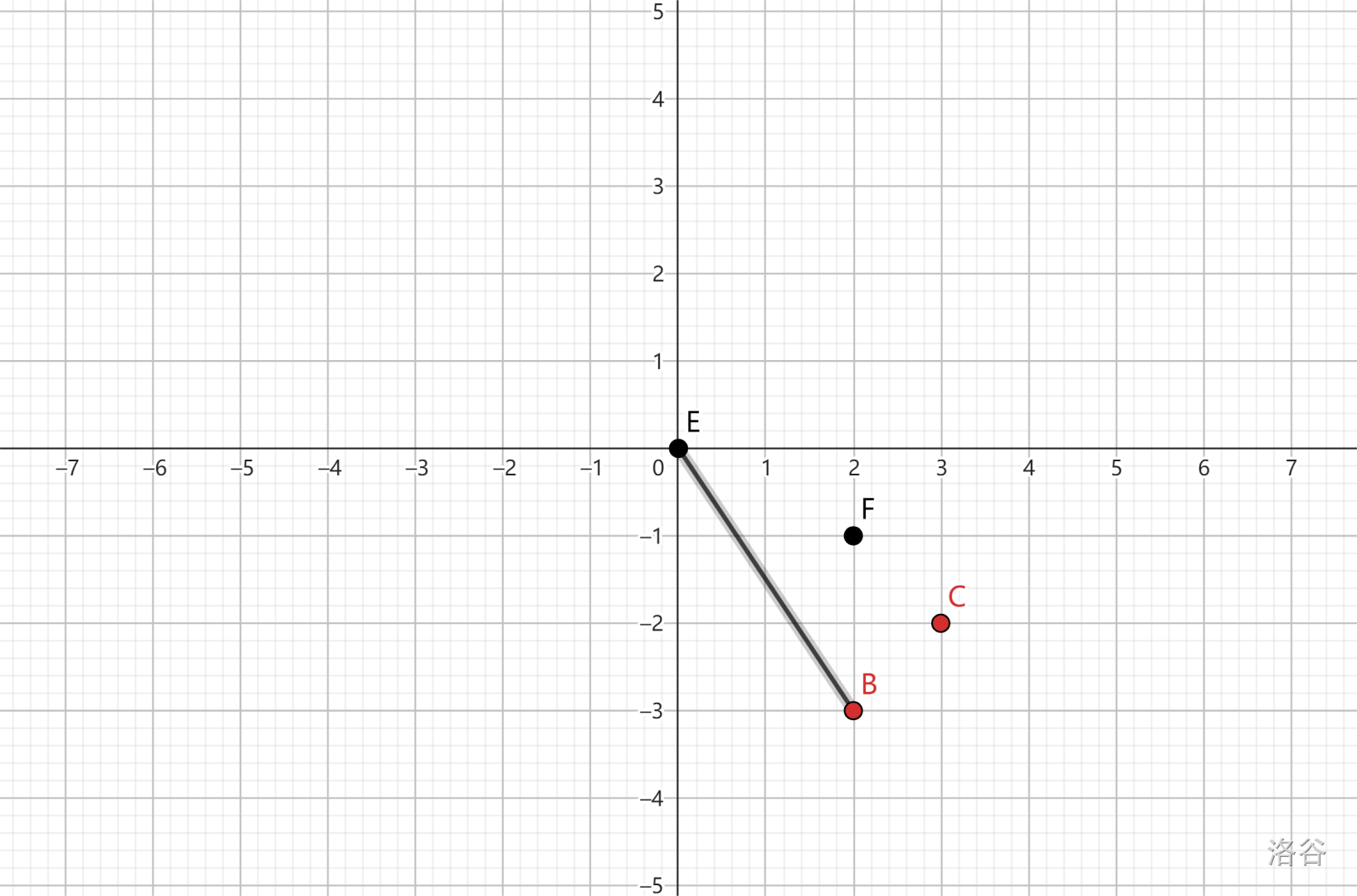
此时只剩下红点 \(C\) 和黑点 \(F\),故存在题干所述的情况。
Code
#include<bits/stdc++.h>
using namespace std;
int main(){
int b,r,x,y;
scanf("%d%d",&r,&b);
for(int i=1;i<=r;++i){
scanf("%d%d",&x,&y);
}
for(int i=1;i<=b;++i){
scanf("%d%d",&x,&y);
}
if(b==r)
printf("Yes");
else
printf("NO");
}