题目传送门

前置知识

二分答案 | 并查集

解法

对条件的合法性判断其他题解已经讲得很明白了，这里不再赘述。这里主要讲一下用并查集实现黑白染色问题。

以下内容称被覆盖为黑色，不被覆盖为白色。

本题因为是单向染色，即从白到黑，故可类似 luogu P1840 Color the Axis 和 D 的并查集或线段树做法；如果是双向染色，则需要 CF915E Physical Education Lessons 的珂朵莉树或线段树做法。

luogu P1840 Color the Axis 在染色的过程中，我们只关注白色的数量。题意可以转换为给定 \(n\) 棵树组成的森林，每次操作将 \([l_i,r_i]\) 的树删除，求每个操作执行后剩余的树的个数。删除第 \(i\) 棵树等效替代于将第 \(i\) 棵树和第 \(i-1\) 或第 \(i+1\) 棵树合并为一棵树。为方便理解，我们将第 \(i\) 棵树和第 \(i+1\) 棵树合并为以 \(i+1\) 为父亲节点，以 \(i\) 为子节点的一棵（子）树。本题要求求该位置是否为黑色，但同样可以用类似的方法进行合并。

• 例子：设 \(n=5,m=1\) 时操作为将 \([2,4]\) 的树删除。过程如下
  

  

  

  

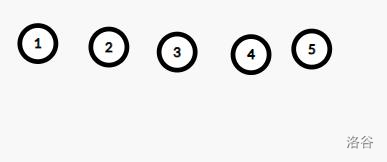
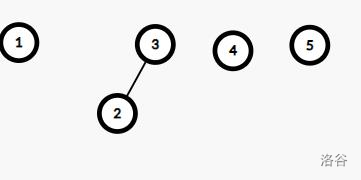
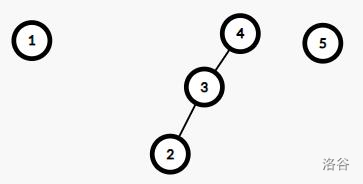
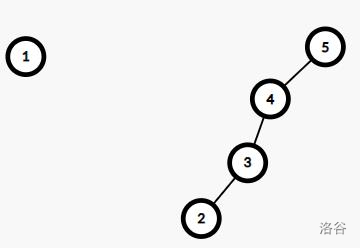
• 这里可以感性理解下。作者语文功底不是很好，可能解释不是很清楚。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define ull unsigned long long
#define sort stable_sort 
#define endl '\n'
struct node
{
	int l,r,x;
}a[1000002],b[1000002];
int f[1000002];
bool cmp(node a,node b)
{
	if(a.x==b.x)
	{
		if(a.l==b.l)
		{
			return a.r<b.r;
		}
		else
		{
			return a.l<b.l;
		}
	}
	else
	{
		return a.x>b.x;
	}
}
int find(int x)
{
	return (f[x]==x)?x:f[x]=find(f[x]);
}
bool check(int mid,int n)
{
	int i,j,maxl,maxr,minl,minr,ls;
	for(i=1;i<=n+1;i++)//第n棵树要和第n+1棵树合并
	{
		f[i]=i;
	}
	for(i=1;i<=mid;i++)
	{
		b[i].l=a[i].l;
		b[i].r=a[i].r;
		b[i].x=a[i].x;
	}
	sort(b+1,b+1+mid,cmp);
	ls=b[1].x;
	maxl=minl=b[1].l;
	maxr=minr=b[1].r;
	for(i=2;i<=mid;i++)
	{
		if(ls==b[i].x)
		{
			maxl=max(maxl,b[i].l);
			minl=min(minl,b[i].l);
			maxr=max(maxr,b[i].r);
			minr=min(minr,b[i].r);
			if(maxl>minr)
			{
				return false;
			}
		}
		else
		{ 
			if(find(maxl)>minr)
			{
				return false;
			}
			else
			{
				for(j=find(minl);j<=maxr;j=find(j+1))//将第j棵树和第j+1棵树合并为同一棵树
				{
					f[j]=f[j+1];
				}
				ls=b[i].x;
				maxl=minl=b[i].l;
				maxr=minr=b[i].r;
			}
		}
	}
	return find(maxl)<=minr;
}
int main()
{
	int n,m,i,l=0,r,mid;
	cin>>n>>m;
	r=m;
	for(i=1;i<=m;i++)
	{
		cin>>a[i].l>>a[i].r>>a[i].x;
	}
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check(mid,n)==true)
		{
			l=mid+1;
		}
		else
		{
			r=mid-1;
		}
	}
	cout<<((r==m)?0:l)<<endl;//注意当没有矛盾时输出0
	return 0;
}